Masse manquante ?

Les différents problèmes de masse manquante sont résumés au
moyen du tableau classique suivant qui donne l'ordre de grandeur du
paramètre de densité Omega en fonction de l'échelle des
observations.
Omega-visible ~ 0.01 associée à la matière visible,
Omega-galaxie ~ 0.1 associée à la dynamique des galaxies,
Omega-amas ~ 0.2 à 0.3 associée à la dynamique
des amas,
Omega-lss ~ 0.8 +/- 0.5 associée aux grandes
structures.
Enfin beaucoup de cosmologistes voudraient (pour des raisons très diverses)
que Omega = Omega-univers soit exactement égal à 1!

Il n'est pas question de résoudre tout ces problèmes de masse manquante,
provenant des différences entre les "Omega observés", mais de
mieux les poser.
1- A l'échelle de l'univers le problème de la
détermination de Omega = Omega-univers en fonction de Ho et de
l'âge de l'univers, se pose de manière très différente suivant
les modèles, cf. la première
figure.
Dans le modèle standard,
pour que l'univers
soit plus âgé que les amas globulaires les plus vieux, il faut que non
seulement Ho soit plus petit que 60 km/s/Mpc, mais encore que Omega soit
petit, de fait Omega <= 0.1.
Dans le modèle de De Sitter par contre l'âge de l'univers augmente avec
Omega. En fait la seule contrainte que l'on ait pour que l'univers
soit plus âgé que les objets les plus vieux qu'il contient, est une borne
inférieure pour Omega en fonction de Ho; par exemple pour Ho=75,
il faut Omega >= 0.5.
2- Un gros problème classique de masse cachée
se manifeste au niveau des courbes
de rotation des galaxies (pour expliquer leur platitude). A la lumière de la
méthode que nous avons mise au point,
le phénomène de platitude des courbes
s'explique très simplement, sans recours à un éventuel halo massif, tout en
faisant apparaitre qu'il y a en fait moins de "masse cachée".
3- Pour estimer Omega-amas, il est usuel d'employer le classique
théorème du viriel qui permet d'évaluer la masse d'un amas à partir des
vitesses de dispersion des galaxies de cet amas. Mais ce théorème
du viriel est basé sur la loi d'attraction newtonienne, Il vaudrait
mieux utiliser un "théorème du viriel postnewtonien" et
comme le champ postnewtonien s'annulle au rayon d'attraction, la
correction risque fort d'être très importante. Plus
précisemment, les théories postnewtonienne et einsteinienne
étant équivalentes, il existe une pression gravitationnelle
pure (négative), d'où un concept de sphère (et de rayon)
d'attraction d'une condensation locale de matière dans un univers en
expansion. Ce fait a déjà été signalé par J.-M. Souriau.
Ainsi la relativité générale fournit, en utilisant cette notion
de sphère d'attraction, un nouveau moyen pour estimer
Omega-amas. Comme cette sphère d'attraction évolue avec
l'expansion et l'âge de l'amas considéré, on peut
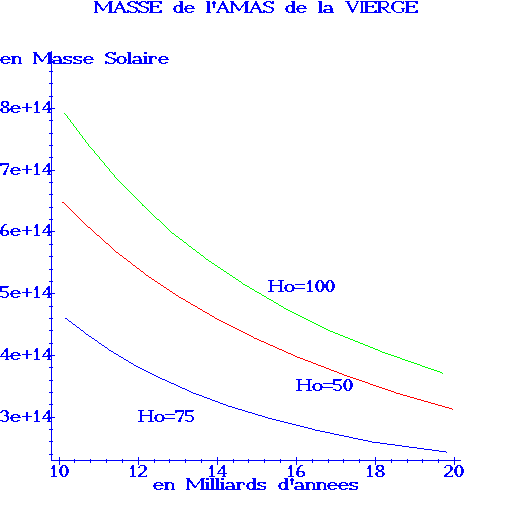
obtenir des estimations intéressantes. A titre d'illustration,
voici une estimation de la masse de l'amas de la Vierge en fonction de
son âge, pour différentes valeurs du paramètre de Hubble.