Des résultats "oubliés" en relativité générale
Painlevé et Gullstrand ont trouvé indépendamment en 1921 [1] une forme de métrique inhabituelle,
trop méconnue, qui rend compte du champ gravitationnel d'un astre dans l'univers
vide de Minkowski. La voici :
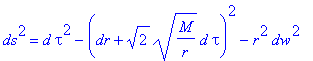
Extrêmement simple, on peut vérifier
facilement qu'elle est solution des équations d'Einstein dans le vide.
On peut l'obtenir très aisément à partir de la théorie de Newton de la gravitation :
Pourquoi ce résultat est-il oublié ? Cette question anodine (il y a tant de résultats oubliés)
est importante car cette métrique remet en cause la vision usuelle de la relativité générale.
En effet si l'on veut comprendre cette belle théorie d'Einstein, on ne peut pas faire l'économie
de la compréhension de cette métrique de Painlevé et Gullstrand.
Le principal intérêt réside dans son obtention rapide à partir de la gravitation
newtonienne :
on construit un lagrangien à partir de la vitesse radiale d'un corps en chute
libre de la forme :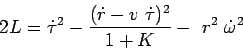 
où K est la constante du mouvement (i.e. la différence entre "l'énergie cinétique" et
"l'énergie potentielle" de la particule en chute libre considérée) puis on transforme ce
lagrangien en métrique, ce qui nous donne la forme de Painlevé-Gullstrand ci-dessus et plus
généralement :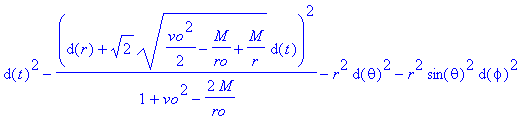 
Ce processus est en fait très général, pour le détail voir
ou comment passer de la théorie de Newton à celle (équivalente) d'Einstein.
Février 2011, une actualisation :
Forme de Painlevé d'une métrique à symétrie sphérique
Le petit problème se pose de retrouver la forme de métrique usuellement utilisée pour exprimer
le champ gravitationnel émis dans le vide; un simple changement de variable temporelle
nous donne :
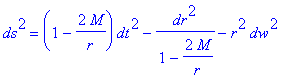QUELLE IMPOSTURE d'attribuer cette forme de métrique à Schwarzschild !
Relisez ses travaux, ils sont maintenant traduits en anglais :
Nous avons deux variables temporelles très différentes. La variable tau de la métrique
de Painlevé et Gullstrand indique le temps propre d'un corps en chute libre radiale,
autrement dit c'est le temps indiqué par l'horloge transportée par ce corps.
Mais qu'est-ce temps t de la métrique faussement attribuée à Karl Schwarzschild ?
Qui a mis sur le marché cette forme de métrique, qui, mal comprise, entraine des erreurs
grossières (en particulier cette histoire de singularité qui n'existe pas pour la forme
de Painlevé et Gullstrand) ?
On pourra voir par exemple le travail de
S. Antoci.
Cette erreur de Hilbert et d'autres a eu de nombreuses conséquences, en particulier l'oubli
de cette splendide forme de Painlevé et en second lieu une avalanche de travaux conduisant
à la déraisonable étude du concept de trous noirs, concept
n'ayant aucun sens physique comme
le disait Einstein lui-même dans un article de 1939.
Mais qui a lu cet article d'Einstein ?
[1] P. Painlevé, La mécanique classique et la théorie de la relativité,
C. R. Acad. Sci. (Paris), 173, pp. 677-680 (1921).
A. Gullstrand, Allegemeine lösung des statischen einkörper-problems in der
Einsteinshen gravitations theorie,
Arkiv. Mat. Astron. Fys. 16(8), pp. 1-15 (1922).
retour 
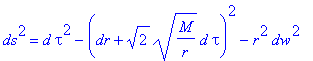
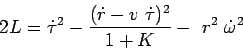
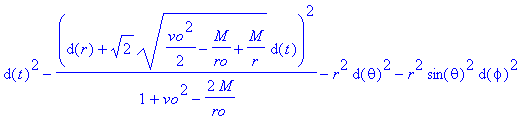
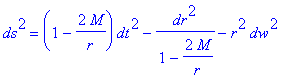
A lire aussi.