Classification des projections
On peut classer les projections selon les propriétés géométriques
des parallèles et des méridiens (survivance des vieilles constructions géométriques...).
Il est évident que les propriétés d'une projection sont conservées par un
changement de repère initial sur la sphère, qui change le centre de
projection. Les propriétés des parallèles et méridiens citées par la
suite s'appliquent donc aux lignes ''fictives'' passant par le point
central choisi selon une direction donnée. Ces lignes, si le point
central n'est pas sur l'équateur ou que la direction choisie n'est pas
celle des lignes physiques de la Terre, diffèrent de celles que l'on
désigne conventionnellement par ces noms.
Une projection est dite :
- méricylindrique lorsque le méridien central est une
droite (ou un segment), les parallèles des droites (ou des segments voire
des points) perpendiculaires au méridien central, et les méridiens des
courbes coupant les parallèles à intervalles réguliers ;
- cylindrique lorsqu'elle est méricylindrique et les
méridiens sont des droites parallèles entre elles ;
- polyconique lorsque le méridien central est une droite, les
parallèles des arcs de cercles dont les centres sont sur le méridien
central et les méridiens des courbes coupant les parallèles à intervalles réguliers ;
- mériconique lorsqu'elle est polyconique et les
parallèles sont concentriques ;
- tronconique lorsqu'elle est mériconique et les
méridiens sont des droites se coupant au centre des parallèles ;
- conique lorsqu'elle est tronconique et un pôle
est ponctuel (dans toute la suite, par ''le pôle'' on entendra le point
de latitude
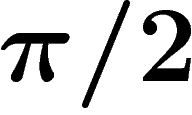 ) ;
) ;
- azimutale (ou zénithale) lorsqu'elle
est conique et les parallèles sont des cercles complets. (C'est terminé!)
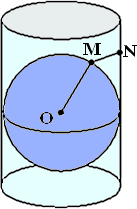
Les projections cylindriques
On voit qu'une projection cylindrique s'apparente à une projection
géométrique de la sphère sur un cylindre tangent à l'équateur qui est
ensuite développé :
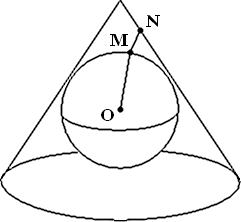
Les projections coniques
Une projection conique ou tronconique est comparable à une projection sur
un cône dont l'axe passe par les pôles :
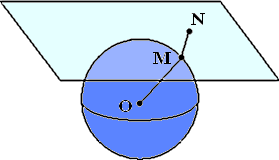
Les projections azimutales
Une projection azimutale peut être rapprochée d'une projection sur un
plan tangent au pôle (vue de dessous) :
Les projections perspectives
Une projection obtenue par une véritable projection géométrique de la
sphère à partir d'un centre sur une surface quelconque qui sera ensuite
développée est dite perspective.
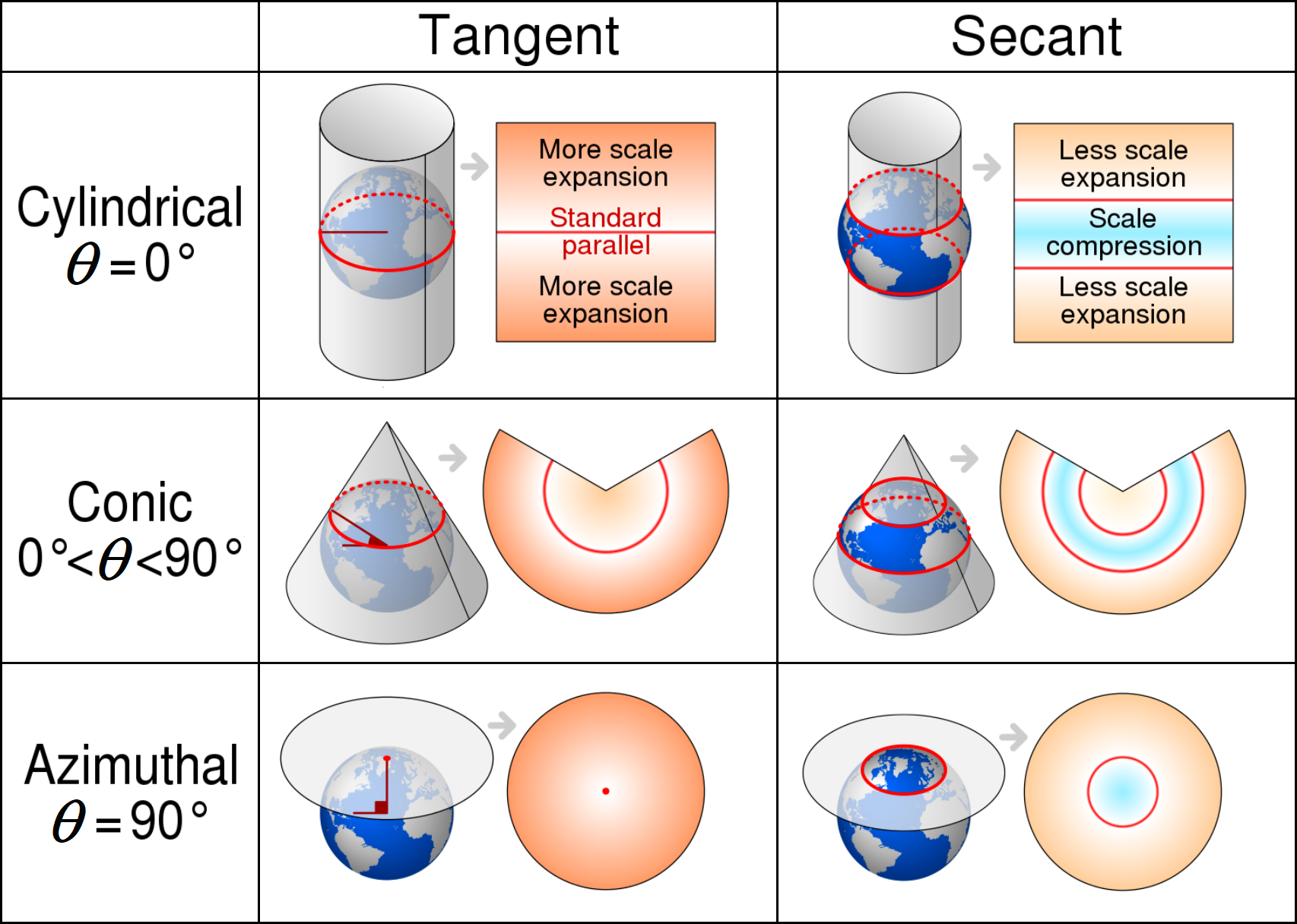
Récapitulatif des projections
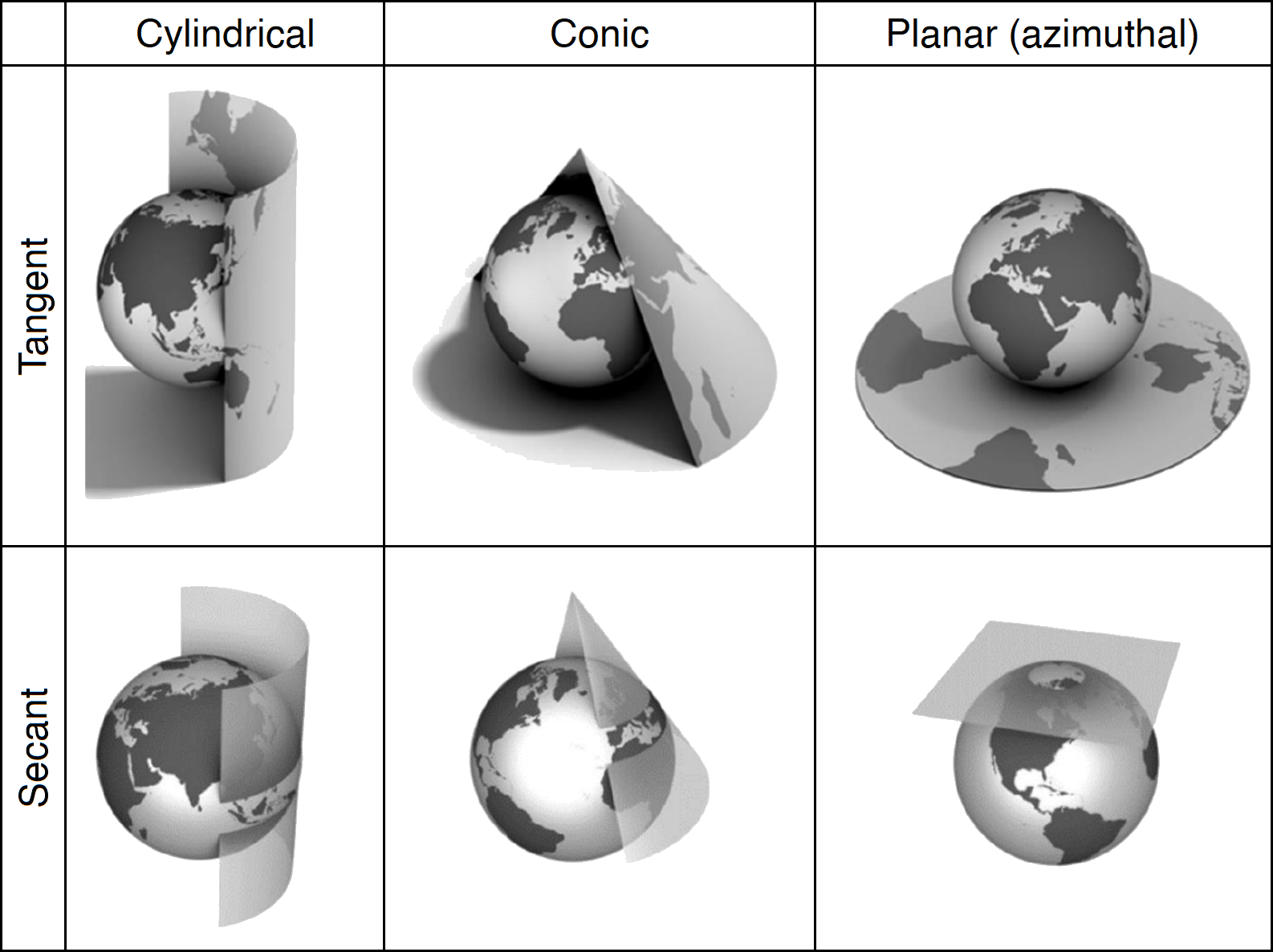
Comparaison des déformations
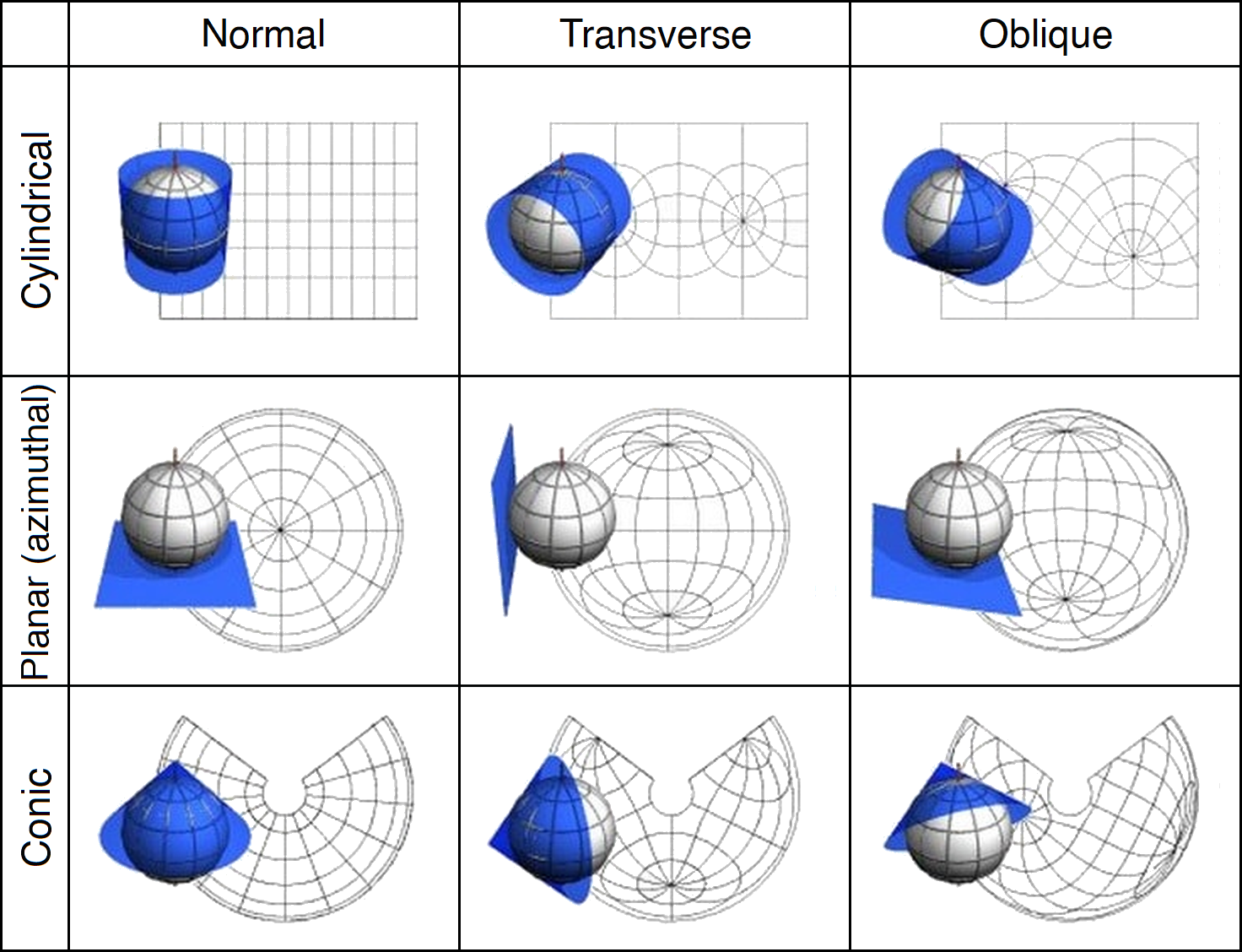
Aspect transverse/oblique
À propos des changements de repère : une projection A est dite être
l'aspect transverse d'une autre projection B si les parallèles
et méridiens fictifs construits de telle sorte que l'équateur fictif soit
sur un méridien physique donnent par A la même image (à isométrie près
bien entendu) que les lignes physiques par B. La projection B, par
comparaison, est dite directe. A et B ont ainsi les mêmes
équations si on effectue préalablement un changement de repère. Plus
généralement, si pour A un changement de repère quelconque redonne le
même réseau de méridiens et parallèles que pour B, A est dit être
l'aspect oblique de B. On ne considérera ici, sauf mention contraire,
que l'aspect direct.
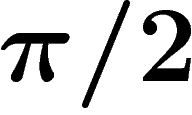 ) ;
) ;
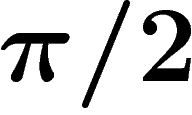 ) ;
) ;