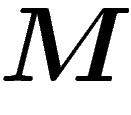 le point de la sphère (de rayon pris égal à
le point de la sphère (de rayon pris égal à 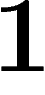 )
de longitude
)
de longitude  et de latitude
et de latitude  ,
,
 son projeté sur la carte de coordonnées
cartésiennes
son projeté sur la carte de coordonnées
cartésiennes 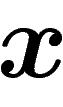 et
et 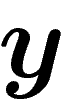 dans un repère orthonormé, avec en coordonnées polaires
dans un repère orthonormé, avec en coordonnées polaires
 et
et  :
:
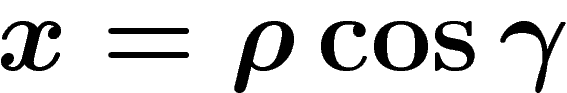 et
et 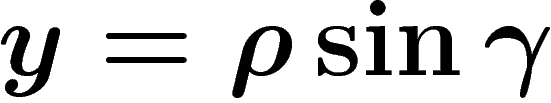 .
.
Les projections sont surtout classées selon les propriétés qu'elles conservent (pour les optimistes) ou le type de déformations qu'elles induisent (pour les pessimistes) :
Les projections
Les autres projections sont dites aphylactiques.
Hors de cette classification, une projection azimutale conserve les angles dont le sommet est le centre de la projection (les azimuts) et les projections orthodromiques conservent les géodésiques (voir la conclusion de cet article).
Il existe des conditions simples pour juger de l'équivalence ou de la
conformité d'une projection. On notera
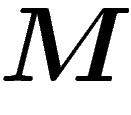 le point de la sphère (de rayon pris égal à
le point de la sphère (de rayon pris égal à 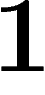 )
de longitude
)
de longitude  et de latitude
et de latitude  ,
,
 son projeté sur la carte de coordonnées
cartésiennes
son projeté sur la carte de coordonnées
cartésiennes 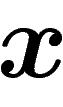 et
et 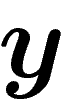 dans un repère orthonormé, avec en coordonnées polaires
dans un repère orthonormé, avec en coordonnées polaires
 et
et  :
:
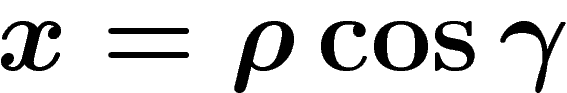 et
et 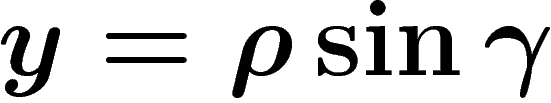 .
.
L'aire d'un petit élément de surface de la sphère, d'étendue
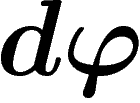 en
longitude et
en
longitude et 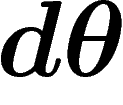 en latitude, est
en latitude, est
![\[
d\phi\,d\theta \cos \theta\]](carto013.png)
L'aire orientée de l'élément correspondant sur la carte est
![\[
\begin{array}{|cc|}
\frac{\partial x}{\partial \phi}&\frac{\partial y}{\partial \phi}\\
\frac{\partial x}{\partial \theta}&\frac{\partial y}{\partial \theta}
\end{array}
\,\,d\phi \,d\theta=\left(\frac{\partial x}{\partial \phi}\frac{\partial y}{\partial \theta}
-\frac{\partial x}{\partial \theta}\frac{\partial y}{\partial \phi}\right)\,d\phi \,d\theta
\]](carto014.png)
Si cette quantité est positive, on obtient une image directe de la région
considérée, sinon on obtient une image retournée. L'échelle locale, pour
les aires, d'une projection est donc définie comme étant le rapport des deux coefficients devant
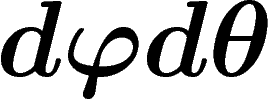
![\[
\frac{1}{\cos \theta}\left(\frac{\partial x}{\partial \phi}\frac{\partial y}{\partial \theta}
-\frac{\partial x}{\partial \theta}\frac{\partial y}{\partial \phi}\right)
\]](carto015.png)
(si le second terme est non nul au pôle, cette quantité y est infinie).
Pour une projection équivalente, la quantité ci-dessus vaut
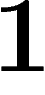 ,
on en déduit :
,
on en déduit :
![\[
\frac{\partial x}{\partial \phi}\frac{\partial y}{\partial \theta}
-\frac{\partial x}{\partial \theta}\frac{\partial y}{\partial \phi}
=\cos \theta\]](carto016.png)
![\[
\rho\left(\frac{\partial \rho}{\partial \phi}\frac{\partial \gamma}{\partial \theta}
-\frac{\partial \rho}{\partial \theta}\frac{\partial \gamma}{\partial \phi}\right)=\cos \theta
\]](carto017.png)
De la même manière, on définit l'échelle locale sur les méridiens par
![\[
\sqrt{\left(\frac{\partial x}{\partial \theta}\right)^2
+\left(\frac{\partial y}{\partial \theta}\right)^2}
=\sqrt{\left(\frac{\partial \rho}{\partial \theta}\right)^2
+\rho^2\left(\frac{\partial \gamma}{\partial \theta}\right)^2}
\]](carto018.png)
![\[
\frac{1}{\cos \theta}\sqrt{\left(\frac{\partial x}{\partial \phi}\right)^2
+\left(\frac{\partial y}{\partial \phi}\right)^2}
=\frac{1}{\cos \theta}\sqrt{\left(\frac{\partial \rho}{\partial \phi}\right)^2
+\rho^2\left(\frac{\partial \gamma}{\partial \phi}\right)^2}
\]](carto019.png)
Cette fois-ci on ne peut distinguer une image retournée : à laquelle des deux échelles attribuer un signe négatif ?
Une projection sera conforme lorsqu'elle est localement
assimilable à une similitude, autrement dit si le quadrilatère
représentant un petit rectangle
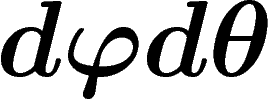 de la sphère est lui-même un rectangle et que les échelles des méridiens et des parallèles sont
localement égales. On en déduit :
de la sphère est lui-même un rectangle et que les échelles des méridiens et des parallèles sont
localement égales. On en déduit :
![\[
\left\{\begin{array}{ll}\displaystyle
\frac{\partial x}{\partial \phi}\frac{\partial x}{\partial \theta}+
\frac{\partial y}{\partial \phi}\frac{\partial y}{\partial \theta}=0\\
\null\\
\displaystyle\left(\frac{\partial x}{\partial \phi}\right)^2+\left(\frac{\partial y}{\partial \phi}\right)^2
=\cos^2 \theta\left(
\left(\frac{\partial x}{\partial \theta}\right)^2+\left(\frac{\partial y}{\partial \theta}\right)^2
\right)\end{array}\right.\]](carto021.png)
Pour avoir ceci en coordonnées polaires, il suffit de remplacer les
termes en 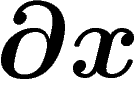 par
par 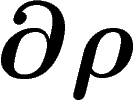 et ceux en
et ceux en 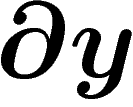 par
par
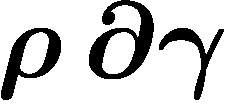 .
.
Si on note 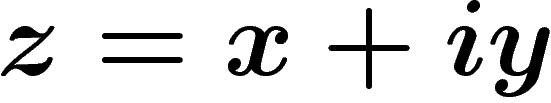 ,
et si
,
et si 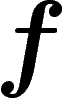 est une application holomorphe et
est une application holomorphe et
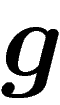 une projection conforme telle que
une projection conforme telle que
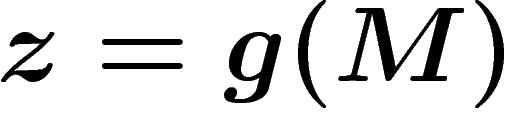 ,
la projection
,
la projection  est elle aussi conforme puisque
est elle aussi conforme puisque
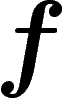 est assimilable localement à une similitude.
Réciproquement, si deux projections injectives sont conformes, il existe
nécessairement (si on tient aussi compte des points à l'infini) une
application holomorphe transformant l'une en l'autre, car la fonction
transformant l'une en l'autre doit elle aussi être assimilable localement
à une similitude. Ainsi on peut obtenir toutes les projections injectives
conformes à partir d'une seule par composition par des fonctions
holomorphes.
est assimilable localement à une similitude.
Réciproquement, si deux projections injectives sont conformes, il existe
nécessairement (si on tient aussi compte des points à l'infini) une
application holomorphe transformant l'une en l'autre, car la fonction
transformant l'une en l'autre doit elle aussi être assimilable localement
à une similitude. Ainsi on peut obtenir toutes les projections injectives
conformes à partir d'une seule par composition par des fonctions
holomorphes.
Enfin, pour les projections équidistantes, l'échelle sur les méridiens vaut
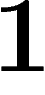 , ce qui donne :
, ce qui donne :
![\[
\left(\frac{\partial x}{\partial \theta}\right)^2
+\left(\frac{\partial y}{\partial \theta}\right)^2=1
\]](carto029.png)
On peut appliquer ces résultats pour retrouver les projections couramment utilisées. On étudiera dans chaque catégorie principale (cylindrique, azimutale, tronconique) les projections perspectives, équidistantes, équivalentes, conformes.

| Les projections cylindriques |