 ,
,
 ),
les projections azimutales sont de la forme
),
les projections azimutales sont de la forme
En coordonnées polaires
( ,
,
 ),
les projections azimutales sont de la forme
),
les projections azimutales sont de la forme
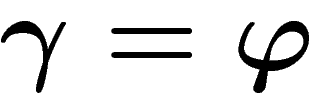 et
et
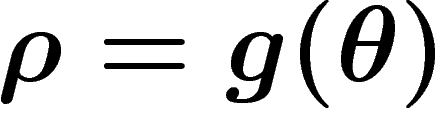
|
avec 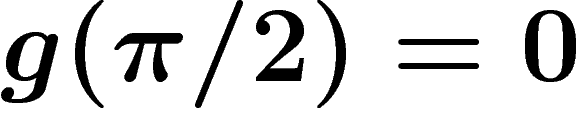 ,
ou encore, en posant
,
ou encore, en posant
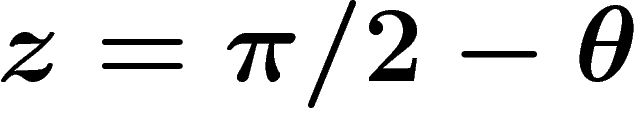 (
( est la colatitude de
est la colatitude de
 et simplifie les calculs) :
et simplifie les calculs) :
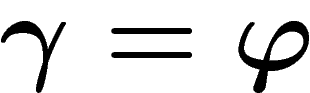 et
et
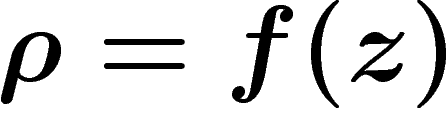
|
avec 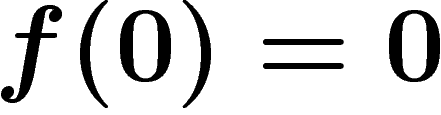 .
.
La condition ![\[
\rho\left(\frac{\partial \rho}{\partial \phi}\frac{\partial \gamma}{\partial \theta}
-\frac{\partial \rho}{\partial \theta}\frac{\partial \gamma}{\partial \phi}\right)=\cos \theta
\]](carto017bis.png) s'écrit
s'écrit 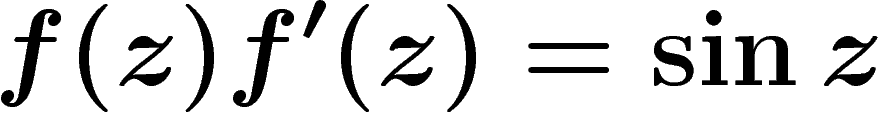 .
.
Les conditions ![\[
\left\{\begin{array}{ll}\displaystyle
\frac{\partial \rho}{\partial \phi}\frac{\partial \rho}{\partial \theta}+\rho^2\frac{\partial \gamma}{\partial \phi}\frac{\partial \gamma}{\partial \theta}=0\\
\null\\
\displaystyle\left(\frac{\partial \rho}{\partial \phi}\right)^2+\left(\frac{\partial \gamma}{\partial \phi}\right)^2
=\cos^2 \theta\left(\left(\frac{\partial \rho}{\partial \theta}\right)^2+\rho^2\left(\frac{\partial \gamma}{\partial \theta}\right)^2
\right)\end{array}\right.\]](carto021ter.png) s'écrivent simplement
s'écrivent simplement ![\[f(z)^2=\sin^2z\,f'(z)^2\]](carto079.png) .
.
La condition ![\[
\left(\frac{\partial \rho}{\partial \theta}\right)^2+\rho^2 \left(\frac{\partial \gamma}{\partial \theta}\right)^2=1
\]](carto029ter.png) s'écrit
s'écrit 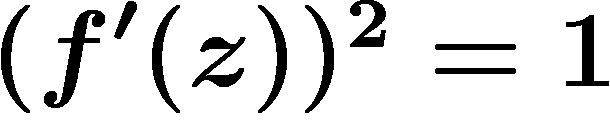 .
.
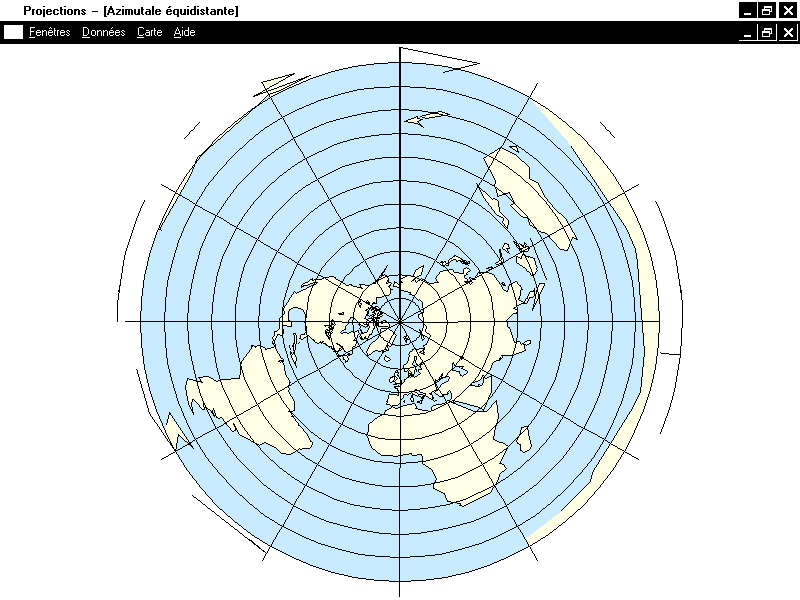
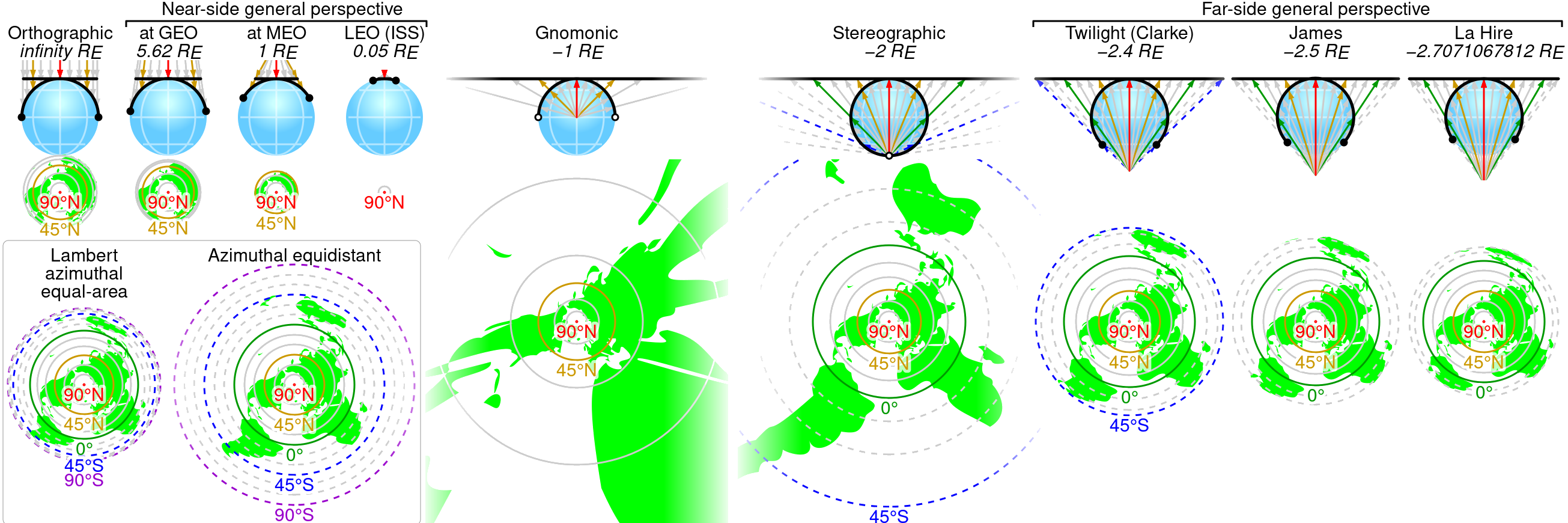
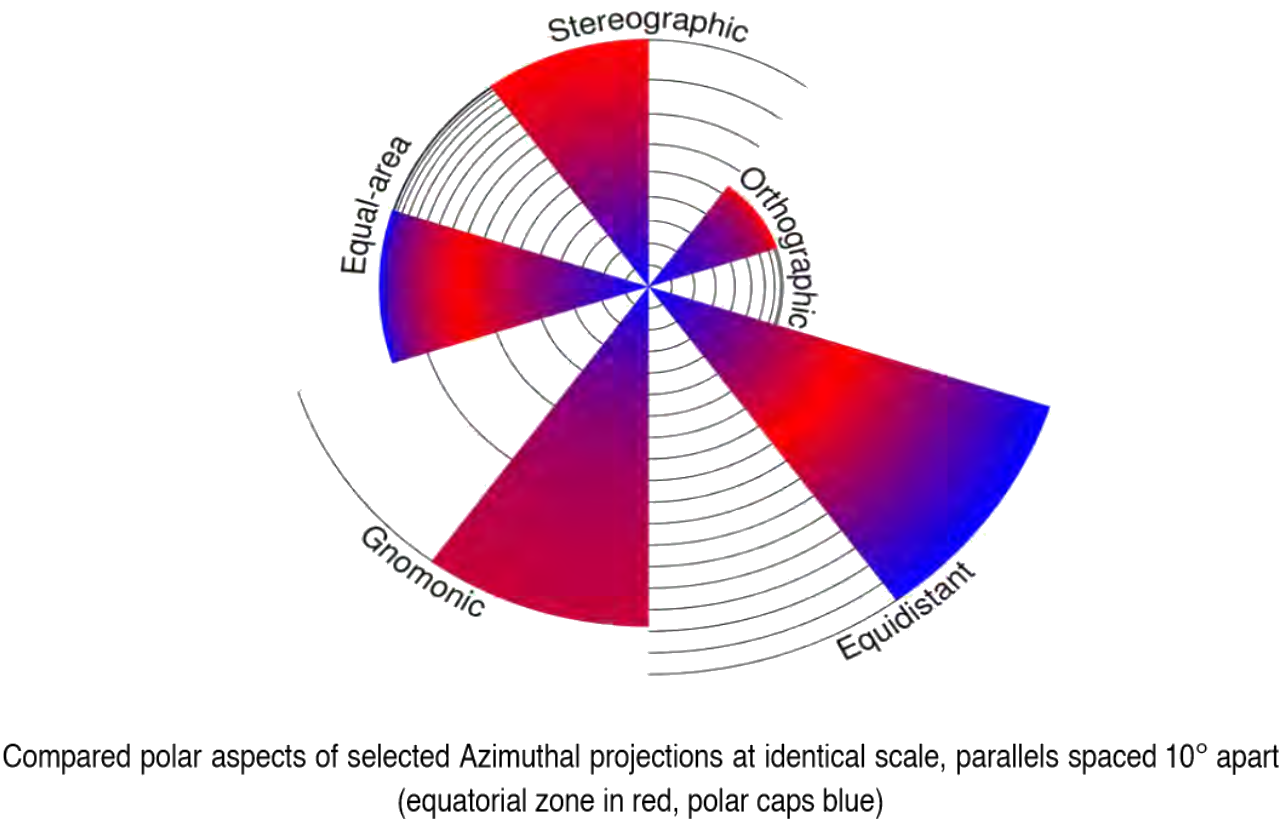
Il existe une infinité de projections azimutales perspectives (comme de
projections cylindriques perspectives). On n'étudiera donc que deux cas :
le point de vue est soit au centre de la sphère, soit à l'infini. Pour
les mêmes raisons que pour les projections cylindriques on considérera
uniquement des projections sur un plan tangent, de manière à ne pas avoir
de déformation au voisinage du point central
(donc 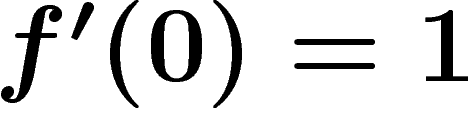 ).
).
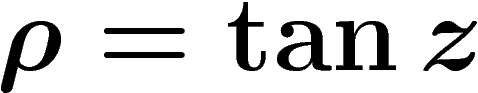 ,
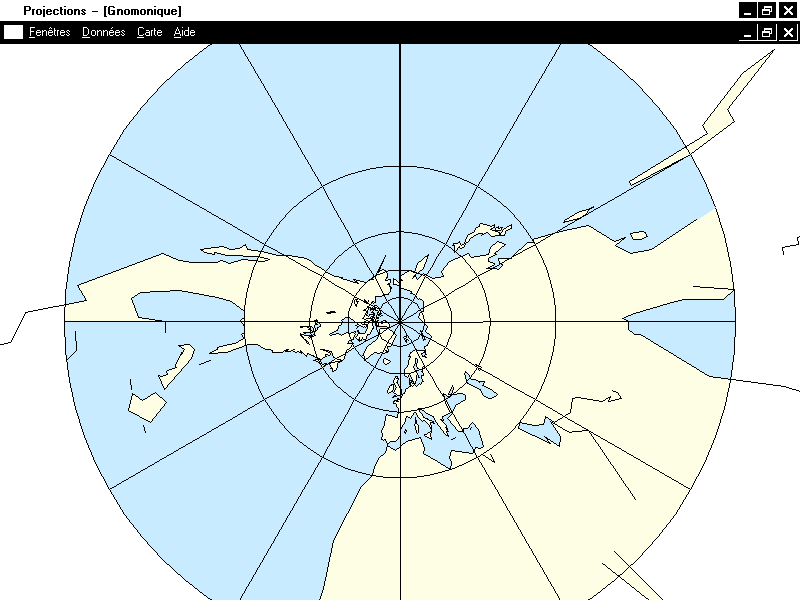
on obtient la projection gnomonique (ou centrale). Elle est donnée par
,
on obtient la projection gnomonique (ou centrale). Elle est donnée par
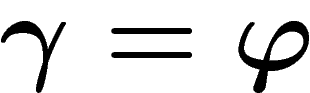 et
et
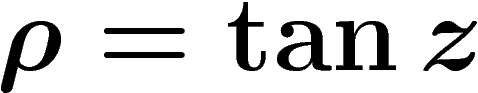
|

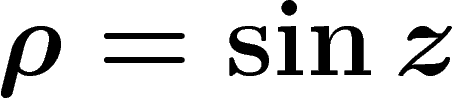 ,
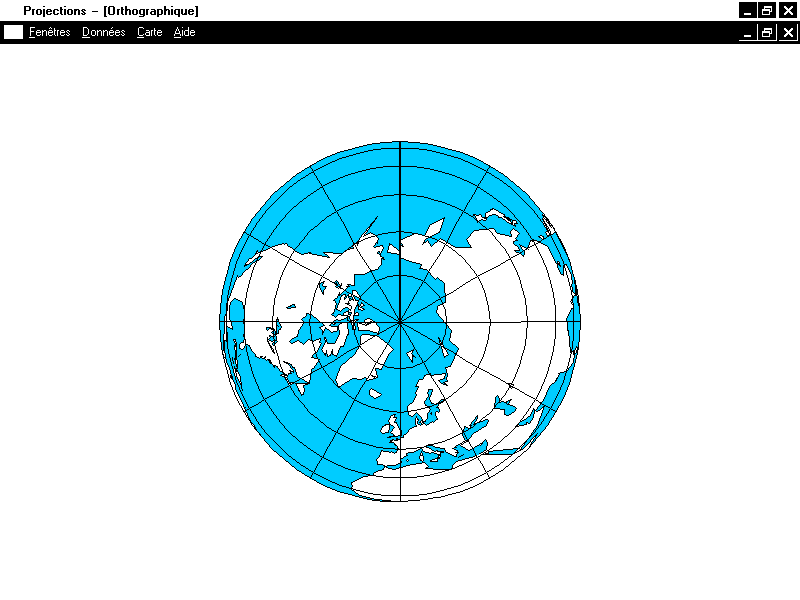
on obtient une projection orthogonale, appelée projection orthographique,
donnée par
,
on obtient une projection orthogonale, appelée projection orthographique,
donnée par
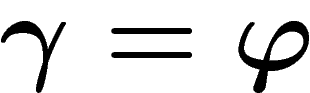 et
et
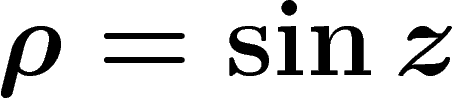
|

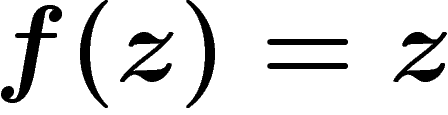 (au signe près, qui n'est qu'une rotation), soit
(au signe près, qui n'est qu'une rotation), soit
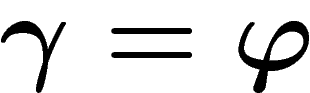 et
et
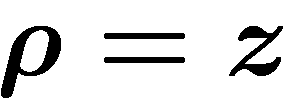
|

![\[f(z)f'(z)=\sin z\]](carto077.png) d'où (avec la condition
d'où (avec la condition 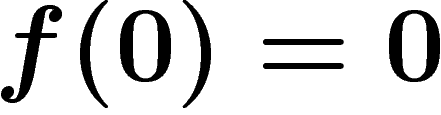 , au signe près)
, au signe près)
 , soit
, soit
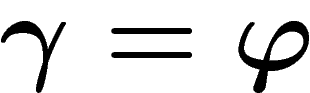 et
et
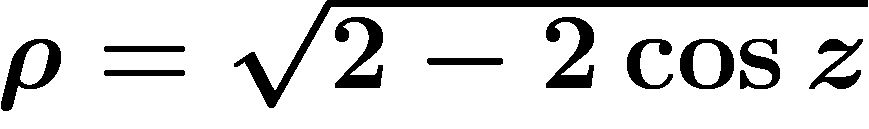
|
 .
.

![\[f(z)^2=\sin^2z\,f'(z)^2\]](carto079.png) d'où l'on tire (avec la condition
d'où l'on tire (avec la condition 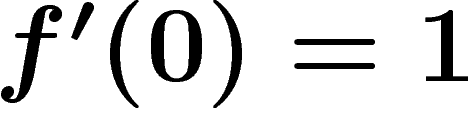 , au signe près)
, au signe près)
![\[f(z)=2\tan z/2\]](carto080.png) ,
,
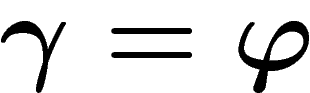 et
et
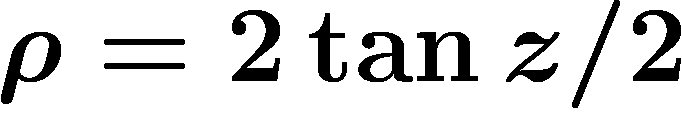
|
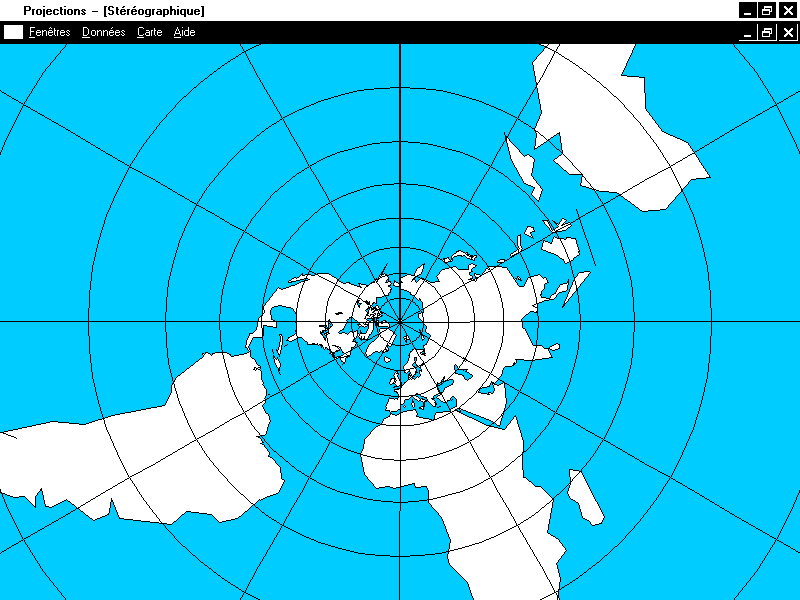

On peut trouver une relation dans le plan complexe entre la projection
stéréographique et la projection de Mercator. En effet, rappelons que
![\[
\pounds= \log\left(\tan\left(\frac{\theta}{2}+\frac{\pi}{4}\right)\right)
= -\log\left(\tan\left(\frac{z}{2}\right)\right)
\]](carto046ter.png) . On a alors (au coefficient multiplicatif 2 près)
. On a alors (au coefficient multiplicatif 2 près)
![\[
\text{stéréographique}=e^{i\text{Mercator}}=e^{i\phi-\pounds}\]](carto081.png)
|
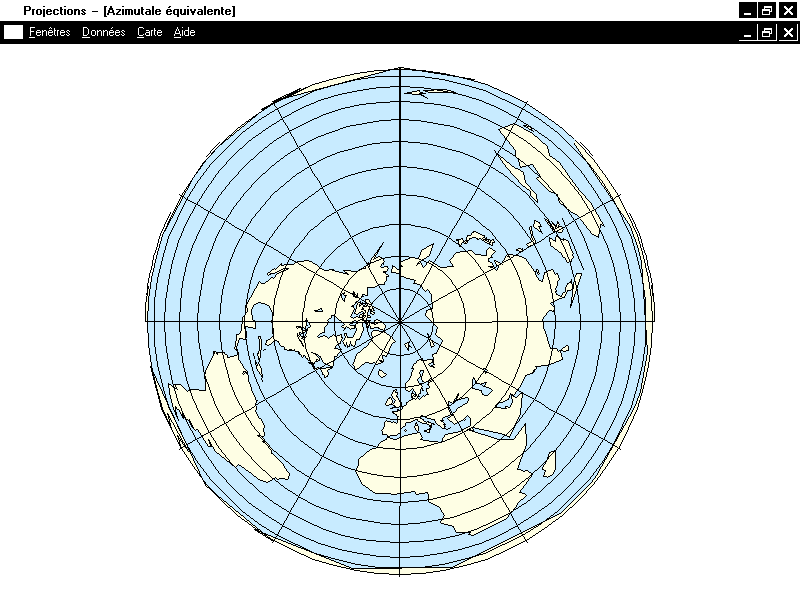
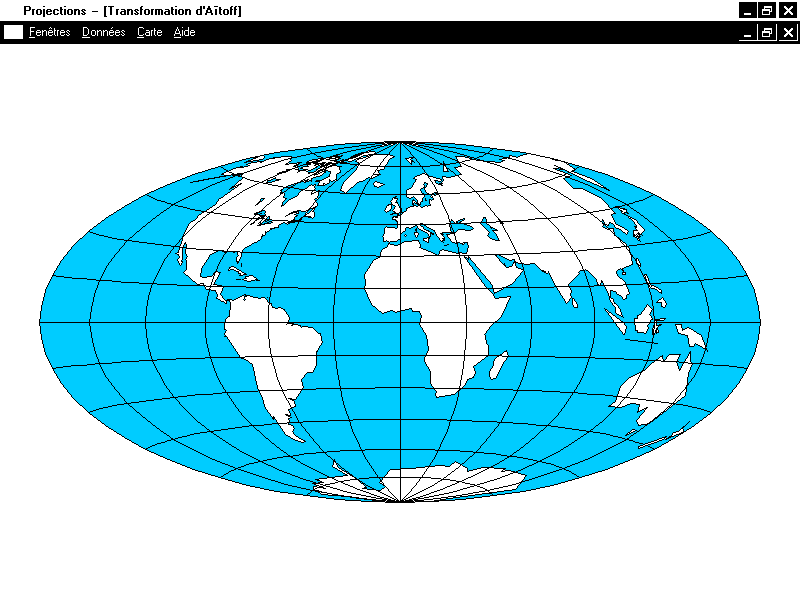
Signalons enfin une transformation couramment utilisée pour les projections azimutales. La transformation d'Aïtoff-Hammer (Aïtoff l'a inventée pour la projection de G. Postel et Hammer n'a fait que l'appliquer telle quelle à d'autres projections). Elle se base sur l'aspect transverse de ces dernières (ce qui change totalement les aspects des parallèles et méridiens) et consiste à diviser les longitudes par un nombre supérieur à 1 (2 en général), à appliquer la projection transverse à la surface partielle de sphère ainsi obtenue, et à remultiplier les abscisses par ce nombre. De manière intéressante, cette transformation conserve la propriété d'équivalence.

| Les projections (tron)coniques |