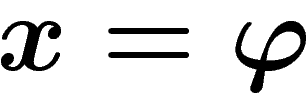 et
et
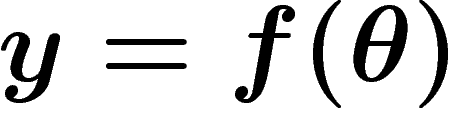
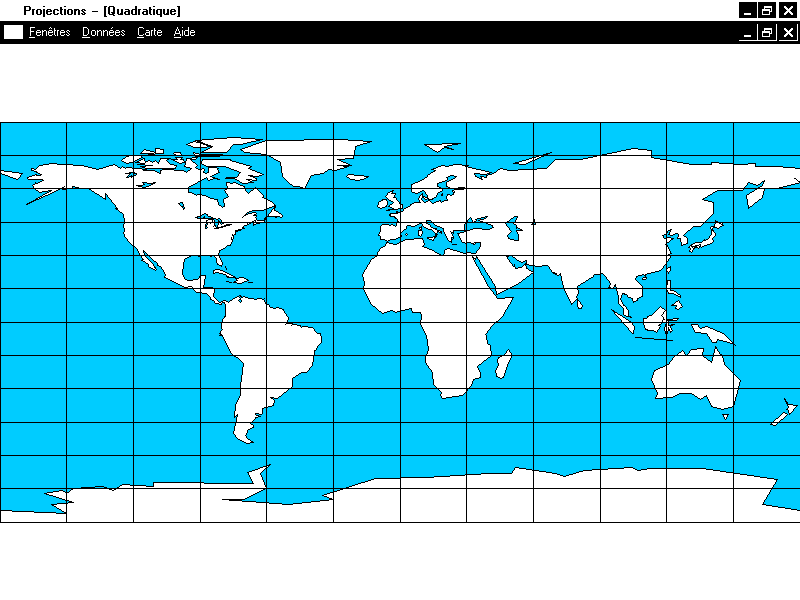
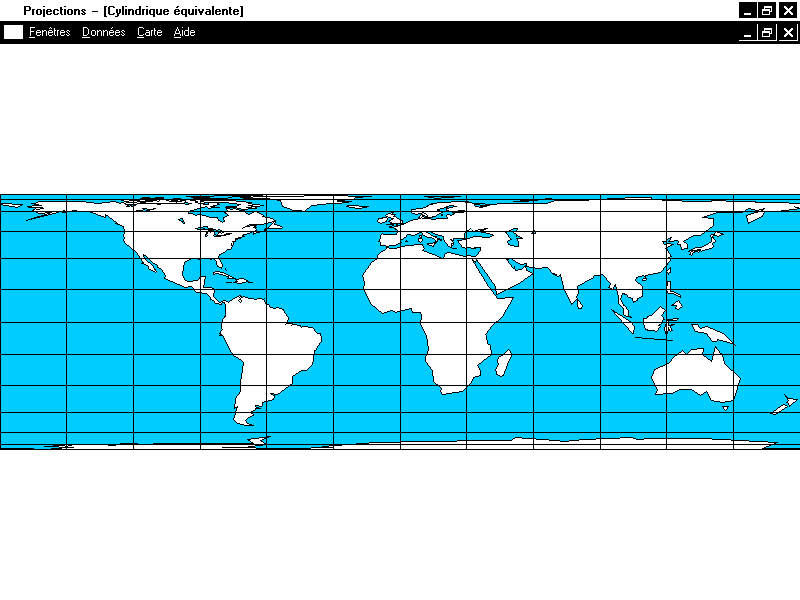
Pour les projections cylindriques, on considérera un cylindre tangent à l'équateur, un cylindre sécant ou extérieur n'introduisant qu'un facteur d'échelle. En coordonnées cartésiennes, les projections cylindriques sont, dans un repère convenable, de la forme
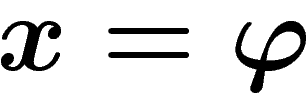 et
et
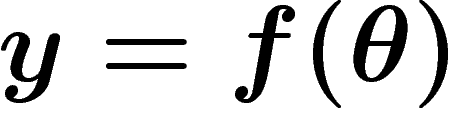
|
avec 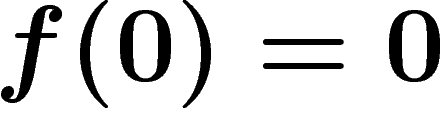 .
Réécrivons les conditions 1,2,3 dans ce contexte.
.
Réécrivons les conditions 1,2,3 dans ce contexte.
La condition ![\[
\frac{\partial x}{\partial \phi}\frac{\partial y}{\partial \theta}-\frac{\partial x}{\partial \theta}\frac{\partial y}{\partial \phi}
=\cos \theta\]](carto016bis.png) s'écrit
s'écrit 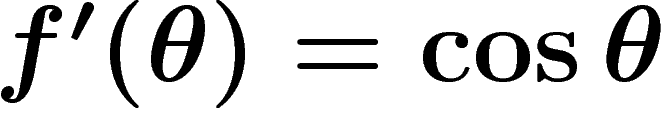 .
.
Les conditions ![\[
\left\{\begin{array}{ll}\displaystyle
\frac{\partial x}{\partial \phi}\frac{\partial x}{\partial \theta}+\frac{\partial y}{\partial \phi}\frac{\partial y}{\partial \theta}=0\\
\null\\
\displaystyle\left(\frac{\partial x}{\partial \phi}\right)^2+\left(\frac{\partial y}{\partial \phi}\right)^2
=\cos^2 \theta\left(\left(\frac{\partial x}{\partial \theta}\right)^2+\left(\frac{\partial y}{\partial \theta}\right)^2
\right)\end{array}\right.\]](carto021bis.png) s'écrivent simplement
s'écrivent simplement 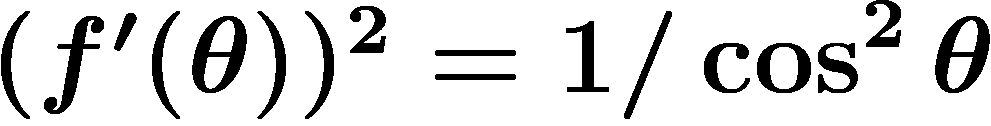 .
.
La condition ![\[
\left(\frac{\partial x}{\partial \theta}\right)^2+\left(\frac{\partial y}{\partial \theta}\right)^2=1
\]](carto029bis.png) s'écrit
s'écrit 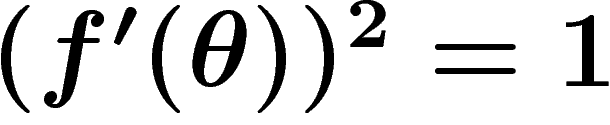 .
.
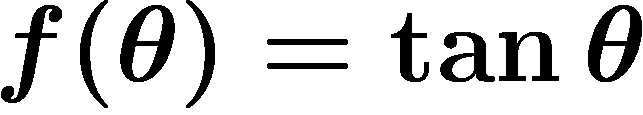 ,
et donc
,
et donc
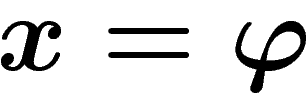 et
et
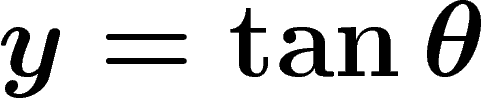
|
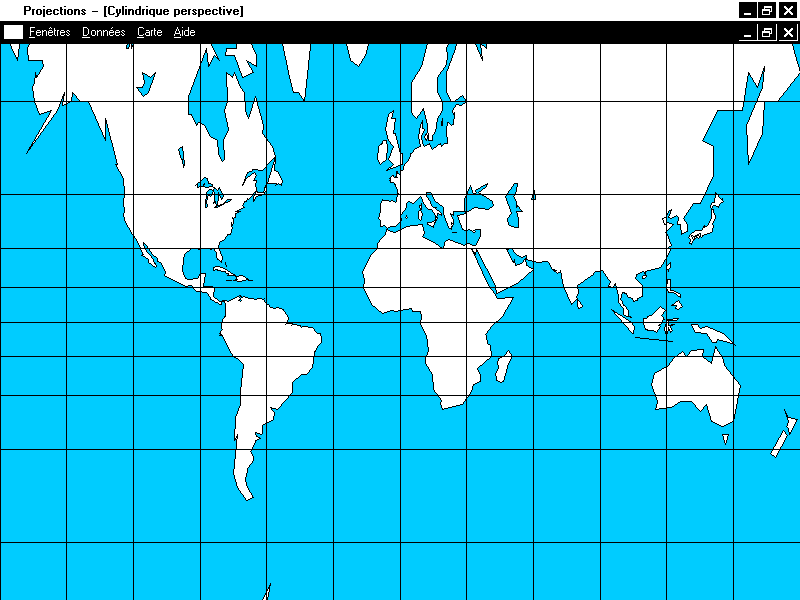
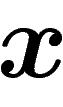 et
et 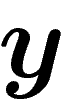 doivent vérifier la condition 3 qui s'écrit alors
doivent vérifier la condition 3 qui s'écrit alors
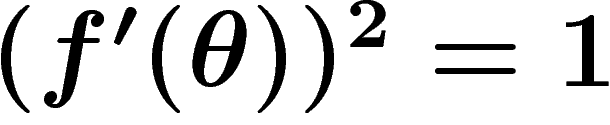 ,
soit, puisque
,
soit, puisque
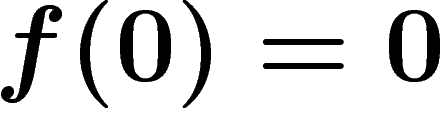 ,
,
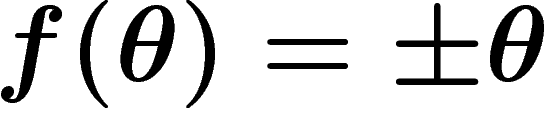 .
Pour avoir une carte non retournée, on prend bien sûr
.
Pour avoir une carte non retournée, on prend bien sûr
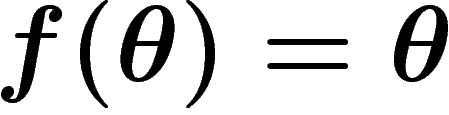 pour avoir une échelle des aires positive.
Finalement
pour avoir une échelle des aires positive.
Finalement
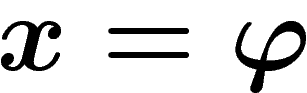 et
et
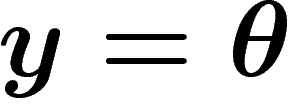
|

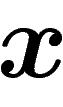 et
et 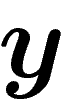 doivent vérifier la condition 1 qui s'écrit alors
doivent vérifier la condition 1 qui s'écrit alors
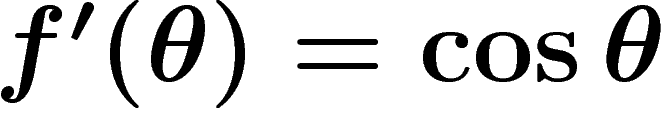 ,
d'où
,
d'où 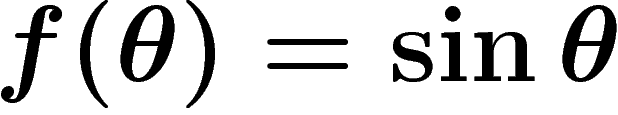 .
On obtient donc
.
On obtient donc
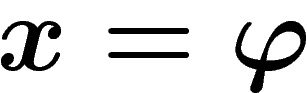 et
et
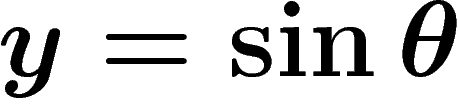
|

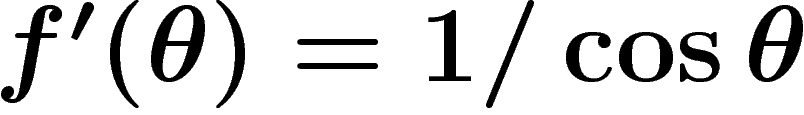 .
On vérifie que
.
On vérifie que
![\[
\pounds=f(\theta) = \log\left(\tan\left(\frac{\theta}{2}+\frac{\pi}{4}\right)\right)
=2\,\mathrm{argtanh}\left(\tan\left(\frac{\theta}{2}\right)\right)
=2\,\mathrm{argsinh}\big(\tan(\theta)\big)\]](carto046.png)
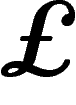 .
On a donc
.
On a donc
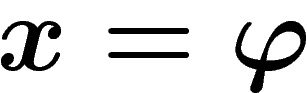 et
et

|
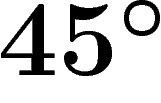 l'échelle des aires est déjà
l'échelle des aires est déjà
 .
.
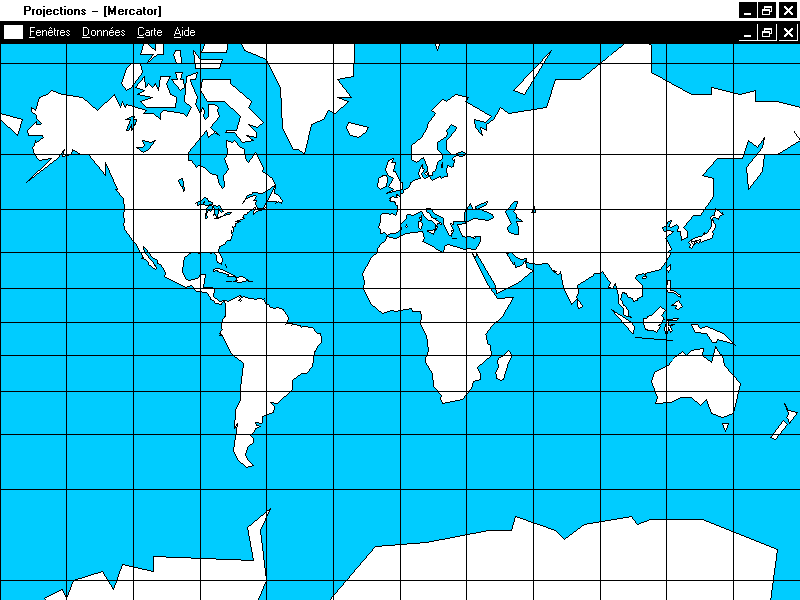

Un parallèle plus égal que les autres. Dans ce qui précède,
on a toujours supposé que l'échelle était conservée sur l'équateur. On
peut, par une application affine, rendre un autre parallèle de vraie
longueur et même le rendre automécoïque, c'est-à-dire supprimer toute
déformation à son niveau, de manière à conserver les autres propriétés de
la projection (équidistance, équivalence, conformité). Ceci signifie que
la carte est conforme le long de ce parallèle et que les deux échelles
locales selon les parallèles et les méridiens valent
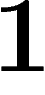 .
.
Si la projection cylindrique s'écrit
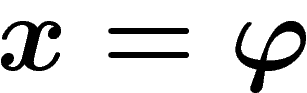 et
et 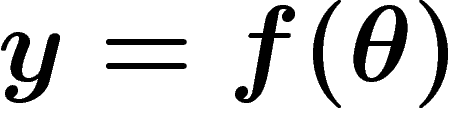 ,
et si l'on veut conserver le parallèle de latitude
,
et si l'on veut conserver le parallèle de latitude
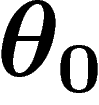 ,
il suffit de prendre
,
il suffit de prendre
![\[x_2=\phi \cos \theta_0\]](carto053.png) et
et
![\[y_2=f(\theta)/f'(\theta_0)\]](carto054.png)
|
La projection quadratique devient ainsi la projection ''des cartes plates parallélogrammatiques''. Pour la projection de Mercator, ceci est une simple homothétie (cette projection étant déjà conforme partout).
À partir de la projection cylindrique de Lambert, on peut obtenir, en
particulier, la fameuse projection de Peters, dont il convient de
dénoncer l'hypocrisie : elle se présente en alternative de la projection
de Mercator, dans laquelle les pays en voie de développement, de faible
latitude, sont plus petits que les autres ; la projection de Peters,
elle, conserve bien les surfaces, mais on a choisi
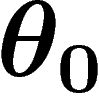 de manière à ne pas déformer les pays développés,
ce qui a pour conséquence, naturellement, de déformer considérablement
les P.V.D., et ceci est souvent présenté comme une fatalité, le prix à
payer pour obtenir l'équivalence !
de manière à ne pas déformer les pays développés,
ce qui a pour conséquence, naturellement, de déformer considérablement
les P.V.D., et ceci est souvent présenté comme une fatalité, le prix à
payer pour obtenir l'équivalence !
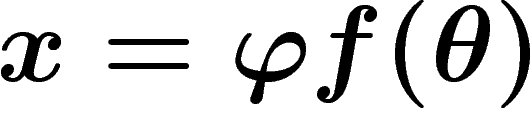 et
et
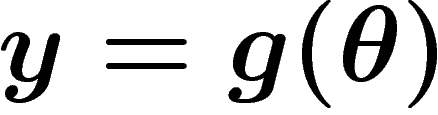 avec
avec 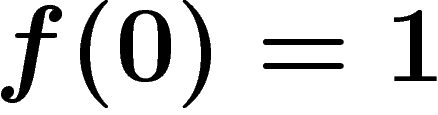 ,
,
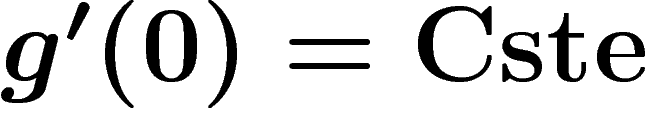 et
et 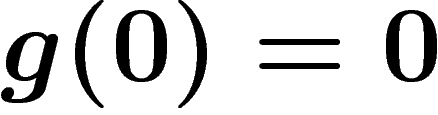 .
On doit, en tout point, avoir
.
On doit, en tout point, avoir
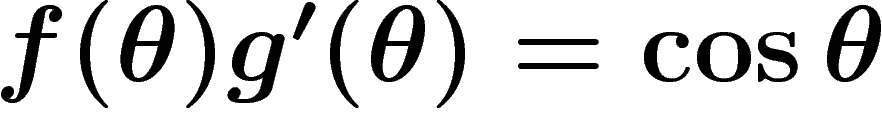 ,
d'où une famille de projections
,
d'où une famille de projections
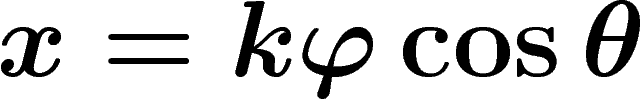 et
et
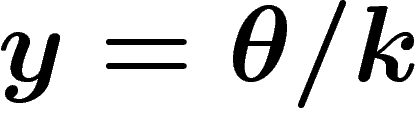
|
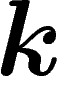 , et l'échelle sur le méridien central
, et l'échelle sur le méridien central
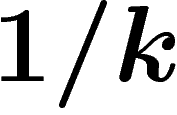 ,
ce qui incite à prendre
,
ce qui incite à prendre 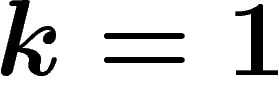 ,
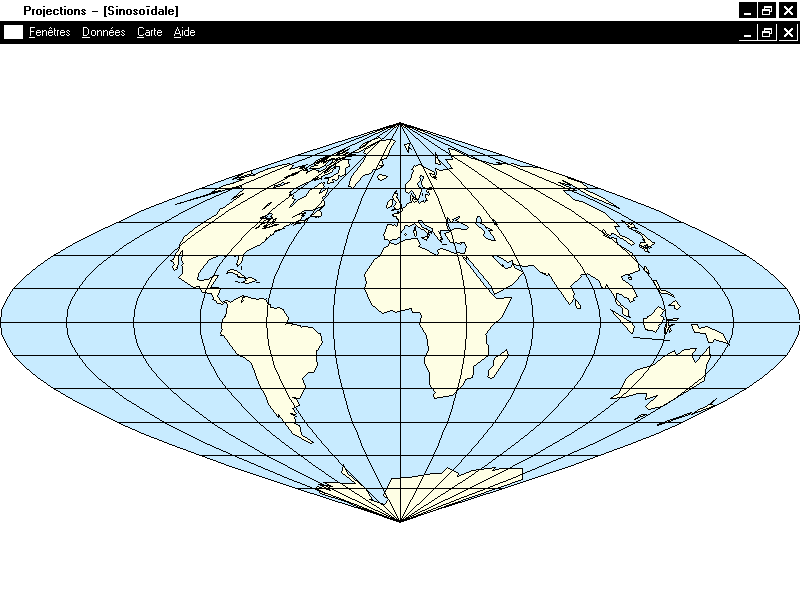
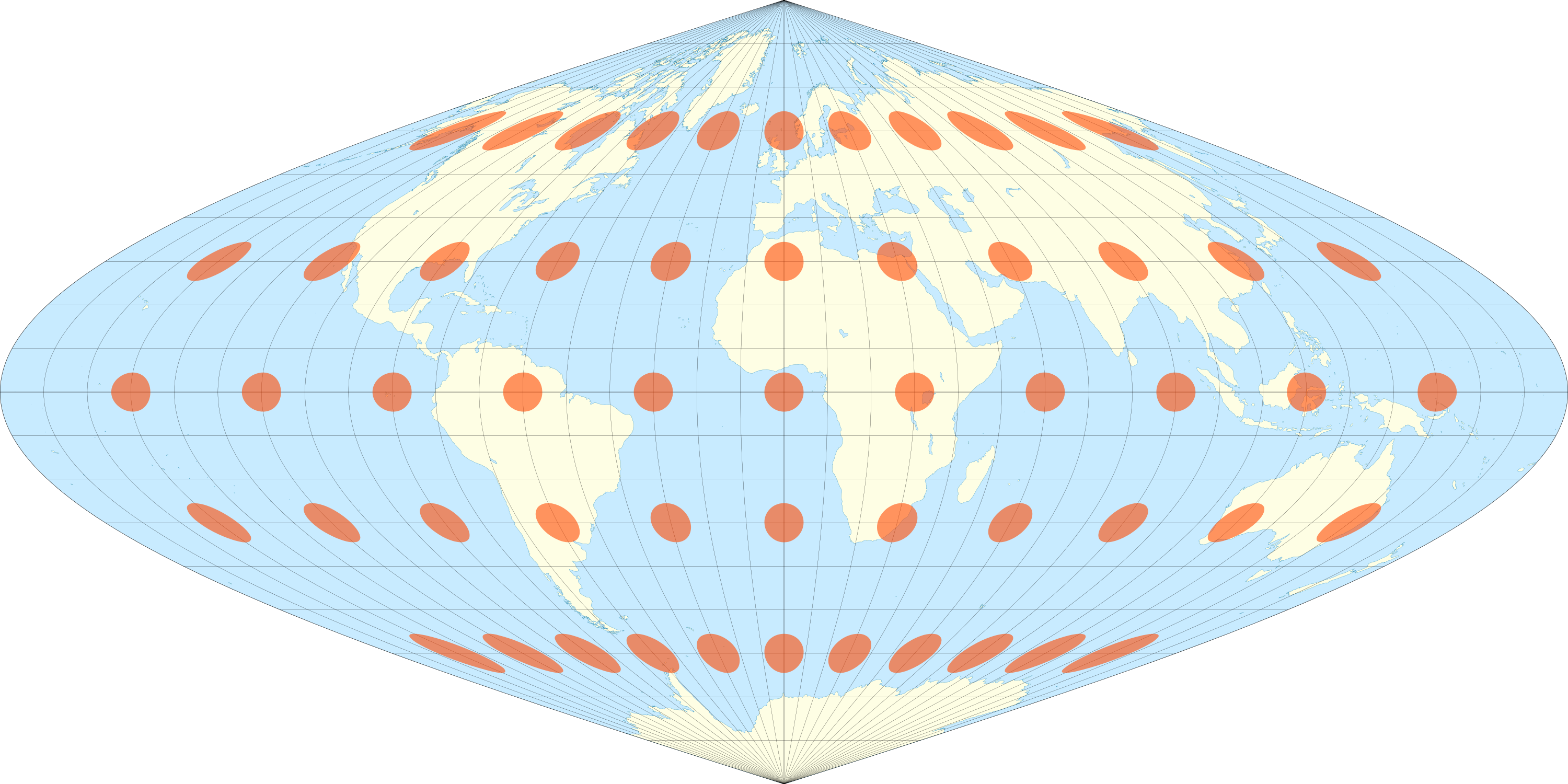
projection qui sera conforme sur l'équateur, qui représentera tous les parallèles par leur véritable
longueur et qui sera équidistante sur le méridien central. Cette projection est appelée
sinusoïdale, ou de Sanson, ou de Flamsteed
(ou encore sinusoïdale de Sanson-Flamsteed).
,
projection qui sera conforme sur l'équateur, qui représentera tous les parallèles par leur véritable
longueur et qui sera équidistante sur le méridien central. Cette projection est appelée
sinusoïdale, ou de Sanson, ou de Flamsteed
(ou encore sinusoïdale de Sanson-Flamsteed).
| Les projections azimutales |