\(\color{blue}\vphantom{\dfrac{1^a}{x_a}}f(x)\!=\!\sin\!\Big(\dfrac{1}{x}\Big)\)

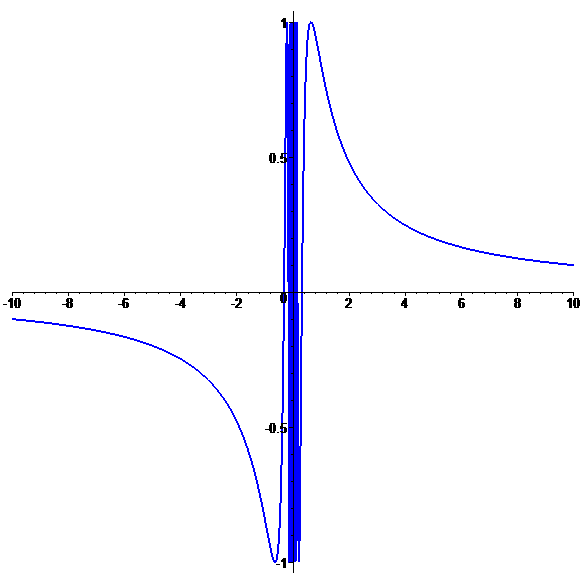
Graphe de \(\color{blue}f\)

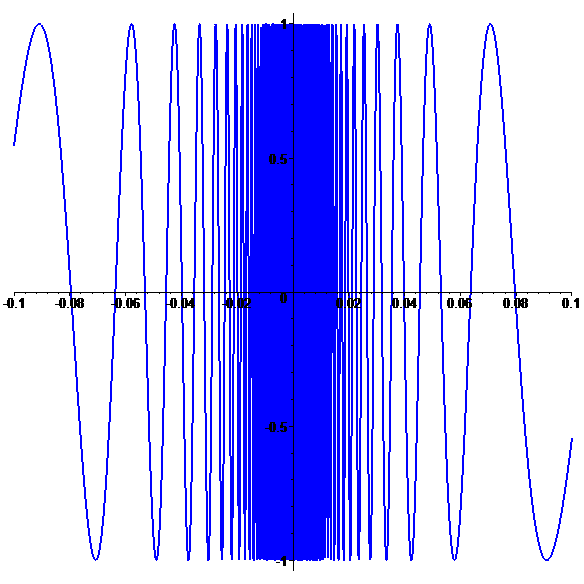
Graphe de \(\color{blue}f\) (zoom)

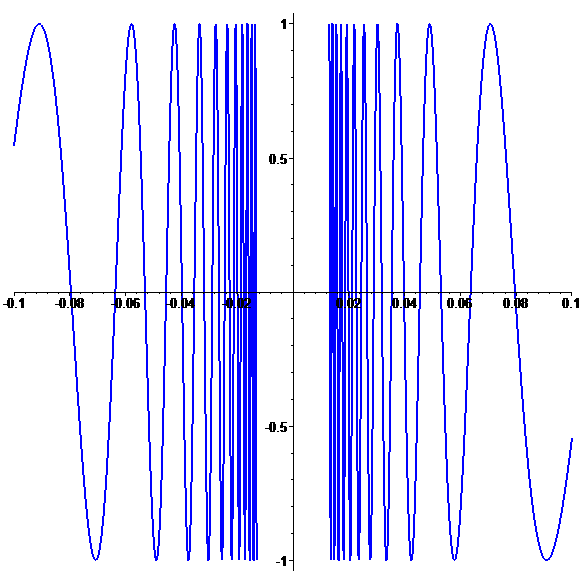
Graphe de \(\color{blue}f\) (méga-zoom)

\(\color{blue}f\) n'est pas prolongeable par continuité en 0

\(\color{red}\vphantom{\dfrac{1^a}{x_a}}g(x)\!=\!x \sin\!\Big(\dfrac{1}{x}\Big)\)

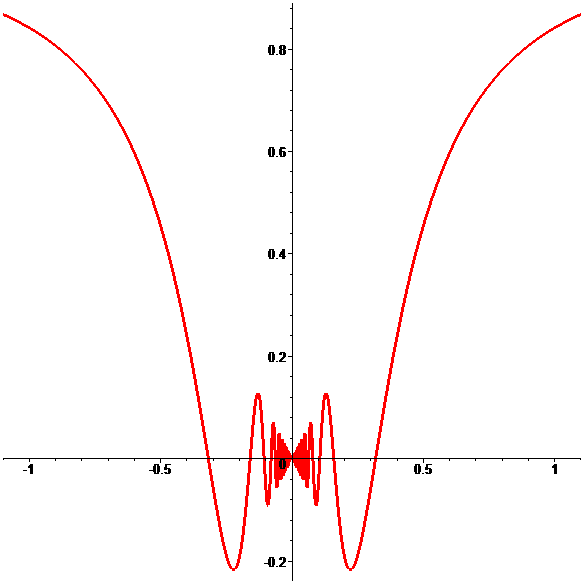
Graphe de \(\color{red}g\)

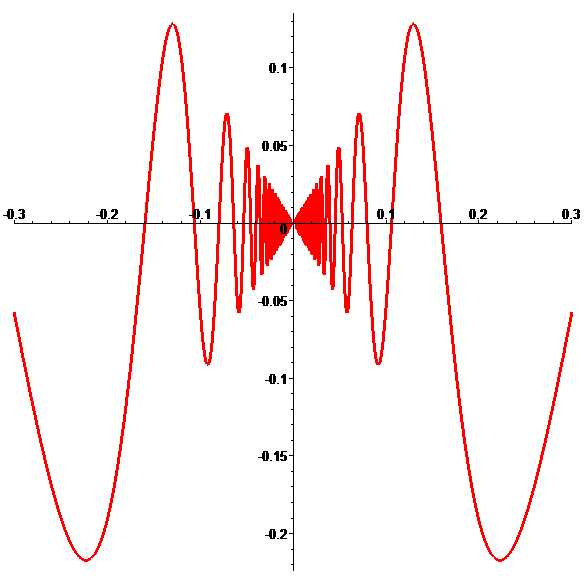
Graphe de \(\color{red}g\) (zoom)

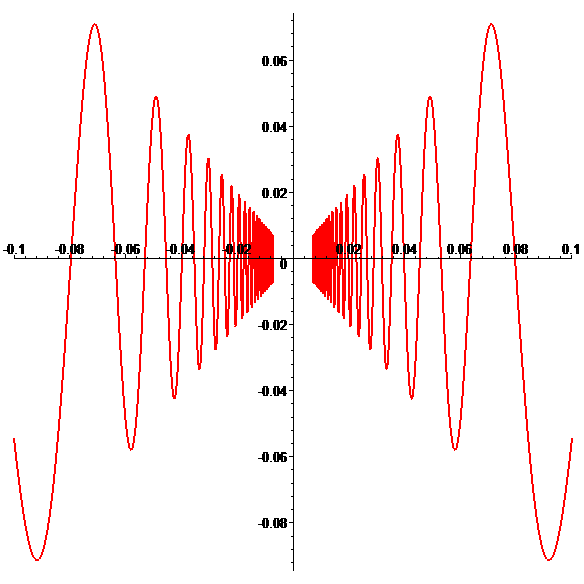
Graphe de \(\color{red}g\) (méga-zoom)

\(\color{red}|g(x)|\leqslant|x|\)
donc \(\color{red}g\) est prolongeable par continuité en 0
en posant \(\color{red}g(0)=0\)