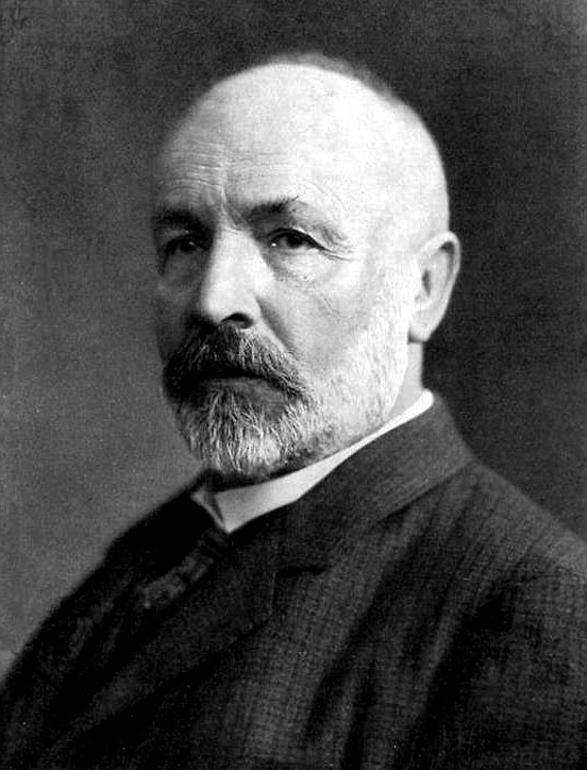| V. Les premiers monstres de l'analyse… |
L'escalier du diable (Cantor, 1885)
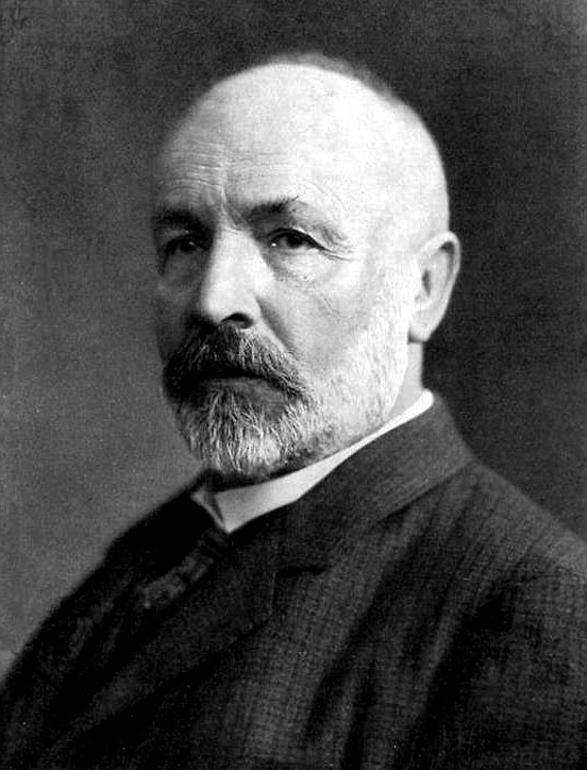 |
| Georg Ferdinand Ludwig Philipp Cantor |
| (1845–1918) |
| Mathématicien allemand |
|
\(f_0(x)\!=\!\frac12\text{ si }x\in[0,1]\)
|
| \(f_{n+1}(x)\!=\!\begin{cases}\vphantom{\dfrac{b}{a}}
\frac12 f_n(3x) & \!\!\scriptstyle\text{si }x\in[0,\frac13]\\
\frac12 & \!\!\scriptstyle\text{si } x\in[\frac13,\frac23]\\
\frac12 f_n(3x\!-\!2)\!+\!\frac12 & \!\!\scriptstyle\text{si } x\in[\frac23,1]
\end{cases}\)
|
|
| \(\displaystyle f\!=\!\lim_{n\to \infty}f_n\) |
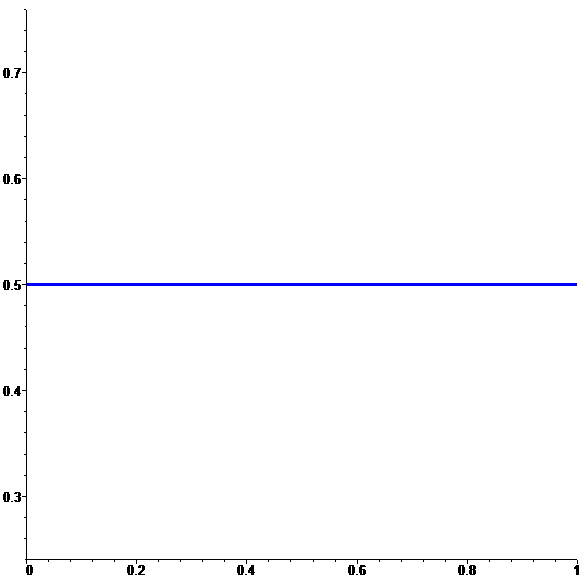
animation 
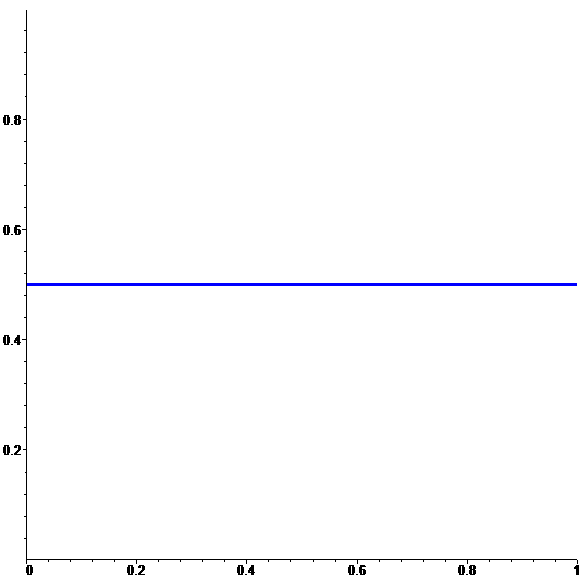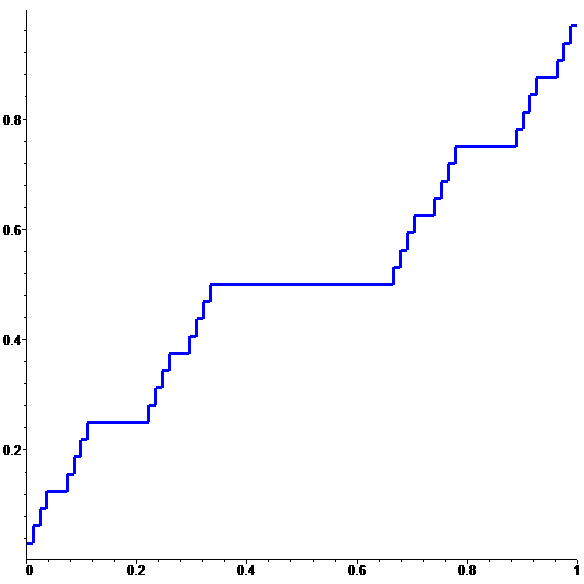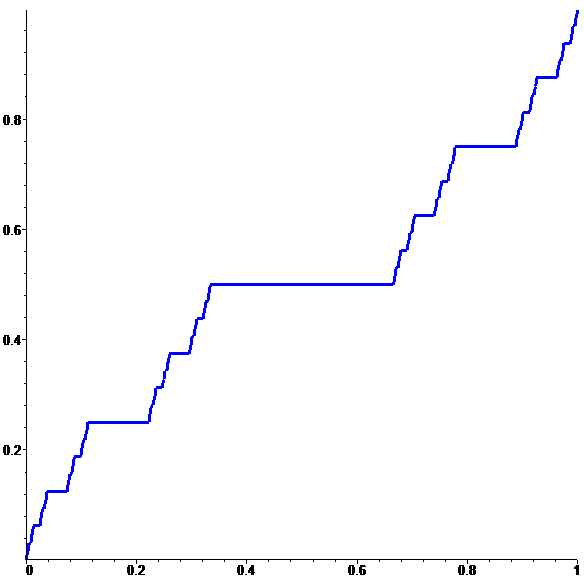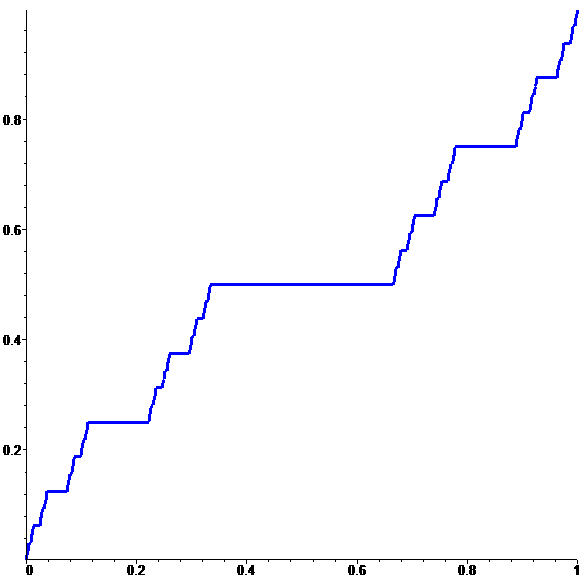
stop 
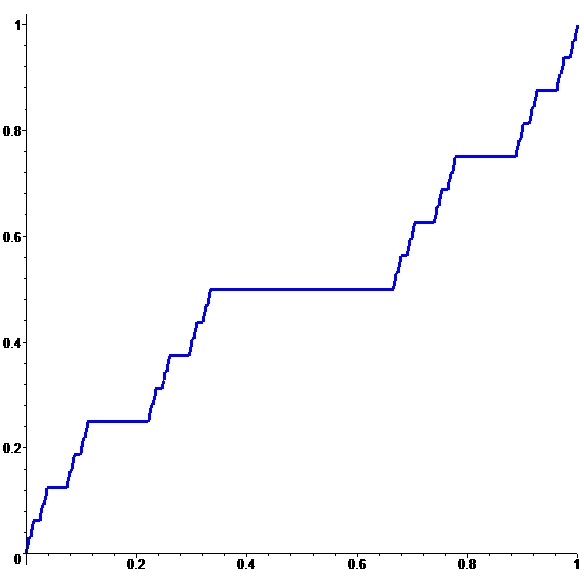
Une fonction continue sur [0,1]
limite de fonctions discontinues…
La courbe de Lebesgue (1904)
 |
| Henri-Léon Lebesgue |
| (1875 – 1941) |
| Mathématicien français |
|
Pour \(t=0,a_1a_2a_3\dots a_{2n}\)
|
|
développement dyadique (en base 2) : \(a_1,a_2,a_3,\ldots\in\{0,1\}\)
|
|
| \(g_n(t)=\begin{cases}\vphantom{\dfrac{a}{a}}
x_n(t)=0,a_1a_3a_5\dots a_{2n-1}\\
y_n(t)=0,a_2a_4a_6\dots a_{2n}
\end{cases}\)
|
|
|
\(\displaystyle g=\lim_{n\to\infty}g_n\)
|
Pour \(n=8 :\)
animation 
Pour \(n\!\in\!\{10,11,12,13,14\}:\)
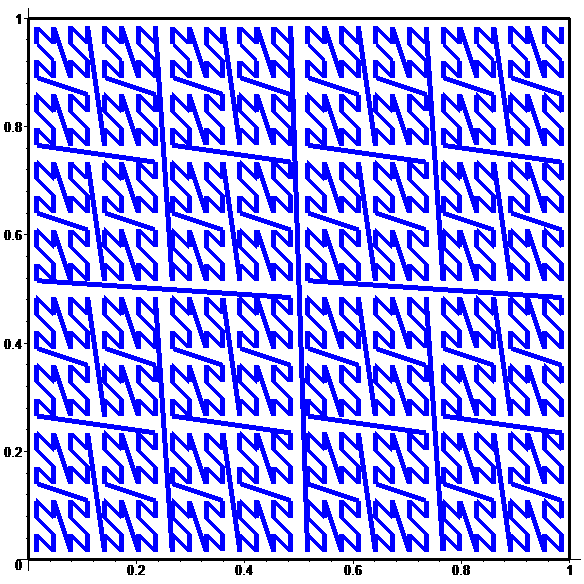
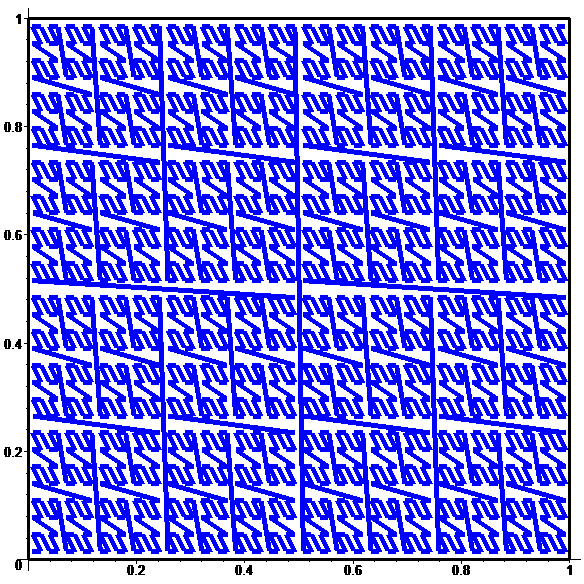
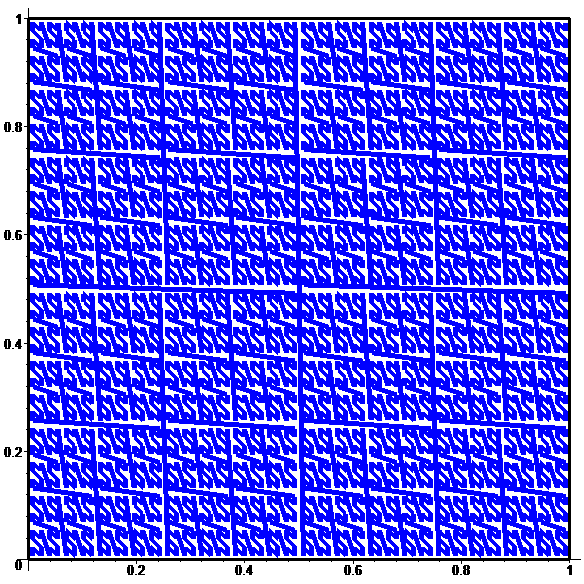
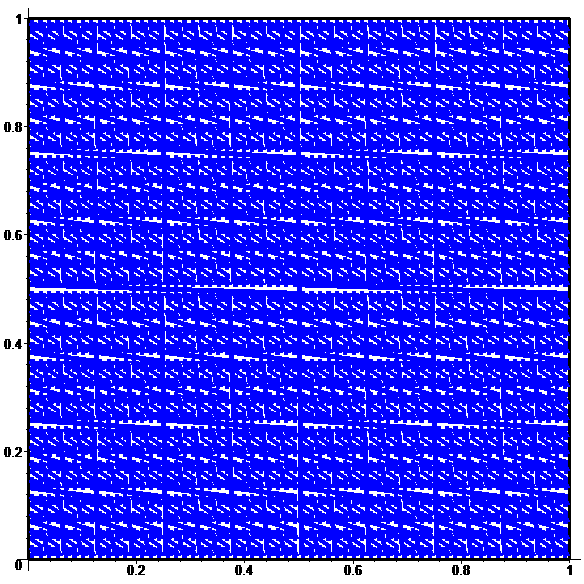
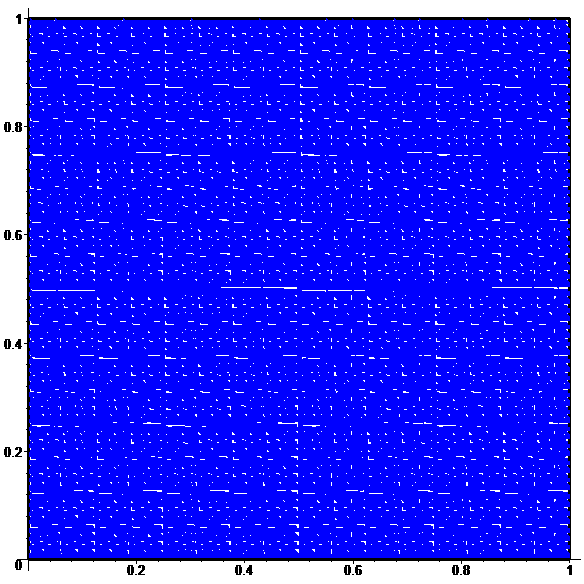
À la limite :
une bijection discontinue
de [0,1] sur [0,1]x[0,1]…
Une courbe remplissant le carré…
La courbe de Peano (1890)
 |
| Giuseppe Peano |
| (1858 – 1932) |
| Mathématicien italien |
|
Pour \(t=0,a_1a_2a_3\dots a_{2n}\)
|
|
développement triadique (en base 3) : \(a_1,a_2,a_3,\ldots\in\{0,1,2\}\)
|
|
|
\(h_n(t)=\begin{cases}\vphantom{\dfrac{a}{a}}
x_n(t)=0,b_1b_3b_5\dots b_{2n-1}\\
y_n(t)=0,c_2c_4c_6\dots c_{2n}
\end{cases}\)
|
|
avec
|
|
\(b_i\!=\!\begin{cases}\vphantom{\dfrac{a}{a}}
a_{2i-1} & \!\!\text{si } a_2\!+\!a_4\!+\!\cdots\!+\!a_{2i-2} \text{ est pair}\\
2-a_{2i} & \!\!\text{si } a_2\!+\!a_4\!+\!\cdots\!+\!a_{2i-2} \text{ est impair}
\end{cases}\)
|
|
et
|
|
\(c_i\!=\!\begin{cases}\vphantom{\dfrac{a}{a}}
a_{2i} & \!\!\text{si } a_1\!+\!a_3\!+\!\cdots\!+\!a_{2i-1} \text{ est pair}\\
2-a_{2i-1} & \!\!\text{si } a_1\!+\!a_3\!+\!\cdots\!+\!a_{2i-1} \text{ est impair}
\end{cases}\)
|
| \(\displaystyle h =\lim_{n\to\infty}h_n\)
|
|
|
Pour \(n=5 :\)
animation 
Pour \(n\!\in\!\{6,7,8,9\} :\)

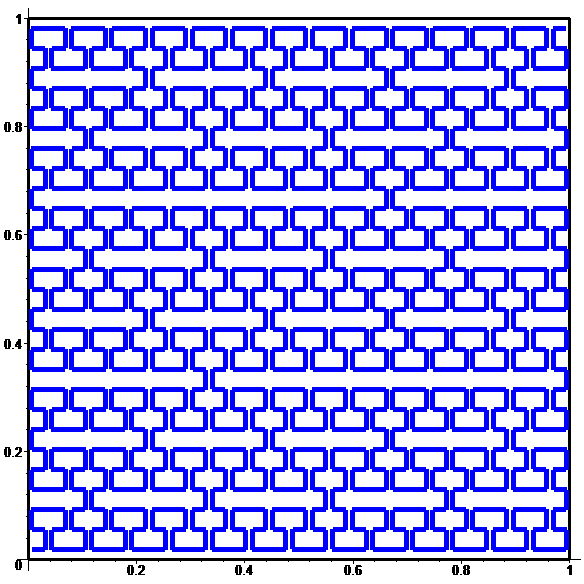

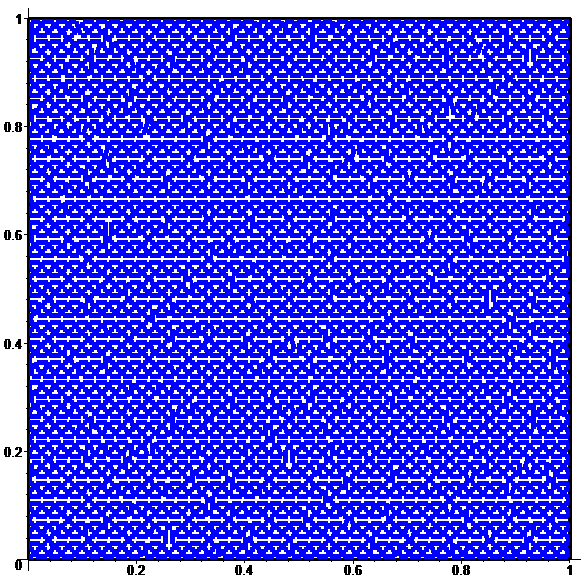
À la limite :
une surjection continue
de [0,1] sur [0,1]x[0,1] (non injective)…
Une autre courbe remplissant le carré…
La courbe de Hilbert (1891)
 |
| David Hilbert |
| (1862 – 1943) |
| Mathématicien allemand |
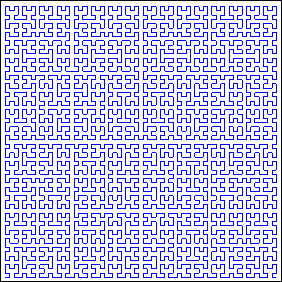

Encore une courbe remplissant le carré !
Théorèmes
[0,1] et [0,1]x[0,1] sont équipotents
(i.e. en bijection)…
|
[0,1] et [0,1]x[0,1]
ne sont pas homéomorphes
(i.e. il n'existe pas de bijection continue entre eux)…
|