IV. Du côté des sin(nx )…



Ondes sinusoïdales de fréquences proportionnelles

À partir d'ondes sinusoïdales
de fréquences multiples d'une même fréquence





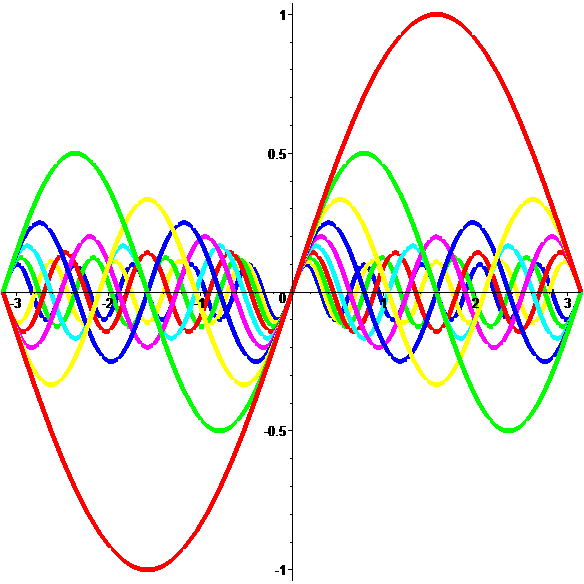
Séries de Fourier


Jean Baptiste Joseph Fourier
(1768–1830)
Mathématicien et physicien français



Série harmonique sinusoïdale

\(\color{blue}\displaystyle\varphi(t)=\sum_{n=1}^{\infty}\frac{\raise -1ex 1}{\raise 0.5ex n} \sin(2\pi \mathbf{f}nt)\)

Signal sonore de fréquence fondamentale \(\mathbf{f}\)



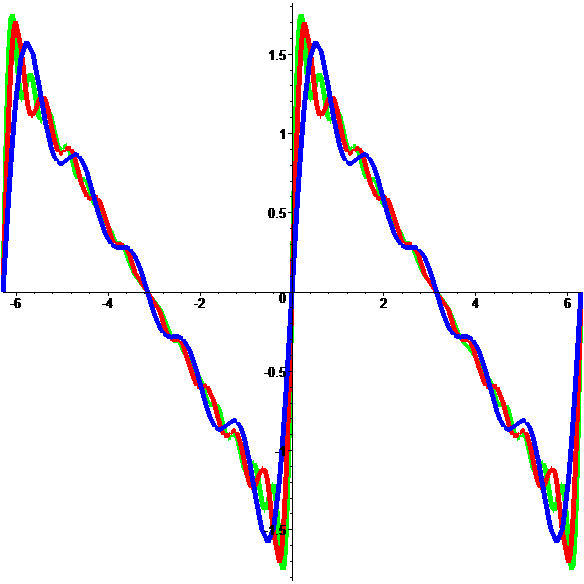
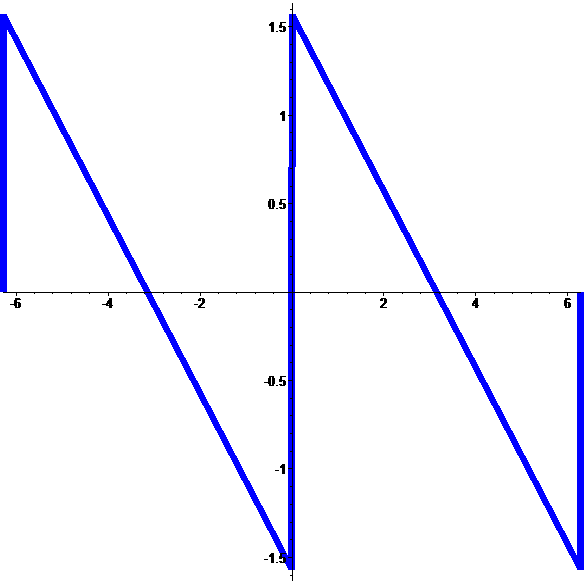
Limite discontinue
d'une suite de fontions continues…









Série harmonique sinusoïdale partielle

\(\color{red}\displaystyle\psi(t) = \sum_{n=1}^{\infty}\frac{\raise -1ex 1}{\raise 0.5ex {2n\!+\!1}} \sin(2\pi\mathbf{f}(2n\!+\!1)t)\)

Signal sonore de fréquence fondamentale \(\mathbf{f}\)



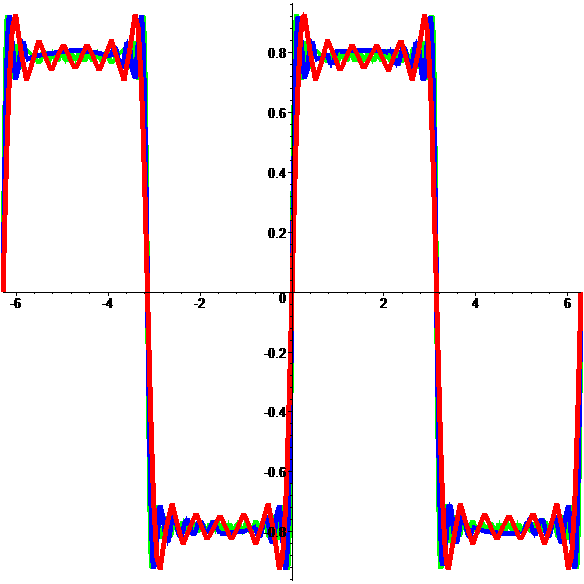
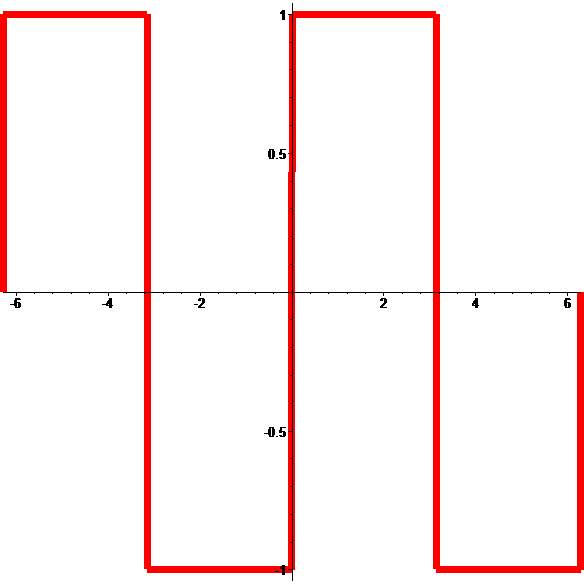
Limite discontinue
d'une suite de fontions continues…




   
◄ Sommaire ►