Exemples

Aimé Lachal Équations différentielles linéaires 1^er ordre (coefficients constants)

I. Équations différentielles
linéaires du 1^er ordre
à coefficients constants

Résolution de \(\dot{u}(t)+au(t)=\varphi(t)\)
et tracé des courbes intégrales

Solution générale

Hypothèse : \(a\!\in\!\mathbb{R}\) et \(\varphi\) est une fonction continue sur l'intervalle \(I\) à valeurs réelles ou complexes. On fixe un \(t_0\!\in\! I\).

\(u(t)\!=\!\lambda\, e^{-at}\!+\!\int_{t_0}^t\varphi(s) \,\mathrm{e}^{-a(t-s)}\,\mathrm{d}s, \;\lambda\!\in\!\mathbb{R}\)

Interprétation : \(u\!=\!u_{_H}\!+u_{_P}\) où

\(u_{_H}\) est la solution générale de l'équation homogène associée \(\dot{u}(t)+au(t)=0 :\) \(u_{_H}(t)\!=\!\lambda\, e^{-at},\;\lambda\!\in\!\mathbb{R}~;\)

\(u_{_P}\) est une solution particulière de l'équation initiale : \(u_{_P}(t)\!=\!\int_{t_0}^t\varphi(s) \,\mathrm{e}^{-a(t-s)}\,\mathrm{d}s.\)

Cas particulier :

Cas d'un second membre de type « polynôme-exponentiel » : \(\varphi(t)=P(t)\mathrm{e}^{\alpha t}\) où \(P\) est un polynôme de degré \(d\!\in\!\mathbb{N}\) à coefficients réels ou complexes et \(\alpha\!\in\!\mathbb{R}\) ou \(\mathbb{C}.\)
Il existe une solution particulière de la forme

\(u_{_P}(t)=Q(t)\mathrm{e}^{\alpha t}\) si \(\alpha\neq -a,\)

\(u_{_P}(t)=tQ(t)\mathrm{e}^{\alpha t}\) si \(\alpha=-a\) (cas de « résonance »),

où \(Q\) est un polynôme de degré \(d.\)

Sous-cas particuliers :

Cas d'un second membre polynomial de degré \(d\!\in\!\mathbb{N}:\)
il existe une solution particulière polynomiale

de degré \(d\) si \(a\neq 0~;\)

de degré \(d+1\) si \(a=0.\)

Cas d'un second membre exponentiel : \(\varphi(t)=A\,\mathrm{e}^{\alpha t}\) où \(A\!\in\!\mathbb{R}\) ou \(\mathbb{C}.\)
Une solution particulière est donnée par

\(u_{_P}(t)=\frac{A}{a+\alpha}\,\mathrm{e}^{\alpha t}\) si \(\alpha\neq -a~;\)

\(u_{_P}(t)=At\,\mathrm{e}^{-at}\) si \(\alpha=-a\) (cas de « résonance »).

Cas d'un second membre trigonométrique : \(\varphi(t)=A\,\cos(\omega t)+B\,\sin(\omega t)\) où \(A,B\!\in\!\mathbb{R}\) et \(\omega\!\in\!\mathbb{R}^*.\)
Une solution particulière est donnée par

\(u_{_P}(t)=A\,\Re \mathrm{e}\left(\frac{1}{a+\mathrm{i}\omega}\,\mathrm{e}^{\mathrm{i}\omega t}\right) +B\,\Im \mathrm{m}\left(\frac{1}{a+\mathrm{i}\omega}\,\mathrm{e}^{\mathrm{i}\omega t}\right)\)
\(\phantom{u_{_P}(t)}=\frac{Aa-B\omega}{a^2+\omega^2}\cos(\omega t)+\frac{A\omega+Ba}{a^2+\omega^2}\sin(\omega t).\)

Principe de superposition : si \(u_1\) (resp. \(u_2\)) est solution de \(\dot{u}(t)+au(t)=\varphi_1(t)\) (resp. \(\dot{u}(t)+au(t)=\varphi_2(t)\)), alors \(\alpha_1u_1\!+\!\alpha_2u_2\) est solution de \(\dot{u}(t)+au(t)=\alpha_1\varphi_1(t)\!+\!\alpha_2\varphi_2(t)\).

\(\vphantom{()_p^b}\)   \(a=6\qquad \varphi(t)=3\,\mathrm{e}^{-3t}\hspace{-0.1em}+\hspace{-0.1em}6\)

Solution : \(u(t)\!=\!\lambda\,\mathrm{e}^{-6t}\!+\hspace{-0.1em}\mathrm{e}^{-3t}\hspace{-0.1em}+\hspace{-0.1em}1\)

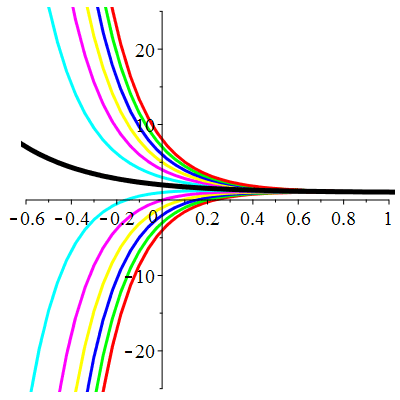
\(\vphantom{()_p^b}\)   \(a=3\qquad \varphi(t)=\hspace{-0.1em}\mathrm{e}^{-3t}\)

Solution : \(u(t)\!=(t+\!\lambda)\mathrm{e}^{-3t}\)

\(\vphantom{()_p^b}\)   \(a=2\qquad \varphi(t)=5\sin(t)\)

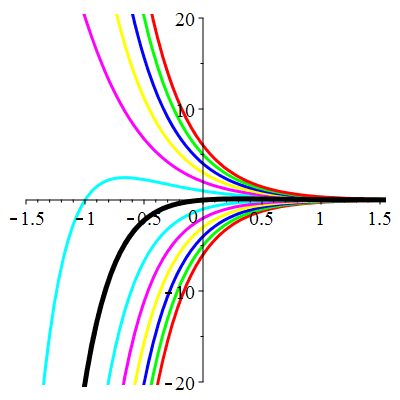
Solution : \(u(t)\!=\!\lambda\,\mathrm{e}^{-2t}\!-\!\cos(t)\!+\!2\sin(t)\)

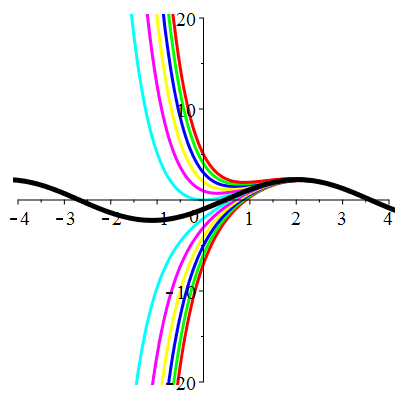
\(\vphantom{()_p^b}\)   \(a=1\qquad \varphi(t)=2\,\mathrm{e}^{-t}\cos(2t)\)

Solution : \(u(t)\!=\!\lambda\,\mathrm{e}^{-t}\!+\hspace{-0.1em}\mathrm{e}^{-t}\sin(2t)\)

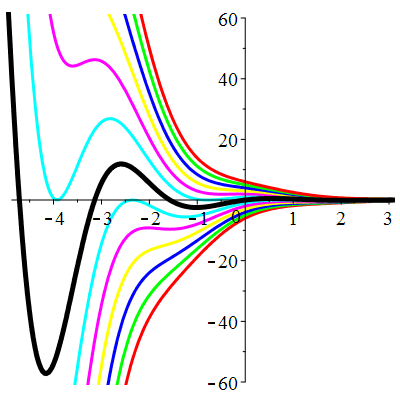
\(\vphantom{()_p^b}\)   \(a=1\qquad \varphi(t)=4\,\mathrm{e}^{t}\cos(2t)\)

Solution : \(u(t)\!=\!\lambda\,\mathrm{e}^{-t}\!+\hspace{-0.1em}\mathrm{e}^t\big[\cos(2t)\!+\!\sin(2t)\big]\)

\(\vphantom{()_p^b}\)   \(a=1\qquad \varphi(t)=2\cos(t)\)

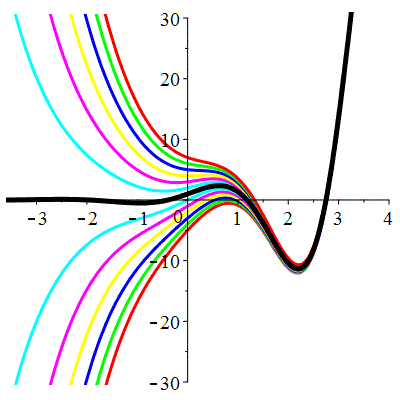
Solution : \(u(t)\!=\!\lambda\,\mathrm{e}^{-t}\!+\!\cos(t)\!+\!\sin(t)\)

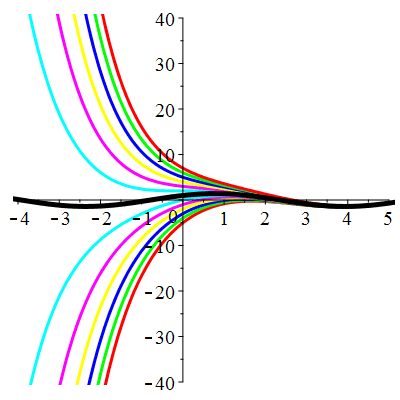
\(\vphantom{()_p^b}\)   \(a=1\qquad \varphi(t)=10\cos(3t)\)

Solution : \(u(t)\!=\!\lambda\,\mathrm{e}^{-t}\!+\!\cos(3t)\!+\!3\sin(3t)\)

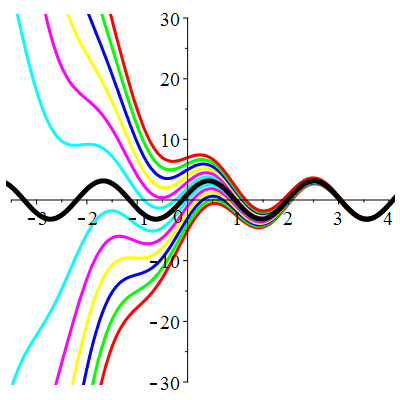
\(\vphantom{()_p^b}\)   \(a=1\qquad \varphi(t)=40\cos^3(t)\)

Solution : \(u(t)\!=\!\lambda\,\mathrm{e}^{-t}\!+\!15\cos(t)\!+\!15\sin(t)\!+\hspace{-0.3em}\cos(3t)\!+\!3\sin(3t)\)

\(\vphantom{()_p^b}\)   \(a=1\qquad \varphi(t)=2t^2-4t+1\)

Solution : \(u(t)\!=\!\lambda\,\mathrm{e}^{-t}\!+\!t^2\!-\!4t\!+1\)

\(\vphantom{()_p^b}\)   \(a=1\qquad \varphi(t)=t\,\mathrm{e}^{-2t}\)

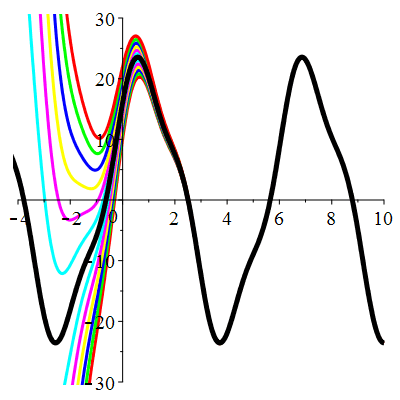
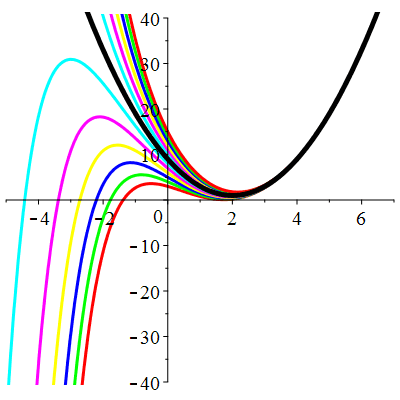
Solution : \(u(t)\!=\!\lambda\,\mathrm{e}^{-t}\!-\!(t+\!1)\mathrm{e}^{-2t}\)

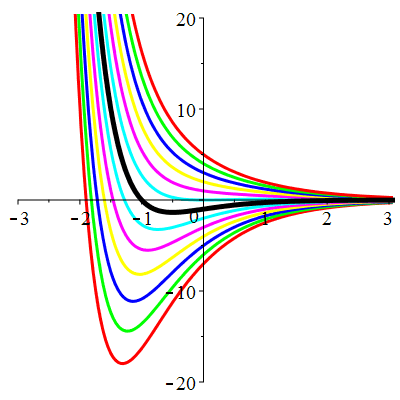
\(\vphantom{()_p^b}\)   \(a=1\qquad \varphi(t)=2t\,\mathrm{e}^{-t}\)

Solution : \(u(t)\!=\!(t^2\!+\!\lambda)\mathrm{e}^{-t}\)

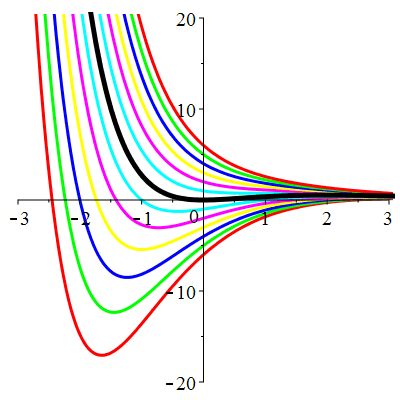
\(\vphantom{()_p^b}\)   \(a=1\qquad \varphi(t)=8t\,\mathrm{e}^{-3t}\cos(2t)\)

Solution : \(u(t)\!=\!\lambda\,\mathrm{e}^{-t}\!+\!\mathrm{e}^{-3t}\big((2t\!+\!1)\sin(2t)\!-\!2t\cos(2t)\big)\)

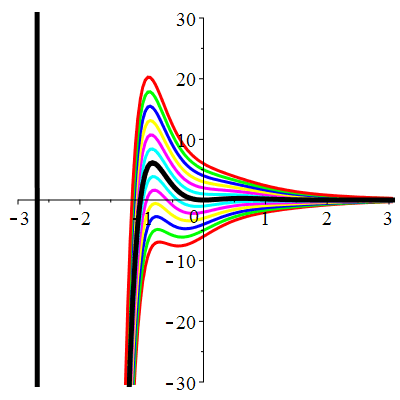
\(\vphantom{()_p^b}\)   \(a=1\qquad \varphi(t)=t\,\mathrm{e}^{-t}\cos(t)\)

Solution : \(u(t)\!=\!\mathrm{e}^{-t}(\cos(t)\!+\!t\sin(t)\!+\!\lambda)\)

◄ Sommaire ►