-

Aimé Lachal Équations différentielles linéaires 1er ordre (coefficients variables)
Résolution de \(\dot{u}(t)+a(t)u(t)=\varphi(t)\)
et tracé des courbes intégrales
| \(u(t)\!=\!\lambda\, e^{-A(t)}\!+\!\int_{t_0}^t\varphi(s) \,\mathrm{e}^{-\big(A(t)-A(s)\big)}\,\mathrm{d}s,\;\lambda\!\in\!\mathbb{R}\) |
| \(u(t)\!=\!u_0\, e^{-\big(A(t)-A(t_0)\big)}\!+\!\int_{t_0}^t\varphi(s) \,\mathrm{e}^{-\big(A(t)-A(s)\big)}\,\mathrm{d}s\) |
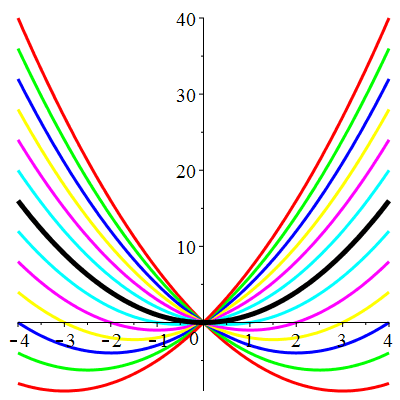
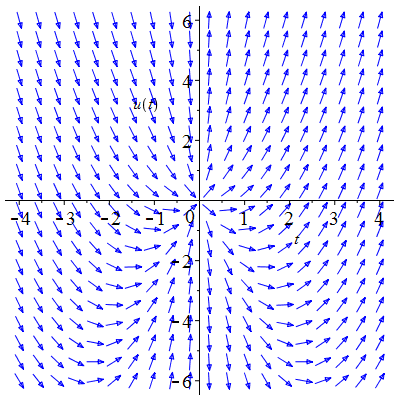
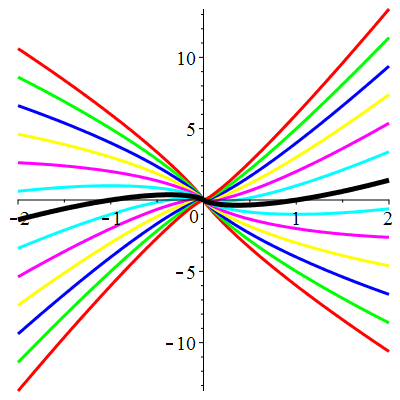
| Solution : | \(u(t)\!=\!1\!+\!\lambda\,\mathrm{e}^{-\frac12t^2}\) |
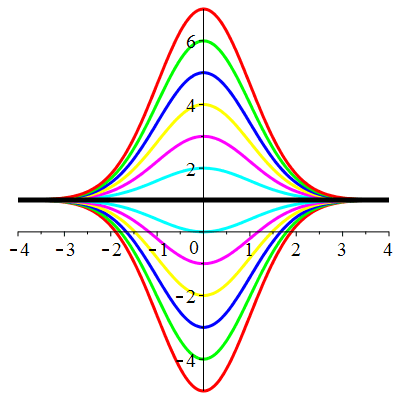
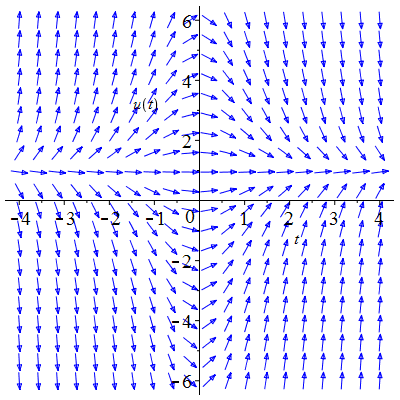
| Solution : | \(u(t)\!=\!-1\!+\!\lambda\,\mathrm{e}^{\frac12t^2}\) |
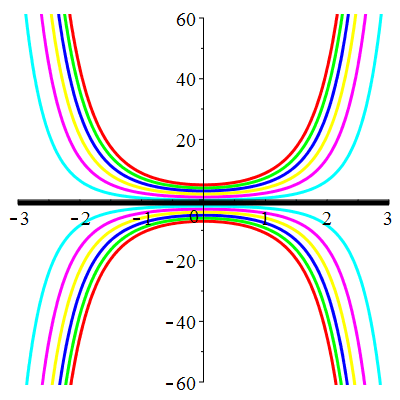
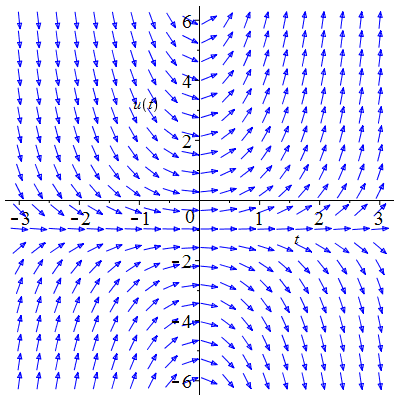
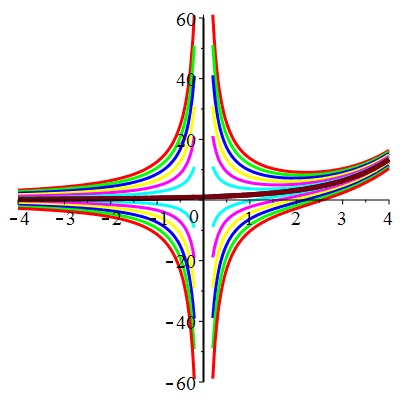
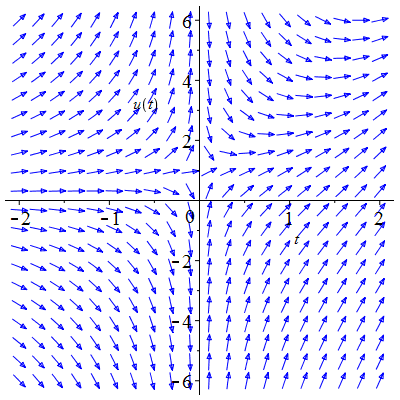
| Solution : | \(u(t)\!=\!1\!+\!\lambda\,\mathrm{e}^{-\frac13t^3}\) |
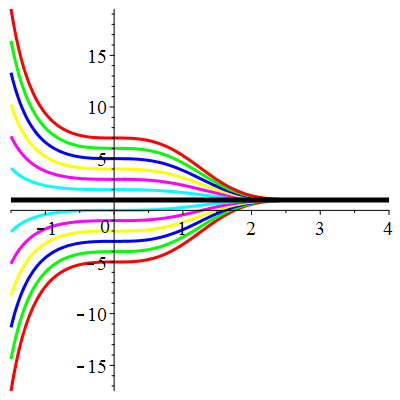
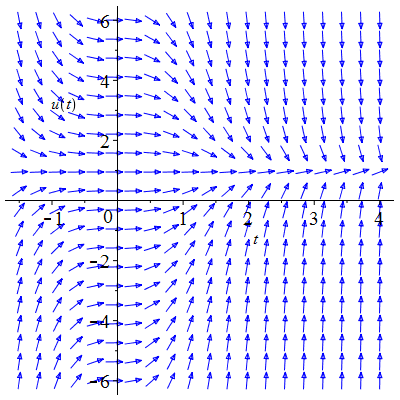
| Solution : |
| ||
|
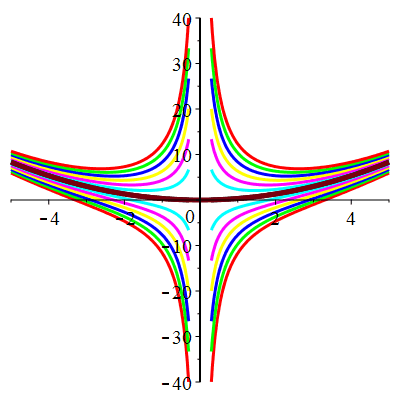
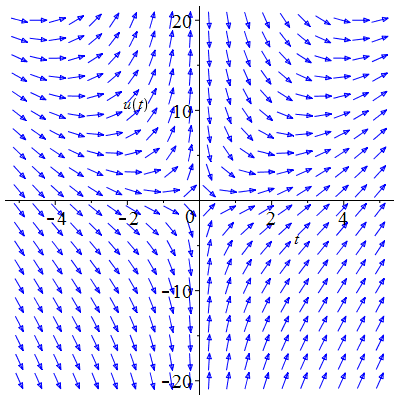
| Solution : |
| ||
|
| Solution : |
| ||
|
| Solution : |
| ||
|
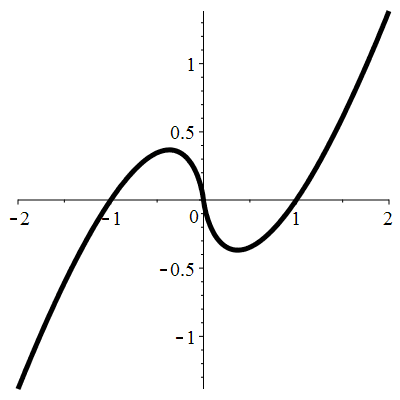
| Solution : |
| ||||||
|
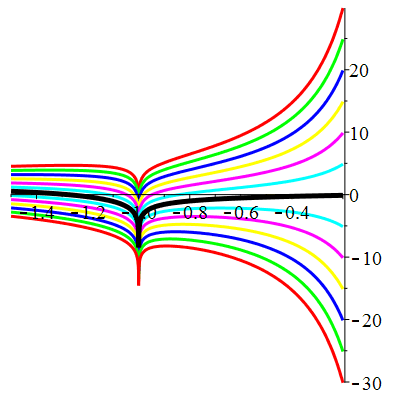
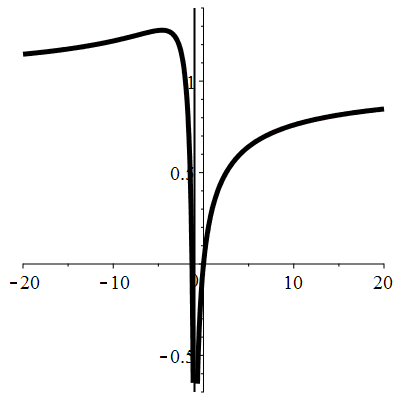
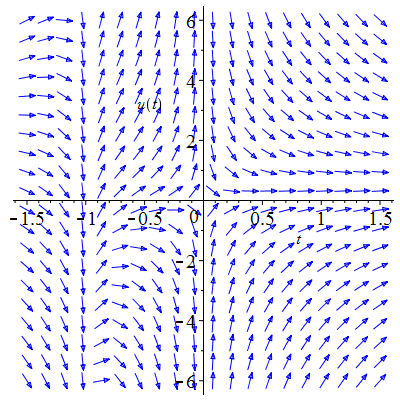
| Solution : |
| ||||||
|
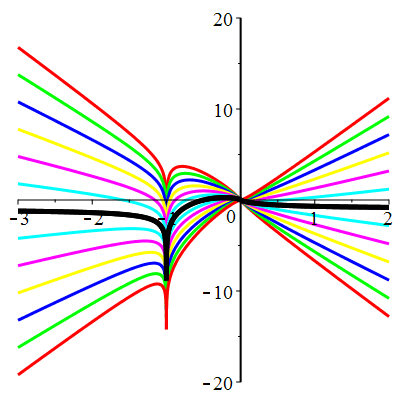
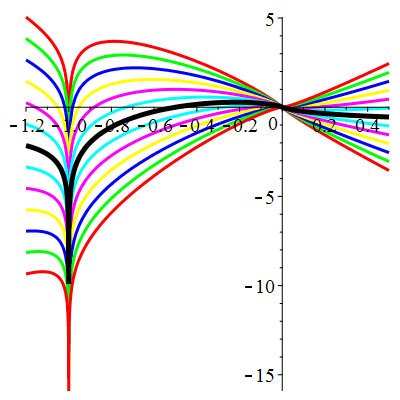
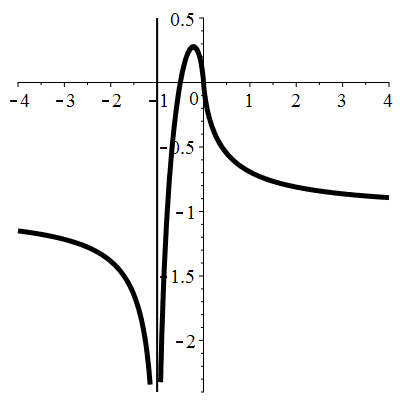
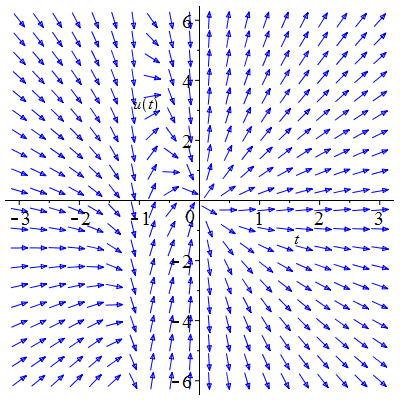
| Solution : |
| |||||
|
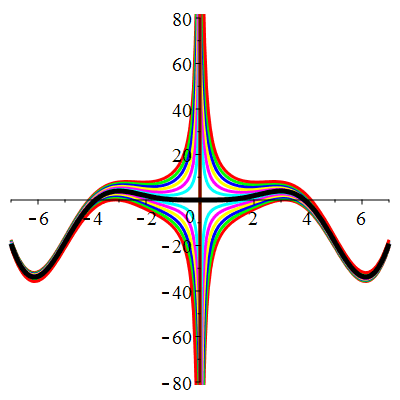
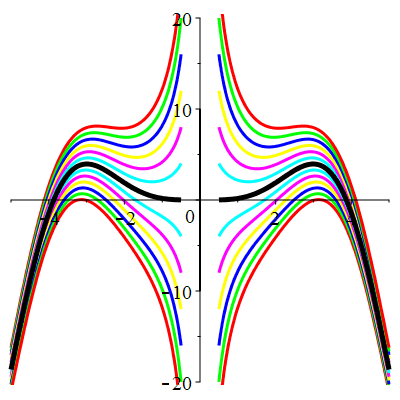
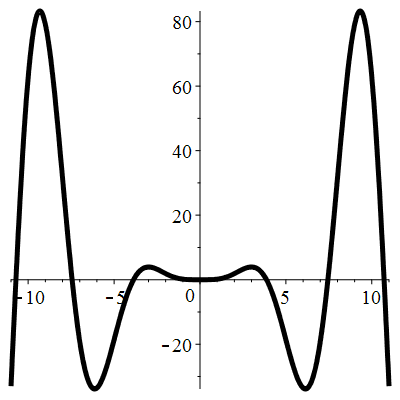
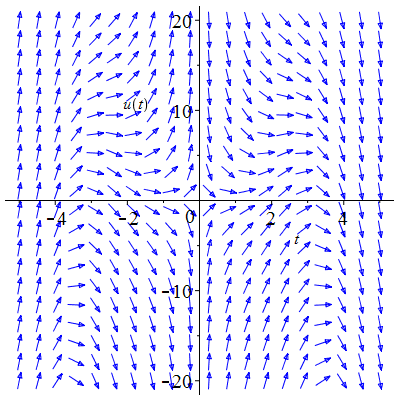
| Solution : |
| |||
|
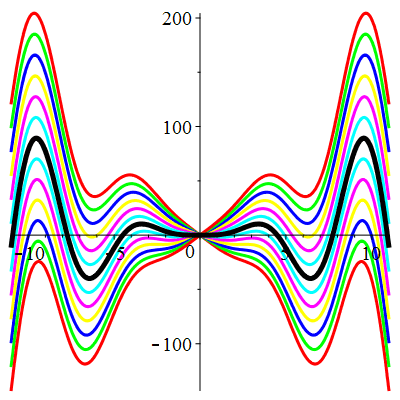
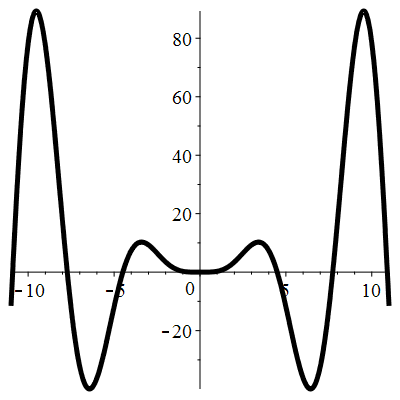
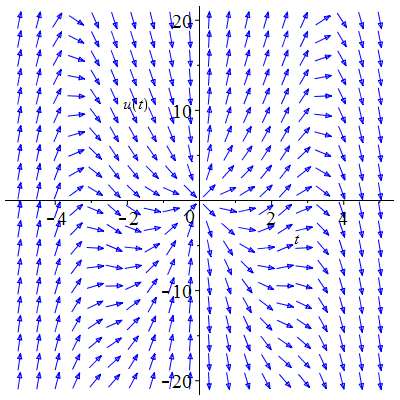
| Solution : |
|
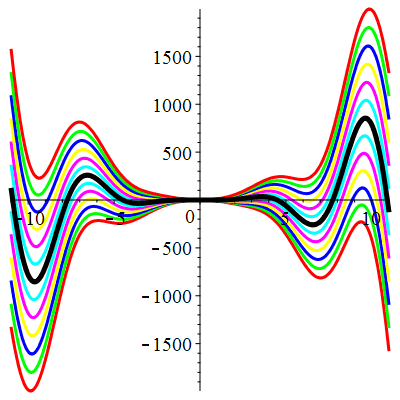
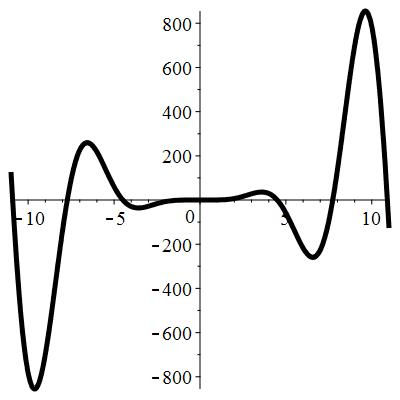
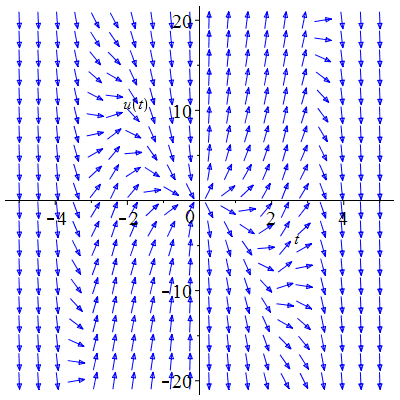
| Solution : |
| |||
|
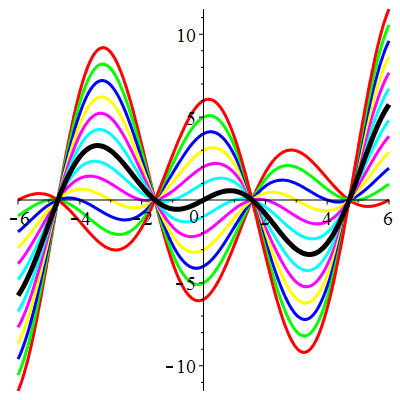
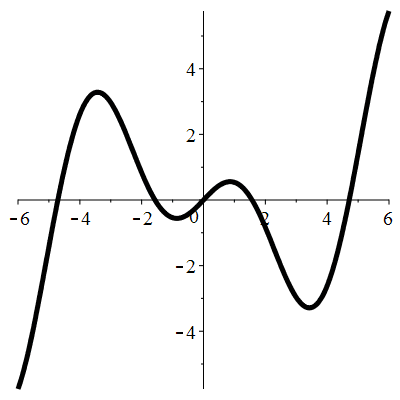
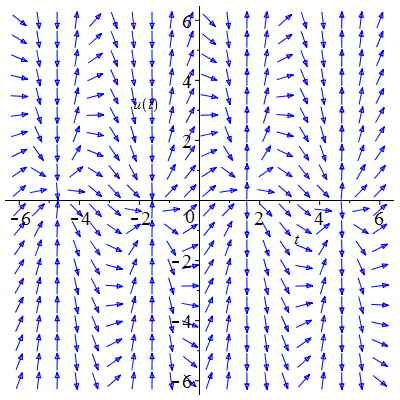
| Solution : |
| |||
|
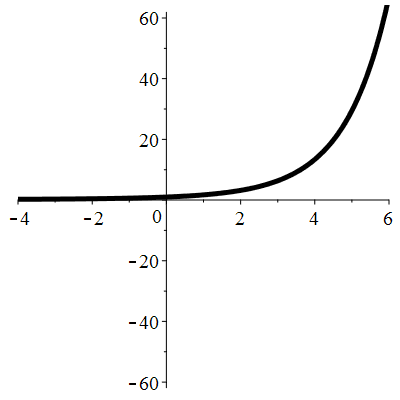
| Solution : |
| |||
|
| ◄ | Sommaire | ► |