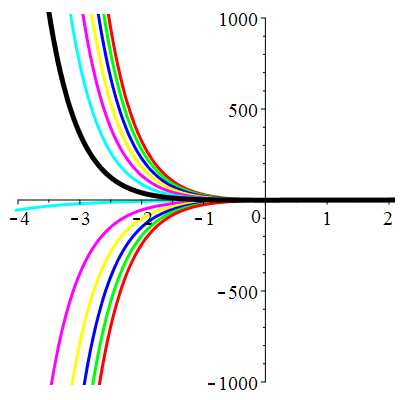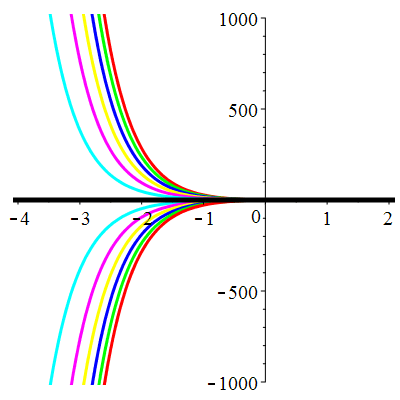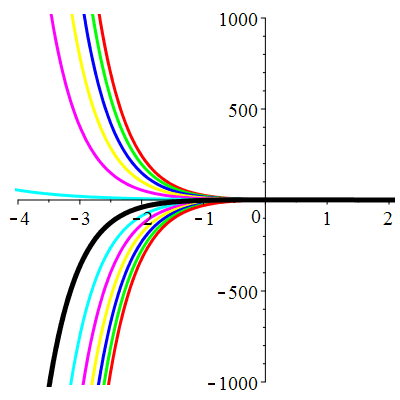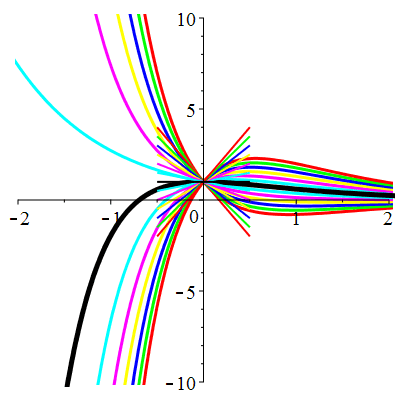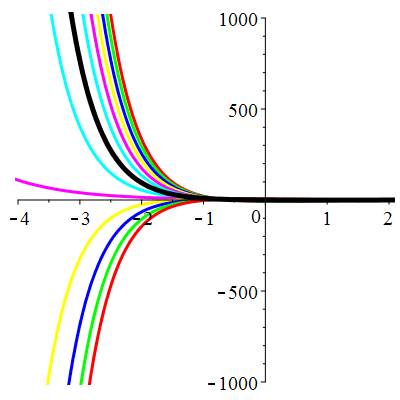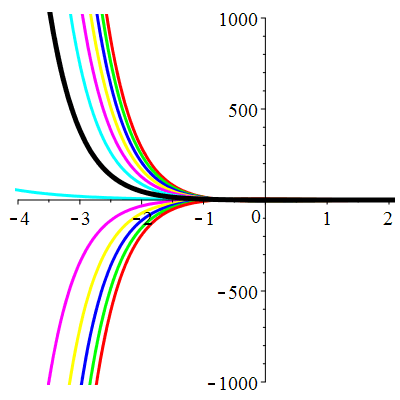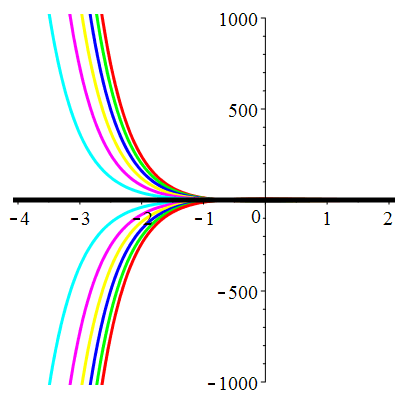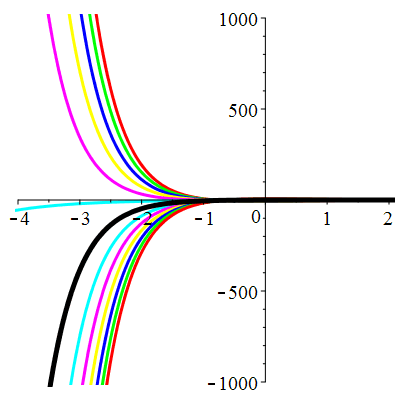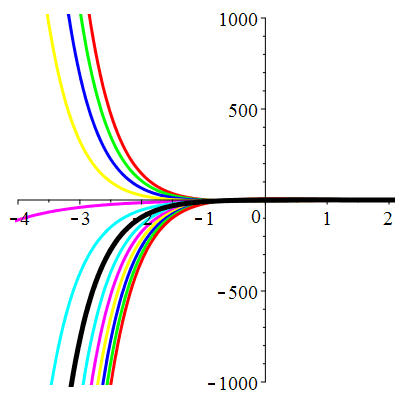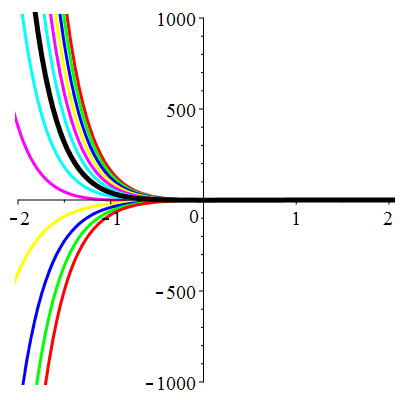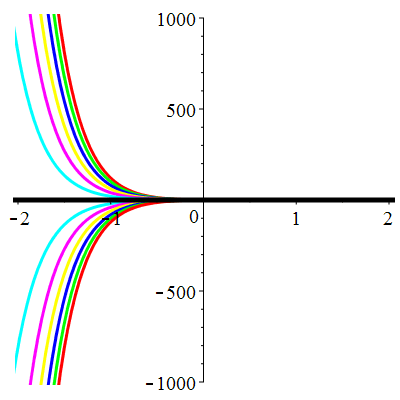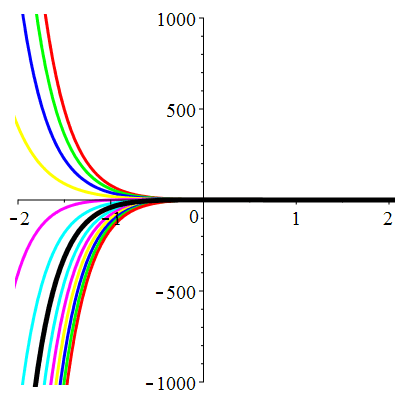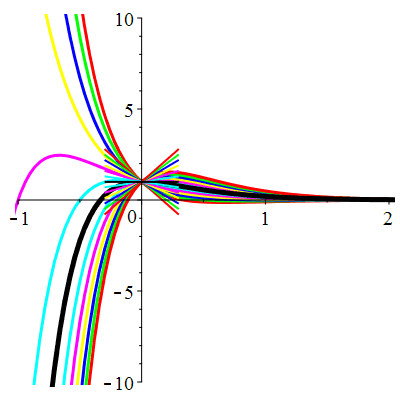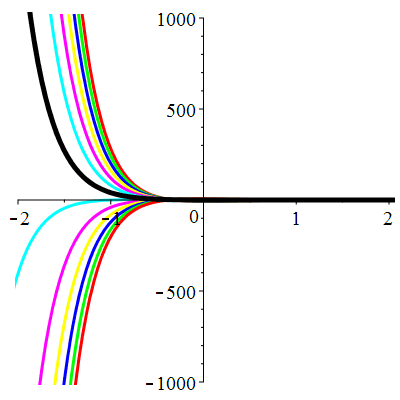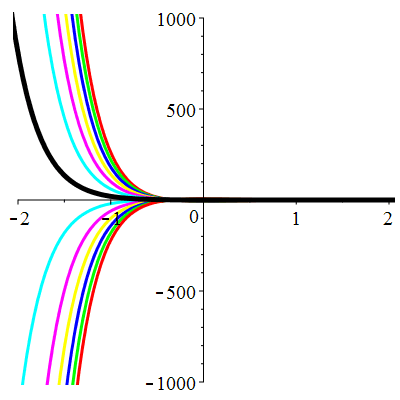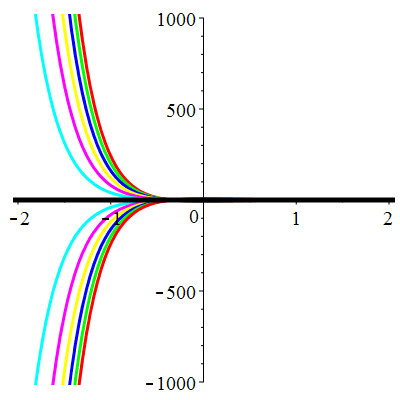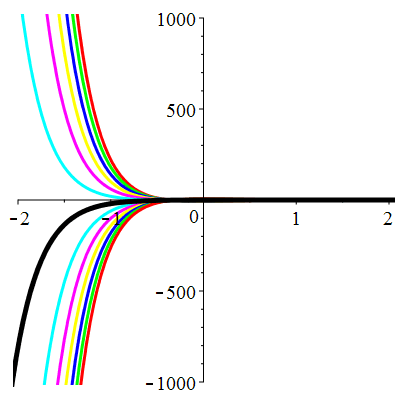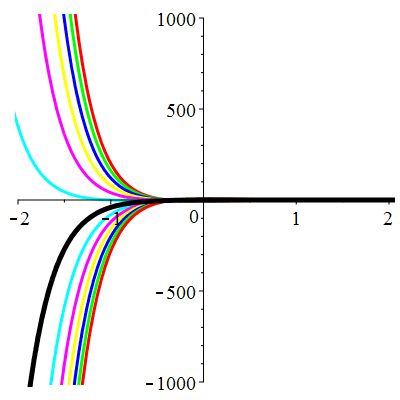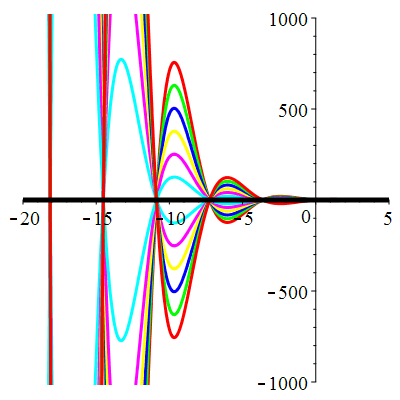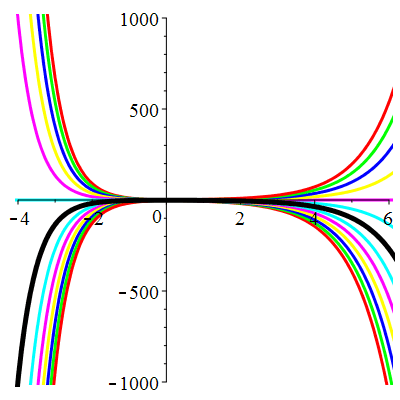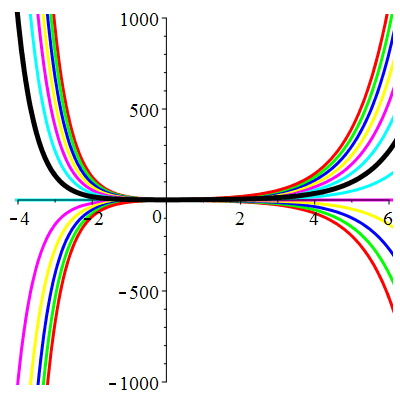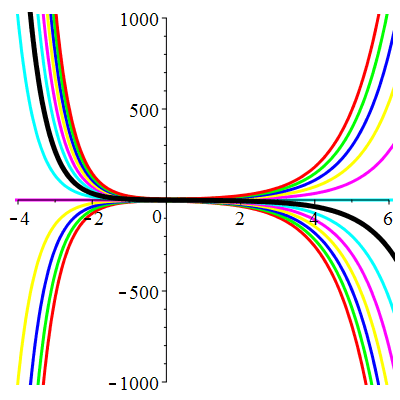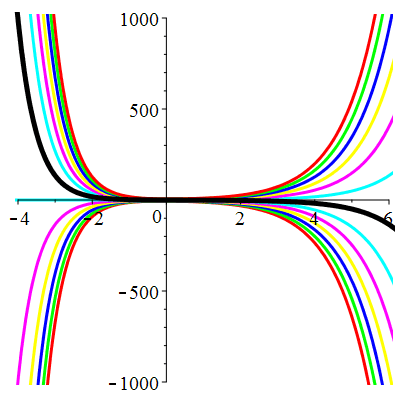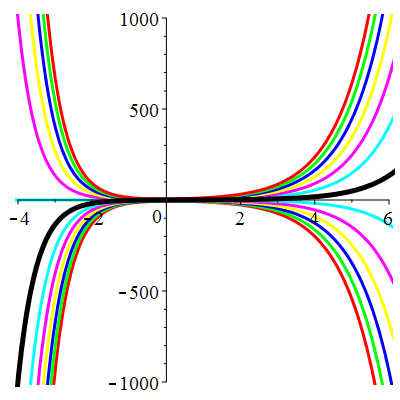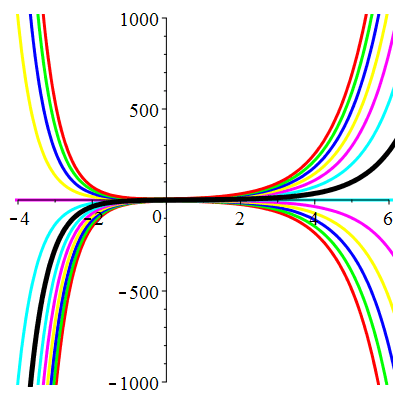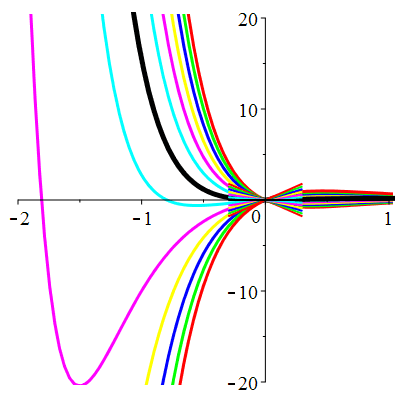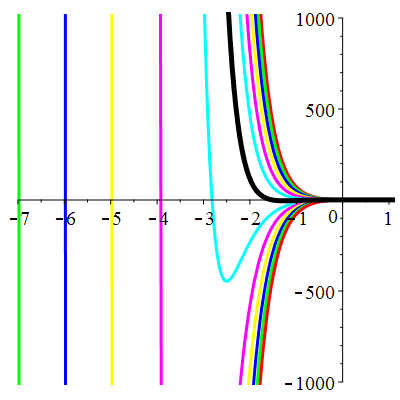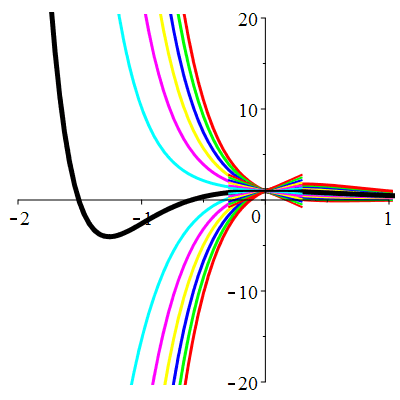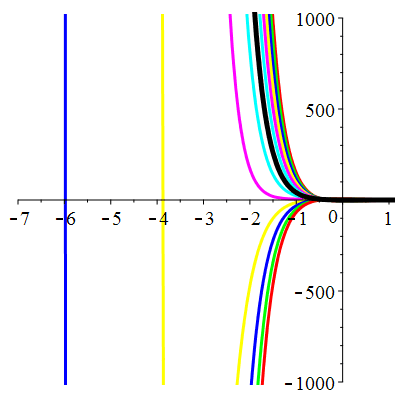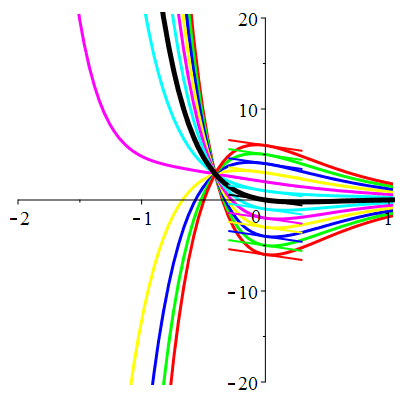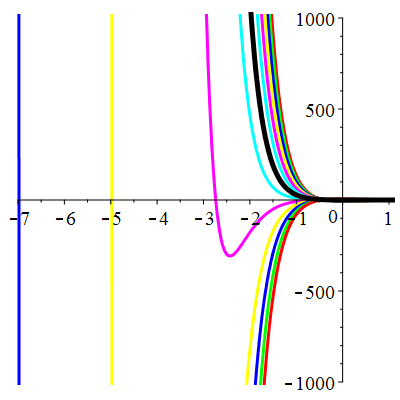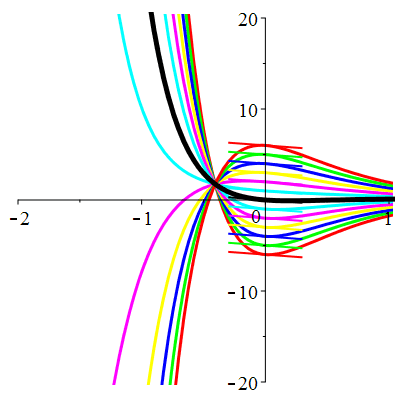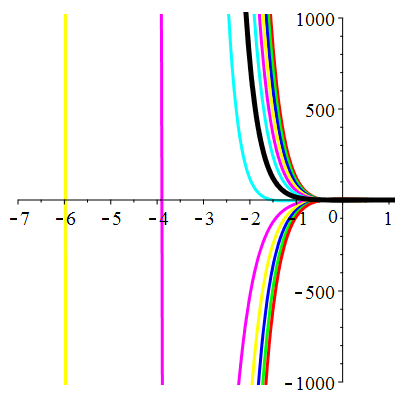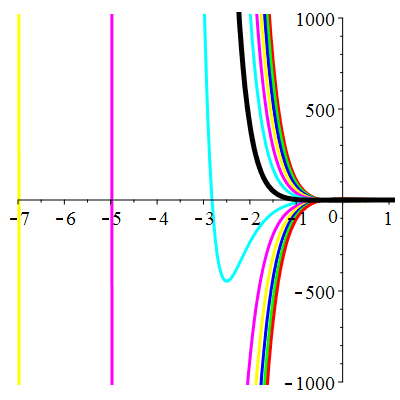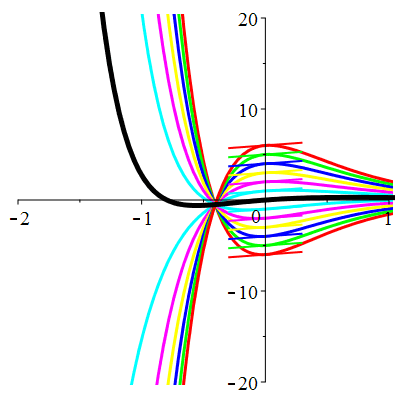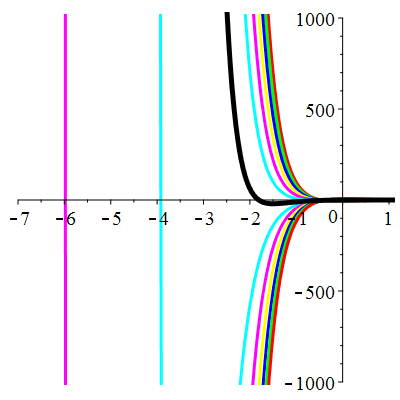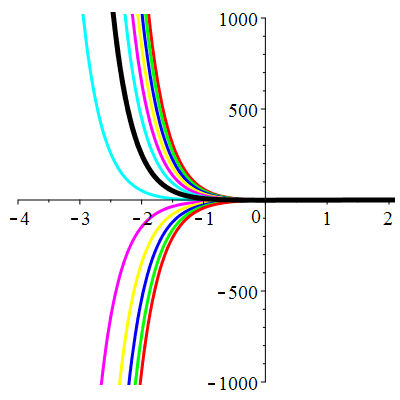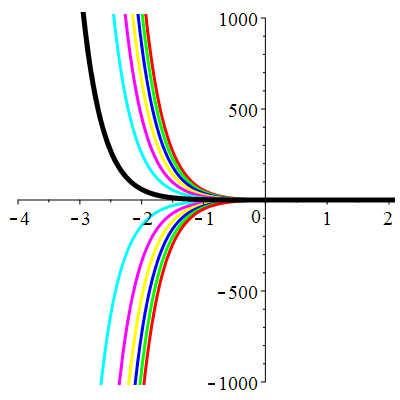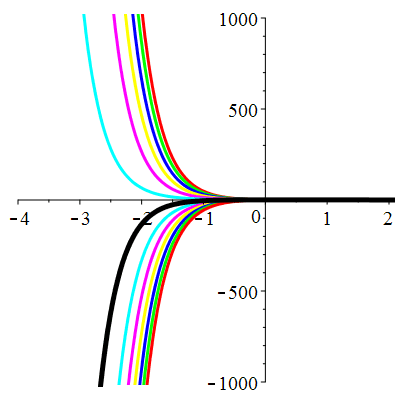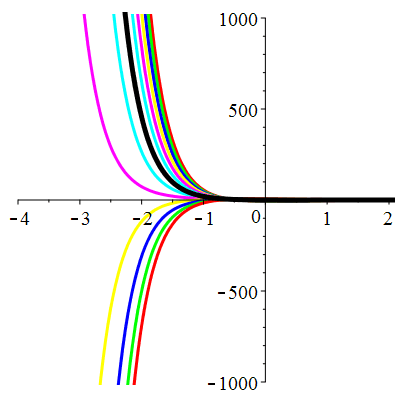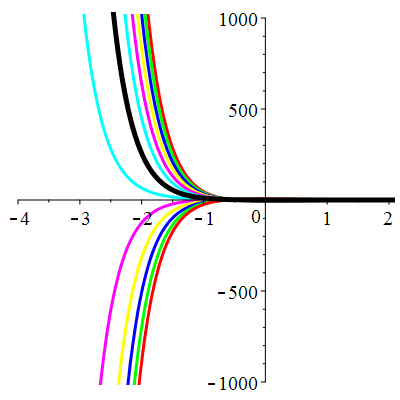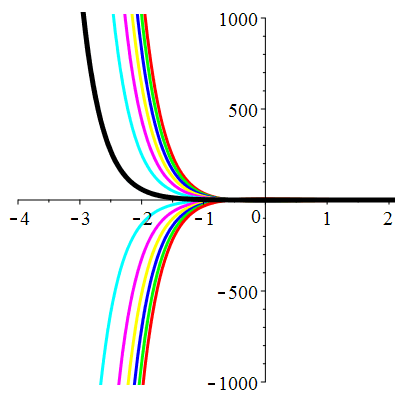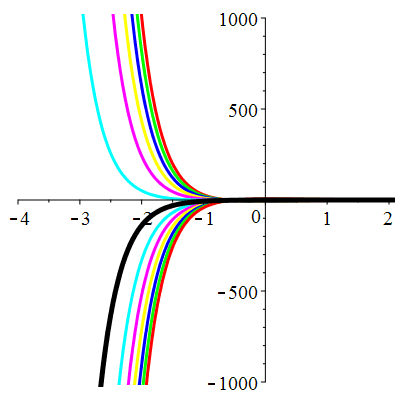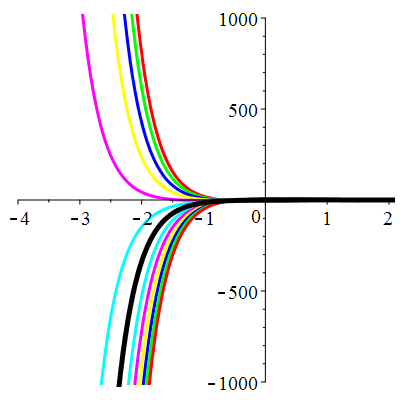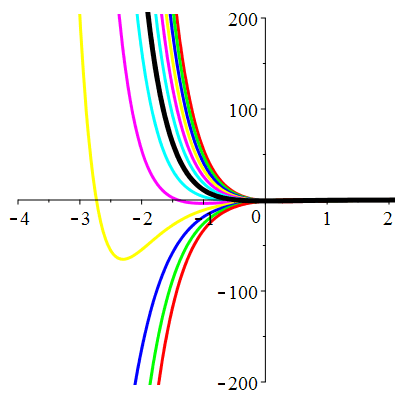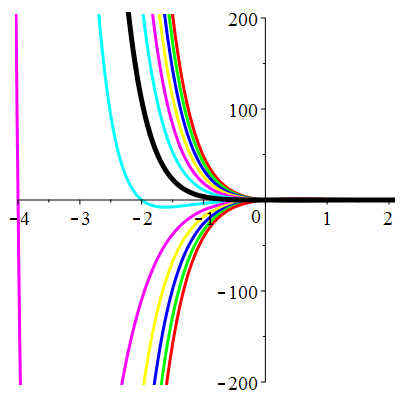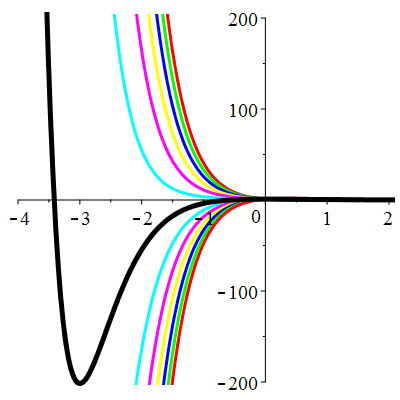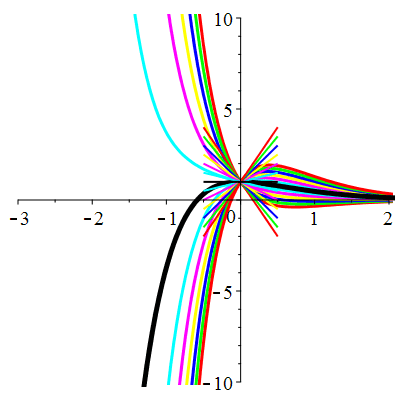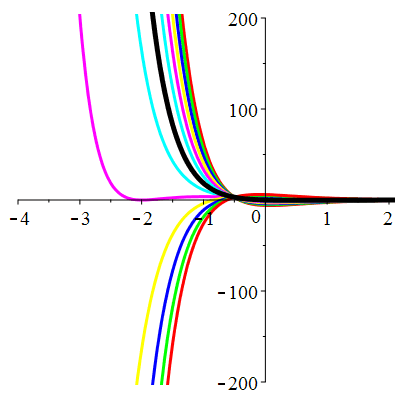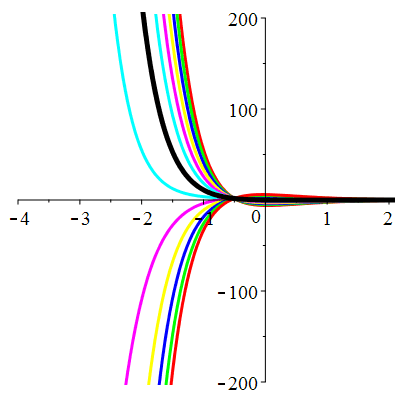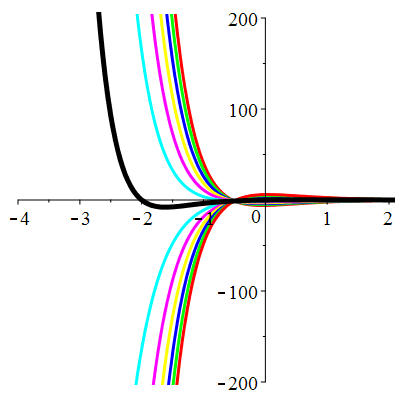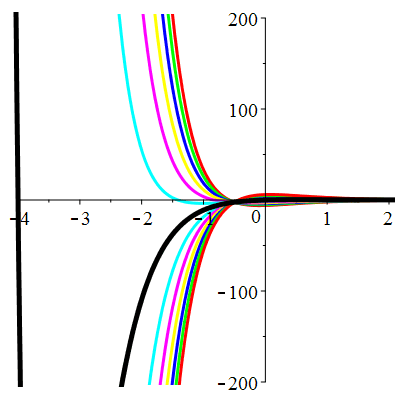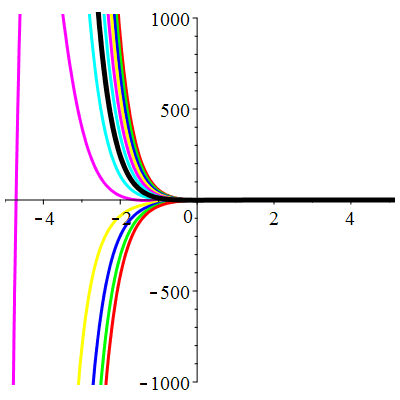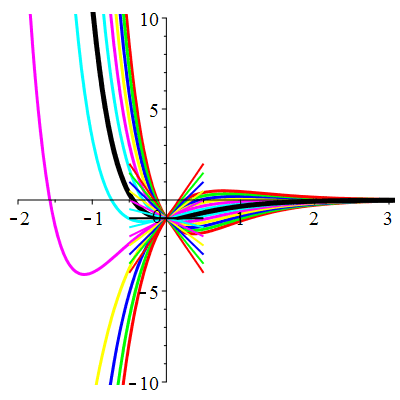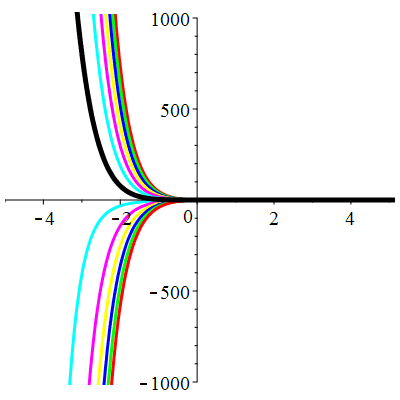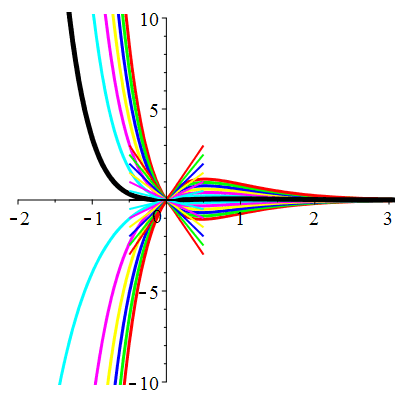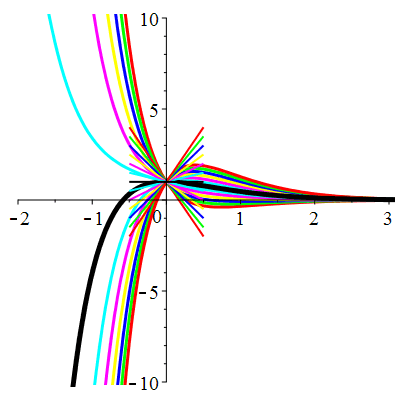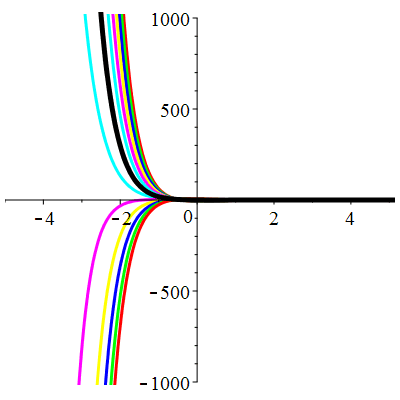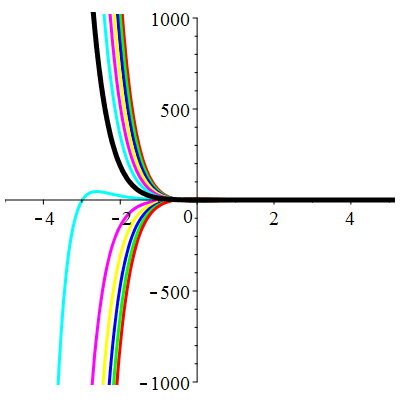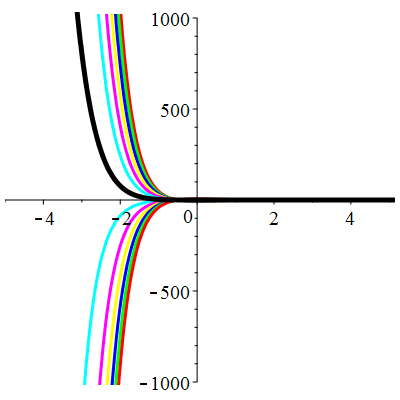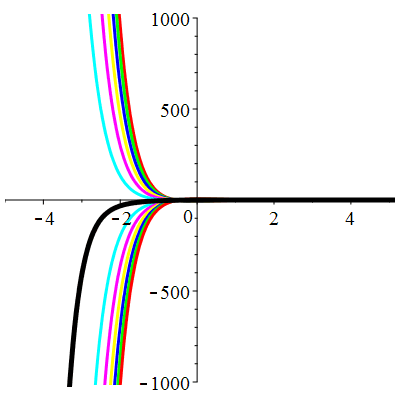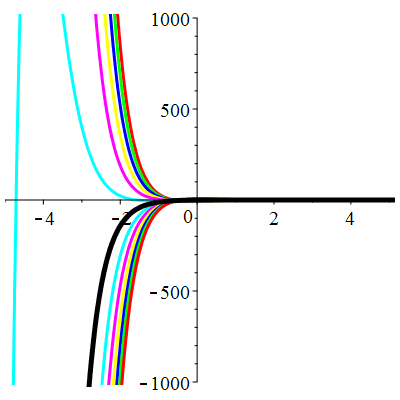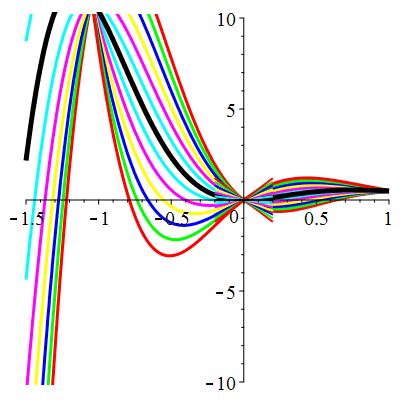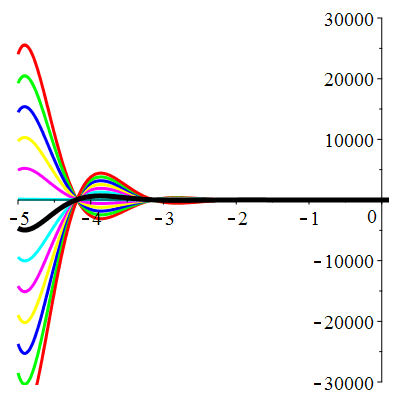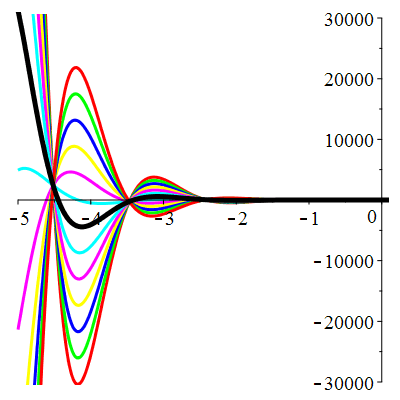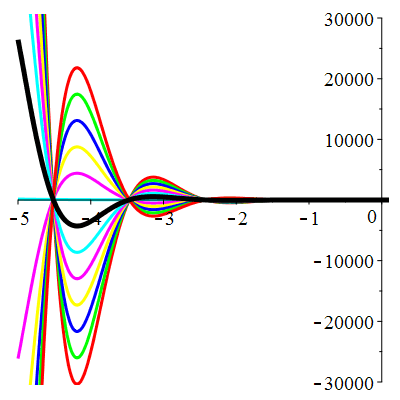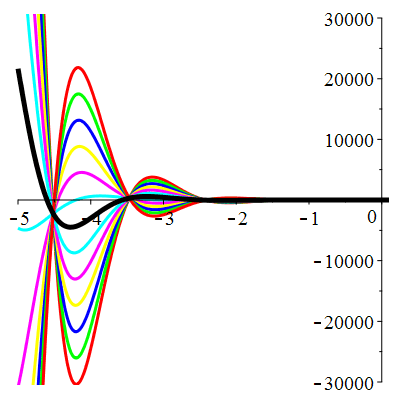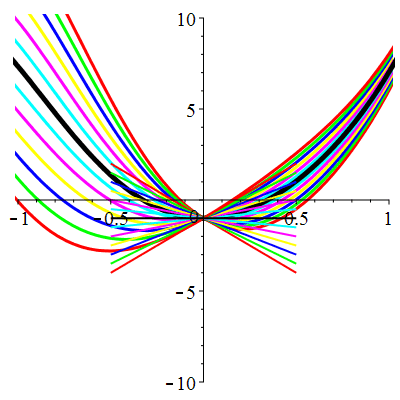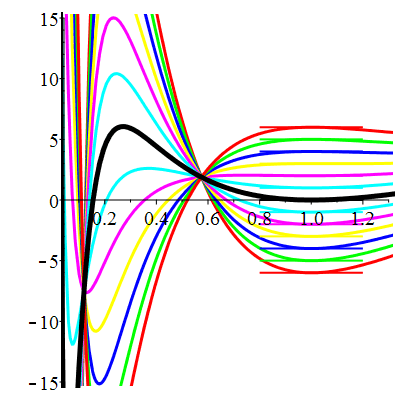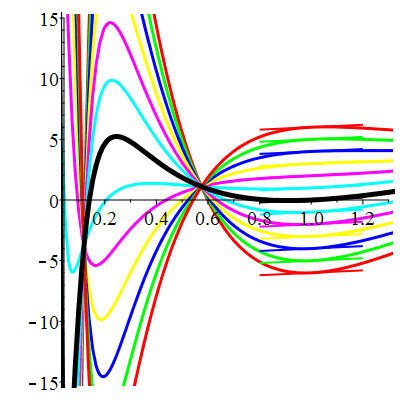III. Équations différentielles
linéaires du 2e ordre
à coefficients constants |
Résolution de \(\ddot{u}(t)+a\dot{u}(t)+bu(t)=\varphi(t)\)
et tracé des courbes intégrales
Solution générale
Hypothèse : \(a,b\!\in\!\mathbb{R}\) et \(\varphi\) est une fonction continue
sur l'intervalle \(I\) à valeurs réelles ou complexes. On fixe un \(t_0\!\in\! I\).
Notations :
- Équation initiale : \((E)\quad\ddot{u}(t)+a\dot{u}(t)+bu(t)=\varphi(t)\)
- Équation homogène associée : \((EH)\quad\ddot{u}(t)+a\dot{u}(t)+bu(t)=0\)
- Équation caractéristique associée : \((EC)\quad r^2+ar+b=0\)
Résolution de \((EH)\):
\(u_{_H}(t)\!=\begin{cases}
\lower -3ex %\vphantom{\dfrac aa}
\!\lambda\,e^{r_1t}\!+\!\mu\,e^{r_2t},\;\lambda,\mu\!\in\!\mathbb{R}
\\
\scriptstyle\text{si \((EC)\) admet deux racines r\(\mathrm{\acute{e}}\)elles distinctes \(r_1\) et \(r_2\)}
\\[1ex]
(\lambda\,t\!+\!\mu)e^{rt},\;\lambda,\mu\!\in\!\mathbb{R}
\\
\scriptstyle\text{si \((EC)\) admet une racine double \(r\)}
\\[1ex]
e^{\rho t}\big(\lambda\cos(\sigma t)\!+\!\mu\sin(\sigma t)\big),\;\lambda,\mu\!\in\!\mathbb{R}
\\
\scriptstyle\text{si \((EC)\) admet deux racines complexes non r\(\mathrm{\acute{e}}\)elles \(\rho+\mathrm{i}\sigma\) et \(\rho-\mathrm{i}\sigma\)}
\end{cases}\)
Résolution de \((E)\): \(u\!=\!u_{_H}\!+u_{_P}\) où
- \(u_{_H}\) est la solution générale de \((EH)~;\)
- \(u_{_P}\) est une solution particulière de \((E)~:\)
\(u_{_P}(t)\!=\!\int_{t_0}^t \varphi(s)G(t-s)\,\mathrm{d}s\) où
\(G(z)=\begin{cases}\vphantom{\dfrac{b^{b^{b^b}}}{a}}
\dfrac{\mathrm{e}^{r_1z}-\mathrm{e}^{r_2z}}{r_1-r_2}
\\
\scriptstyle\text{si \((EC)\) admet deux racines r\(\mathrm{\acute{e}}\)elles distinctes \(r_1\) et \(r_2\)}
\\[1ex] %\vphantom{\dfrac aa}
z\,\mathrm{e}^{rz}
\\
\scriptstyle\text{si \((EC)\) admet une racine double \(r\)}
\\[1ex]
\mathrm{e}^{\rho z}\dfrac{\sin{\sigma z}}{\sigma}
\\
\scriptstyle\text{si \((EC)\) admet deux racines complexes non r\(\mathrm{\acute{e}}\)elles \(\rho+\mathrm{i}\sigma\) et \(\rho-\mathrm{i}\sigma\)}
\end{cases}\)
|
\(u(t)\!=\!u_{_H}(t)\!+\!\int_{t_0}^t \varphi(s)G(t-s)\,\mathrm{d}s\)
|
Cas particulier :
-
Cas d'un second membre de type « polynôme-exponentiel » :
\(\varphi(t)=P(t)\mathrm{e}^{\alpha t}\) où \(P\) est
un polynôme de degré \(d\!\in\!\mathbb{N}\)
à coefficients réels ou complexes
et \(\alpha\!\in\!\mathbb{R}\) ou \(\mathbb{C}.\)
Il existe une solution particulière de la forme
- \(u_{_P}(t)=Q(t)\mathrm{e}^{\alpha t}\) si \(\alpha\) n'est pas racine de \((EC),\)
- \(u_{_P}(t)=tQ(t)\mathrm{e}^{\alpha t}\) si \(\alpha\) est racine simple de \((EC)\) (cas de « résonance simple»),
- \(u_{_P}(t)=t^2Q(t)\mathrm{e}^{\alpha t}\) si \(\alpha\) est racine double de \((EC)\) (cas de « résonance double»),
où \(Q\) est un polynôme de degré \(d.\)
Sous-cas particuliers :
-
Cas d'un second membre polynomial de degré \(d\!\in\!\mathbb{N}:\)
il existe une solution particulière polynomiale
- de degré \(d\) si \(a,b\neq 0~;\)
- de degré \(d+1\) si \(a\neq0\) et \(b=0~;\)
- de degré \(d+2\) si \(a=b=0.\)
-
Cas d'un second membre exponentiel : \(\varphi(t)=A\,\mathrm{e}^{\alpha t}\)
où \(A\!\in\!\mathbb{R}\) ou \(\mathbb{C}.\)
Une solution particulière est donnée par
- \(u_{_P}(t)=\frac{A}{\alpha^2+a\alpha+b}\,\mathrm{e}^{\alpha t}\) si \(\alpha\) n'est pas racine de \((EC)\) ;
- \(u_{_P}(t)=\frac{A}{2\alpha+a}t\,\mathrm{e}^{\alpha t}\) si \(\alpha\) est racine simple de \((EC)\) (cas de « résonance simple ») ;
- \(u_{_P}(t)=\frac{A}{2}t^2\,\mathrm{e}^{\alpha t}\) si \(\alpha\) est racine double de \((EC)\) (cas de « résonance double»).
-
Cas d'un second membre trigonométrique : \(\varphi(t)=A\,\cos(\omega t)+B\,\sin(\omega t)\)
où \(A,B\!\in\!\mathbb{R}\) et \(\omega\!\in\!\mathbb{R}^*.\)
Une solution particulière est donnée par
-
\(u_{_P}(t)=A\,\Re \mathrm{e}\left(\frac{1}{(b-\omega^2)+\mathrm{i}a\omega}\,\mathrm{e}^{\mathrm{i}\omega t}\right)
+B\,\Im \mathrm{m}\left(\frac{1}{(b-\omega^2)+\mathrm{i}a\omega}\,\mathrm{e}^{\mathrm{i}\omega t}\right)\)
\(\phantom{u_{_P}(t)}=\frac{A(b-\omega^2)-Ba\omega}{(\omega^2-b)^2+a^2\omega^2}\cos(\omega t)+\frac{Aa\omega+B(b-\omega^2)}{(\omega^2-b)^2+a^2\omega^2}\sin(\omega t).\)
Principe de superposition :
si \(u_1\) (resp. \(u_2\)) est solution de \(\ddot{u}(t)+a\dot{u}(t)+bu(t)=\varphi_1(t)\)
(resp. \(\ddot{u}(t)+a\dot{u}(t)+bu(t)=\varphi_2(t)\)), alors
\(\alpha_1u_1\!+\!\alpha_2u_2\) est solution de \(\ddot{u}(t)+a\dot{u}(t)+bu(t)=\alpha_1\varphi_1(t)\!+\!\alpha_2\varphi_2(t)\).
Problème de Cauchy :
on fixe un \(t_0\!\in\! I\) ainsi que \(u_0,v_0\!\in\!\mathbb{R}.\)
L'équation \((E)\) admet une unique solution vérifiant \(u(t_0)\!=u_0\) et \(\dot{u}(t_0)\!=v_0.\)
Elle est donnée par
|
\(u(t)=u_0H(t-t_0)+v_0G(t-t_0)+u_{_P}(t)\)
|
où \(u_{_P}(t)\!=\!\int_{t_0}^t \varphi(s)G(t-s)\,\mathrm{d}s\) et
\(\begin{cases}\vphantom{\dfrac{b^{b^{b^b}}}{a}}
G(z)=\dfrac{\mathrm{e}^{r_1z}-\mathrm{e}^{r_2z}}{r_1-r_2}
\hspace{2em}
H(z)=\dfrac{r_2\mathrm{e}^{r_1z}-r_1\mathrm{e}^{r_2z}}{r_2-r_1}
\\
\scriptstyle\text{si \((EC)\) admet deux racines r\(\mathrm{\acute{e}}\)elles distinctes \(r_1\) et \(r_2\)}
\\[1ex] %\vphantom{\dfrac aa}
G(z)=z\,\mathrm{e}^{rz}
\hspace{4.3em}
H(z)=(1-rz)\,\mathrm{e}^{rz}
\\
\scriptstyle\text{si \((EC)\) admet une racine double \(r\)}
\\[1ex]
G(z)=\hspace{0em}\mathrm{e}^{\rho z}\dfrac{\sin{\sigma z}}{\sigma}
\hspace{2em}
H(z)=\hspace{0em}\mathrm{e}^{\rho z}\left(\cos(\sigma z)-\dfrac{\rho}{\sigma}\sin(\sigma z)\right)
\\
\scriptstyle\text{si \((EC)\) admet deux racines complexes non r\(\mathrm{\acute{e}}\)elles \(\rho+\mathrm{i}\sigma\) et \(\rho-\mathrm{i}\sigma\)}
\end{cases}\)
On a \(\big[u_{_P}(t_0)=\hspace{0em} \dot{u}_{_P}(t_0)=0\big],\)
\(\big[G(t_0)=0,\dot{G}(t_0)=1\big]\)
et \(\big[(H(t_0)=1,\dot{H}(t_0)=0\big].\)
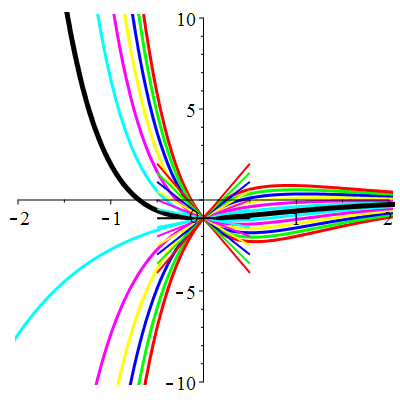
\(\vphantom{()_p^b}\) \(a=3\qquad b=2\qquad \varphi(t)=0\)
| Solution : |
\(u(t)\!=\!\lambda\,\mathrm{e}^{-t}\!+\! \mu\,\mathrm{e}^{-2t}\) |
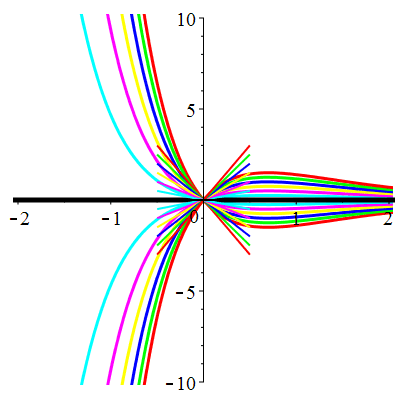
Courbes concourantes en 0
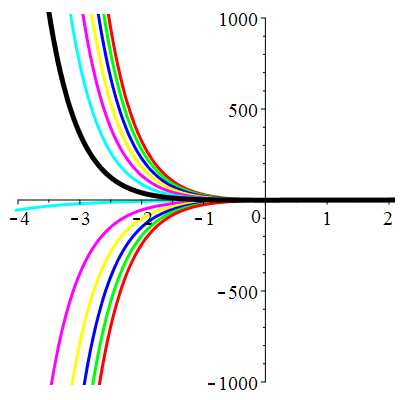
|
|
| \(u(0)=-1\) | Zoom |
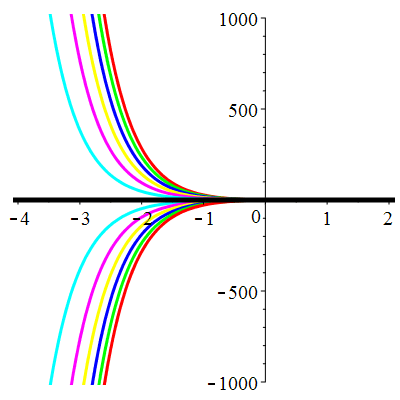
|
|
| \(u(0)=0\) | Zoom |
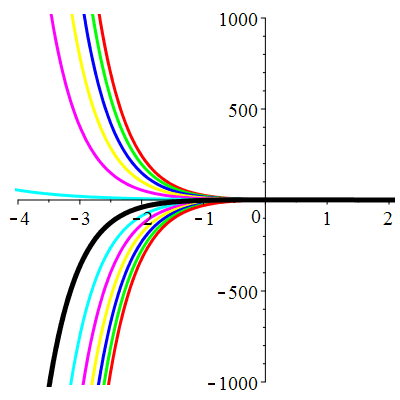
|
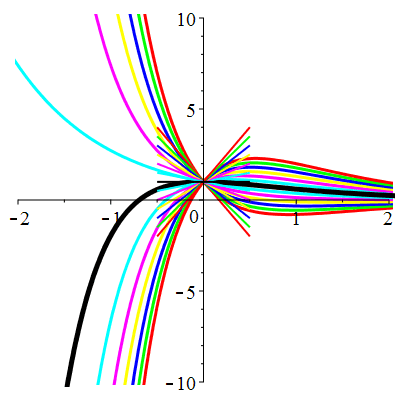
|
| \(u(0)=1\) | Zoom |
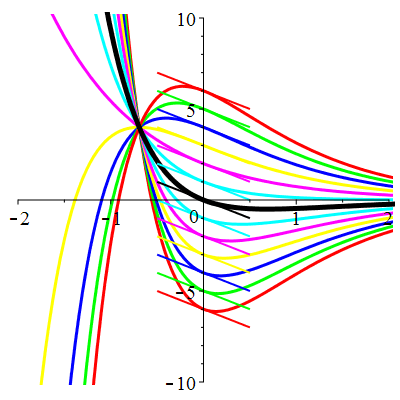
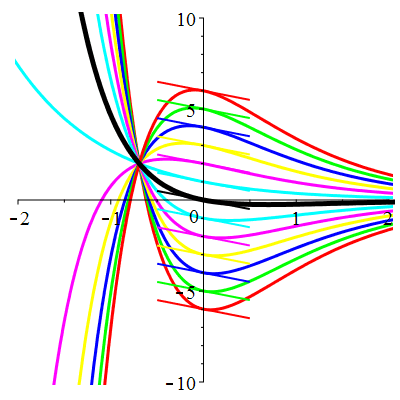
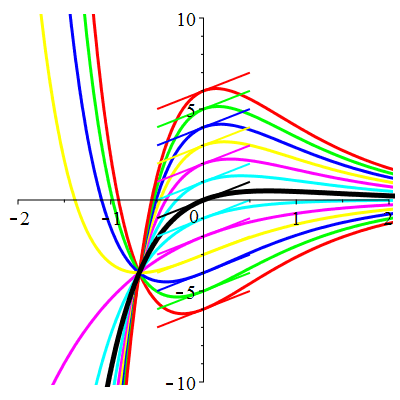
Courbes de pente constante en 0
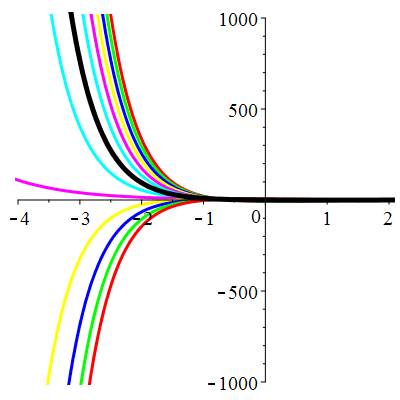
|
|
| \(\dot{u}(0)=-2\) | Zoom |
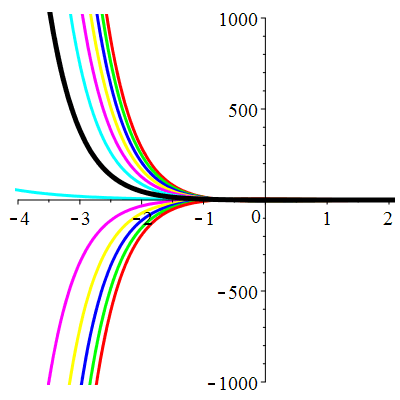
|
|
| \(\dot{u}(0)=-1\) | Zoom |
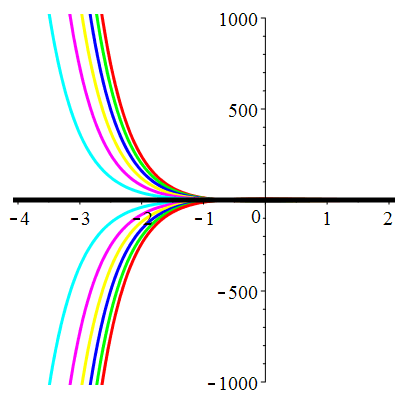
|
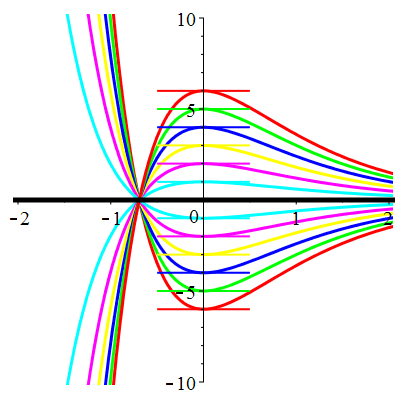
|
| \(\dot{u}(0)=0\) | Zoom |
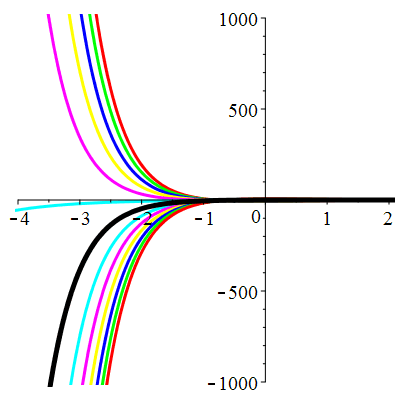
|
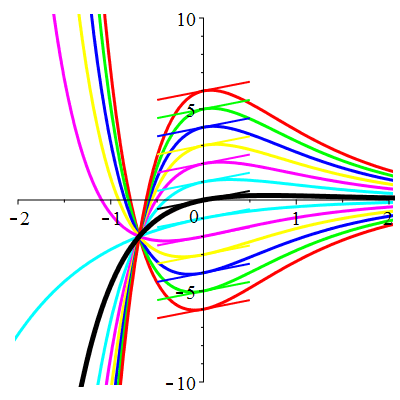
|
| \(\dot{u}(0)=1\) | Zoom |
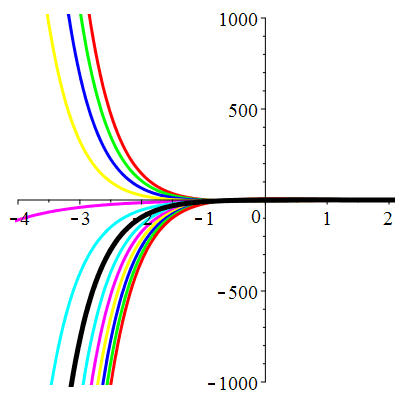
|
|
| \(\dot{u}(0)=2\) | Zoom |
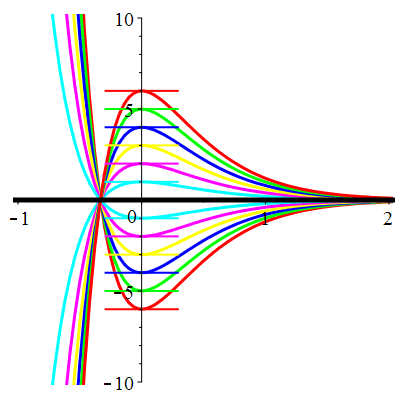
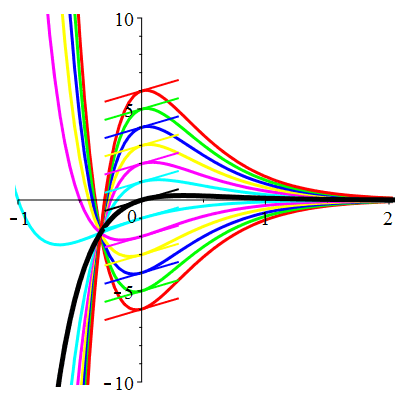
\(\vphantom{()_p^b}\) \(a=6\qquad b=9\qquad \varphi(t)=0\)
| Solution : |
\(u(t)\!=\!(\lambda\,t\!+\!\mu)\mathrm{e}^{-3t}\) |
Courbes concourantes en 0
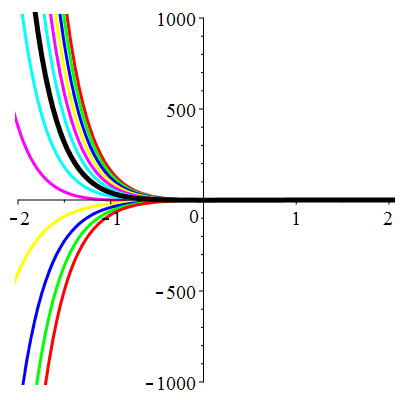
|
|
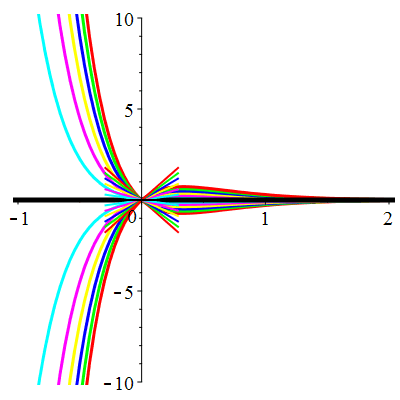
| \(u(0)=-1\) | Zoom |
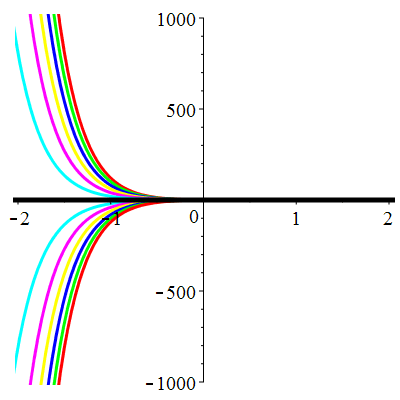
|
|
| \(u(0)=0\) | Zoom |
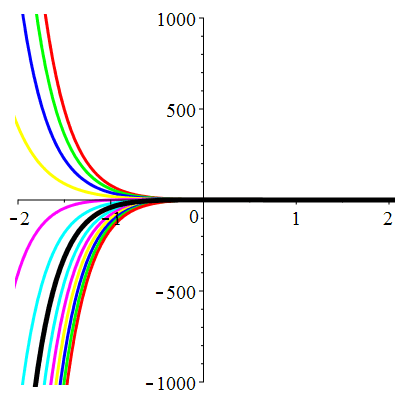
|
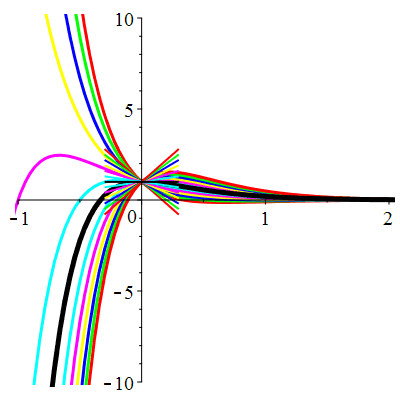
|
| \(u(0)=1\) | Zoom |
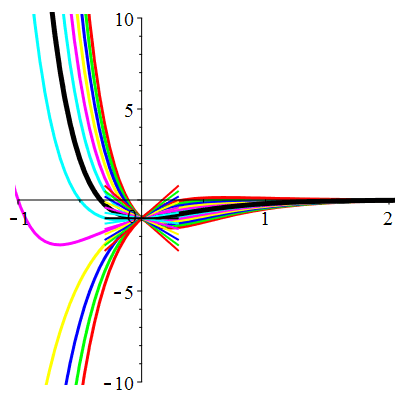
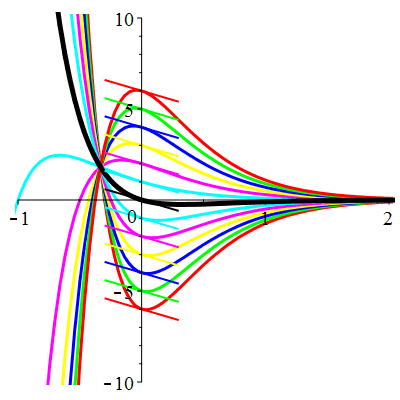
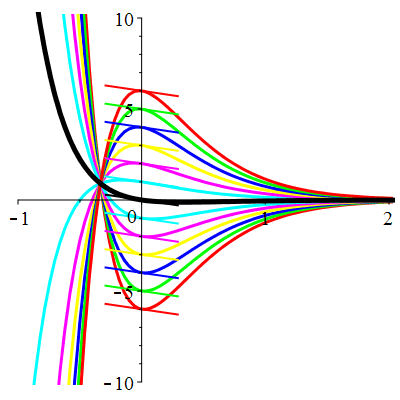
Courbes de pente constante en 0
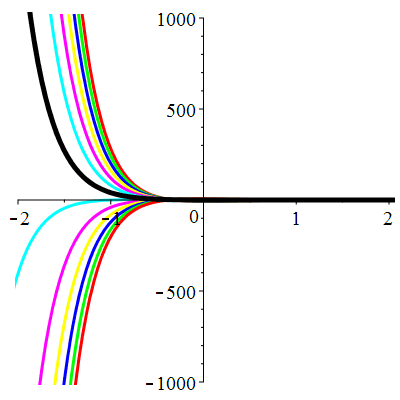
|
|
| \(\dot{u}(0)=-2\) | Zoom |
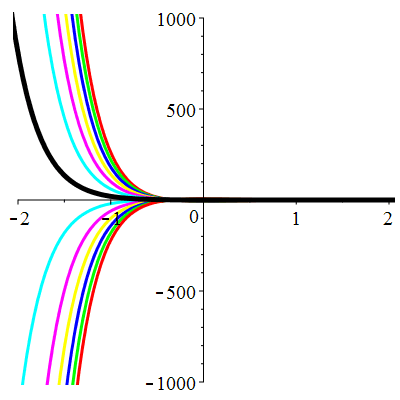
|
|
| \(\dot{u}(0)=-1\) | Zoom |
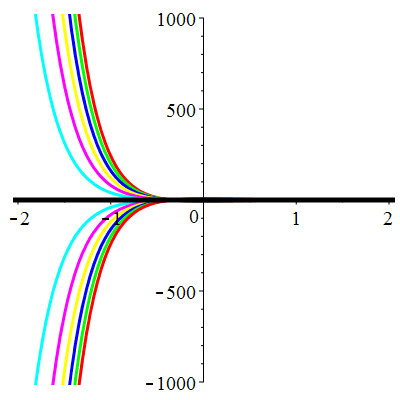
|
|
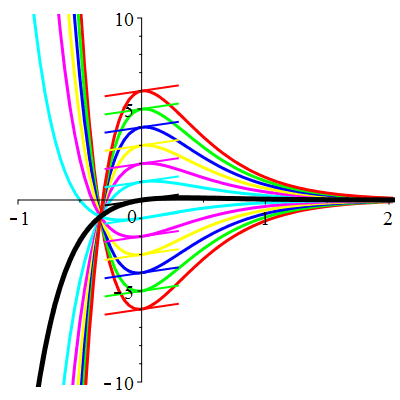
| \(\dot{u}(0)=0\) | Zoom |
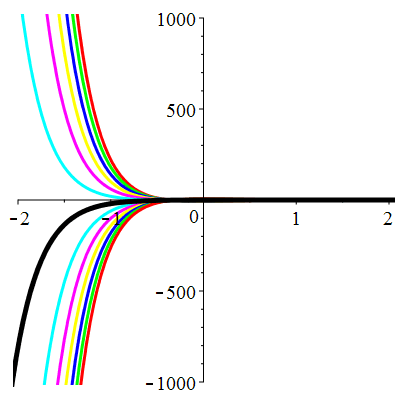
|
|
| \(\dot{u}(0)=1\) | Zoom |
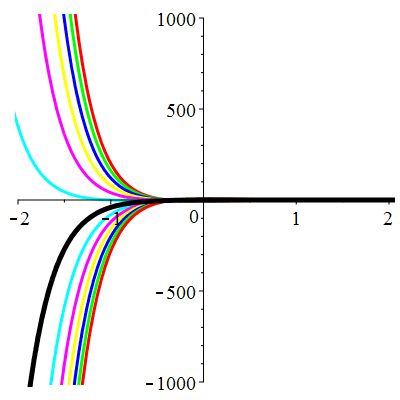
|
|
| \(\dot{u}(0)=2\) | Zoom |
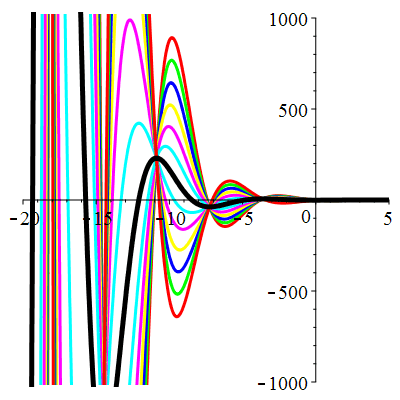
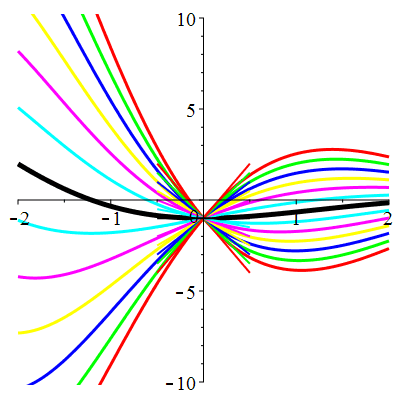
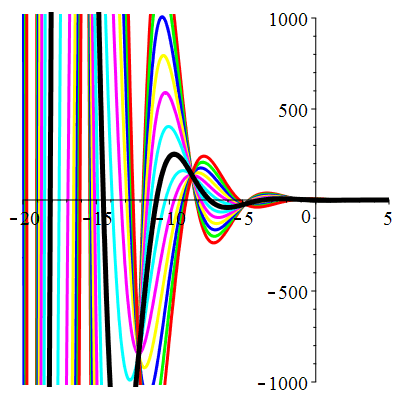
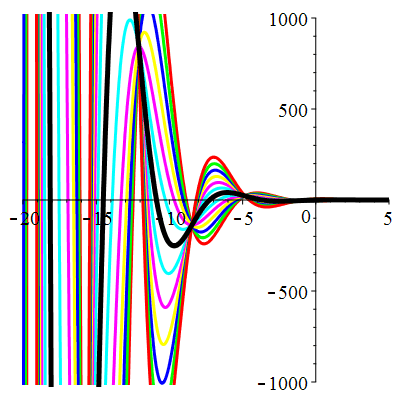
\(\vphantom{()_p^b}\) \(a=1\qquad b=1\qquad \varphi(t)=0\)
| Solution : |
\(u(t)\!=\!\Big[\lambda\cos\!\big(\!\frac{\sqrt{3}}{2}t\big)
\!+\!\mu\sin\!\big(\!\frac{\sqrt{3}}{2}t\big)\Big]\mathrm{e}^{-\frac12 t}\) |
Courbes concourantes en 0
|
|
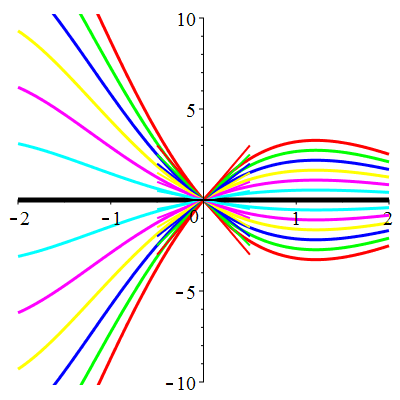
| \(u(0)=-1\) | Zoom |
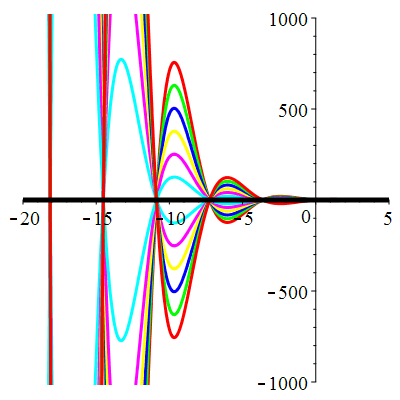
|
|
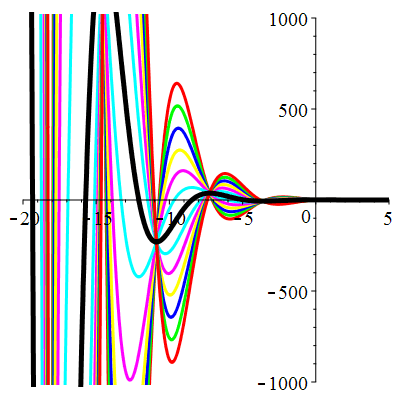
| \(u(0)=0\) | Zoom |
|
|
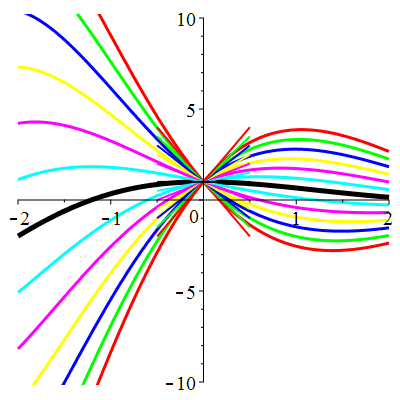
| \(u(0)=1\) | Zoom |
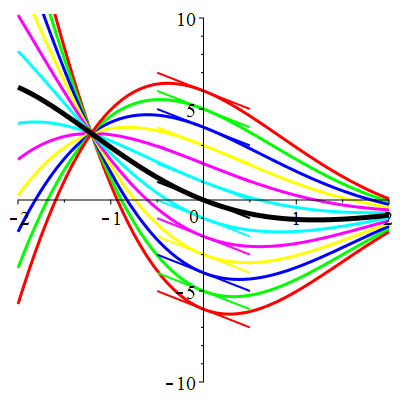
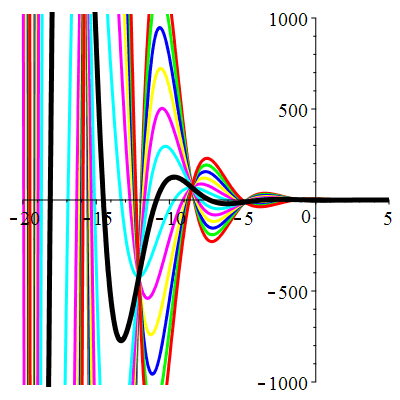
Courbes de pente constante en 0
|
|
| \(\dot{u}(0)=-2\) | Zoom |
|
|
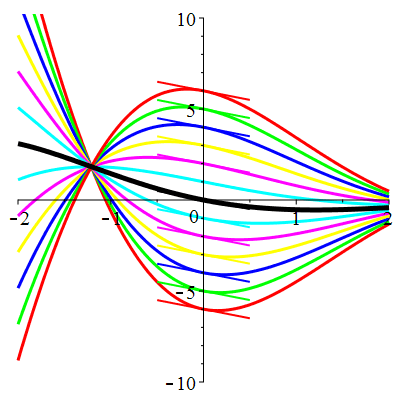
| \(\dot{u}(0)=-1\) | Zoom |
|
|
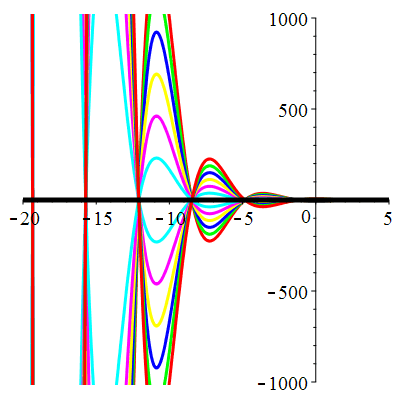
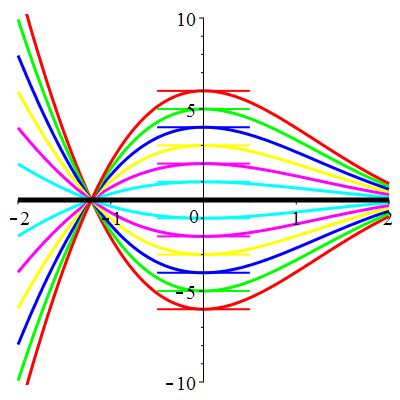
| \(\dot{u}(0)=0\) | Zoom |
|
|
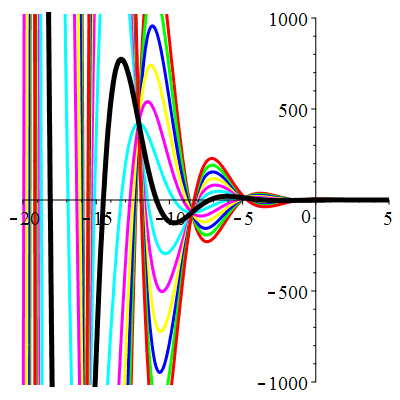
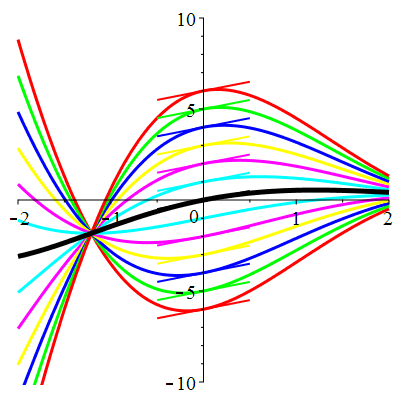
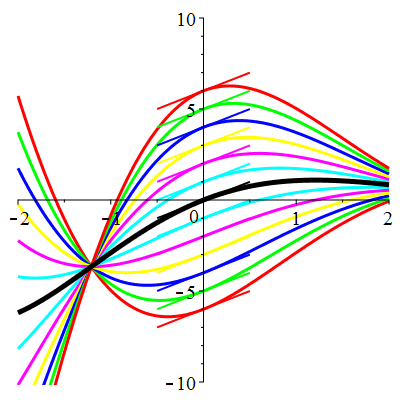
| \(\dot{u}(0)=1\) | Zoom |
|
|
| \(\dot{u}(0)=2\) | Zoom |
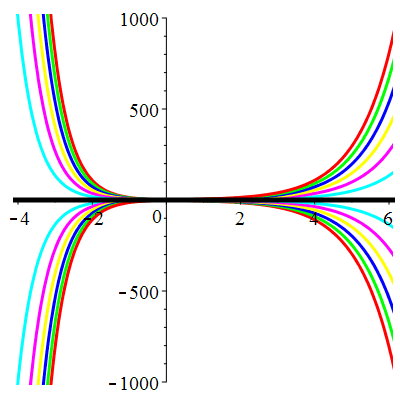
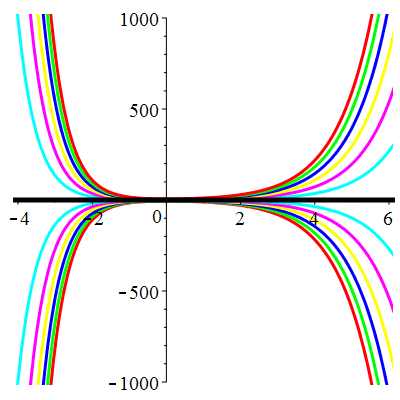
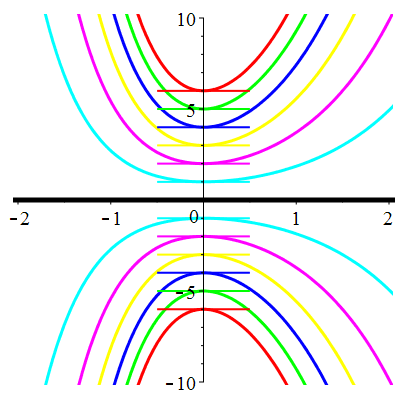
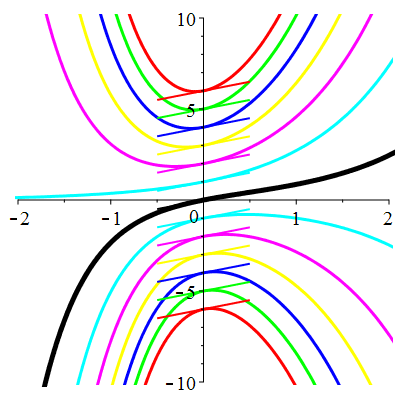
\(\vphantom{()_p^b}\) \(a=1\qquad b=-2\qquad \varphi(t)=0\)
| Solution : |
\(u(t)\!=\!\lambda\,\mathrm{e}^{t}\!+\!\mu\,\mathrm{e}^{-2t}\) |
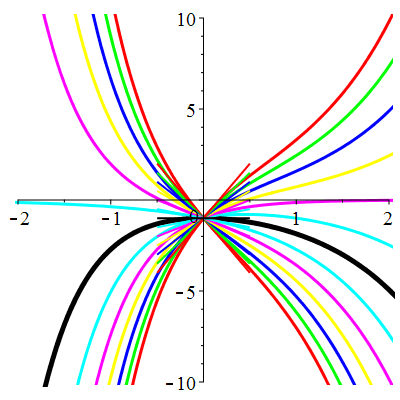
Courbes concourantes en 0
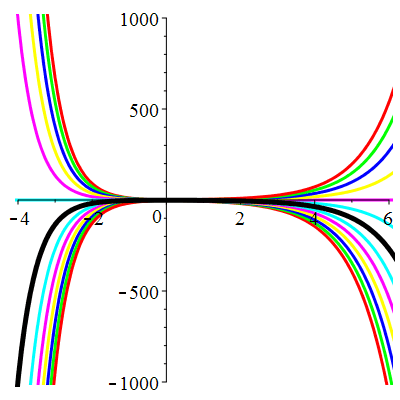
|
|
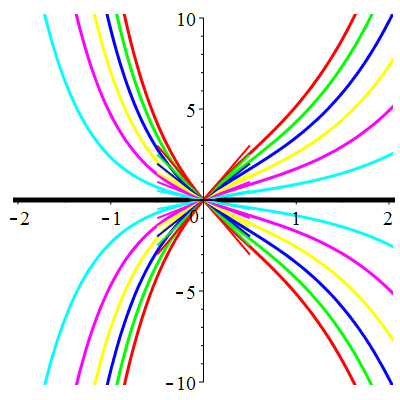
| \(u(0)=-1\) | Zoom |
|
|
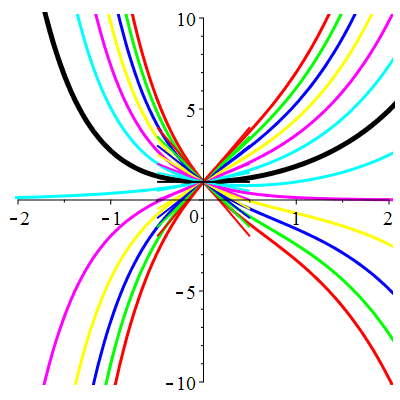
| \(u(0)=0\) | Zoom |
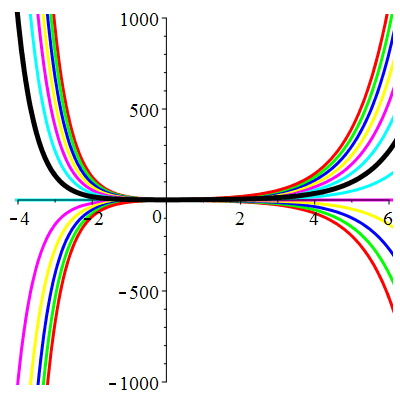
|
|
| \(u(0)=1\) | Zoom |
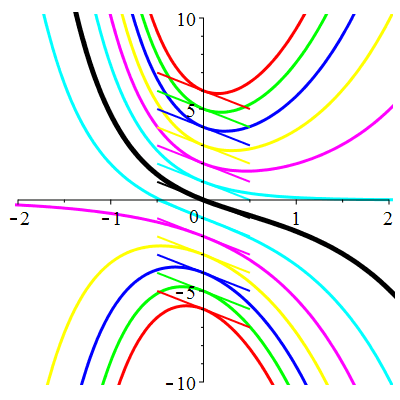
Courbes de pente constante en 0
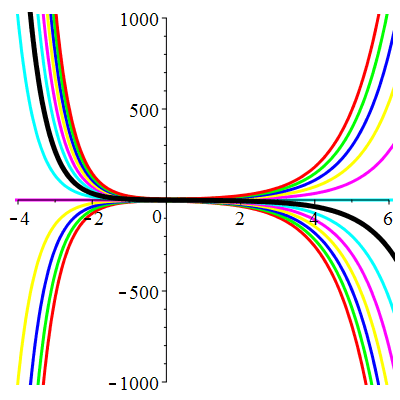
|
|
| \(\dot{u}(0)=-2\) | Zoom |
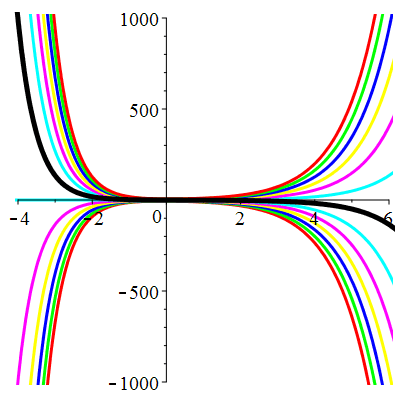
|
|
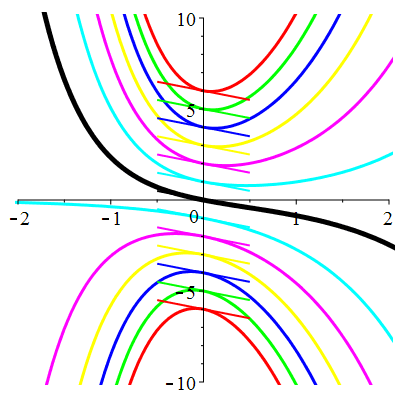
| \(\dot{u}(0)=-1\) | Zoom |
|
|
| \(\dot{u}(0)=0\) | Zoom |
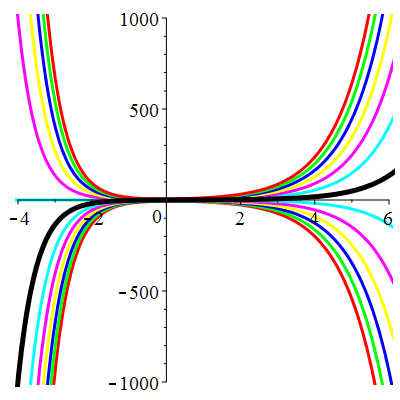
|
|
| \(\dot{u}(0)=1\) | Zoom |
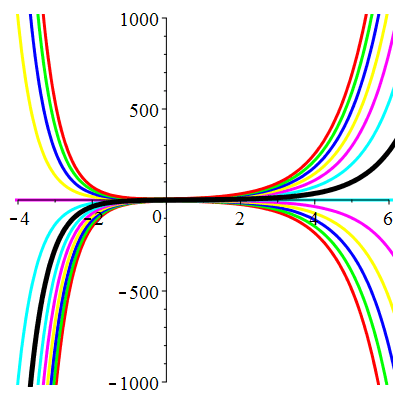
|
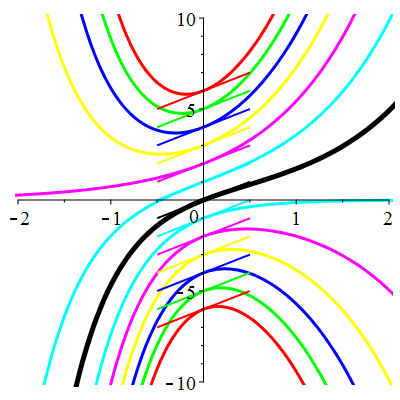
|
| \(\dot{u}(0)=2\) | Zoom |
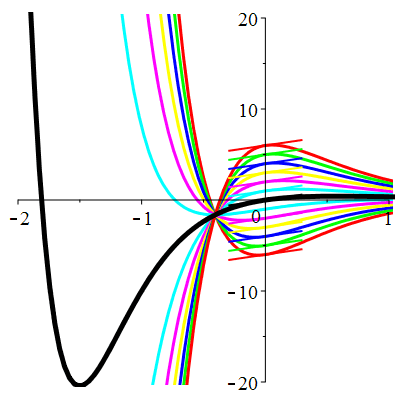
\(\vphantom{()_p^b}\) \(a=5\qquad b=6\qquad \varphi(t)=2\,\mathrm{e}^{-t}+\,\mathrm{e}^{-3t}\)
| Solution : |
\(u(t)\!=\!(\lambda-t)\mathrm{e}^{-3t}\!+\! \mu\,\mathrm{e}^{-2t}\!+\hspace{-0.1em}\mathrm{e}^{-t}\) |
Courbes concourantes en 0

|
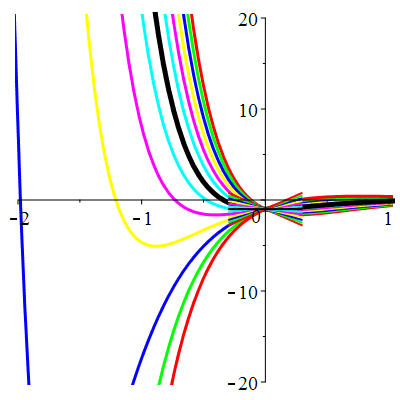
|
| \(u(0)=-1\) | Zoom |
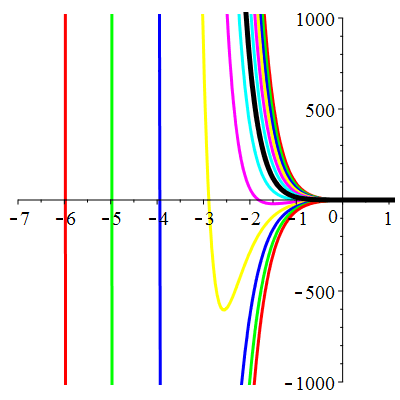
|
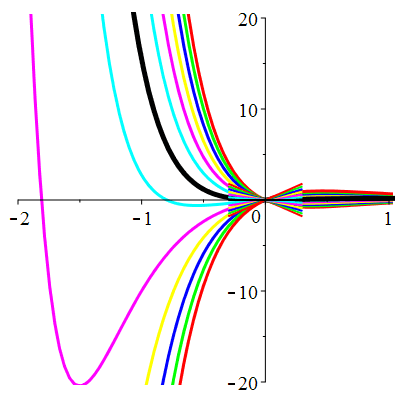
|
| \(u(0)=0\) | Zoom |
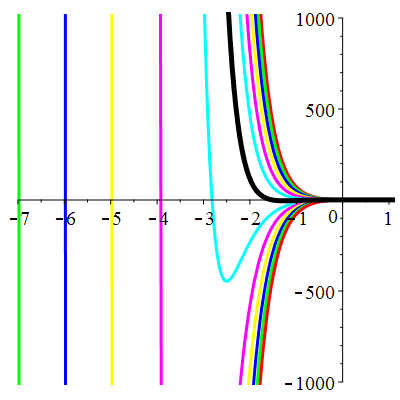
|
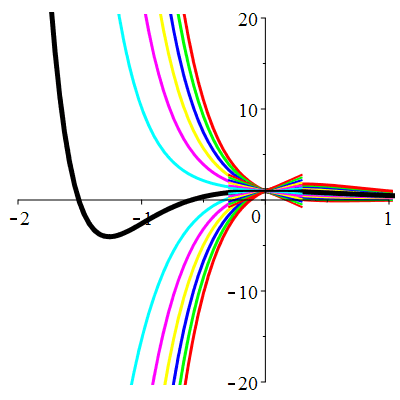
|
| \(u(0)=1\) | Zoom |
Courbes de pente constante en 0
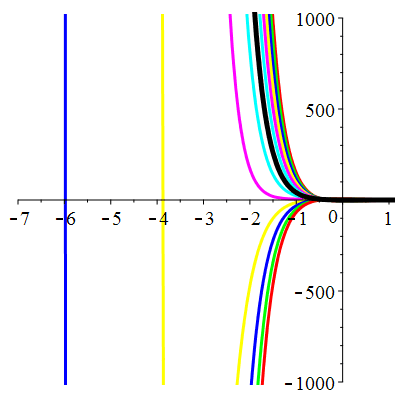
|
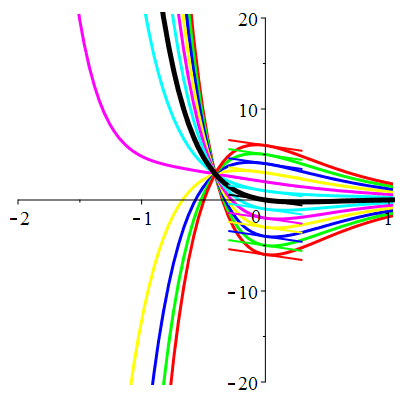
|
| \(\dot{u}(0)=-2\) | Zoom |
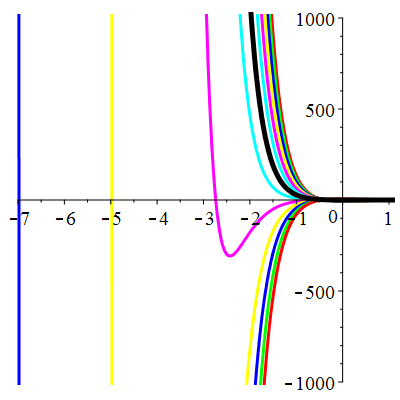
|
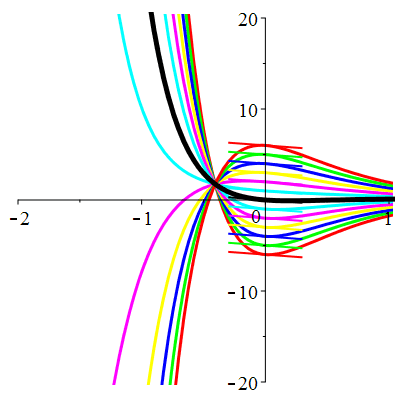
|
| \(\dot{u}(0)=-1\) | Zoom |
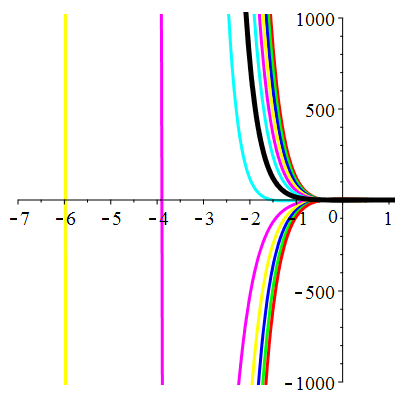
|
|
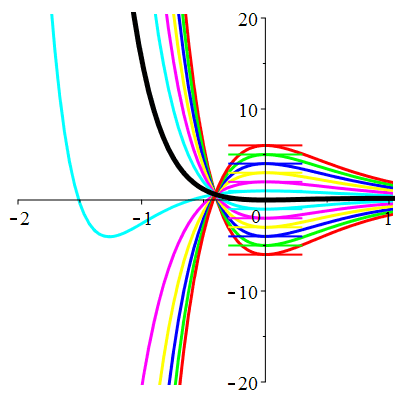
| \(\dot{u}(0)=0\) | Zoom |
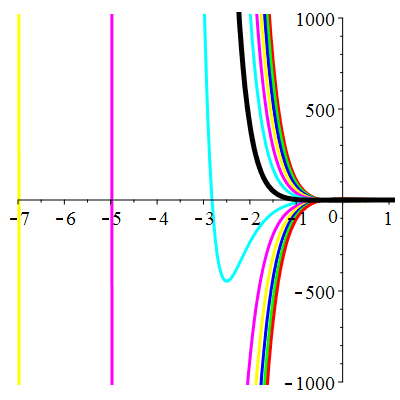
|
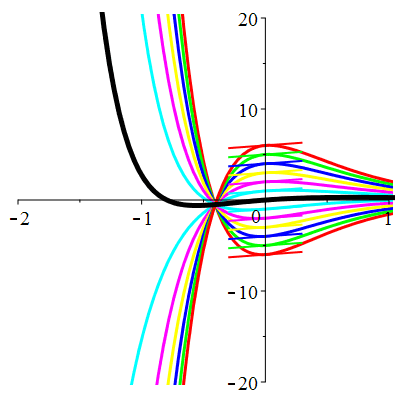
|
| \(\dot{u}(0)=1\) | Zoom |
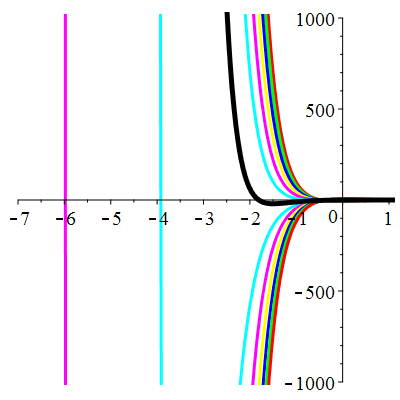
|
|
| \(\dot{u}(0)=2\) | Zoom |
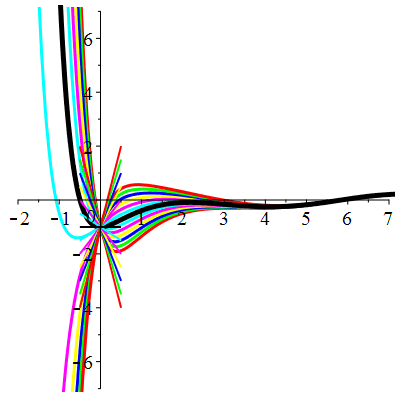
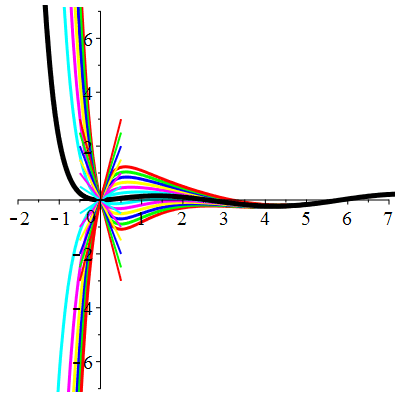
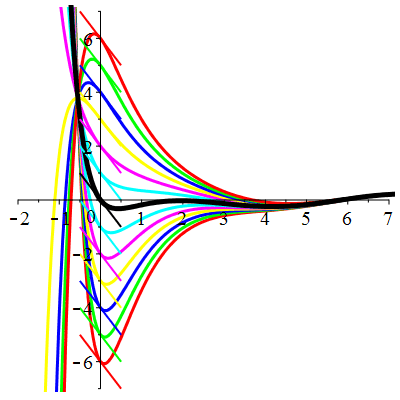
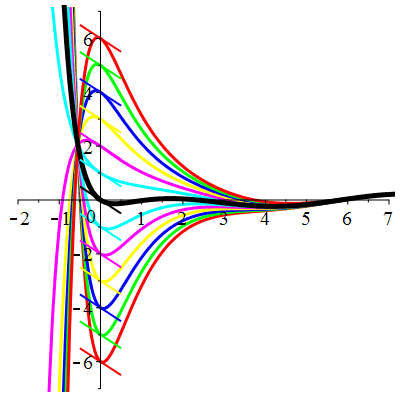
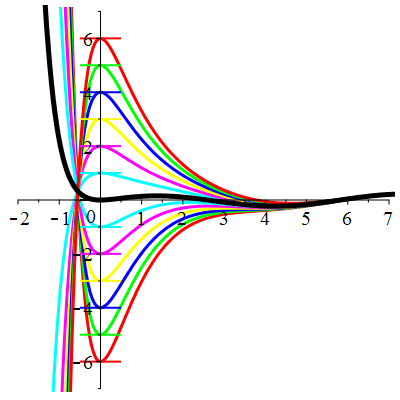
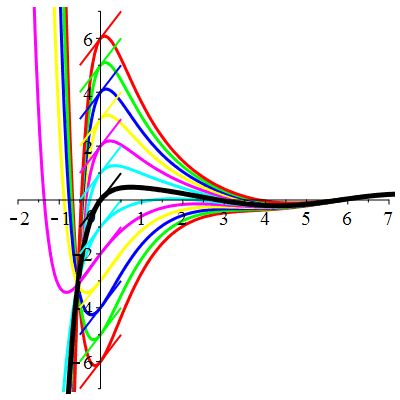
\(\vphantom{()_p^b}\) \(a=4\qquad b=3\qquad \varphi(t)=\cos t\)
| Solution : |
\(u(t)\!=\!\lambda\,\mathrm{e}^{-t}\!+\!\mu\,\mathrm{e}^{-3t}\!+\!\frac{1}{10}\cos t\!+\!\frac15\sin t\) |
Courbes concourantes en 0
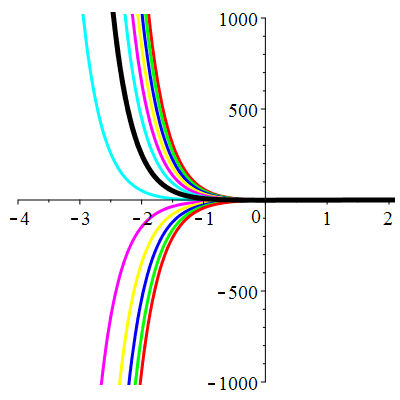
|
|
| \(u(0)=-1\) | Zoom |
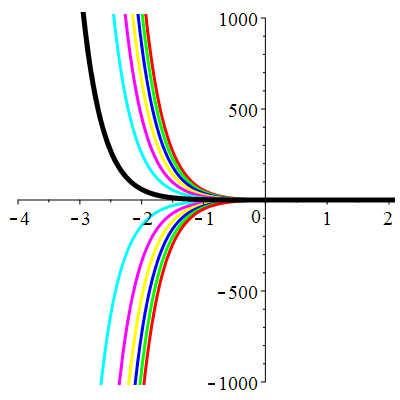
|
|
| \(u(0)=0\) | Zoom |
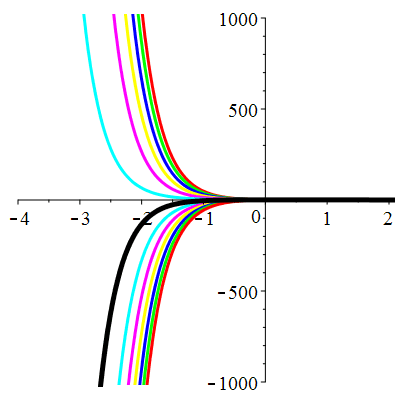
|
|
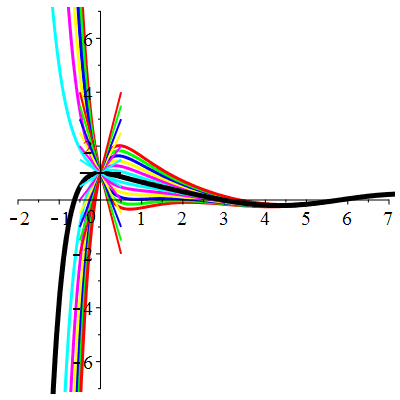
| \(u(0)=1\) | Zoom |
Courbes de pente constante en 0
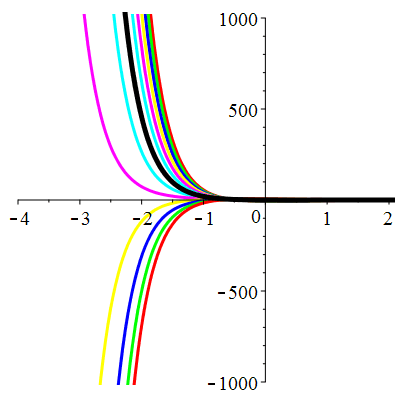
|
|
| \(\dot{u}(0)=-2\) | Zoom |
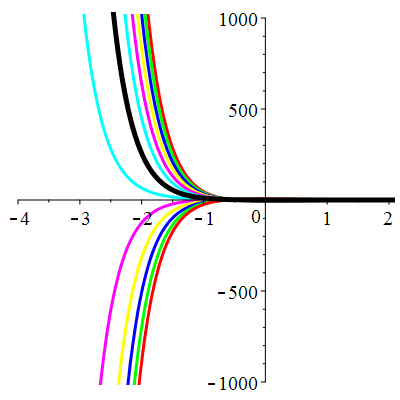
|
|
| \(\dot{u}(0)=-1\) | Zoom |
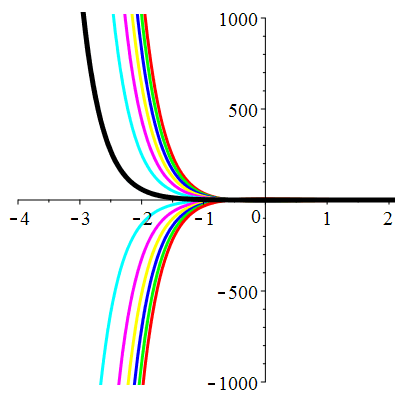
|
|
| \(\dot{u}(0)=0\) | Zoom |
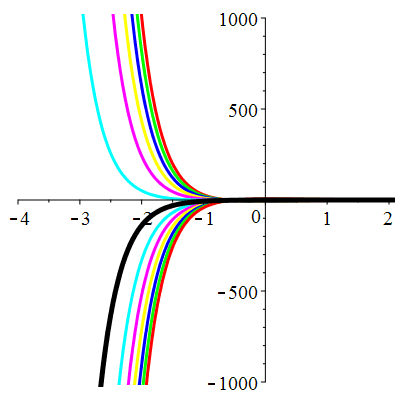
|
|
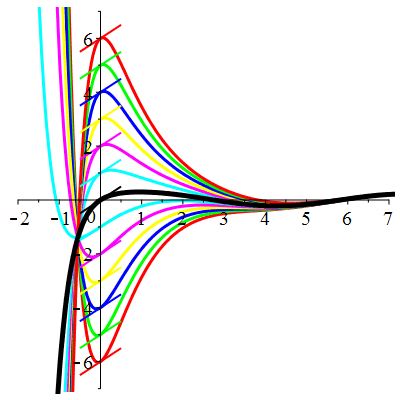
| \(\dot{u}(0)=1\) | Zoom |
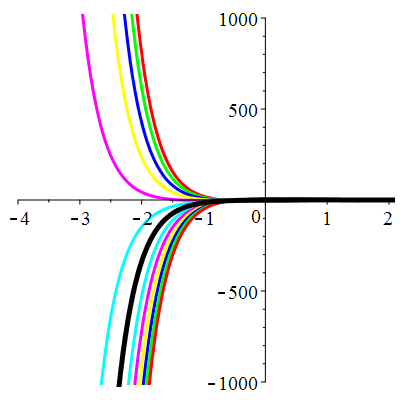
|
|
| \(\dot{u}(0)=2\) | Zoom |
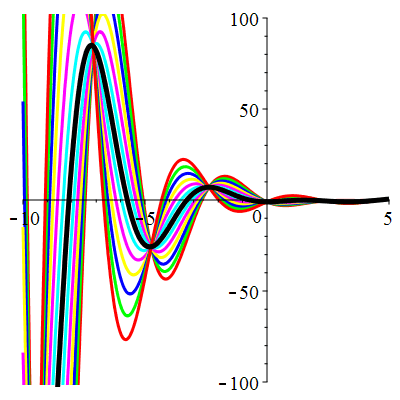
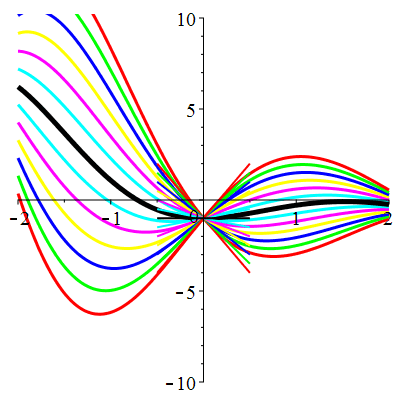
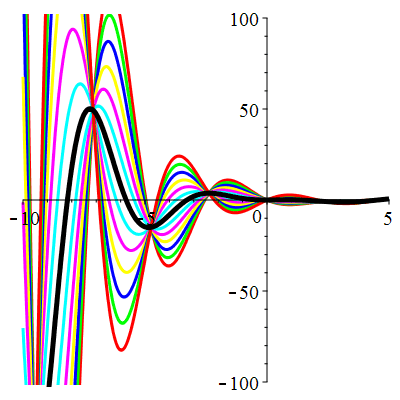
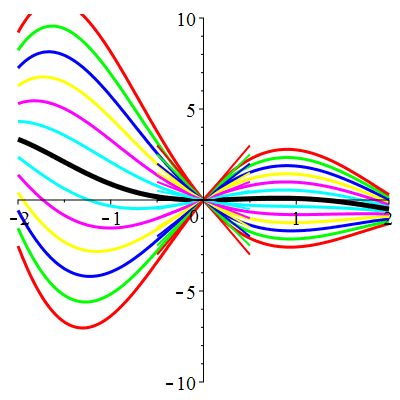
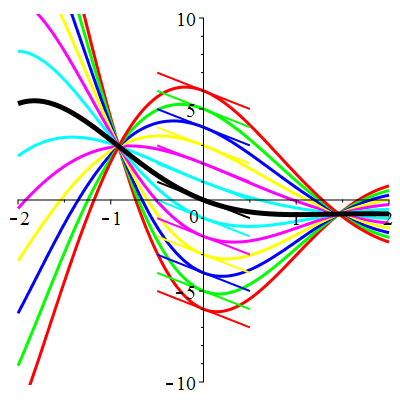
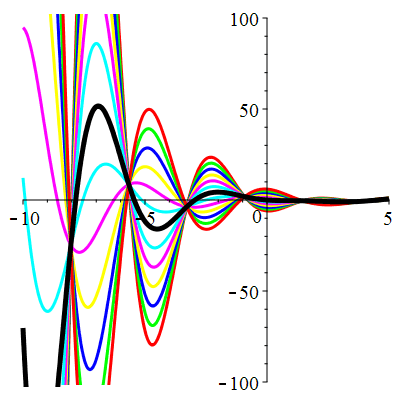
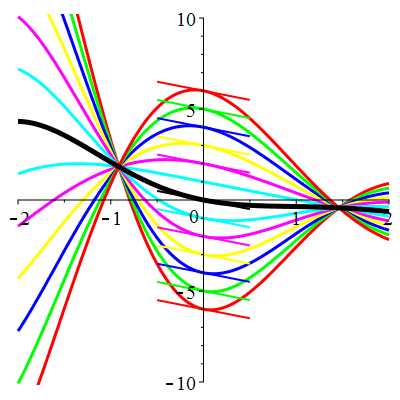
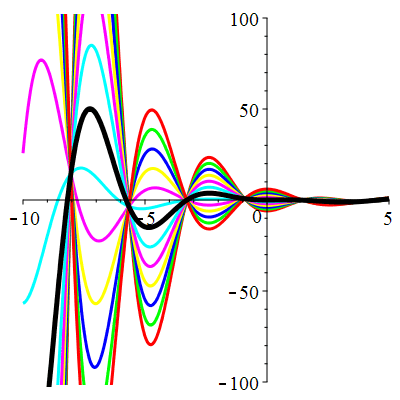
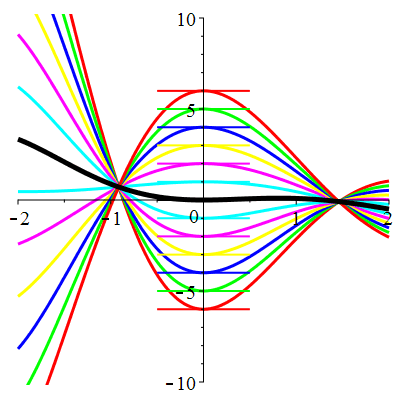
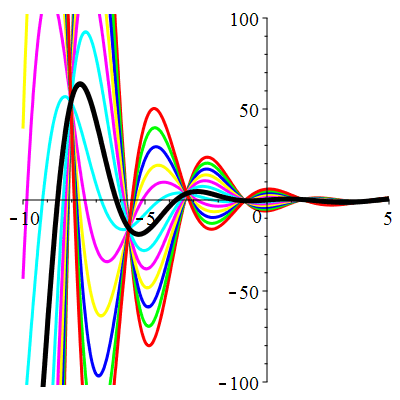
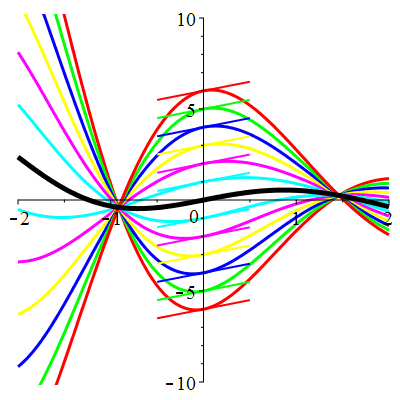
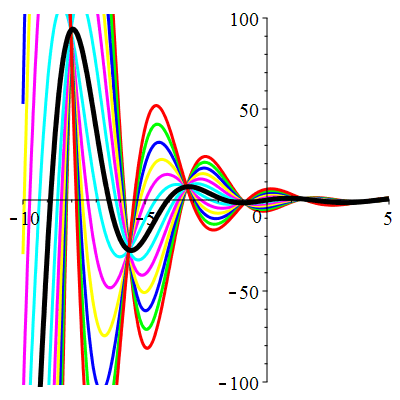
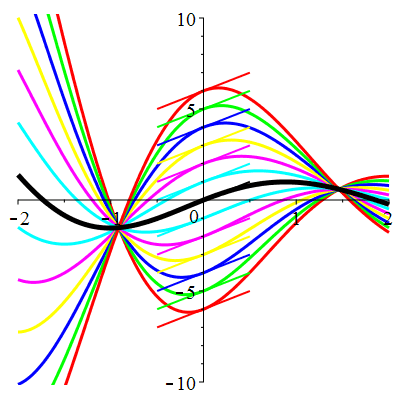
\(\vphantom{()_p^b}\) \(a=1\qquad b=2\qquad \varphi(t)=2\cos\!\big(t\!+\!\frac{\pi}{3}\!\big)\)
| Solution : |
\(u(t)\!=\!\Big[\lambda\cos\!\big(\!\frac{\sqrt{7}}{2}t\big)\!+\!\mu\sin\!\big(\!\frac{\sqrt{7}}{2}t\big)\Big]\mathrm{e}^{-\frac12 t}
\!+\!\sqrt2\cos\!\big(t\!+\!\frac{\pi}{12}\!\big)\) |
Courbes concourantes en 0
|
|
| \(u(0)=-1\) | Zoom |
|
|
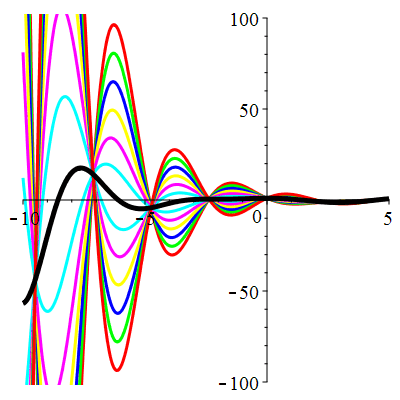
| \(u(0)=0\) | Zoom |
|
|
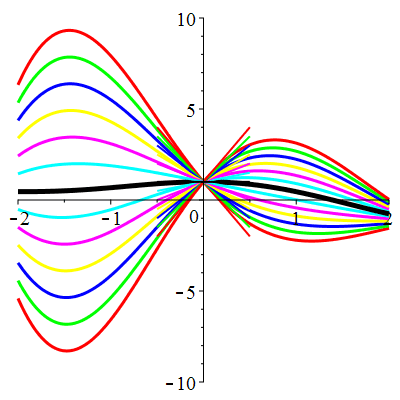
| \(u(0)=1\) | Zoom |
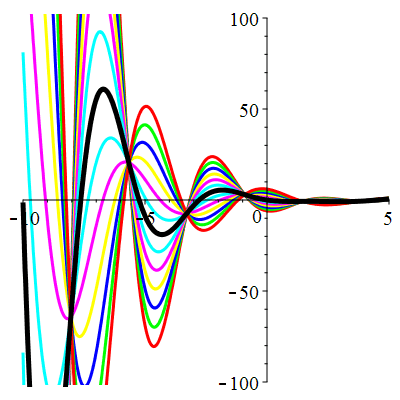
Courbes de pente constante en 0
|
|
| \(\dot{u}(0)=-2\) | Zoom |
|
|
| \(\dot{u}(0)=-1\) | Zoom |
|
|
| \(\dot{u}(0)=0\) | Zoom |
|
|
| \(\dot{u}(0)=1\) | Zoom |
|
|
| \(\dot{u}(0)=2\) | Zoom |
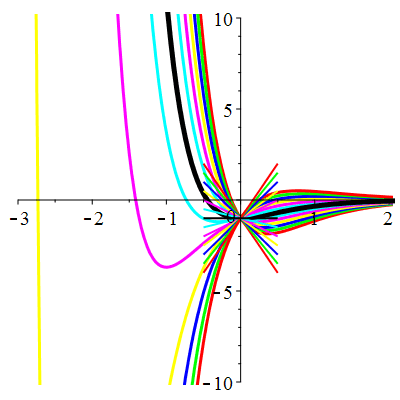
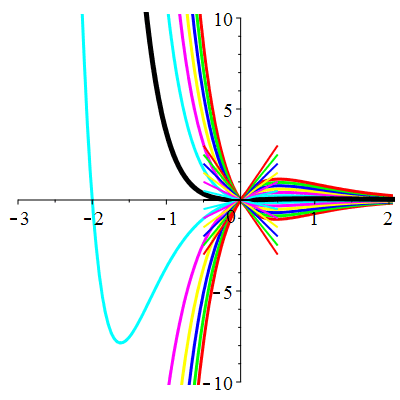
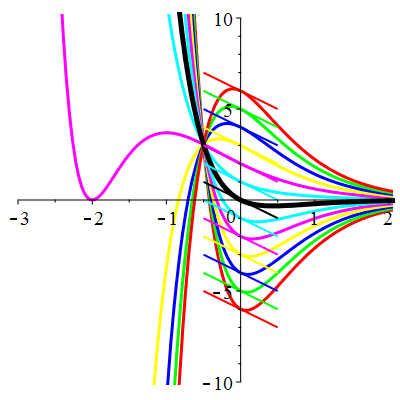
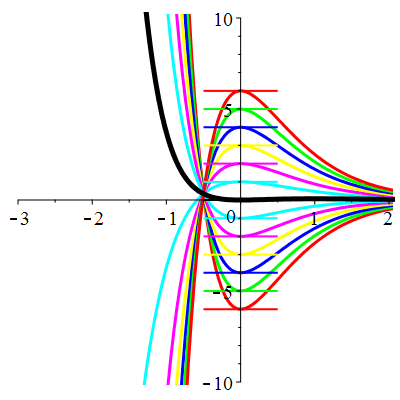
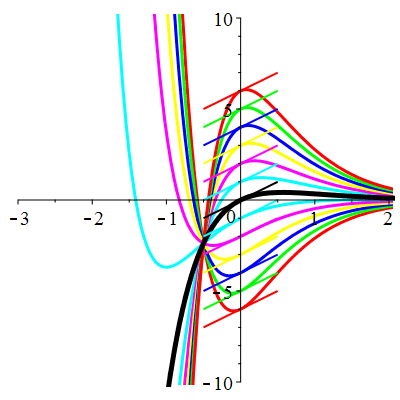
\(\vphantom{()_p^b}\) \(a=4\qquad b=4\qquad \varphi(t)=\,\mathrm{e}^{-2t}\)
| Solution : |
\(u(t)\!=\!\big(\frac12t^2\!+\!\lambda\,t\!+\!\mu\big)\mathrm{e}^{-2t}\) |
Courbes concourantes en 0
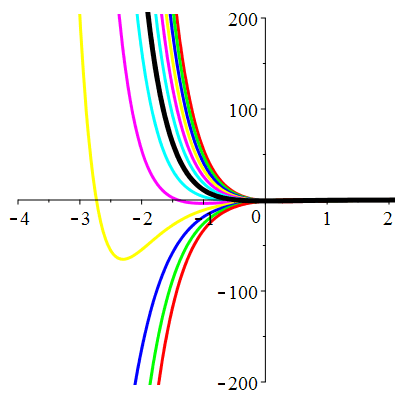
|
|
| \(u(0)=-1\) | Zoom |
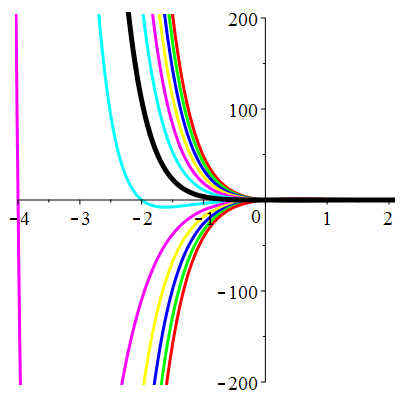
|
|
| \(u(0)=0\) | Zoom |
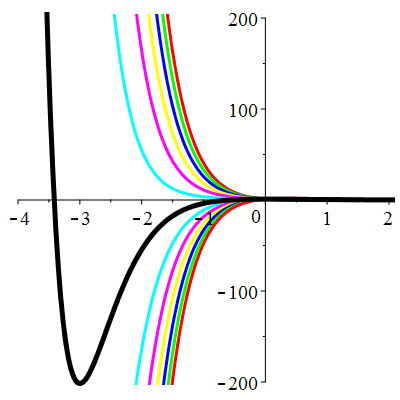
|
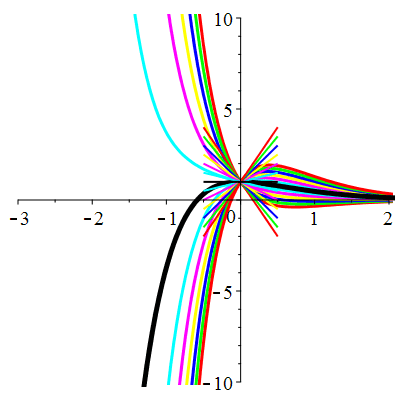
|
| \(u(0)=1\) | Zoom |
Courbes de pente constante en 0
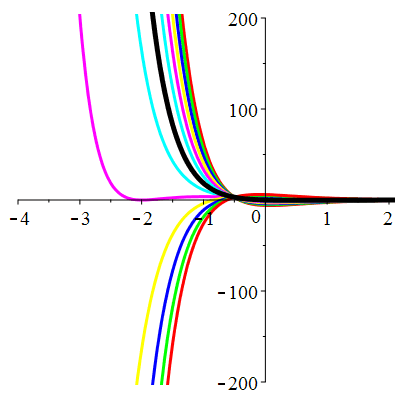
|
|
| \(\dot{u}(0)=-2\) | Zoom |
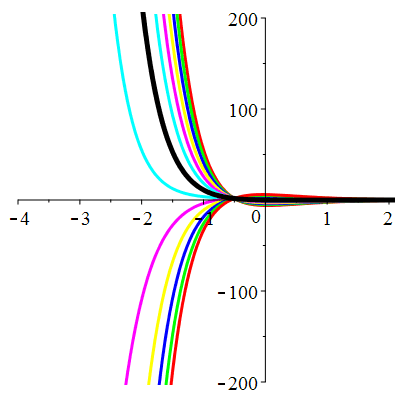
|
|
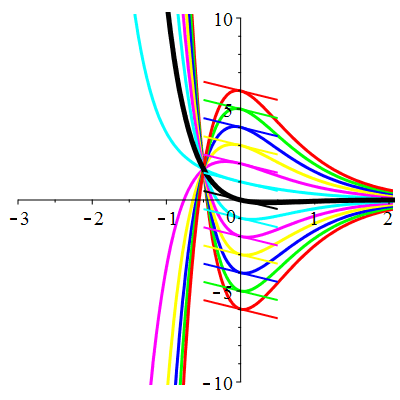
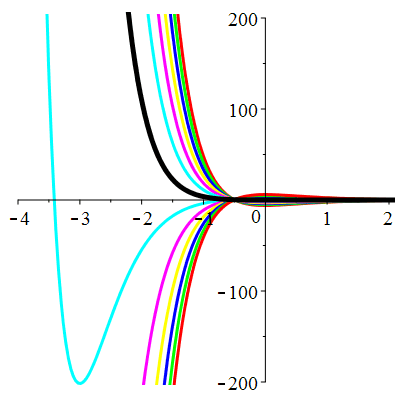
| \(\dot{u}(0)=-1\) | Zoom |
|
|
| \(\dot{u}(0)=0\) | Zoom |
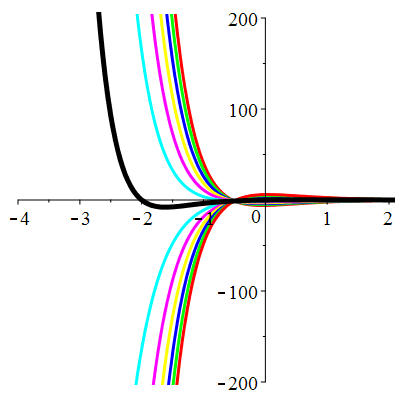
|

|
| \(\dot{u}(0)=1\) | Zoom |
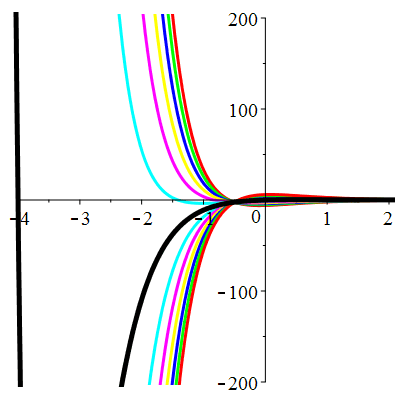
|
|
| \(\dot{u}(0)=2\) | Zoom |
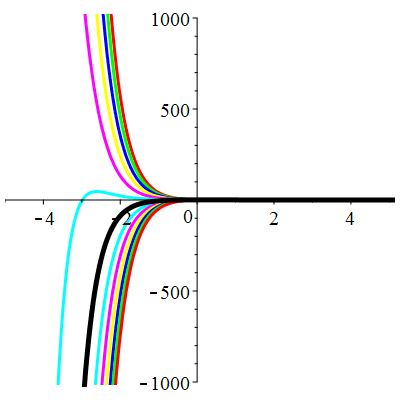
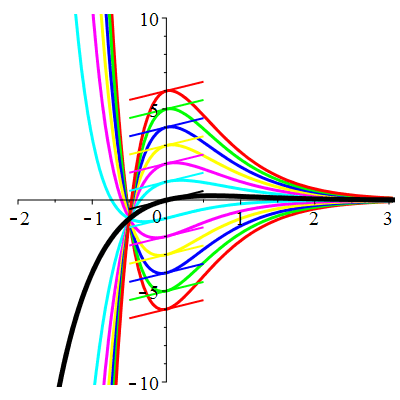
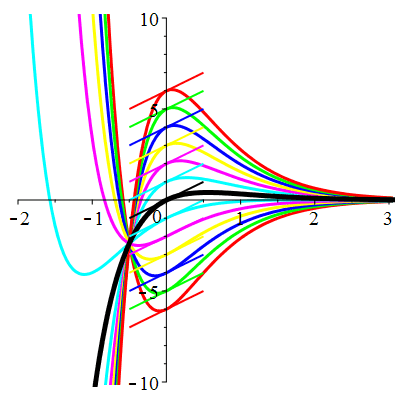
\(\vphantom{()_p^b}\) \(a=4\qquad b=4\qquad \varphi(t)=\,\mathrm{e}^{-2t}\cos t\)
| Solution : |
\(u(t)\!=\!(\lambda\,t\!+\!\mu)\mathrm{e}^{-2t}\!-\!\mathrm{e}^{-2t}\cos t\) |
Courbes concourantes en 0
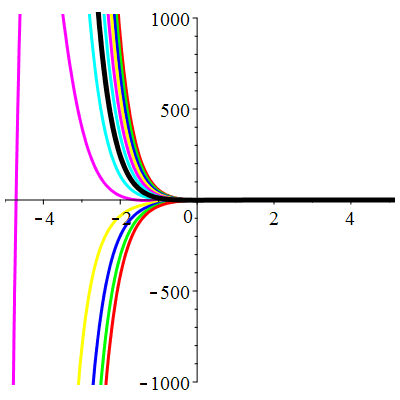
|
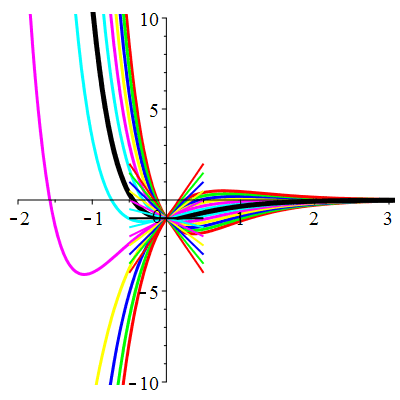
|
| \(u(0)=-1\) | Zoom |
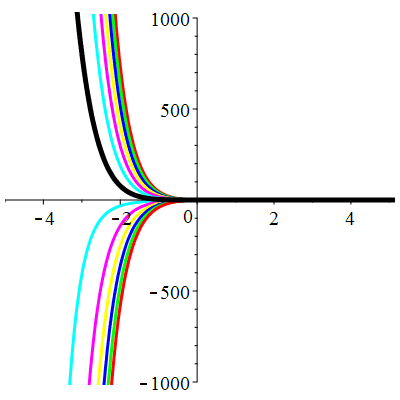
|
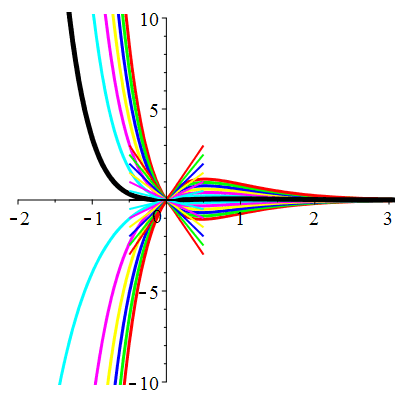
|
| \(u(0)=0\) | Zoom |
|
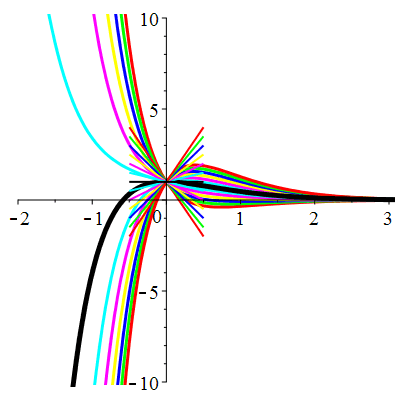
|
| \(u(0)=1\) | Zoom |
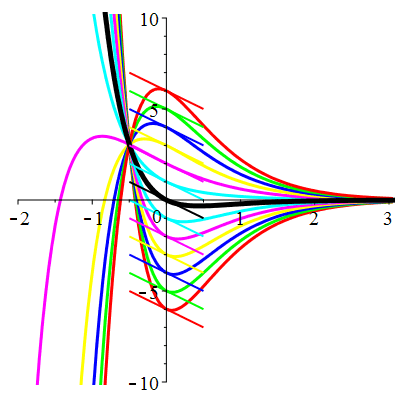
Courbes de pente constante en 0
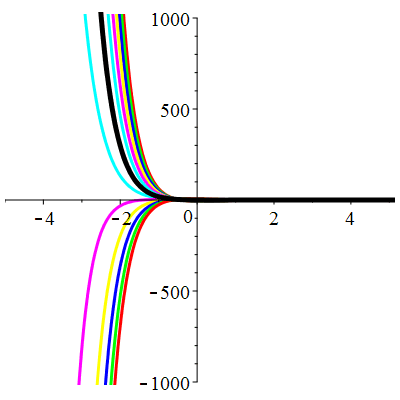
|
|
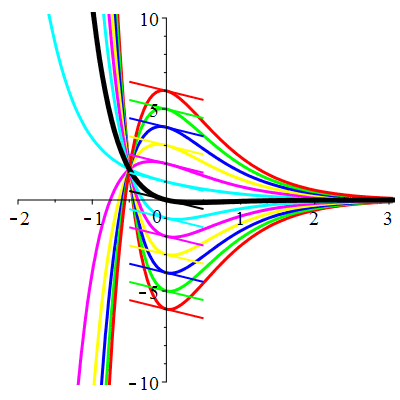
| \(\dot{u}(0)=-2\) | Zoom |
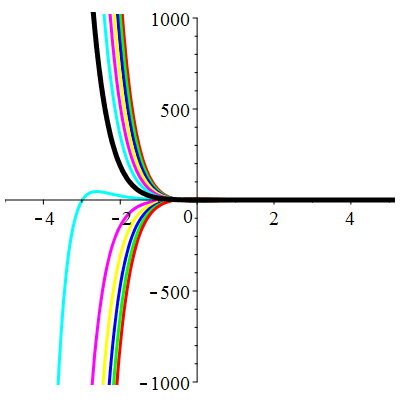
|
|
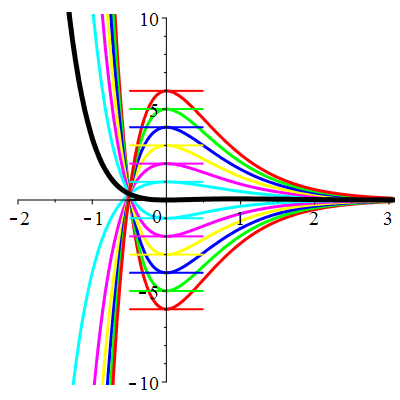
| \(\dot{u}(0)=-1\) | Zoom |
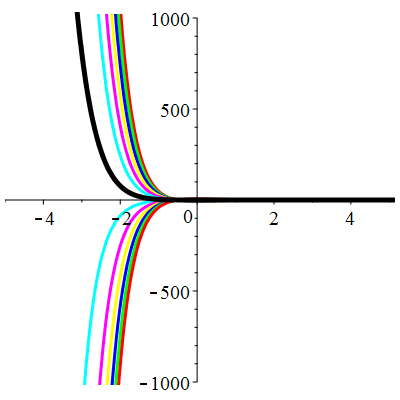
|
|
| \(\dot{u}(0)=0\) | Zoom |
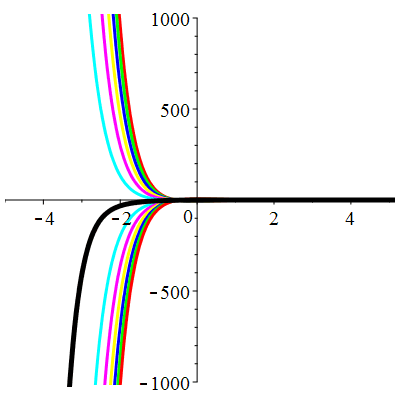
|
|
| \(\dot{u}(0)=1\) | Zoom |
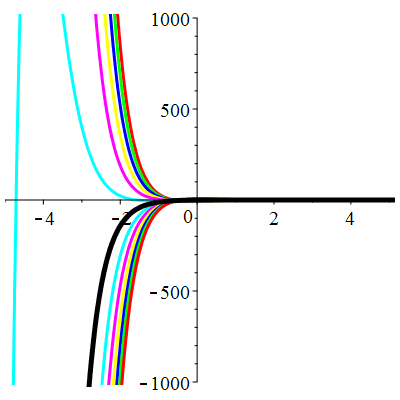
|
|
| \(\dot{u}(0)=2\) | Zoom |
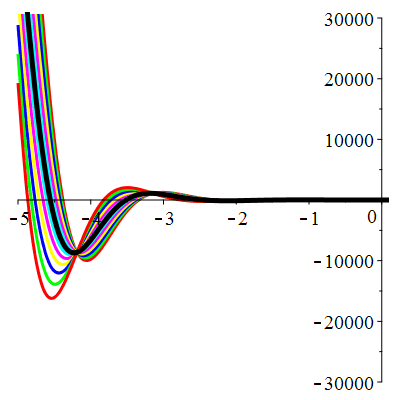
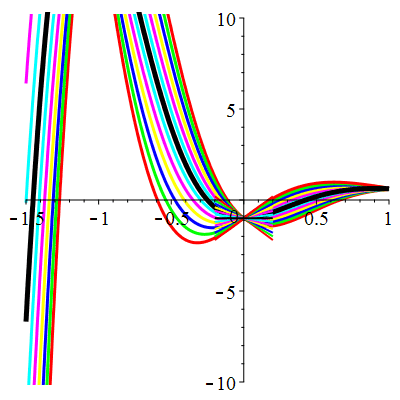
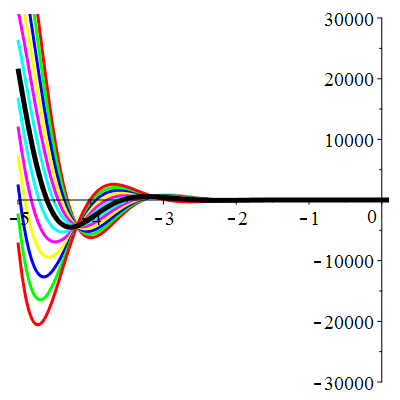
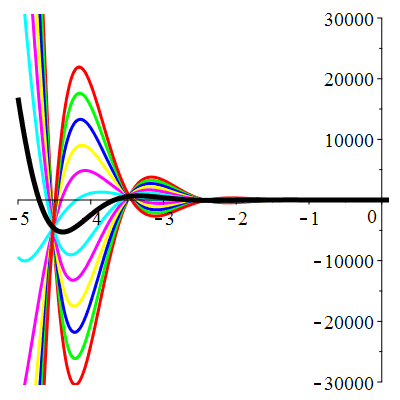
\(\vphantom{()_p^b}\) \(a=4\qquad b=13\qquad \varphi(t)=10\,\mathrm{e}^{-t}\)
| Solution : |
\(u(t)\!=\!\big[\lambda\cos(3t)\!+\!\mu\sin(3t)\big]\mathrm{e}^{-2t}\!+\hspace{-0.1em}\mathrm{e}^{-t}\) |
Courbes concourantes en 0
|
|
| \(u(0)=-1\) | Zoom |
|
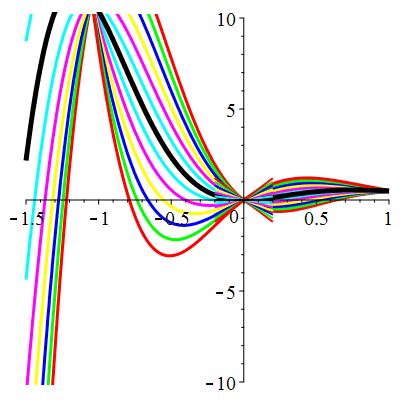
|
| \(u(0)=0\) | Zoom |
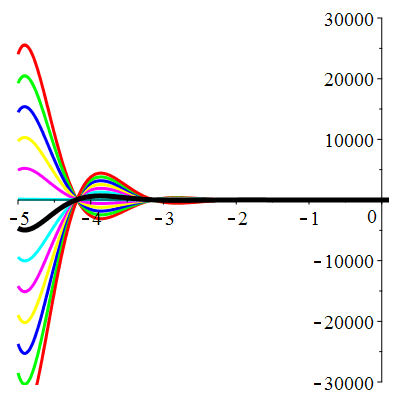
|
|
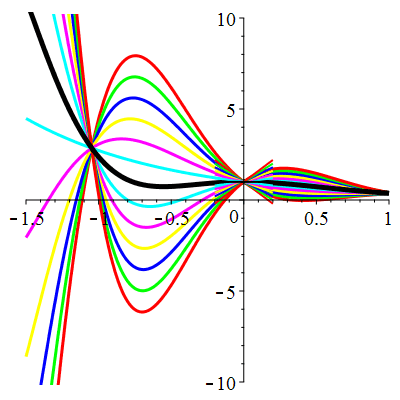
| \(u(0)=1\) | Zoom |
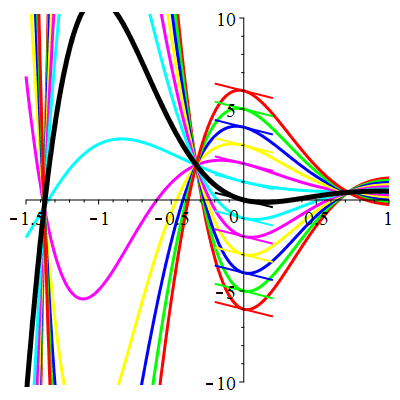
Courbes de pente constante en 0
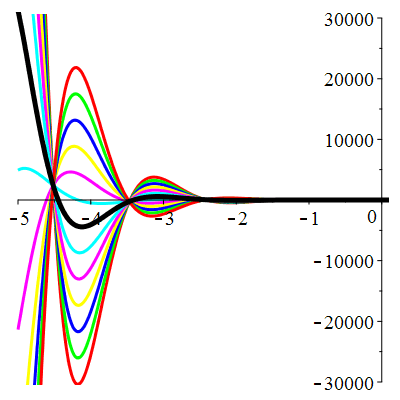
|
|
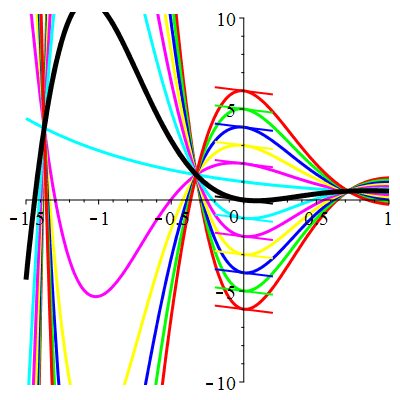
| \(\dot{u}(0)=-2\) | Zoom |
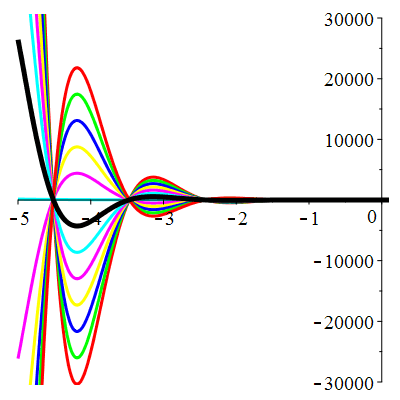
|
|
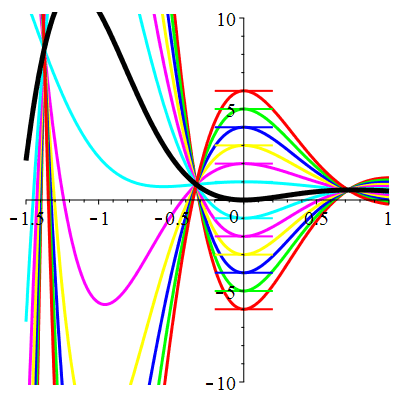
| \(\dot{u}(0)=-1\) | Zoom |
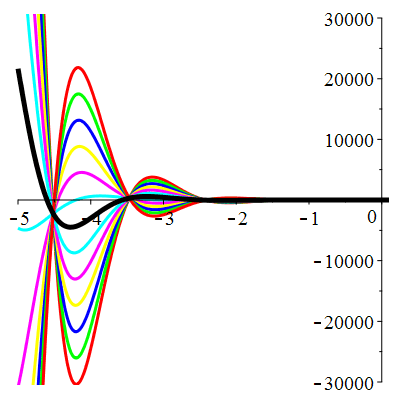
|
|
| \(\dot{u}(0)=0\) | Zoom |
|
|
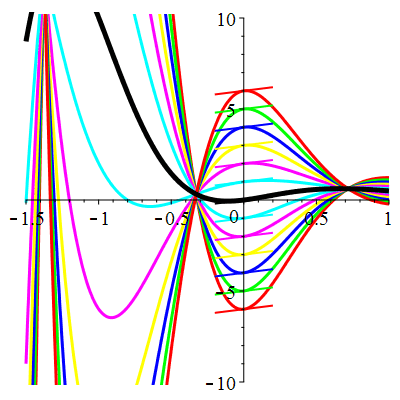
| \(\dot{u}(0)=1\) | Zoom |
|
|
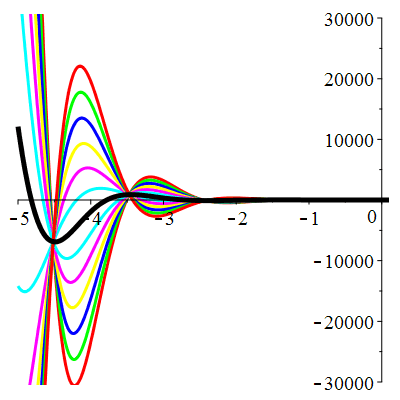
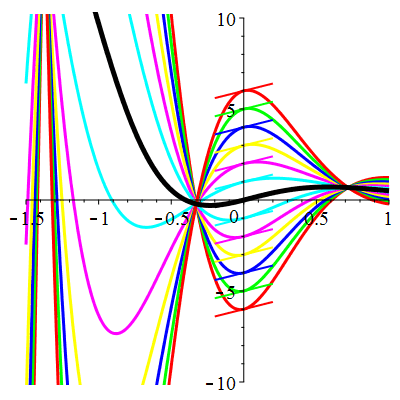
| \(\dot{u}(0)=2\) | Zoom |
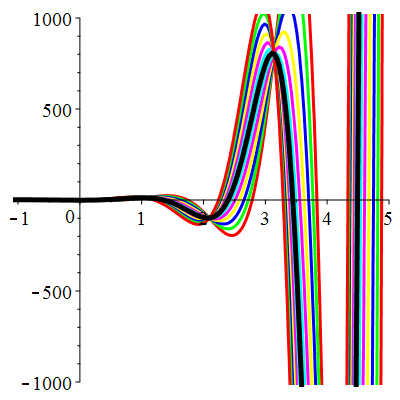
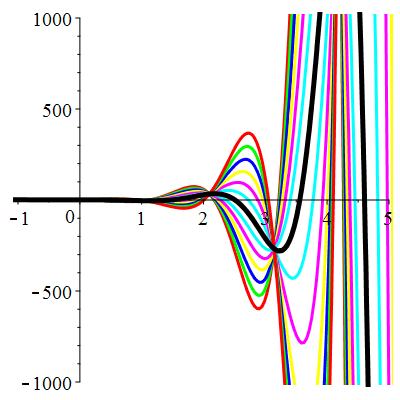
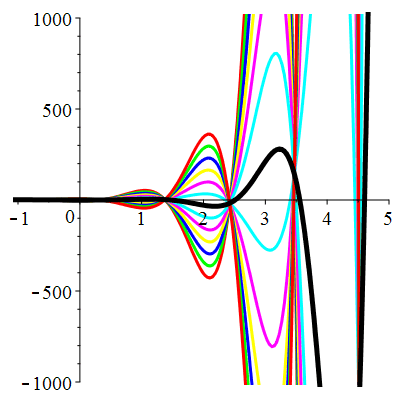
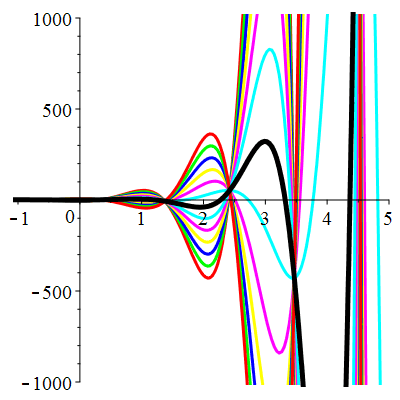
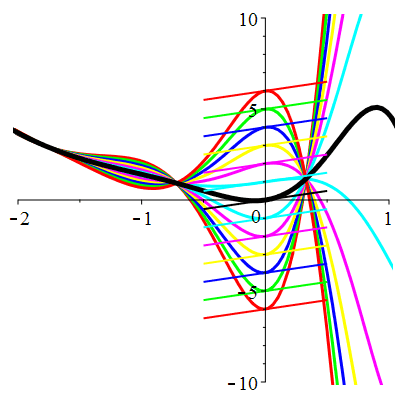
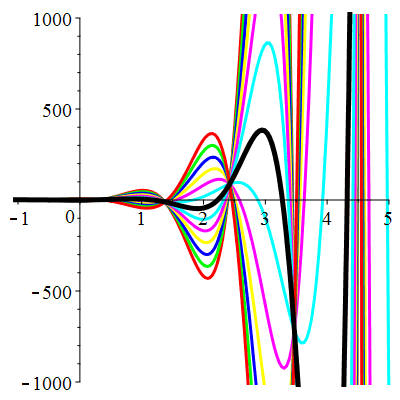
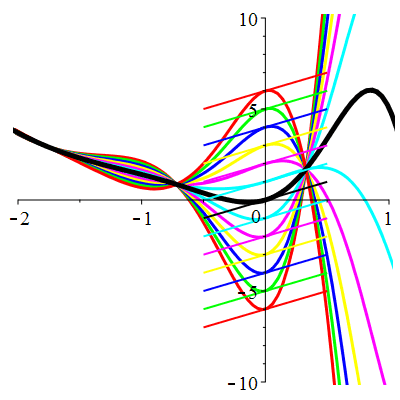
\(\vphantom{()_p^b}\) \(a=-4\qquad b=13\qquad \varphi(t)=9\,\mathrm{e}^{-t}\)
| Solution : |
\(u(t)\!=\!\big[\lambda\cos(3t)\!+\!\mu\sin(3t)\big]\mathrm{e}^{2t}\!+\!\frac12\mathrm{e}^{-t}\) |
Courbes concourantes en 0
|
|
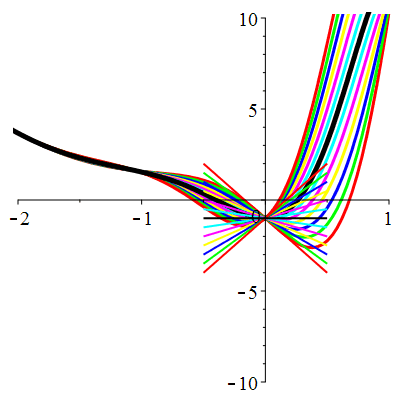
| \(u(0)=-1\) | Zoom |
|
|
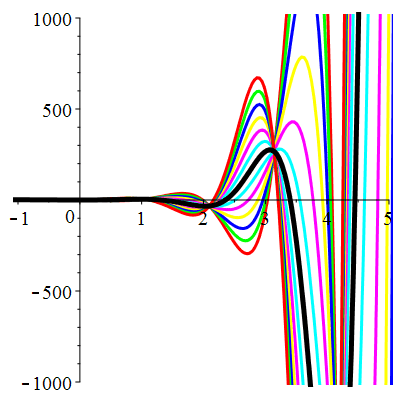
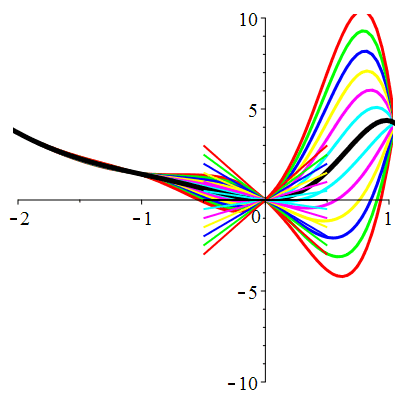
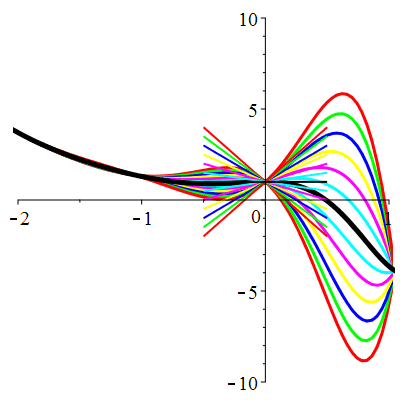
| \(u(0)=0\) | Zoom |
|
|
| \(u(0)=1\) | Zoom |
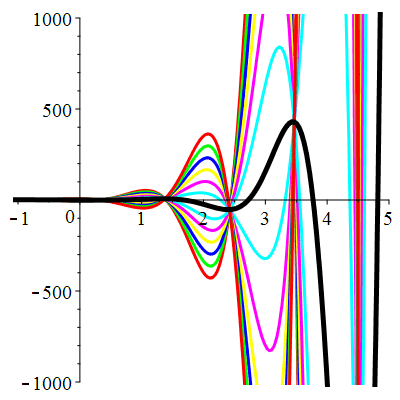
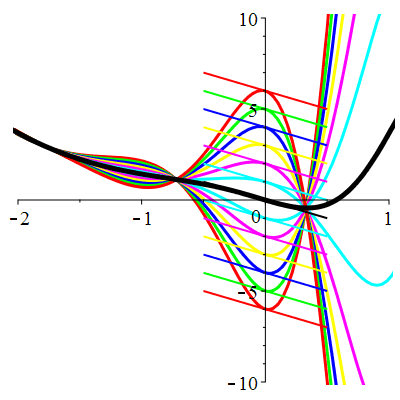
Courbes de pente constante en 0
|
|
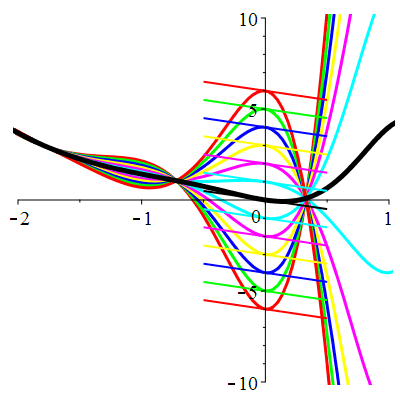
| \(\dot{u}(0)=-2\) | Zoom |
|
|
| \(\dot{u}(0)=-1\) | Zoom |
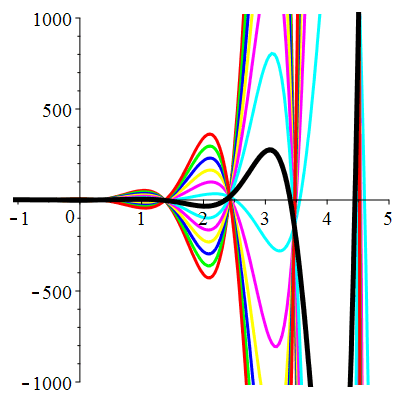
|
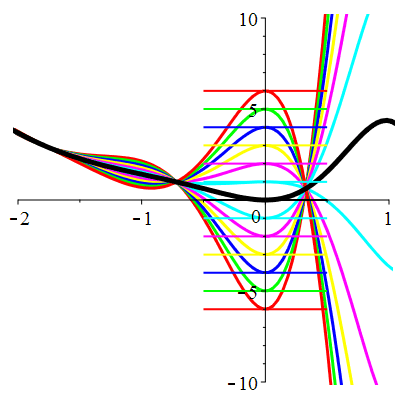
|
| \(\dot{u}(0)=0\) | Zoom |
|
|
| \(\dot{u}(0)=1\) | Zoom |
|
|
| \(\dot{u}(0)=2\) | Zoom |
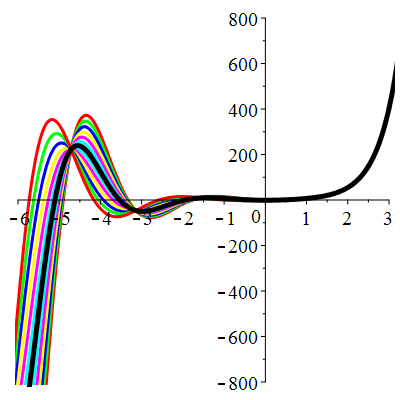
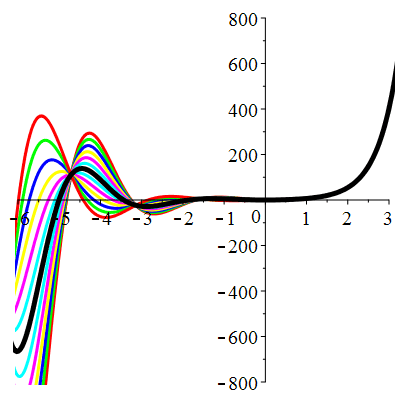
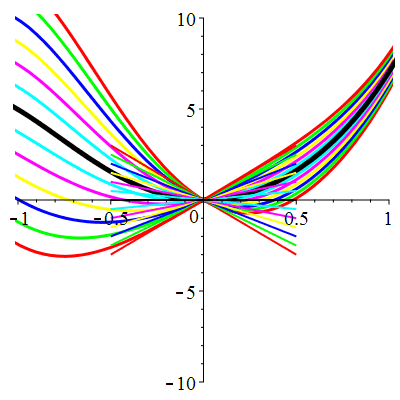
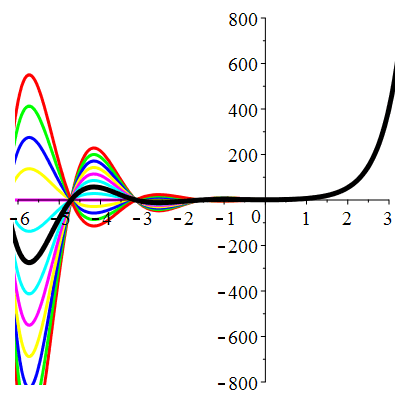
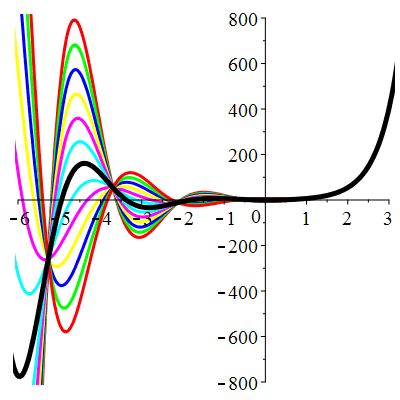
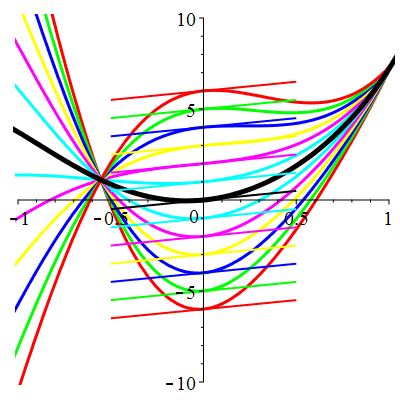
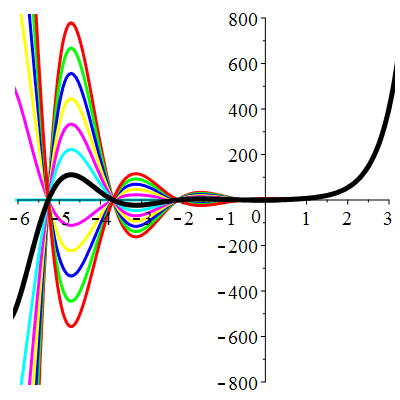
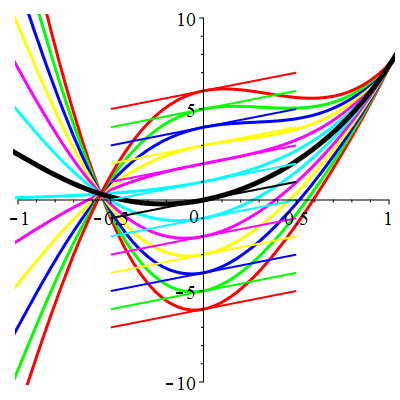
\(\vphantom{()_p^b}\) \(a=2\qquad b=5\qquad \varphi(t)=13\,\mathrm{e}^{2t}\)
| Solution : |
\(u(t)\!=\!\big[\lambda\cos(2t)\!+\!\mu\sin(2t)\big]\mathrm{e}^{-t}\!+\!\mathrm{e}^{2t}\) |
Courbes concourantes en 0
|
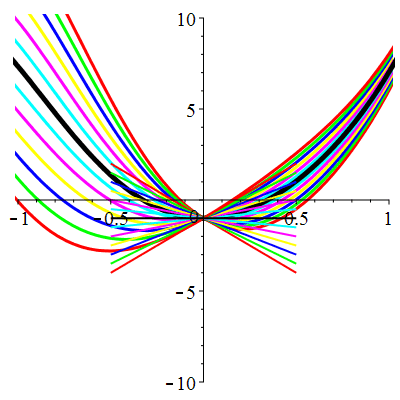
|
| \(u(0)=-1\) | Zoom |
|
|
| \(u(0)=0\) | Zoom |
|
|
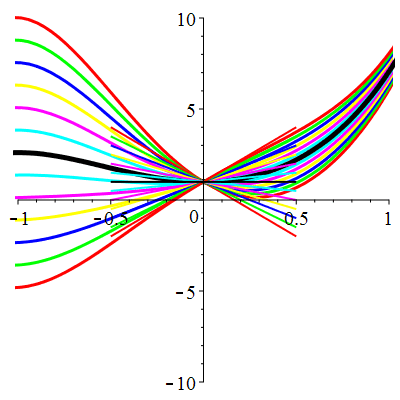
| \(u(0)=1\) | Zoom |
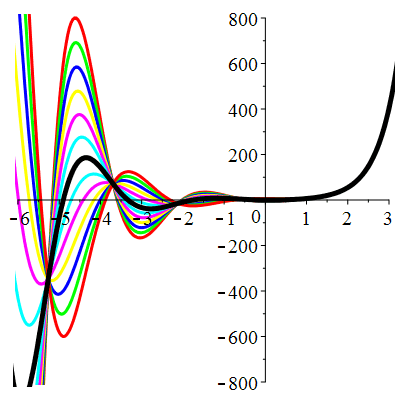
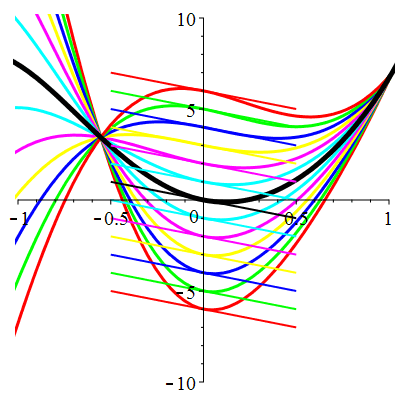
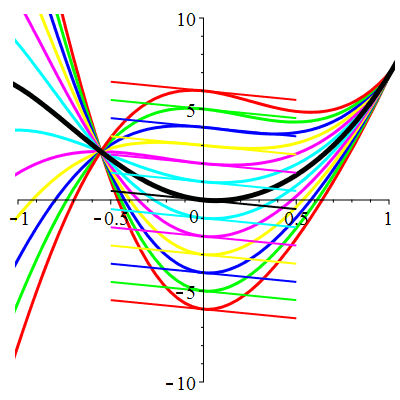
Courbes de pente constante en 0
|
|
| \(\dot{u}(0)=-2\) | Zoom |
|
|
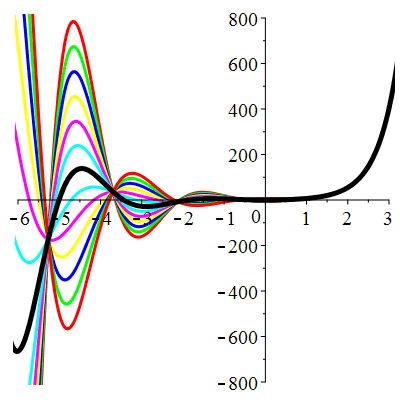
| \(\dot{u}(0)=-1\) | Zoom |
|

|
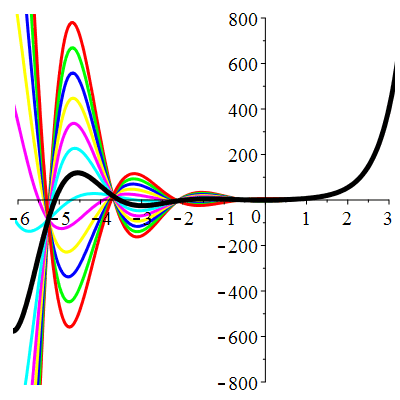
| \(\dot{u}(0)=0\) | Zoom |
|
|
| \(\dot{u}(0)=1\) | Zoom |
|
|
| \(\dot{u}(0)=2\) | Zoom |
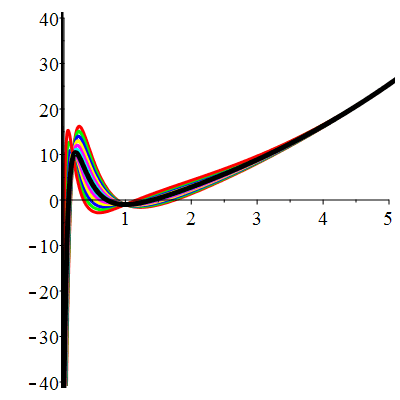
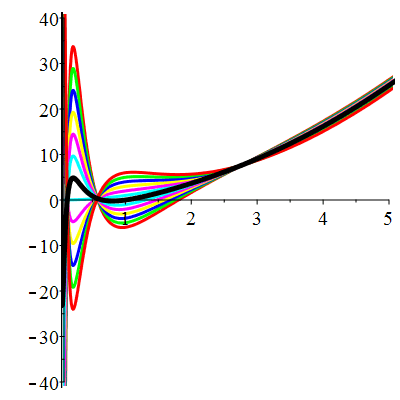
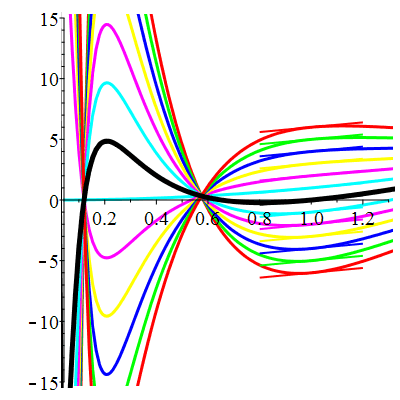
\(\vphantom{\dfrac{b^a}{q}}\) \(a(t)=\dfrac{3}{t}\qquad b(t)=\dfrac{5}{t^2}\qquad \varphi(t)=13\)
| Solution : |
|
\(u(t) \!=\!\begin{cases}
\raise -1ex {\lambda_1\dfrac{\cos(2\ln|t|)}{t}\!+\!\mu_1\dfrac{\sin(2\ln|t|)}{t}\!+t^2}\\[-0.5ex]
\scriptstyle\text{si } t\in\mathopen]-\infty,0[\\[0.5ex]
\lambda_2\dfrac{\cos(2\ln|t|)}{t}\!+\!\mu_2\dfrac{\sin(2\ln|t|)}{t}\!+t^2\\[-0.5ex]
\scriptstyle\text{si } t\in\mathopen]0,+\infty[
\end{cases}\)
|
|
| Pour \(\lambda_1\!=\!\lambda_2\!=\!\mu_1\!=\!\mu_2\!=\!0:\) |
| \(u(t)\!=\!t^2, \;{\scriptstyle t\in\mathbb{R}}\) |
| dérivable en 0 |
|
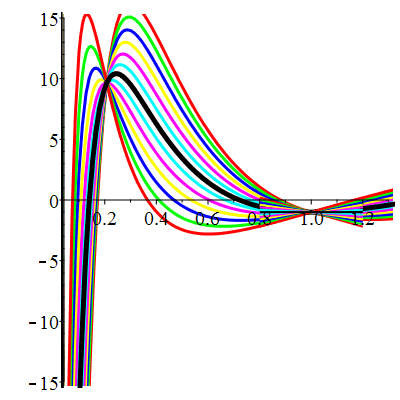
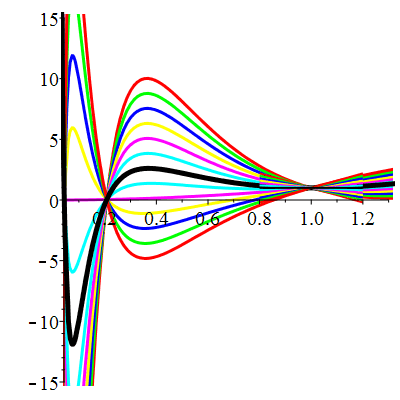
Courbes concourantes en 1
|
|
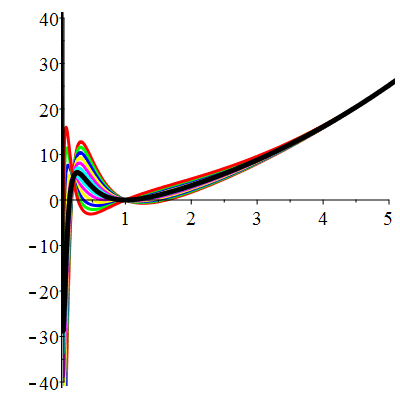
| \(u(1)=-1\) | Zoom |
|
|
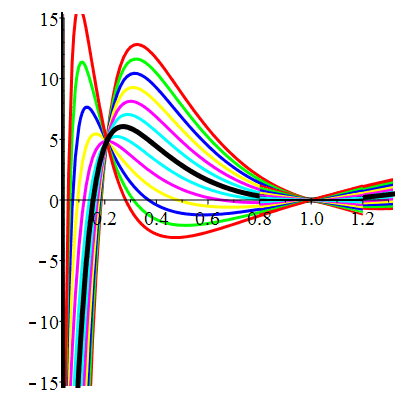
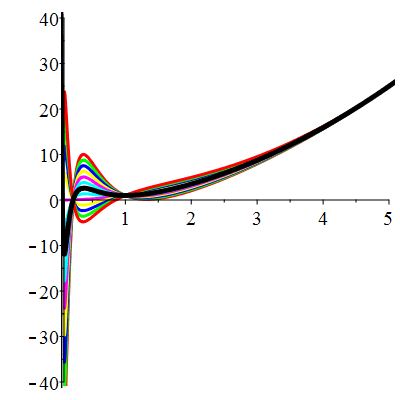
| \(u(1)=0\) | Zoom |
|
|
| \(u(1)=1\) | Zoom |
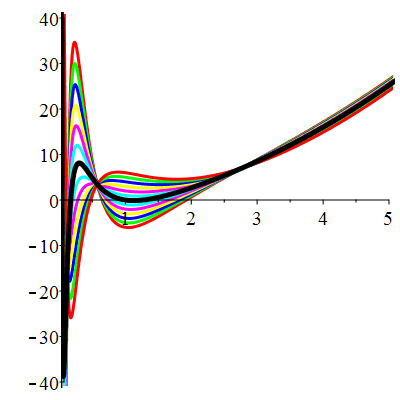
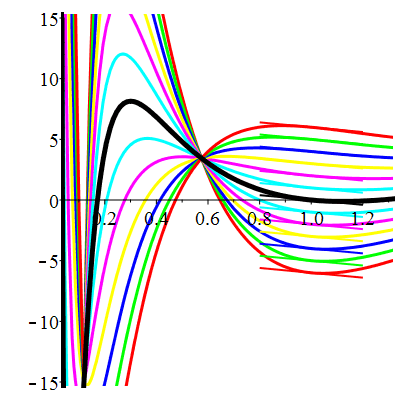
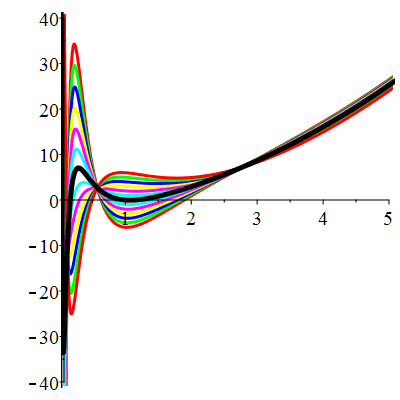
Courbes de pente constante en 1
|
|
| \(\dot{u}(1)=-2\) | Zoom |
|
|
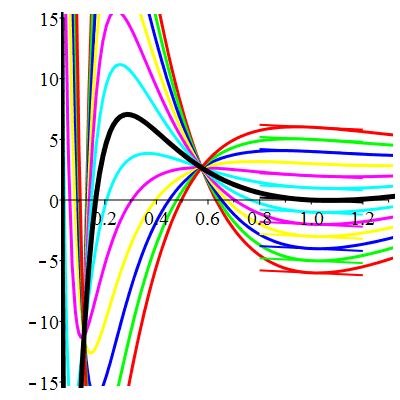
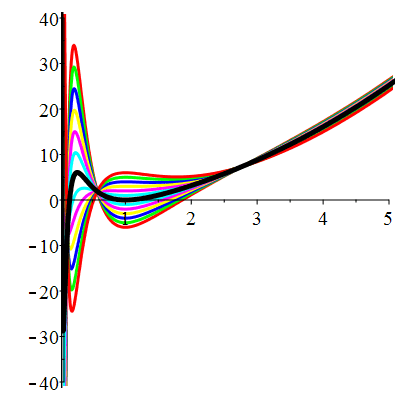
| \(\dot{u}(1)=-1\) | Zoom |
|
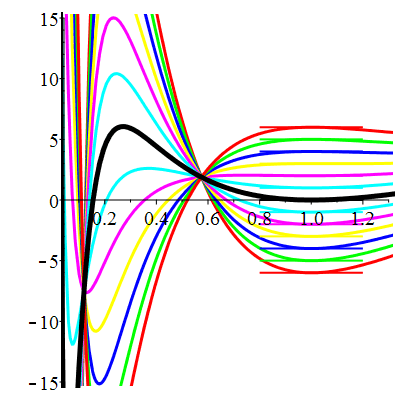
|
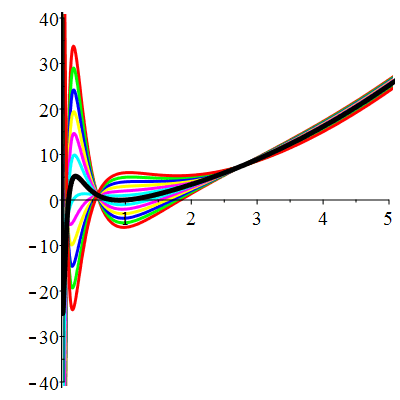
| \(\dot{u}(1)=0\) | Zoom |
|
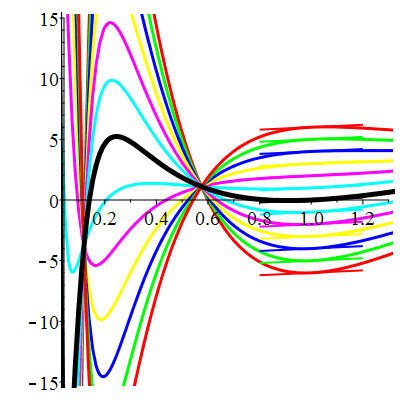
|
| \(\dot{u}(1)=1\) | Zoom |
|
|
| \(\dot{u}(1)=2\) | Zoom |