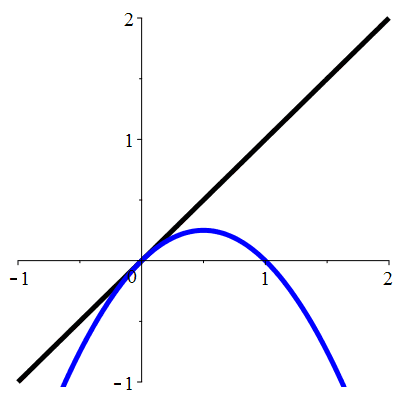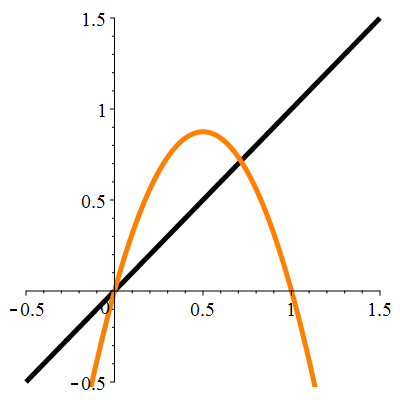| V. Autre cas : la suite logistique |
Exemple 6a
| \(\color{blue}f(x)\!=\!x(1-x)\) |
\(u_0\!=\!0.8\) |
| Point fixe :
|
\(\color{blue}\ell\!=\!0\)
|
| Dérivée au point fixe :
| \(\color{blue}f'(\ell)\!=\!1\) |
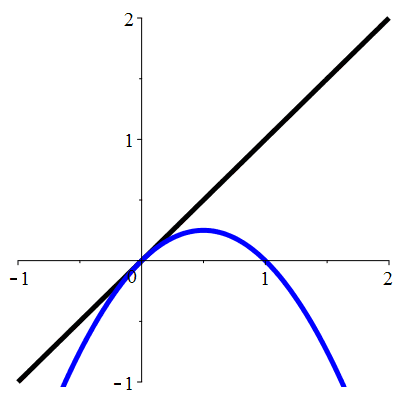
Aperçu global
animation 
stop 
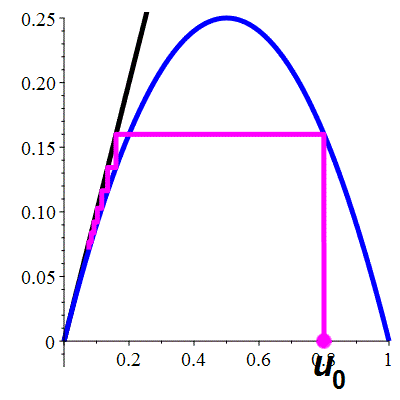
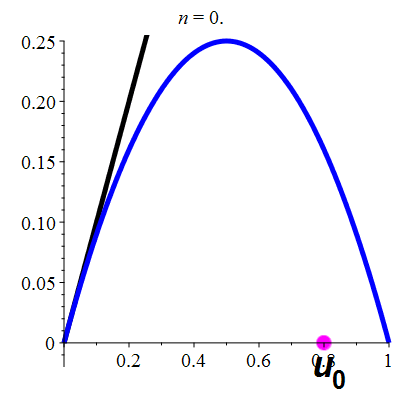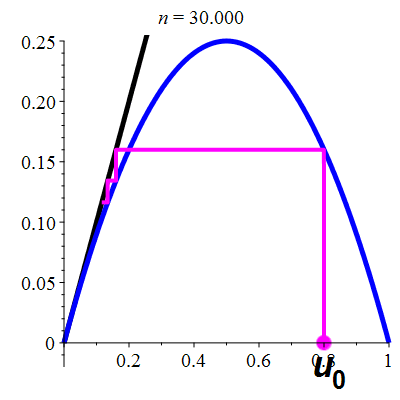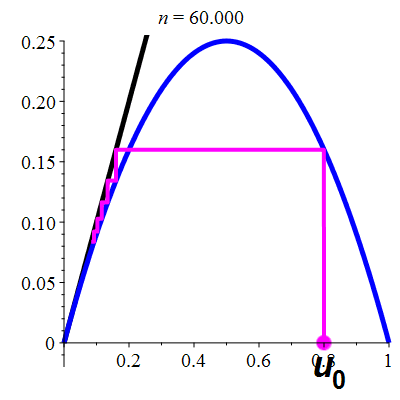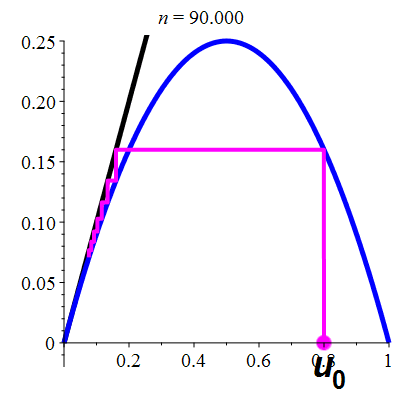
La suite \((u_n)_{n\in\mathbb{N}}\)
est décroissante
et converge vers 0
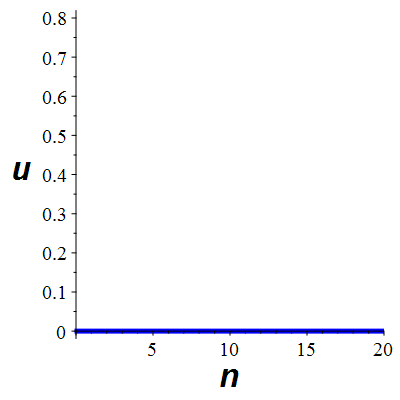
animation 
Exemple 6b
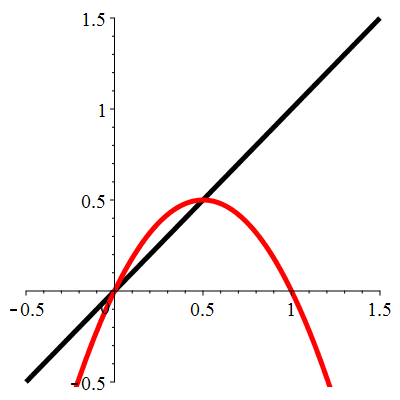
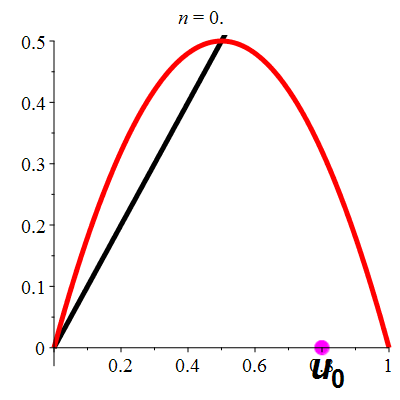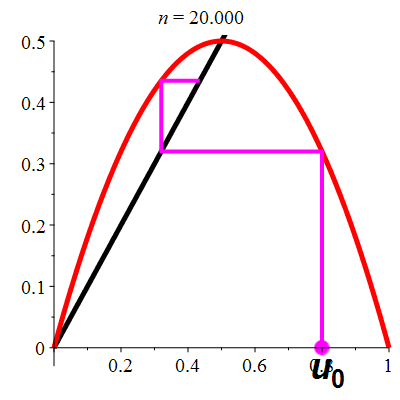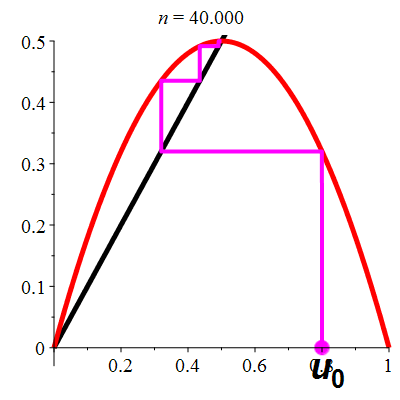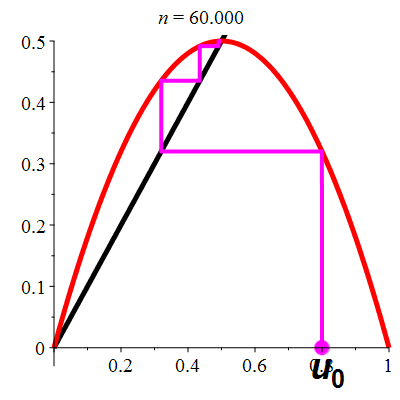
| \(\color{red}f(x)\!=\!2x(1-x)\) |
\(u_0\!=\!0.8\) |
| Points fixes : |
\(\color{red}\ell_1\!=\!0\) |
\(\color{red}\ell_2\!=\!\frac12\) |
| Dérivée aux points fixes : |
\(\color{red}f'(\ell_1)\!=\!2\) |
\(\color{red}f'(\ell_2)\!=\!0\) |
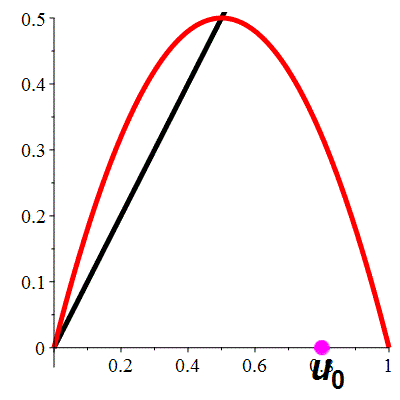
Aperçu global
animation 
stop 
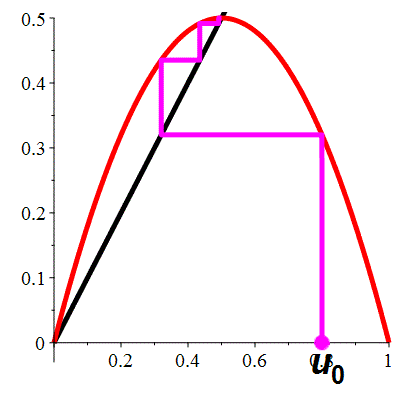
La suite \((u_n)_{n\in\mathbb{N}}\) converge vers \(\frac12\)
animation 
Exemple 6c
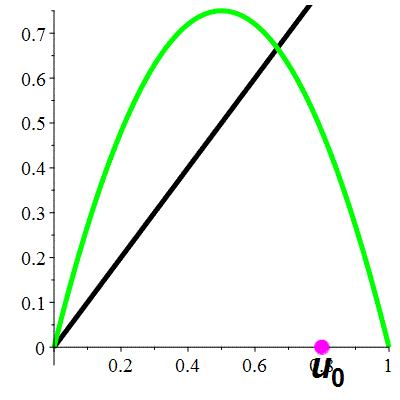
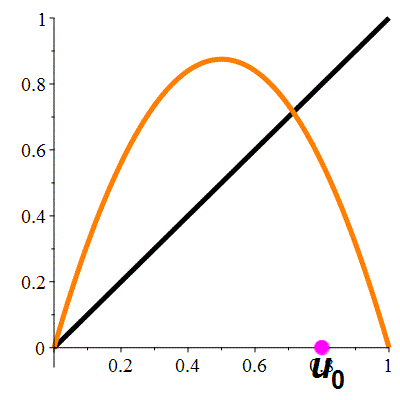
| \(\color{lime}f(x)\!=\!3x(1-x)\) |
\(u_0\!=\!0.8\) |
| Points fixes : |
\(\color{lime}\ell_1\!=\!0\) |
\(\color{lime}\ell_2\!=\!\frac23\) |
| Dérivée aux points fixes : |
\(\color{lime}f'(\ell_1)\!=\!3\) |
\(\color{lime}f'(\ell_2)\!=\!\!-1\) |
Aperçu global
animation 

stop 
La suite \((u_n)_{n\in\mathbb{N}}\) converge vers \(\frac23\)
animation 
Exemple 6d
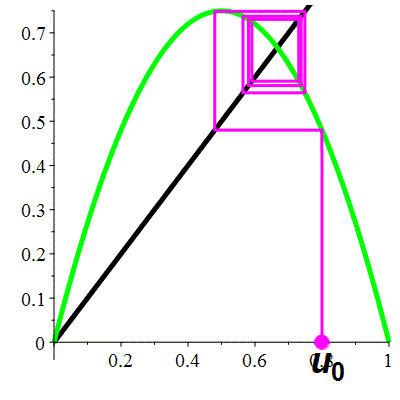
| \(\color{orange}f(x)\!=\!3.5x(1-x)\) |
\(u_0\!=\!0.8\) |
| Points fixes : |
\(\color{orange}\ell_1\!=\!0\) |
\(\color{orange}\ell_2\!=\!\frac57\) |
| Dérivée aux points fixes : |
\(\color{orange}f'(\ell_1)\!=\!3.5\) |
\(\color{orange}f'(\ell_2)\!=\!\!-1.5\) |
Aperçu global
animation 
animation 
Exemple 6e
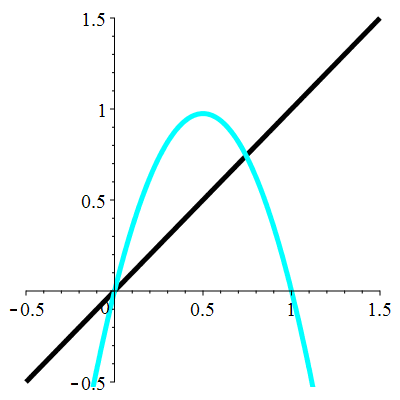
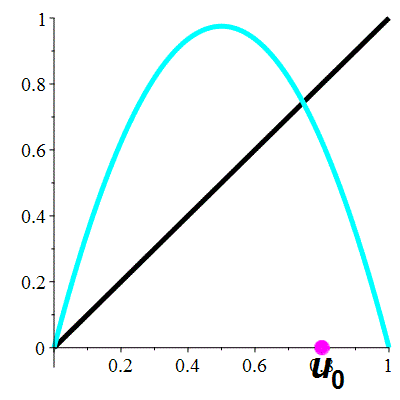
| \(\color{cyan}f(x)\!=\!3.9x(1-x)\) |
\(u_0\!=\!0.8\) |
| Points fixes : |
\(\color{cyan}\ell_1\!=\!0\) |
\(\color{cyan}\ell_2\!=\!\frac{29}{39}\approx0.743\) |
| Dérivée aux points fixes : |
\(\color{cyan}f'(\ell_1)\!=\!3.9\) |
\(\color{cyan}f'(\ell_2)\!=\!\!-1.9\) |
Aperçu global
animation 
animation 
Exemple 6f
| \(\color{gray}f(x)\!=\!4x(1-x)\) |
\(u_0\!=\!0.8\) |
| Points fixes : |
\(\color{gray}\ell_1\!=\!0\) |
\(\color{gray}\ell_2\!=\!\frac34\) |
| Dérivée aux points fixes : |
\(\color{gray}f'(\ell_1)\!=\!4\) |
\(\color{gray}f'(\ell_2)\!=\!\!-2\) |
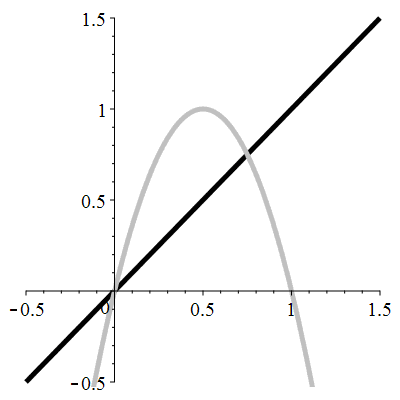
Aperçu global

animation 
animation 
Cas général : modèle logistique de Verhulst
|
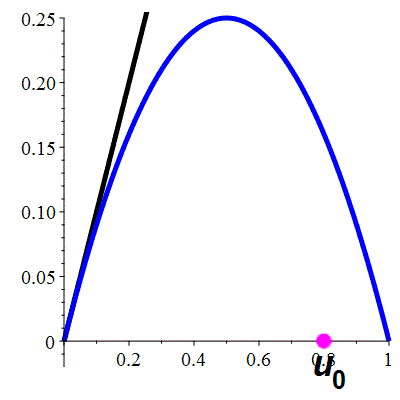
\(f(x)\!=\!ax(1-x)\quad\) \(x\!\in\![0,1]\)
|
|
\(u_0\!\in ]0,1[\;\) population initiale
|
| \(a\!\in\![0,4]\;\) paramètre du modèle |
| (taux de naissance) |
|
|
 |
| Pierre-François Verhulst |
| (1804–1849) |
| Mathématicien belge |
|
La condition \(a\!\in\![0,4]\) est nécessaire et suffisante pour assurer que
\(f([0,1])\!\subset\![0,1]\) et donc pour pouvoir définir la suite \((u_n)_{n\in\mathbb{N}}\).
- Si \(a\) est inférieur à 1, la population va s’éteindre : \(\ell=0.\)
- Si \(a\) est compris entre 1 et 3, la population croît et se stabilise à la valeur \(\ell=(a-1)/a.\)
- Au-delà de \(a\) = 3, l’évolution devient instable. C’est la première bifurcation.
- Si \(a\) est compris entre 3 et 3.449…, la population oscille entre deux valeurs
différentes correspondant aux deux branches du diagramme ci-dessous.
- Si \(a\) est compris entre 3.449… et 3.57…, la population oscille alternativement
entre 4 valeurs, puis 8 valeurs, 32 valeurs, etc. (voir diagramme ci-dessous).
- Au-delà de \(a\) = 3.57…, le chaos s’installe. De très légères variations des conditions initiales conduisent à des résultats radicalement différents.
L’évolution du système devient imprévisible sauf pour quelques valeurs de \(a\) exceptionnelles pour lesquelles on observe à nouveau des oscillations périodiques.
Un système dynamique non-linéaire est ainsi caractérisé par toute une famille de bifurcations conduisant à un chaos dynamique.
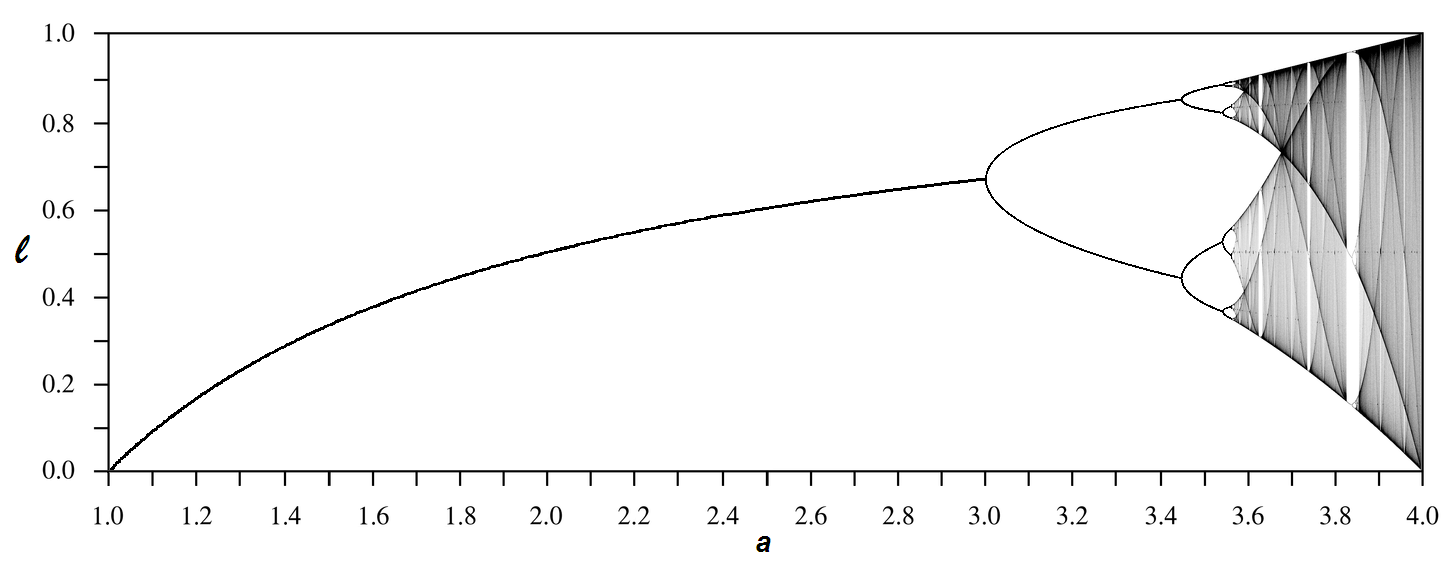
Diagramme de bifurcation
(Correspondance entre le paramètre du modèle et les points limites)
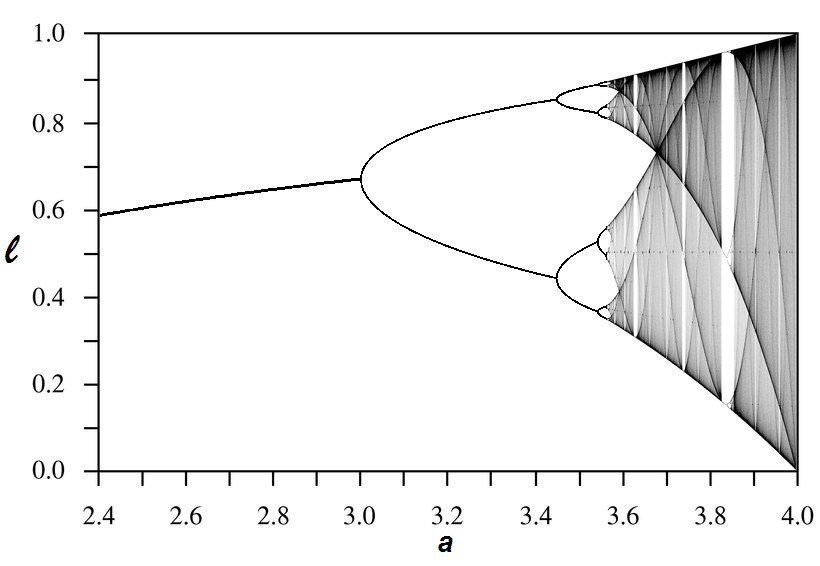
Zoom