On définit une expression f de la variable t :

et une fonction de la variable t :

On peut calculer l'image d'un réel :

On a affecté à t la valeur 1, mais pas 2.

On peut les dériver :

On peut les dériver plusieurs fois :

On calcule une primitive :

ou une intégrale :

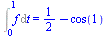
On peut aussi calculer des limites :

On peut calculer les dérivées partielles d'une fonction de 3 variables :

... puis son laplacien. Le laplacien est l'opérateur défini par

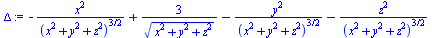
Simplifions le résultat :

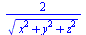
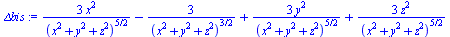
1/ est une fonction harmonique (laplacien nul)...