Maple peut tracer de jolies courbes et surfaces en tout genre...

On définit une expression f de la variable x que l'on fait tracer :

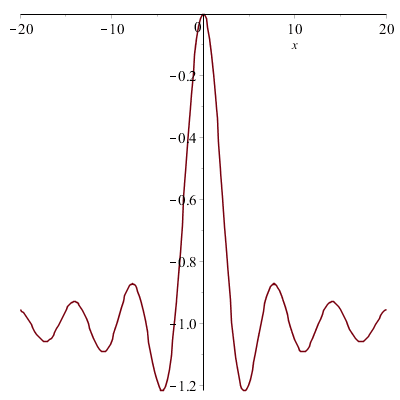
et une fonction g de la variable x que l'on fait également tracer :

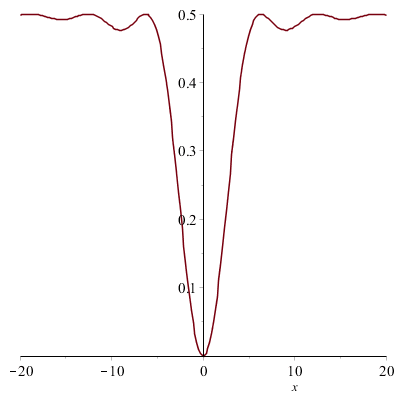
On peut représenter graphiquement les deux fonctions sur le même graphique :

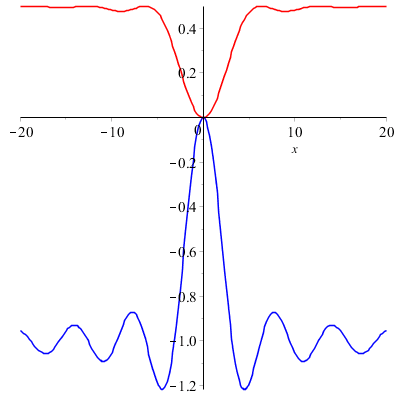
Ondes sinusoïdales

On peut afficher plusieurs courbes définies séparément sur un même dessin en chargeant la librairie "plots".
Superposons deux ondes sinusoïdales de même fréquence en quadrature  :

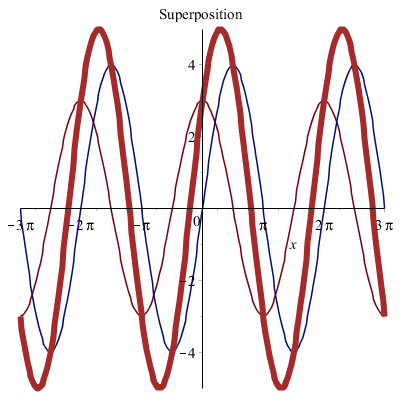
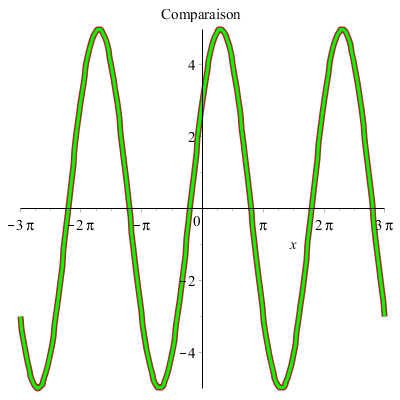
On a avec

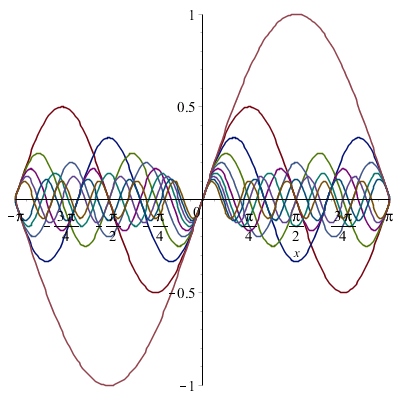
On peut tracer simultanément un plus grand nombre de courbes (avec une séquence) :

On peut faire des animations en chargeant la librairie "plots" :

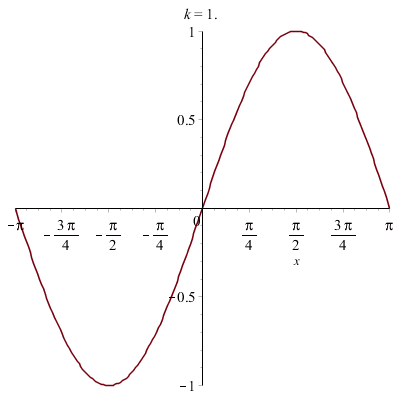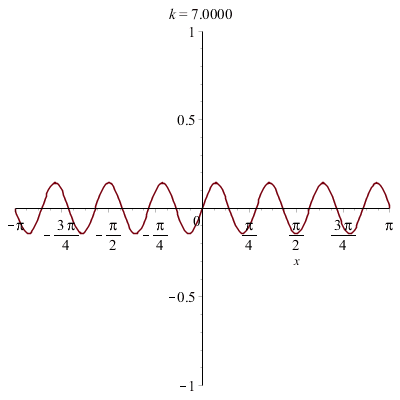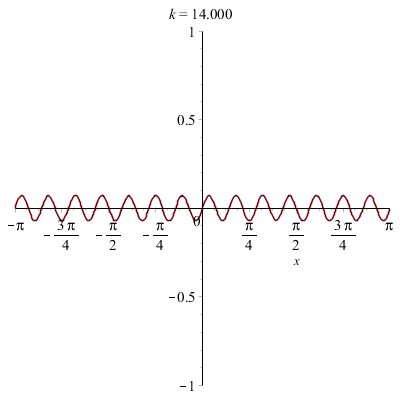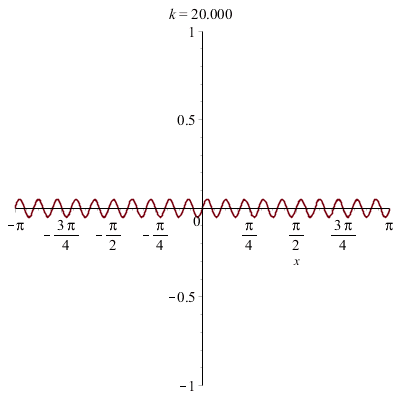
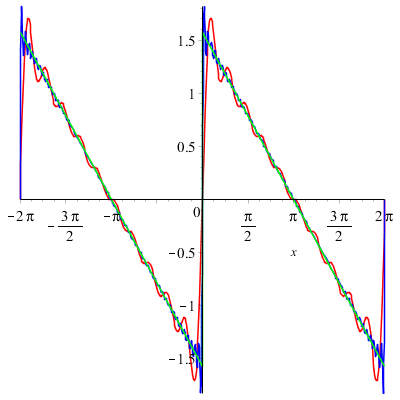
On a superposé plusieurs ondes sinusoïdales avec des fréquences multiples d'une fréquence initiale.

Fonctions puissances, polynomiales

Traçons la famille des fonctions puissances :

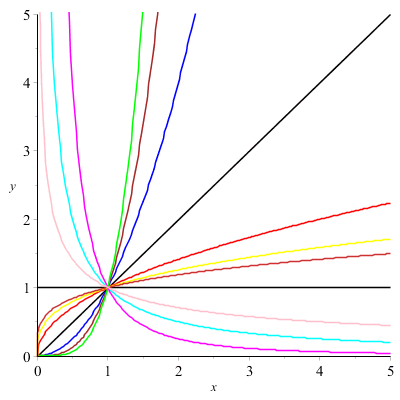
Quelques fonctions polynomiales :

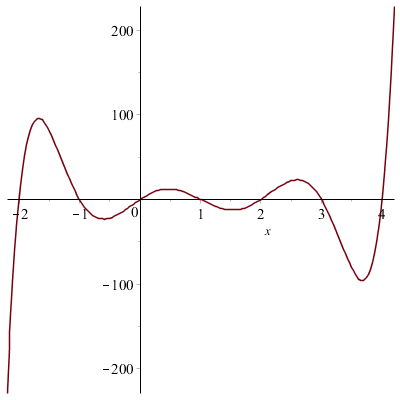
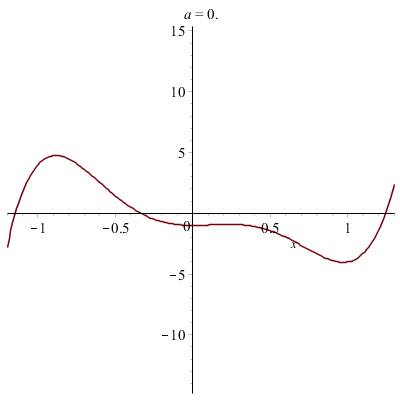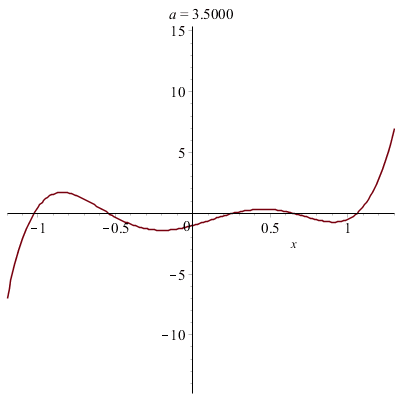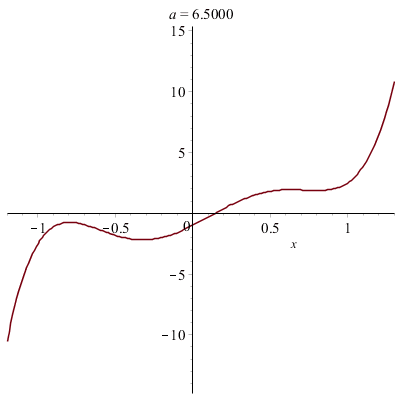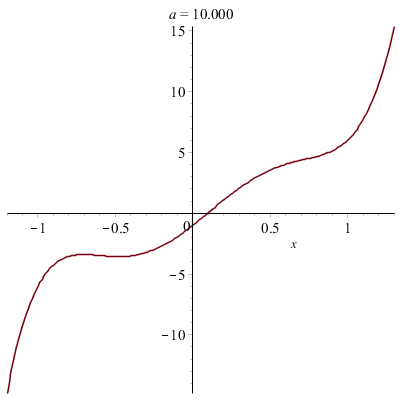
Du côté des fonctions hyperboliques...

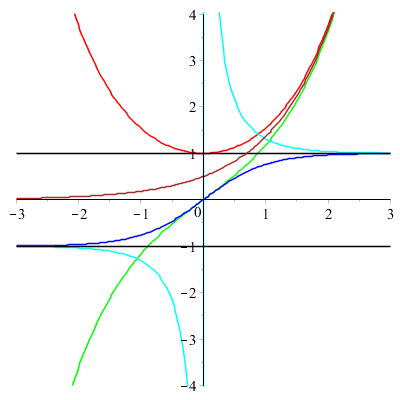
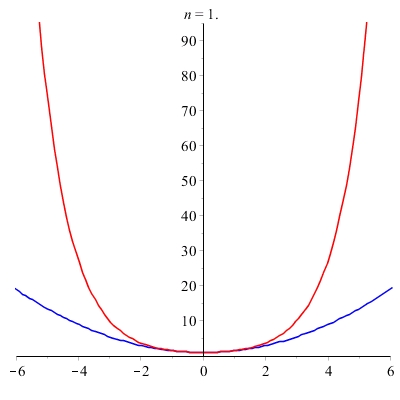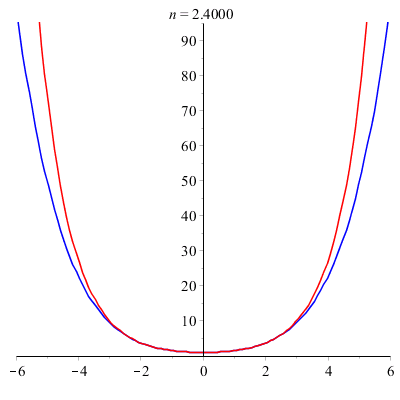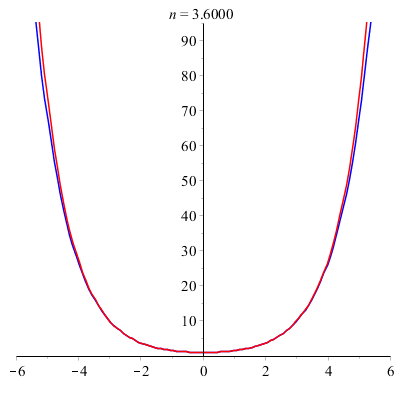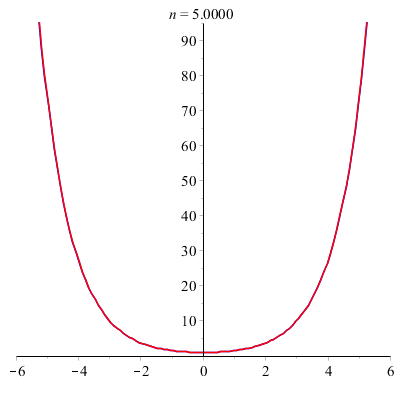
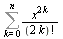est une approximation de ch(x).

Translations, homothéties

Déformations horizontales et verticales d'un graphe :

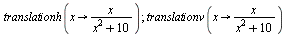
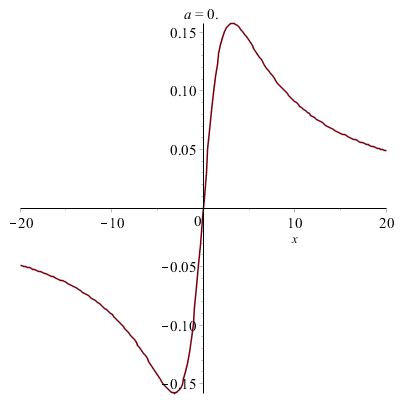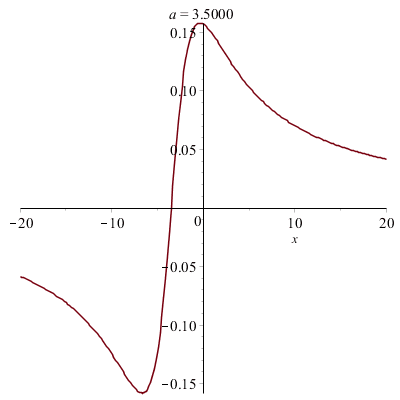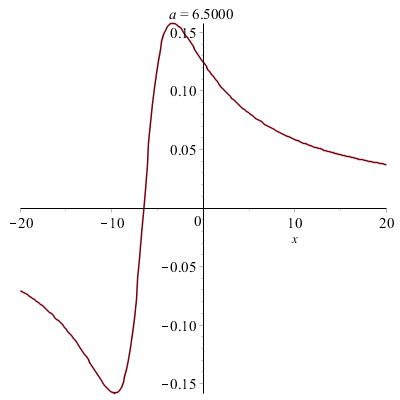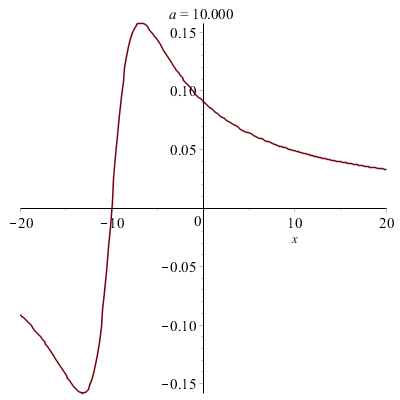
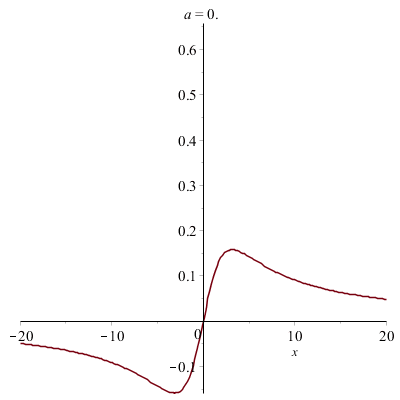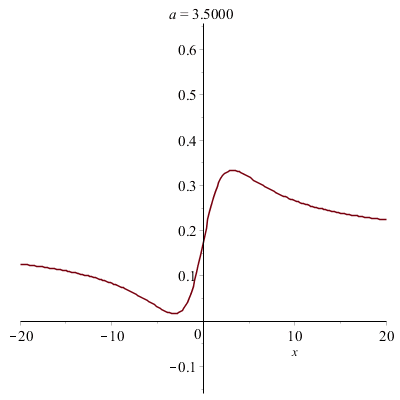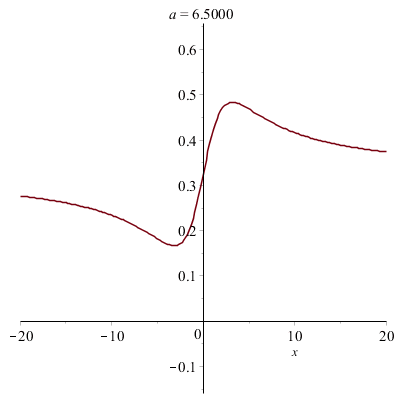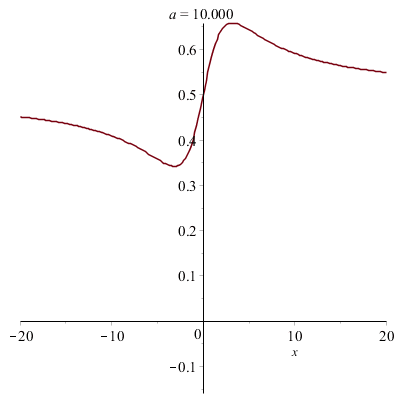
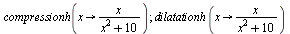
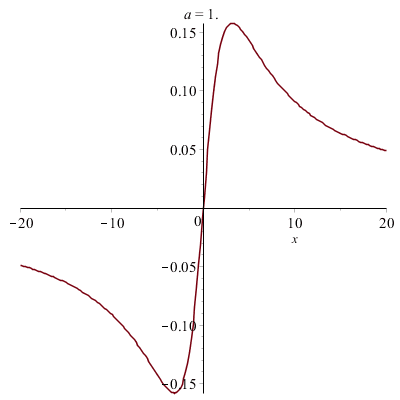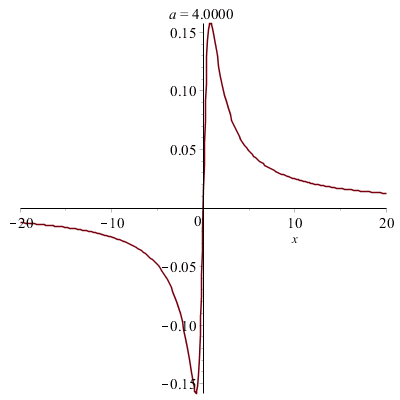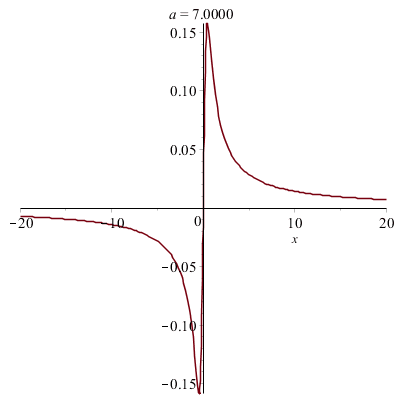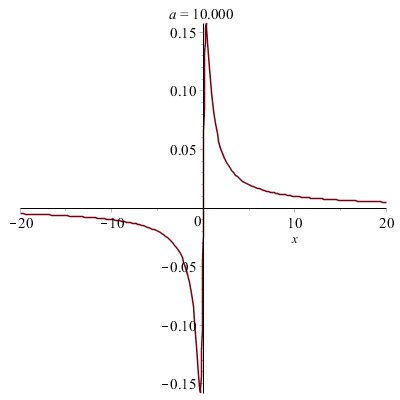
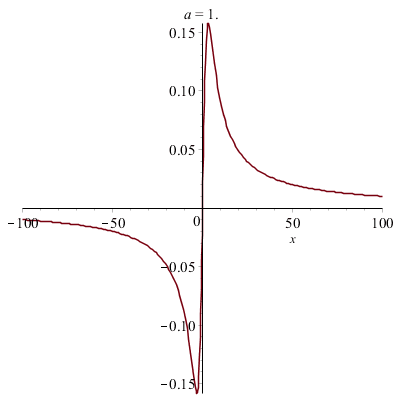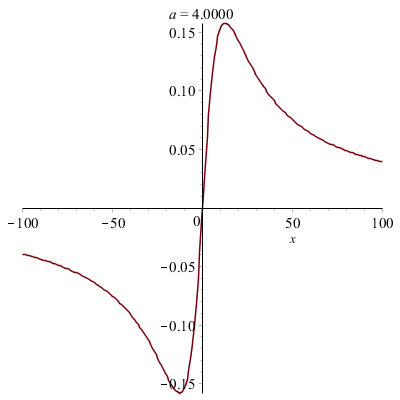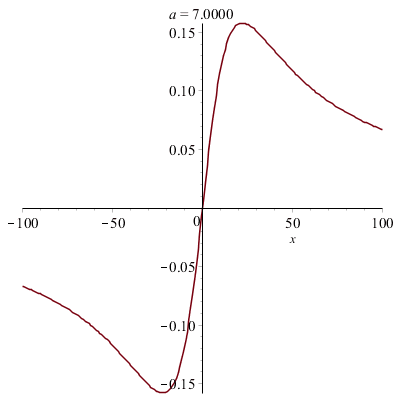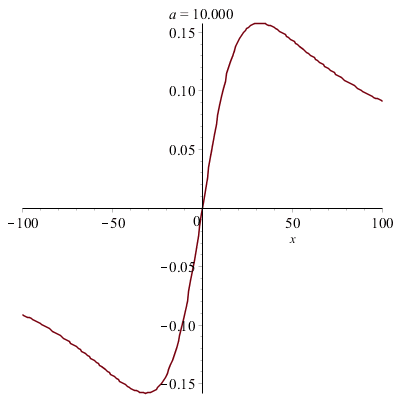
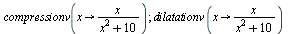
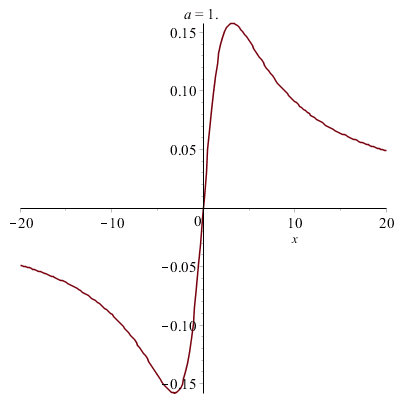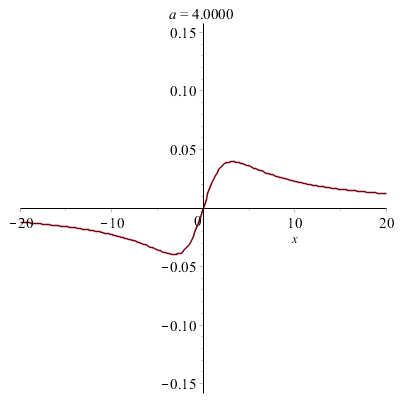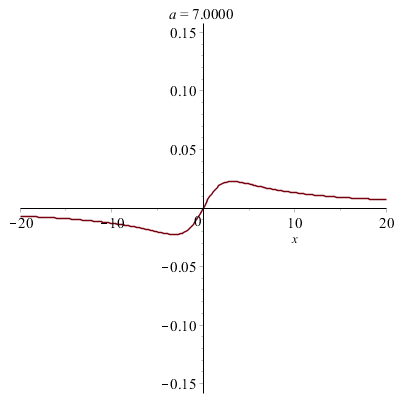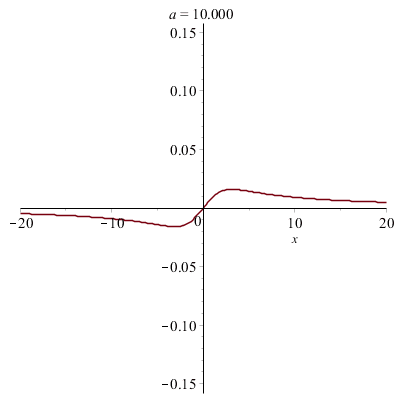
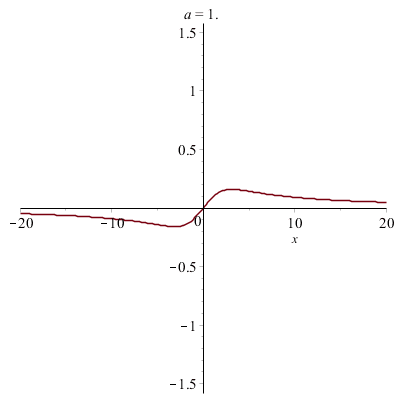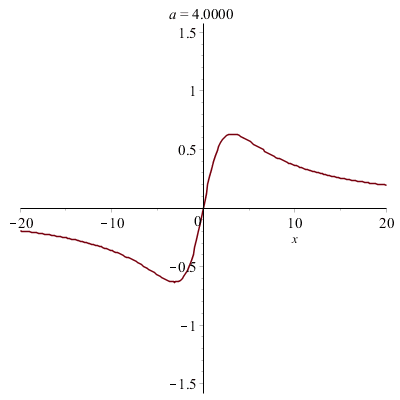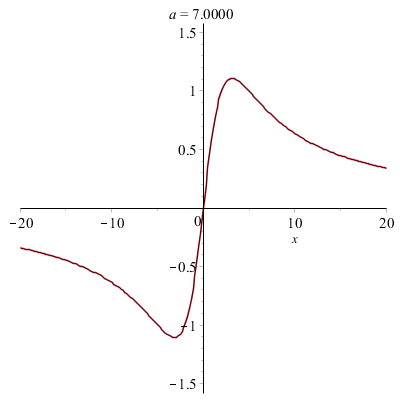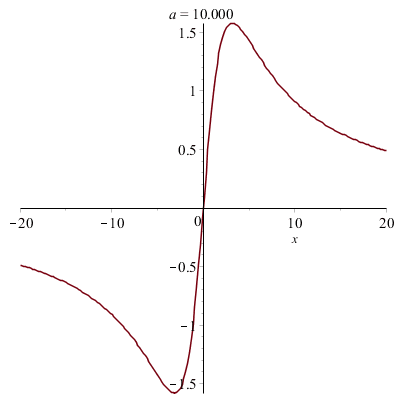
Courbes paramétrées

On peut tracer des courbes paramétrées. Attention, il faut bien placer les crochets...

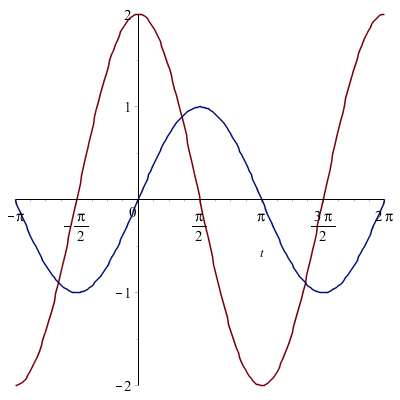
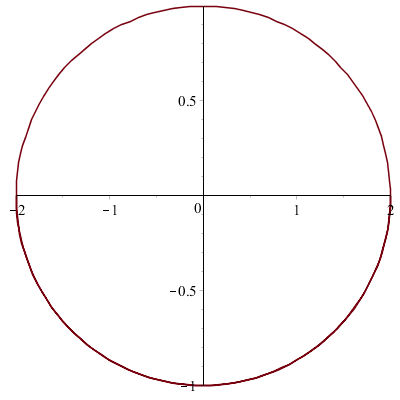
On a l'impression de voir un cercle... En fait c'est une ellipse :

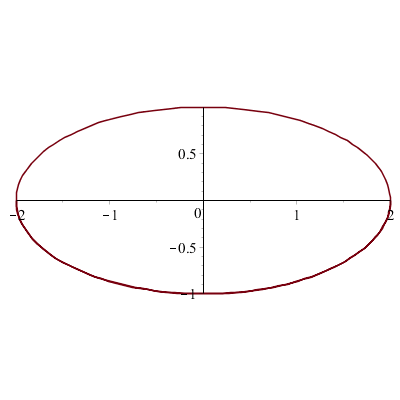
Avec les fonctions hyperboliques, on peut tracer... des hyperboles !

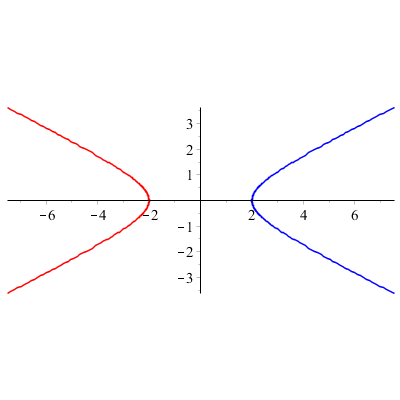
Une courbe paramétrée intéressante :

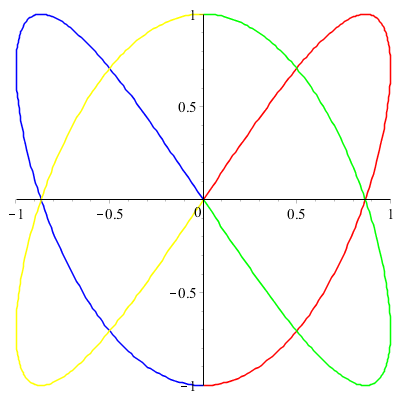
Version dynamique :

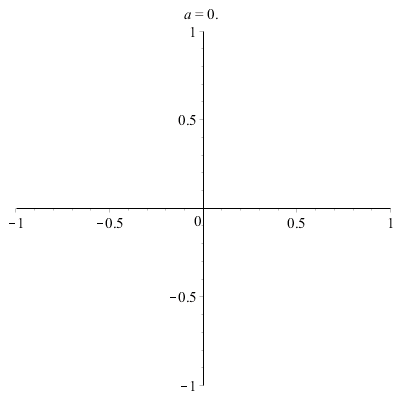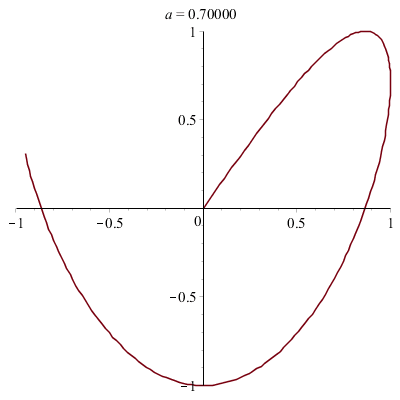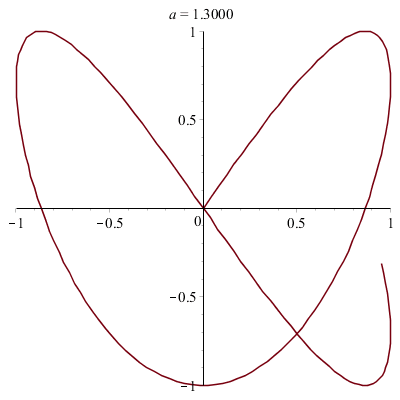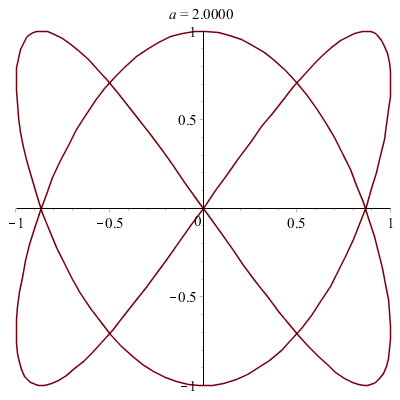
Il s'agit d'une courbe de Lissajous (encore baptisée Lemniscate de Gerono) observée sur un oscilloscope (étude conjointe de deux ondes sinusoïdales).

Une autre courbe paramétrée intéressante :

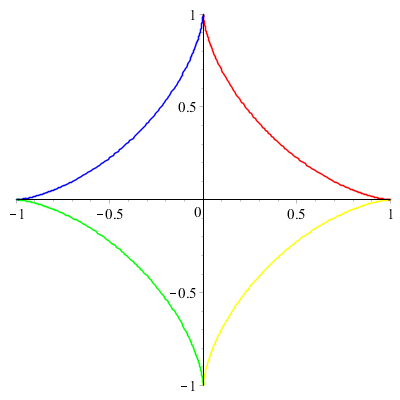
Porte coulissant le long de deux glissières perpendiculaires (porte de garage) :

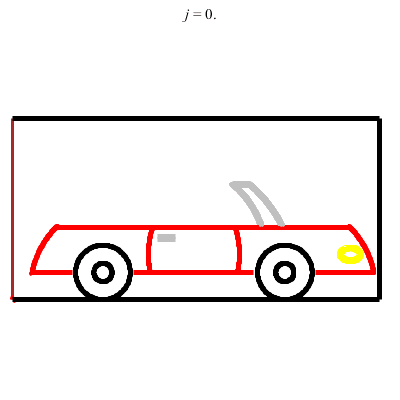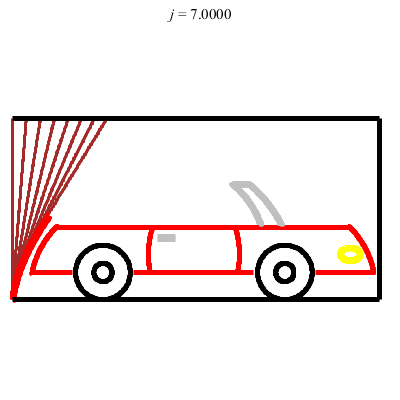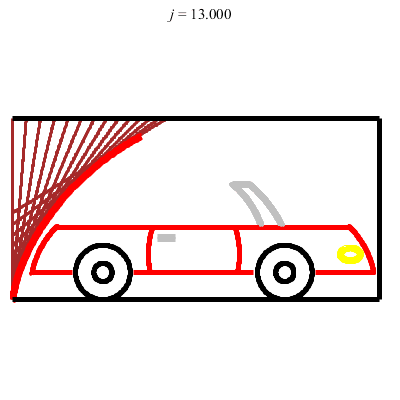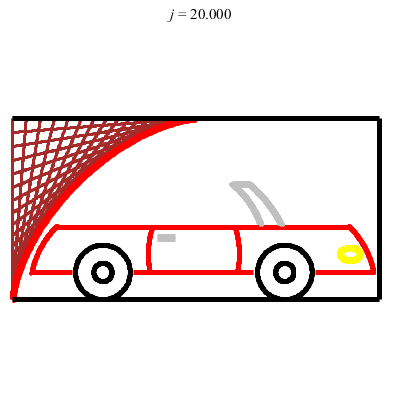
Touche pas à mon coffre !

On linéarise X(t) et Y(t) :

Et l'on découvre une hypocycloïde importante : l'astroïde ! (trajectoire d'un point situé sur un cercle roulant à l'intérieur d'un cercle quatre fois plus grand sans glissement)

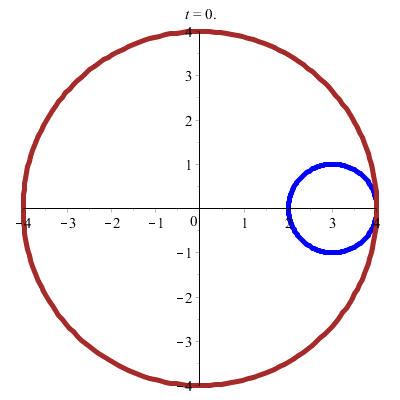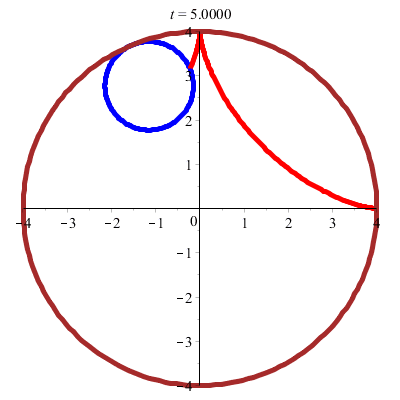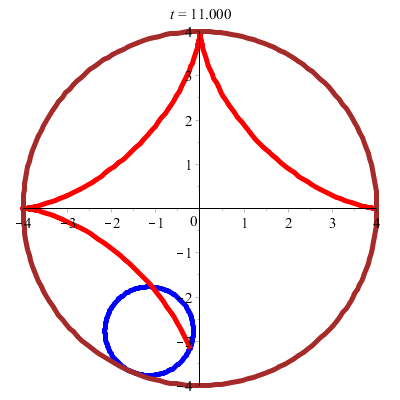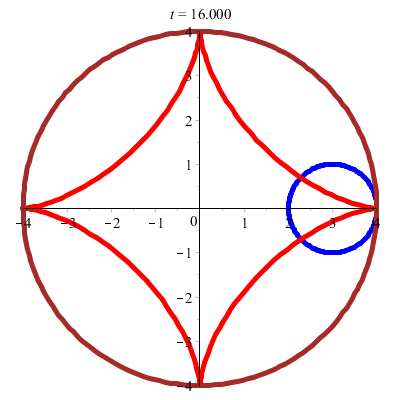
Courbes polaires

Une courbe en coordonnées polaires ρ=f(θ) s'étudie par le biais d'une courbe paramétrée x = f(θ) cos(θ), y = f(θ) sin(θ).

Quelques spirales :

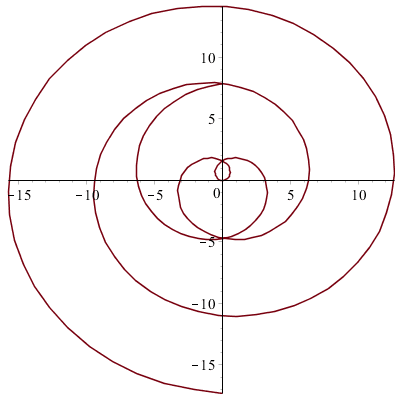
C'est la spirale d'Archimède.

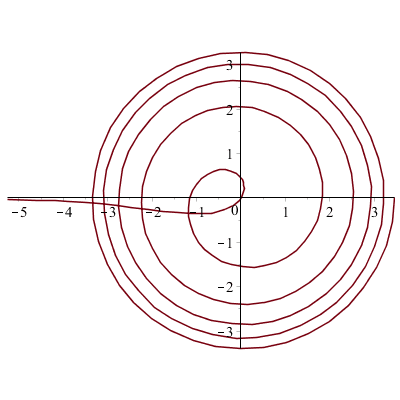
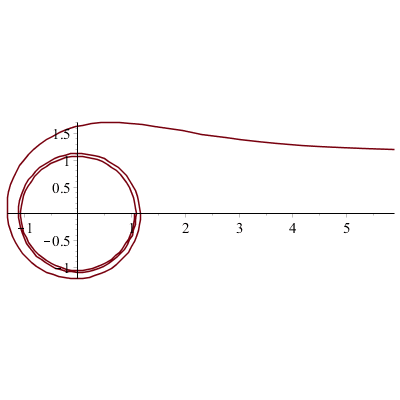
Quelques rosaces :

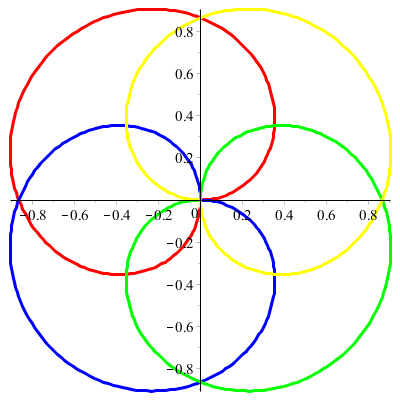
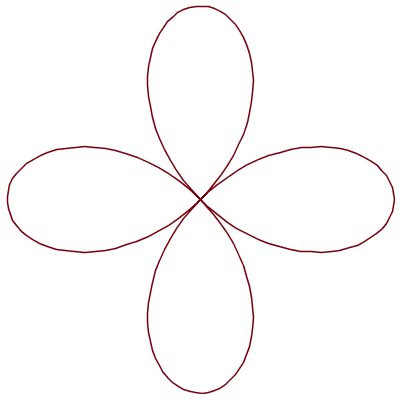
Courbes implicites

Une ellipse :

Une hyperbole :

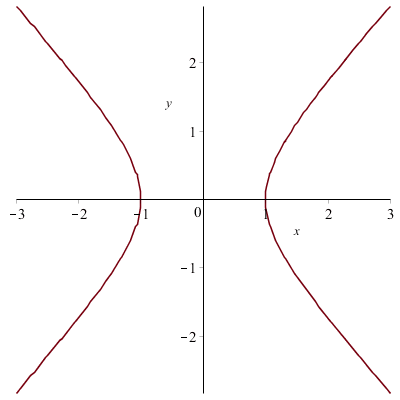
Le folium de Descartes :

... et la lemniscate de Bernoulli :

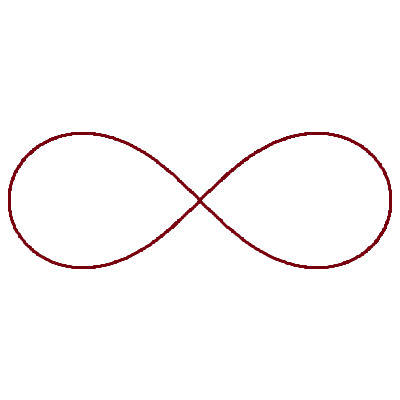
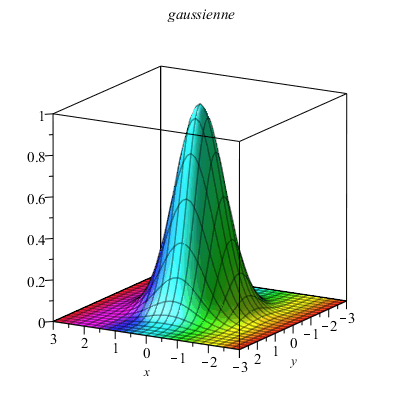
Quelques surfaces : gaussienne, quadriques...

Maple peut aussi faire de très beaux dessins en 3D... On peut tracer des surfaces.

La gaussienne standard :

Un paraboloïde elliptique :

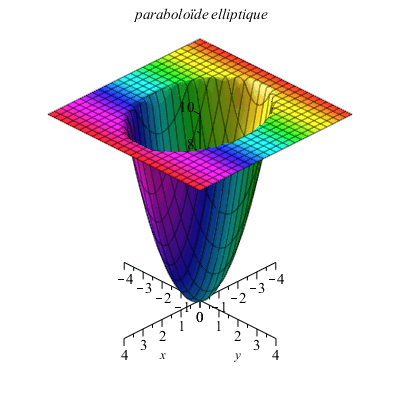
... et un paraboloïde hyperbolique :

Un ellipsoïde de révolution :

... et un hyperboloïde à une nappe :