V. Procédures



Cordes vibrantes et séries de Fourier

Équation des ondes :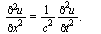
La quantité u(x,t) représente la forme de la corde à l'instant t, à la position x.
On peut écrire une procédure pour illustrer le mouvement de la corde à l'aide d'animations.
Corde vibrante pincée (e.g. d'une guitare) :










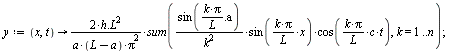
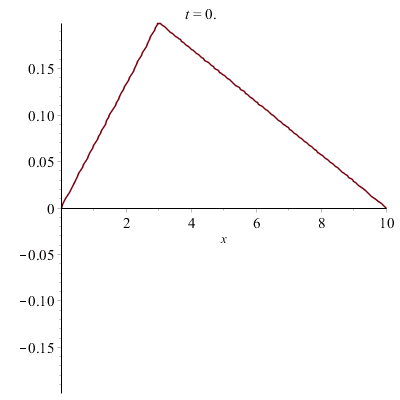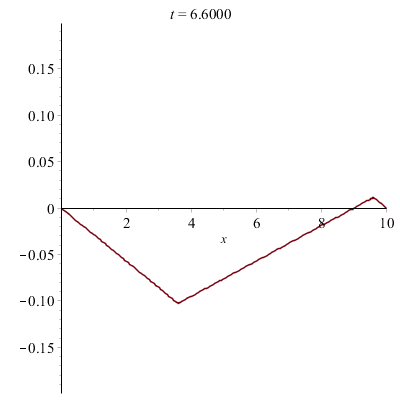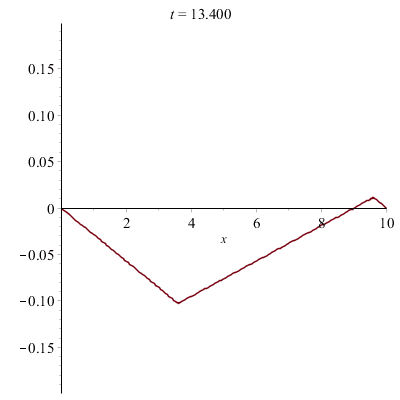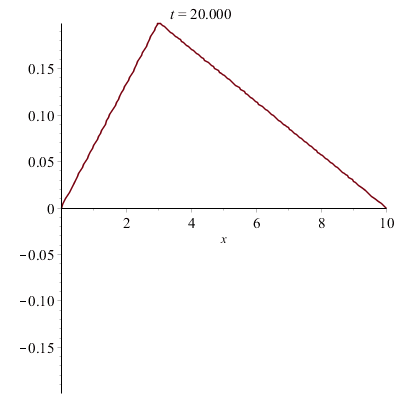
La corde a été pincée avec un médiator. En la pinçant sans médiator exactement au milieu :






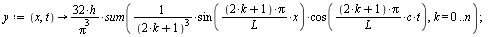
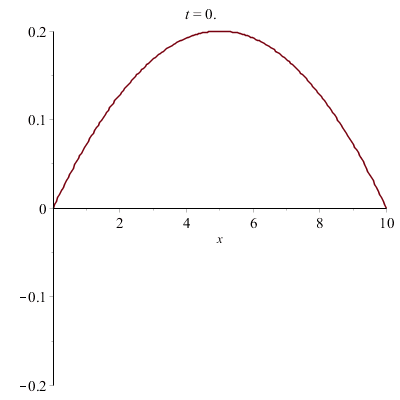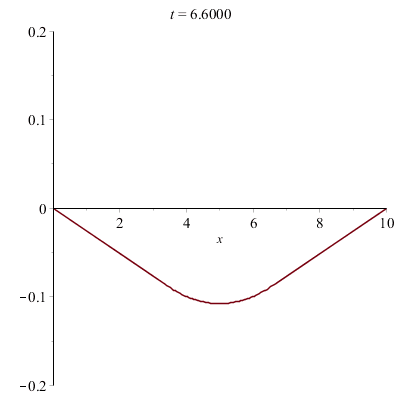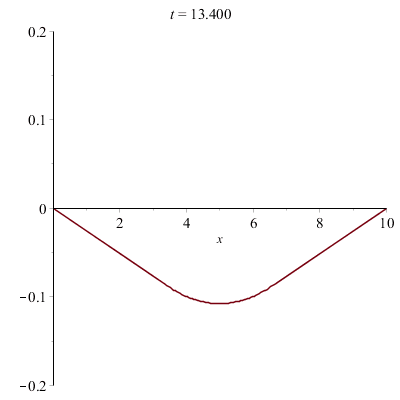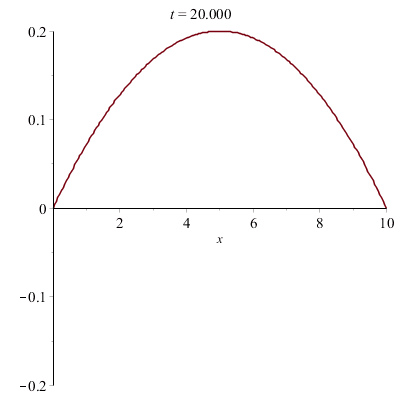
Corde vibrante frappée (e.g. d'un piano) :










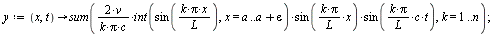
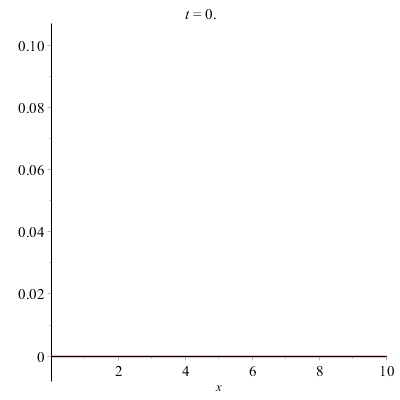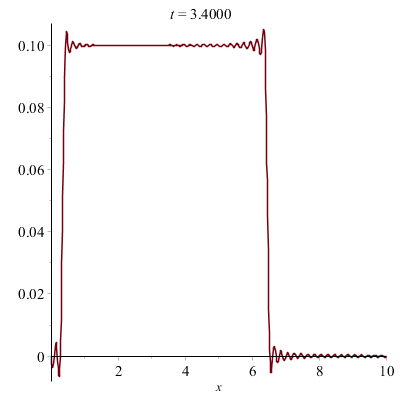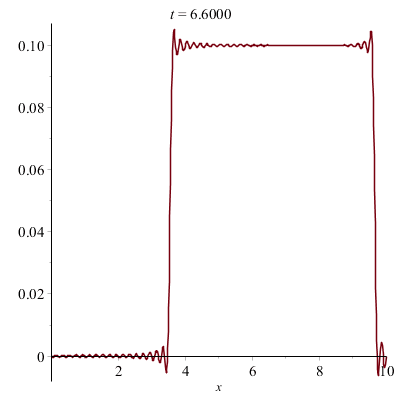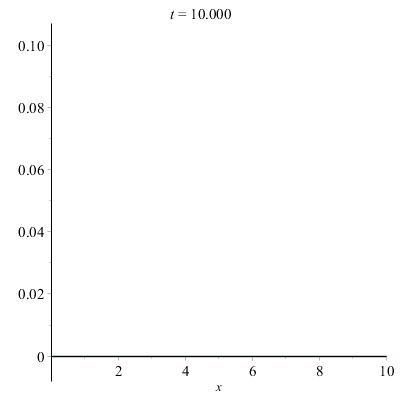
Ensembles de Julia

Pour chaque c = c1+ic2, on définit l'ensemble des points x0+iy0 tels que la suite de points démarrant de z0 = x0+iy0 et vérifiant zn+1 = zn2+c soit bornée (et lorsque c'est le cas, elle est bornée en module par 2) :























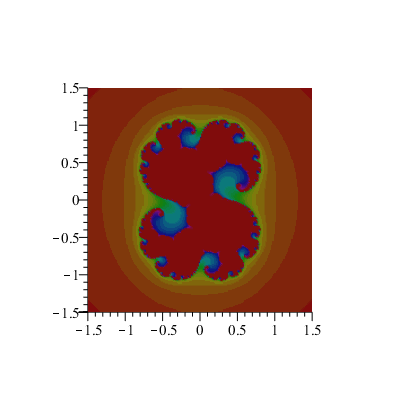
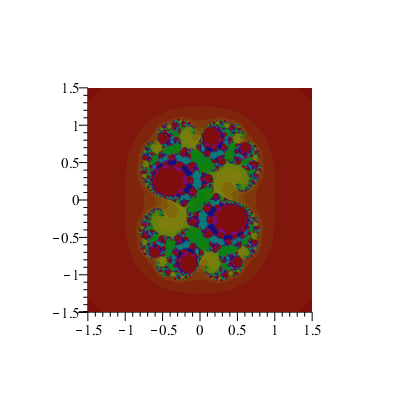
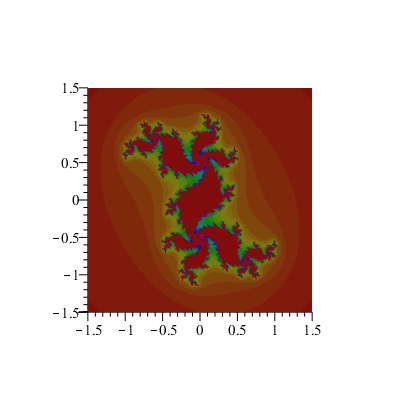
À chaque point (a,b) de la grille [–1.5;1.5]x[–1.5;1.5], on associe un niveau de couleur correspondant au nombre d'itérations <N telles que la suite soit bornée.

Une valeur de c et quelques valeurs de N :























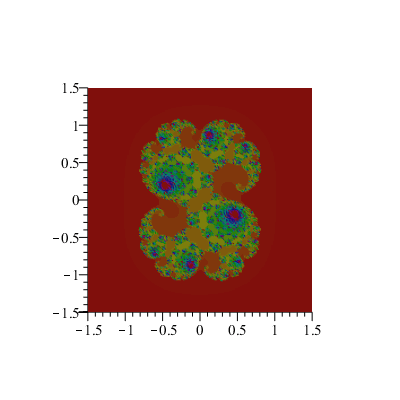
D'autres valeurs de c :

















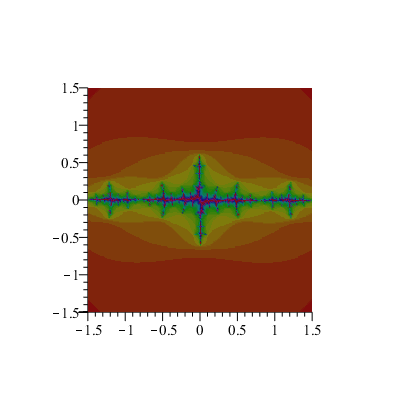
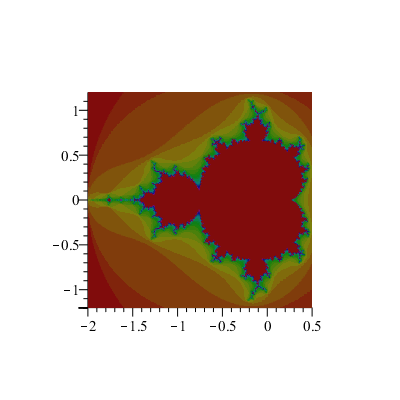
Ensemble de Mandelbrot

C'est l'ensemble des points c tels que la suite de points démarrant de z0 et vérifiant zn+1 = zn2+c soit bornée :














   
◄ Sommaire ►