Summaries of the papers listed here

Testing copula-based dependence hypotheses: a proofreading based on functional decompositions

Tests of multivariate independence may rely on asymptotically independent Cramér-von Mises statistics derived from a Möbius decomposition of the empirical copula process. We generalize this approach to some other copula-based assumptions, with the help of a functional decomposition based on commuting idempotent maps. As soon as the null hypothesis reflects the stability of the copula under the action of the composition of such operators, the methodology applies. The asymptotic joint distribution of the terms in the decomposition of the empirical copula process is established under the null hypothesis. Since the latter depends on the unknown copula being tested, we adapt the subsampling procedure to our setting and recall that the multiplier bootstrap as well as the parametric bootstrap also apply to approximate p-values. The benefit in deriving test statistics from a functional decomposition, defined in accordance with the dependence assumption under study, is illustrated and discussed through simulations.

Linking the Hoeffding--Sobol and Möbius formulas through a decomposition of Kuo, Sloan, Wasilkowski, and Wozniakowski

Extensions of a result of Kuo, Sloan, Wasilkowski, and Woźniakowski (2010) are presented which unify the derivation of the Hoeffding–Sobol and Möbius decompositions of a multivariate function as a sum of terms of increasing complexity.

Hoeffding--Sobol decomposition of homogeneous co-survival functions: from Choquet representation to extreme value theory application

The paper investigates the Hoeffding--Sobol decomposition of homogeneous co-survival functions. For this class, the Choquet representation is transferred to the terms of the functional decomposition, and in addition to their individual variances, or to the superset combinations of those. The domain of integration in the resulting formulae is reduced in comparison with the already known expressions. When the function under study is the stable tail dependence function of a random vector, ranking these superset indices corresponds to cluster the components of the random vector with respect to their asymptotic dependence. Their Choquet representation is the main ingredient in deriving a sharp upper bound for the quantities involved in the tail dependograph, a graph in extreme value theory that summarizes asymptotic dependence.

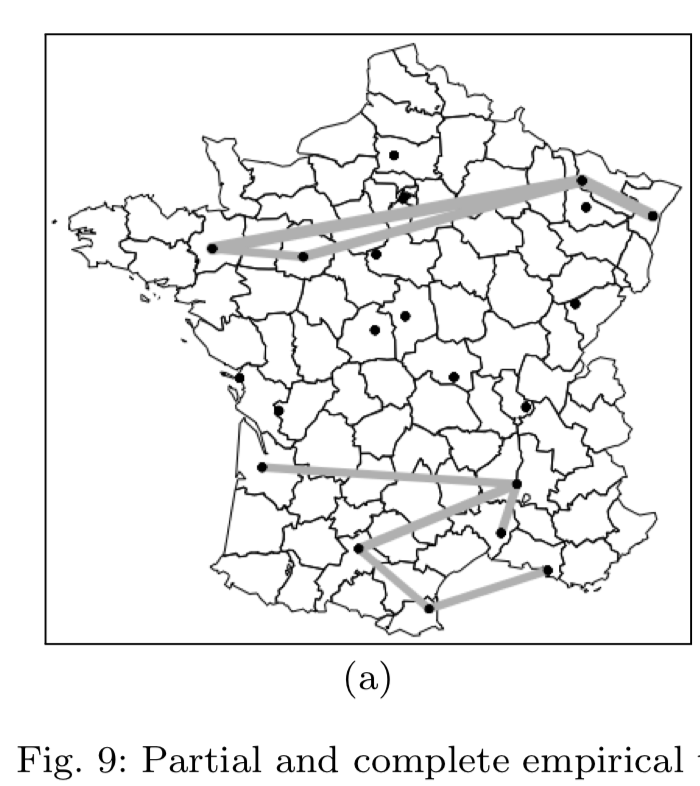
The tail dependograph

Modeling extreme rainfall: A comparative study of spatial extreme value models

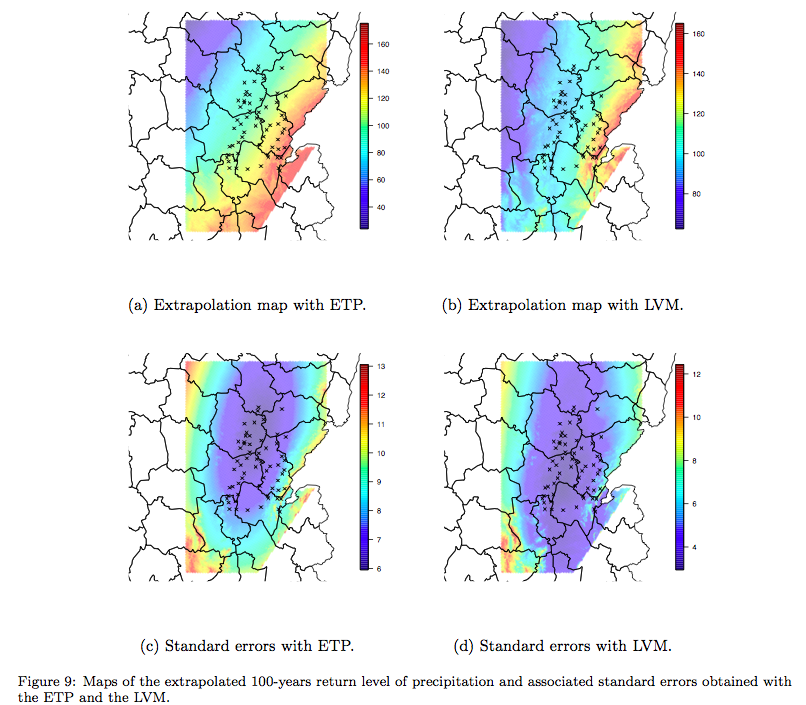
In this paper, focus is done on spatial models for extreme events and on their respective efficiency regarding the estimation of two risk measures: one extrapolating marginal distributions and one summarizing the spatial bivariate dependence of extremes. A wide comparison is performed on a simulation plan that has been specifically designed from a daily precipitation data set. The objective of this paper is twofold: firstly, pointing out the inherent properties of each model, and secondly, advising users on how to choose the model depending on the specific type of risk.

A standardized distance-based index to assess the quality of space-filling designs

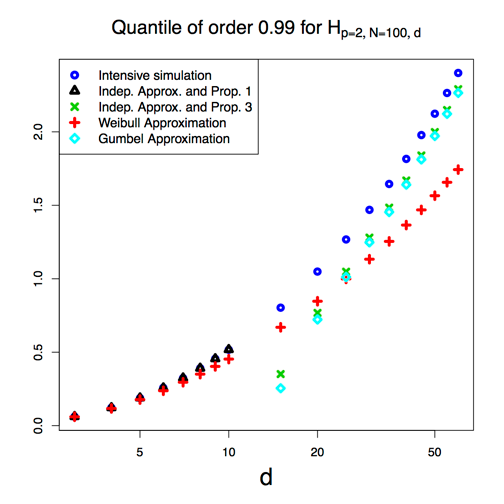
One of the most used criterion for evaluating space-filling design in computer experiments is the minimal distance between pairs of points. The focus of this paper is to propose a normalized quality index that is based on the distribution of the minimal distance when points are drawn independently from the uniform distribution over the unit hypercube. Expressions of this index are explicitly given in terms of polynomials under any \(L^p\) distance. When the size of the design or the dimension of the space is large, approximations relying on extreme value theory are exhibited. Some illustrations of our index are presented on simulated data and on a real problem.

Adapting extreme value statistics to financial time series: dealing with bias and serial dependence

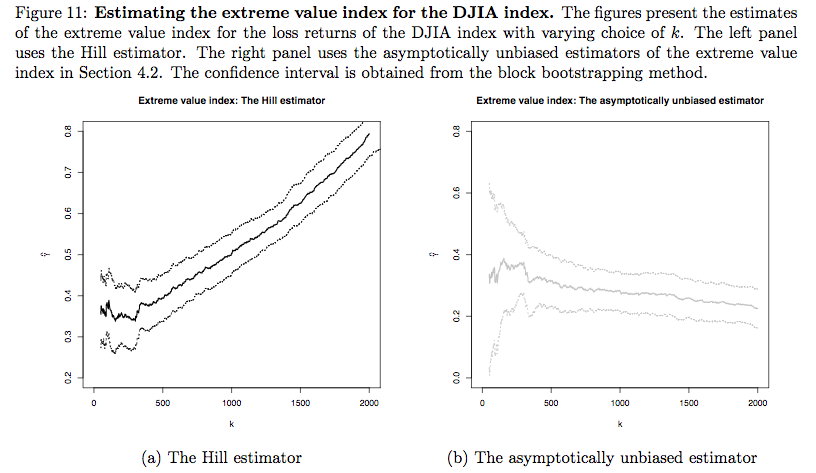We handle two major issues in applying extreme value analysis to financial time series, bias and serial dependence, jointly. This is achieved by studying bias correction method when observations exhibit weakly serial dependence, namely the \(\beta\)-mixing series. For estimating the extreme value index, we propose an asymptotically unbiased estimator and prove its asymptotic normality under the \(\beta\)-mixing condition. The bias correction procedure and the dependence structure have a joint impact on the asymptotic variance of the estimator. Then, we construct an asymptotically unbiased estimator of high quantiles. We apply the new method to estimate the Value-at-Risk of the daily return on the Dow Jones Industrial Average Index.

Bias correction in multivariate extremes

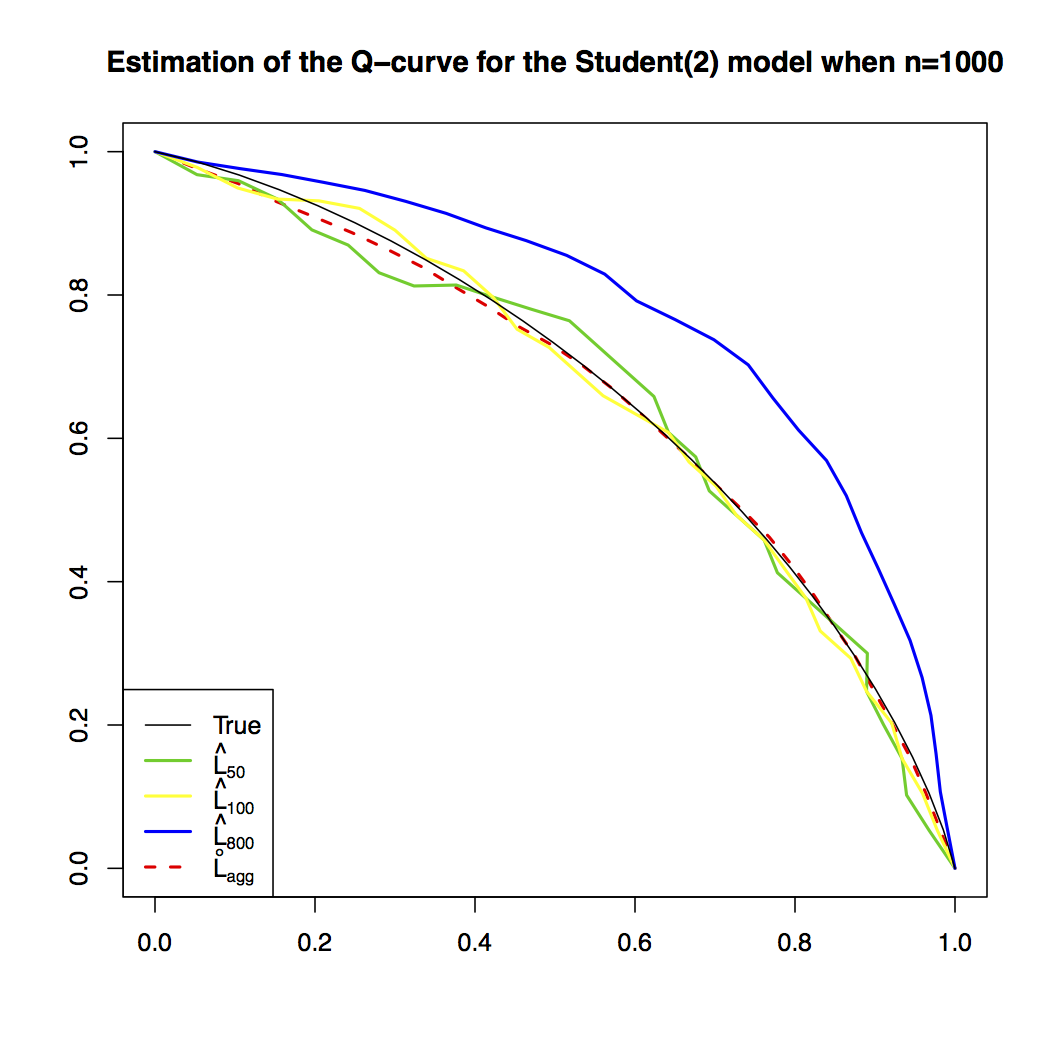
The estimation of the extremal dependence structure is spoiled by the impact of the bias, which increases with the number of observations used for the estimation. Already known in the univariate setting, the bias correction procedure is studied in this paper under the multivariate framework. New families of estimators of the stable tail dependence function are obtained. They are asymptotically unbiased versions of the empirical estimator introduced by Huang [Statistics of bivariate extremes (1992) Erasmus Univ.]. Since the new estimators have a regular behavior with respect to the number of observations, it is possible to deduce aggregated versions so that the choice of the threshold is substantially simplified. An extensive simulation study is provided as well as an application on real data.

Environmental data: multivariate Extreme Value Theory in practice

Let \((X_t,Y_t)\) be a bivariate stationary time series in some environmental study. We are interested to estimate the failure probability defined as \(\mathbb{P}(X_t > x,Y_t > y)\), where \(x\) and \(y\) are high return levels. For the estimation of high return levels, we consider three methods from univariate extreme value theory, two of which deal with the extreme clusters. We further derive estimators for the bivariate failure probability, based on Draisma et al. (2004)’s approach and on Heffernan and Tawn (2004)’s approach. The comparison on different estimators is demonstrated via a simulation study. To the best of our knowledge, this is the first time that such a comparative study is performed. Finally, we apply the procedures to the real data set and the results are discussed.

Dense classes of multivariate extreme value distributions

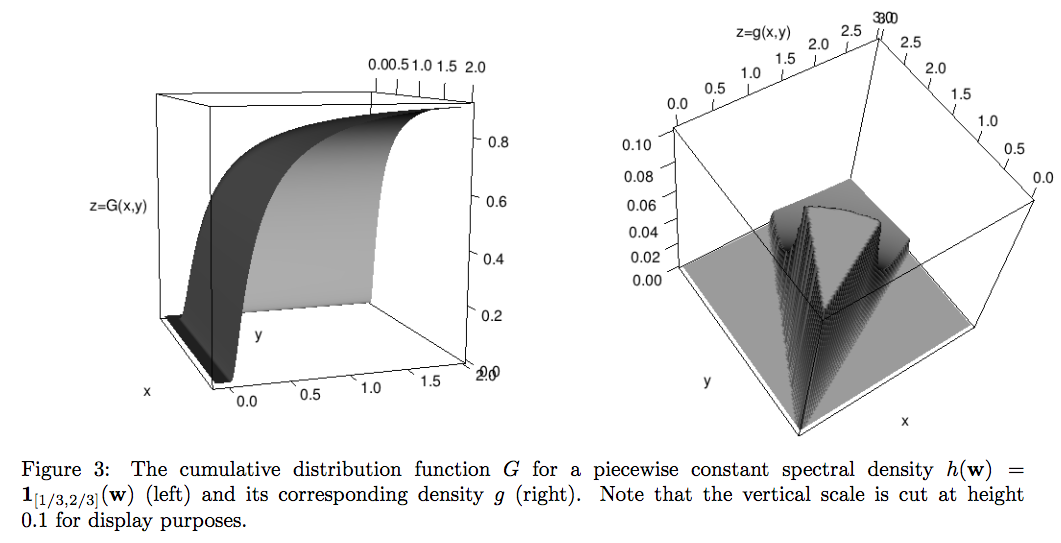In this paper, we explore tail dependence modelling in multivariate extreme value distributions. The measure of dependence chosen is the scale function, which allows combinations of distributions in a very exible way. The correspondences between the scale function and the spectral measure or the stable tail dependence function are given. Combining scale functions by simple operations, three parametric classes of laws are (re)constructed and analyzed, and resulting nested and structured models are discussed. Finally, the denseness of each of these classes is shown.

Optimal rates of convergence in the Weibull model based on kernel-type estimators

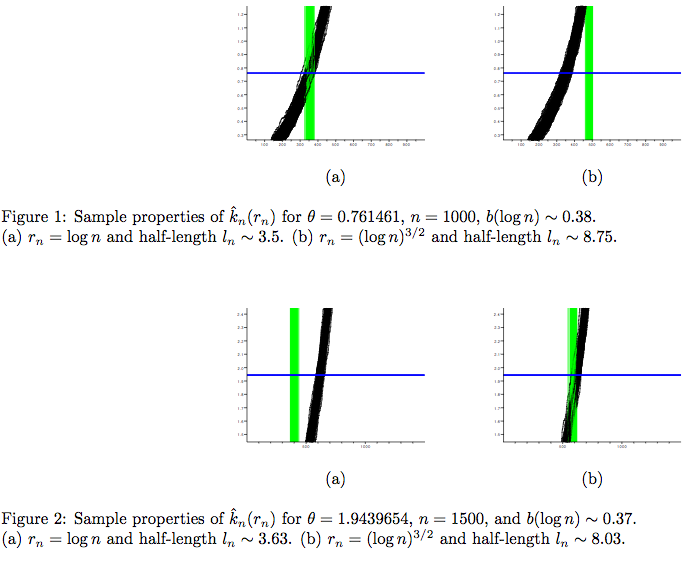
Let \(F\) be a distribution function in the maximal domain of attraction of the Gumbel distribution and such that \(-\log(1-F(x))=x^{1/\theta}L(x)\) for a positive real number \(\theta\), called the Weibul tail index, and a slowly varying function \(L\). It is well known that the estimators of \(\theta\) have a very slow rate of convergence. We establish here a sharp optimality result in the minimax sense, that is when \(L\) is treated as an in nite dimensional nuisance parameter belonging to some functional class. We also establish the rate optimal asymptotic property of a data-driven choice of the sample fraction that is used for estimation.

Risk measures and multivariate extensions of Breiman’s theorem

Modeling insurance risks is a task that received an increasing attention because of Solvency Capital Requirements. The ruin probability has become a standard risk measure to assess regulatory capital. In this paper we focus on discrete time models for finite time horizon. Several results are available in the literature allowing to calibrate the ruin probability by means of the sum of the tail probabilities of individual claim amounts. The aim of this work is to obtain asymptotics for such probabilities under multivariate regularly variation and, more precisely, to derive them from Breiman’s Theorem extensions. We thus exhibit new situations where the ruin probability admits computable equivalents. Consequences are also derived in terms of the Value-at-Risk.

Semi-parametric estimation for heavy tailed distributions

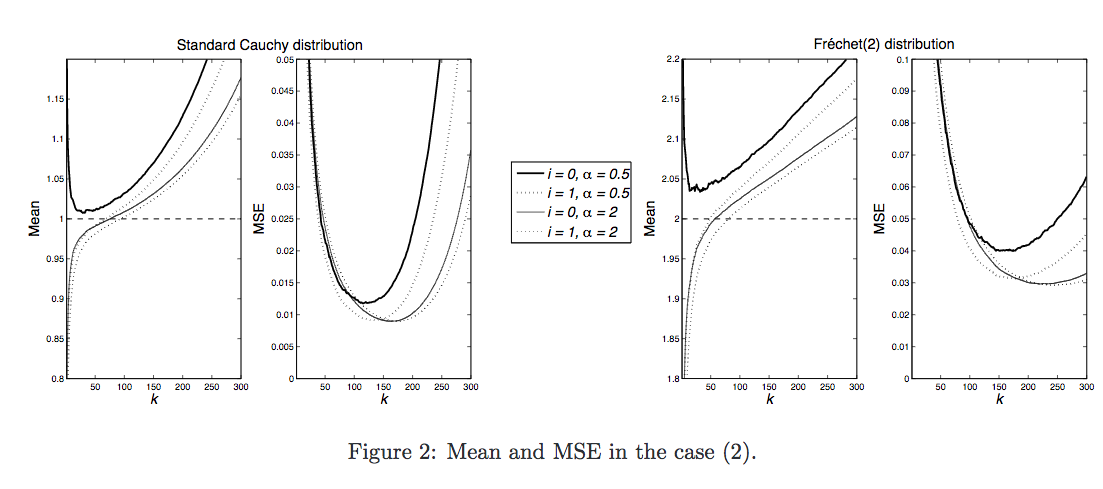In this paper, we generalize several works in the extreme value theory for the estimation of the extreme value index and the second order parameter. Weak consistency and asymptotic normality are proven under classical assumptions. Some numerical simulations and computations are also performed to illustrate the finite-sample and the limiting behavior of the estimators.

GNSS Integrity Achievement by using Extreme Value theory

The demonstration of the GNSS integrity requirement (\(10^{-7}\)/150 sec range) for SBAS services as for future systems like GALILEO is a key issue either in the development/acceptance phase or in the operational one. Currently, for SBAS as EGNOS or WAAS, a lot of simulations coupled with data collections were done before the operation or service commissioning and a permanent data collection network is used to monitor, among other parameters, the integrity (or more precisely the absence of a Loss Of Integrity (LOI) in case of misleading information). The demonstration needs to assess a \(10^{-7}\) order of magnitude which is a tricky issue: the classical methods require several tens years of observations and such LOI are generally not observed among the data because of their scarcity. To make possible the extrapolation of the error distributions into the tails, CNES and TAS have established a research action with French Universities of Lyon I and Toulouse III to use the Extreme Value Theory (EVT). Recent developments in quantile estimation have allowed the application of EVT in numerous domains regardless of the underlying error distributions of the measurement data, and avoid the questionable assumption of Gaussian error distributions. …

The likelihood ratio test for general mixture models with possibly structural parameter

This paper deals with the likelihood ratio test (LRT) for testing hypotheses on the mixing measure in mixture models with or without structural parameter. The main result gives the asymptotic distribution of the LRT statistics under some conditions that are proved to be almost necessary. A detailed solution is given for two testing problems: the test of a single distribution against any mixture, with application to Gaussian, Poisson and binomial distributions; the test of the number of populations in a finite mixture with or without structural parameter

Numerical bounds for the distribution of the maximum of one- and two-dimensional processes

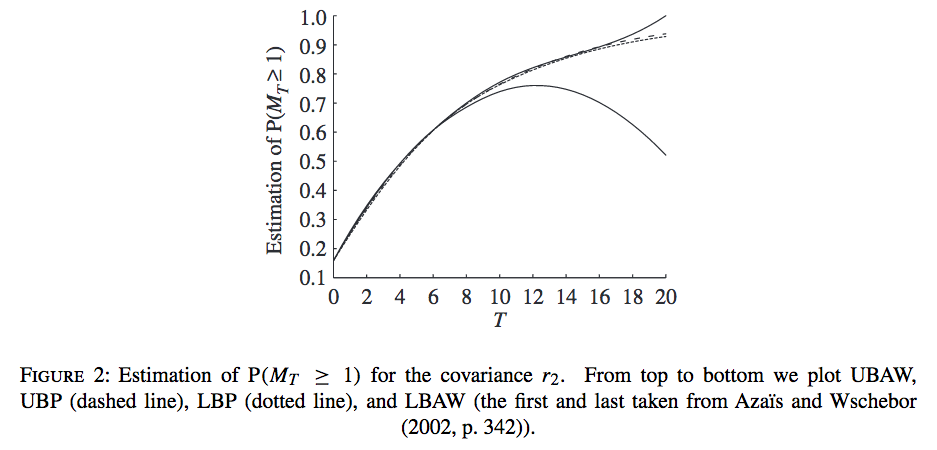We consider the class of real-valued stochastic processes indexed on a compact subset of \(\mathbb{R}\) or \(\mathbb{R}^2\) with almost surely absolutely continuous sample paths. We obtain an implicit formula for the distributions of their maxima. The main result is the derivation of numerical bounds that turn out to be very accurate, in the Gaussian case, for levels that are not large. We also present the first explicit upper bound for the distribution tail of the maximum in the two-dimensional Gaussian framework. Numerical comparisons are performed with known tools such as the Rice upper bound and expansions based on the Euler characteristic. We deal numerically with the determination of the persistence exponent.

{MAGP Toolbox}

Asymptotic distribution and local power of the likelihood ratio test for mixtures

We consider the log-likelihood ratio test (LRT) for testing the number of components in a mixture of populations in a parametric family. We provide the asymptotic distribution of the LRT statistic under the null hypothesis as well as under contiguous alternatives when the parameter set is bounded. Moreover, for the simple contamination model we prove, under general assumptions, that the asymptotic local power under contiguous hypotheses may be arbitrarily close to the asymptotic level when the set of parameters is large enough. In the particular problem of normal distributions, we prove that, when the unknown mean is not a priori bounded, the asymptotic local power under contiguous hypotheses is equal to the asymptotic level.

Asymptotic poisson character of extremes in non-stationary Gaussian models

Let \(X\) be a non-stationary Gaussian process, asymptotically centered with constant variance. Let \(u\) be a positive real. Define \(R_u(t)\) as the number of upcrossings of level \(u\) by the process \(X\) on the interval \((0, t]\). Under some conditions we prove that the sequence of point processes \((R_u)_{u>0}\) converges weakly, after normalization, to a standard Poisson process as u tends to infinity. In consequence of this study we obtain the weak convergence of the normalized supremum to a Gumbel distribution.