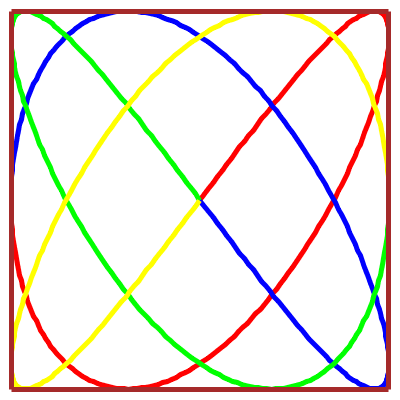
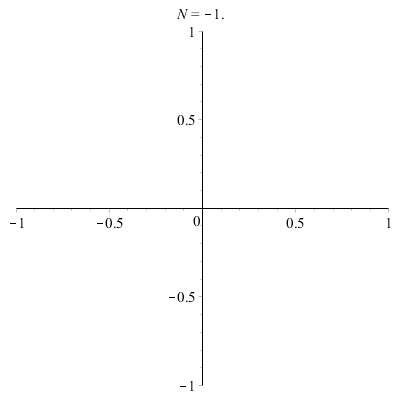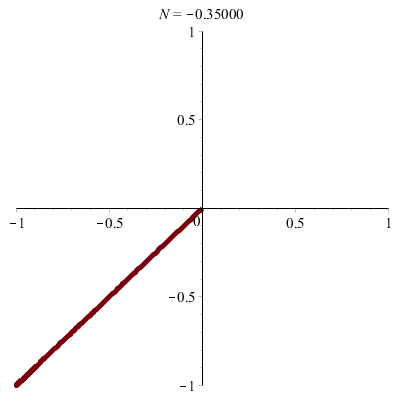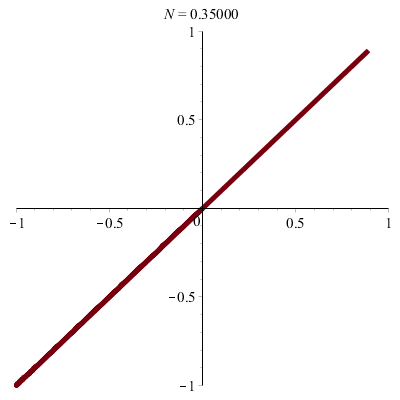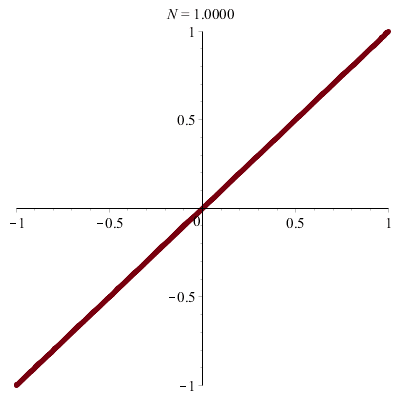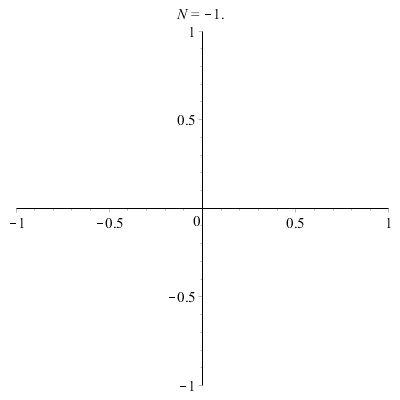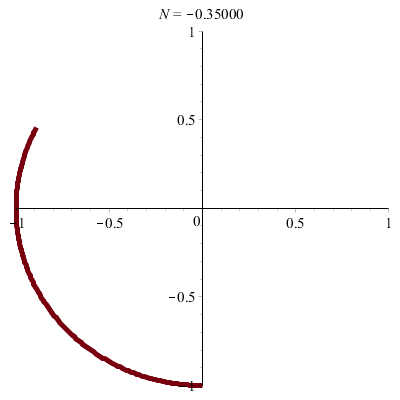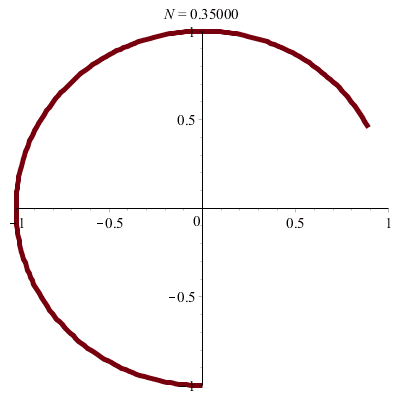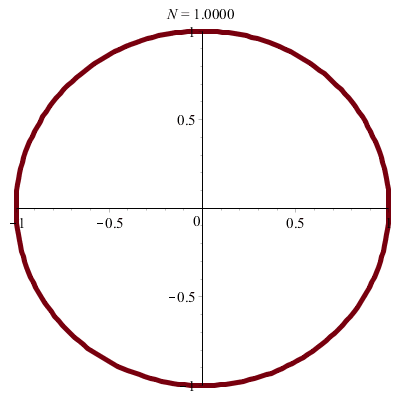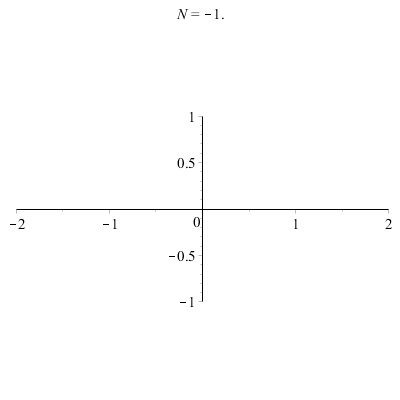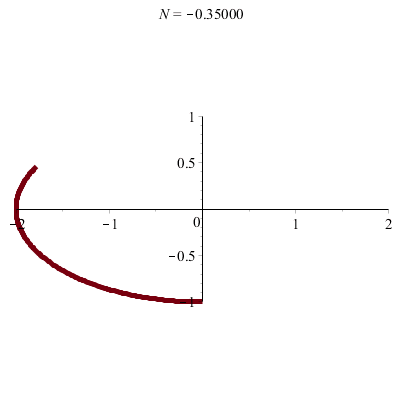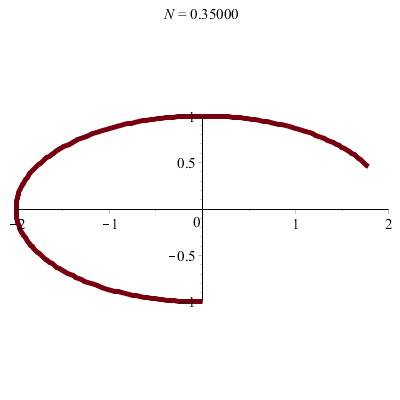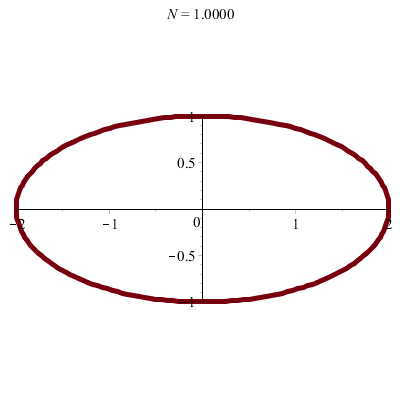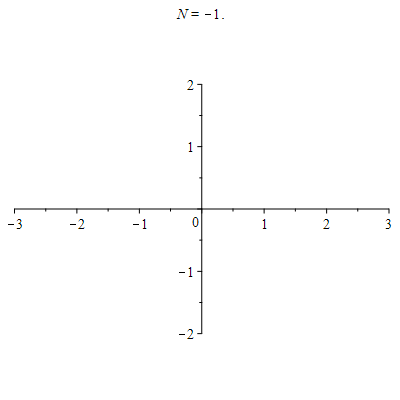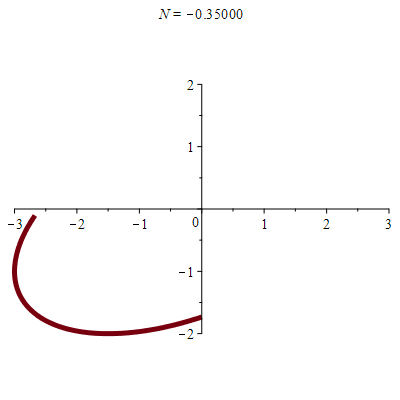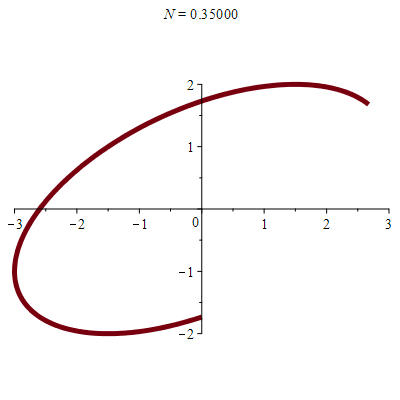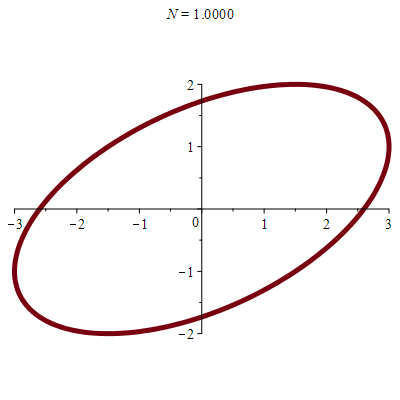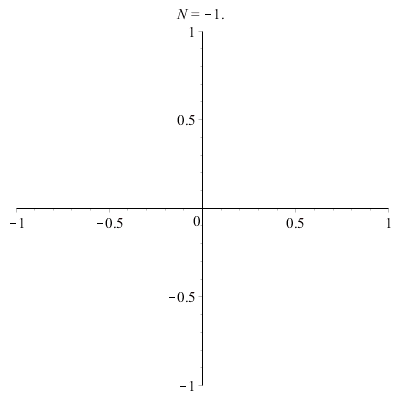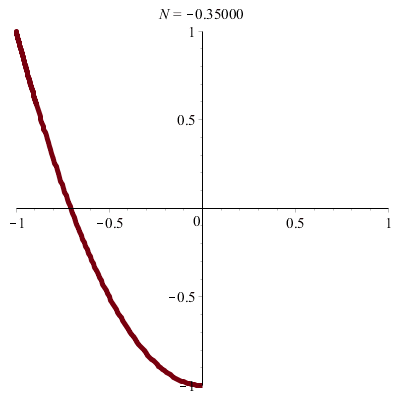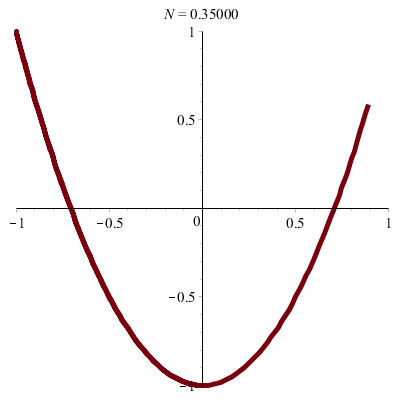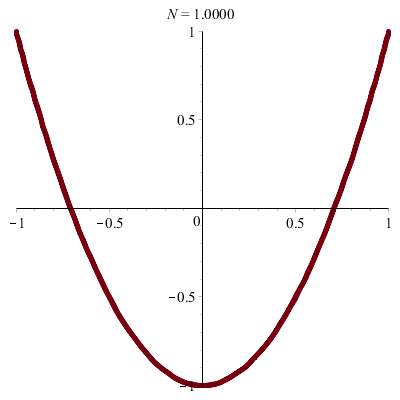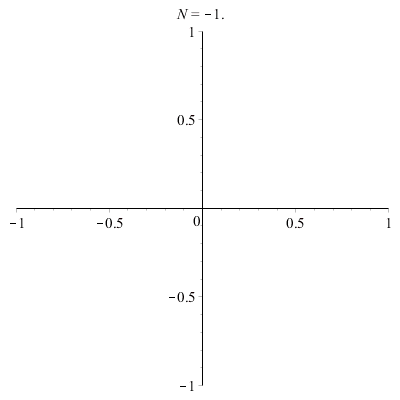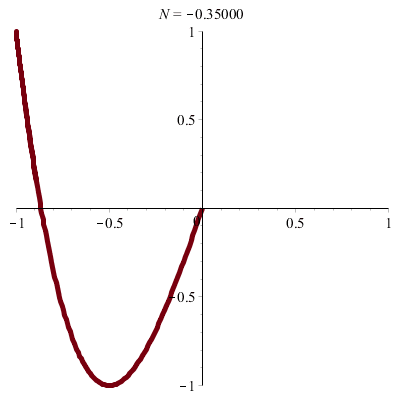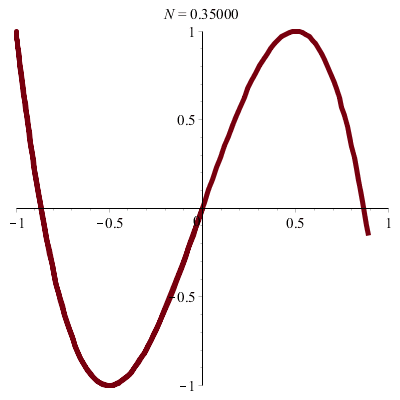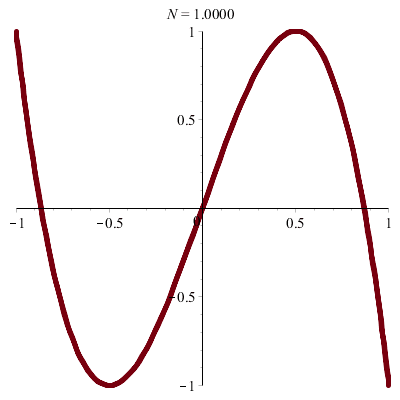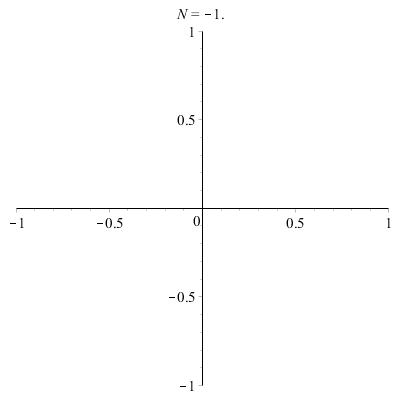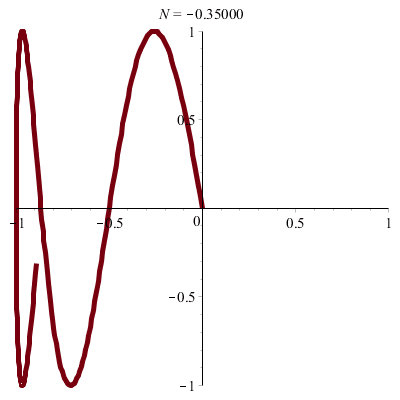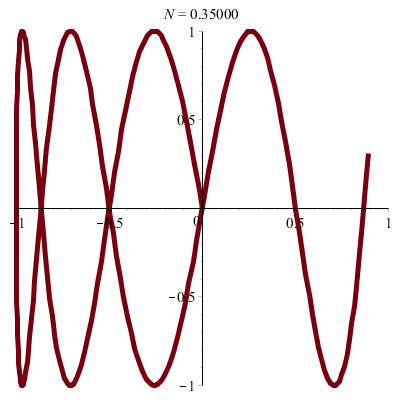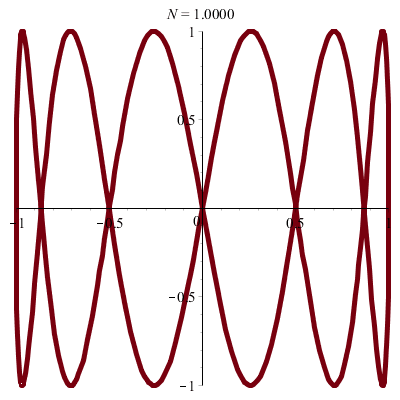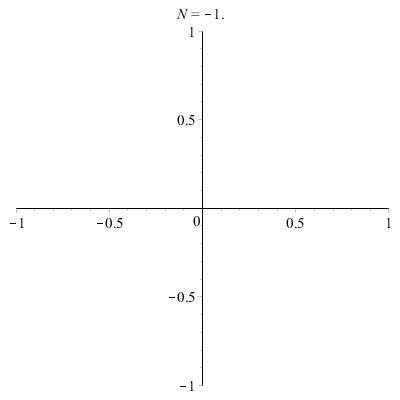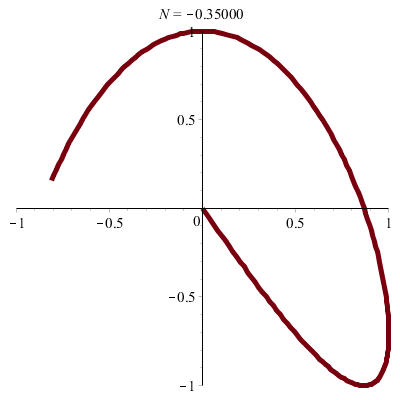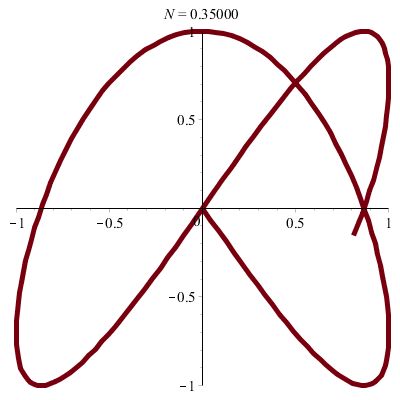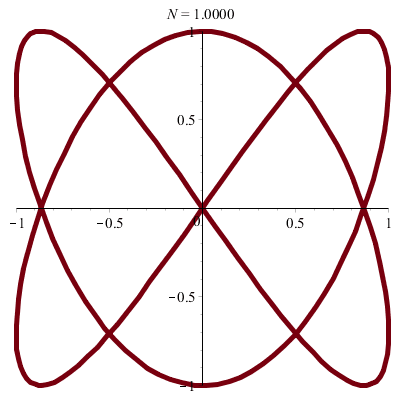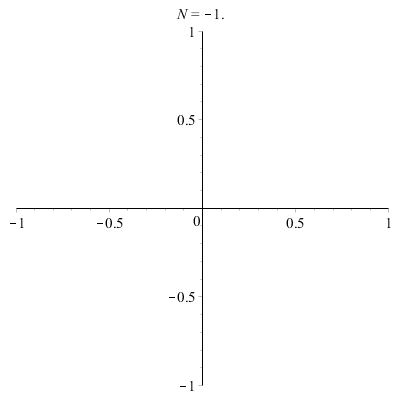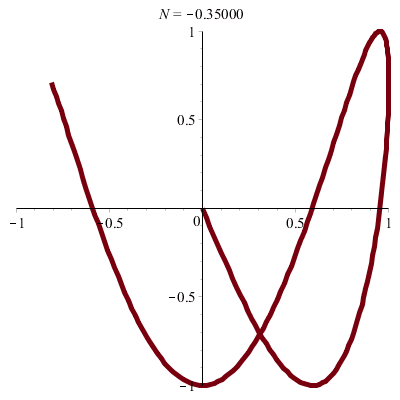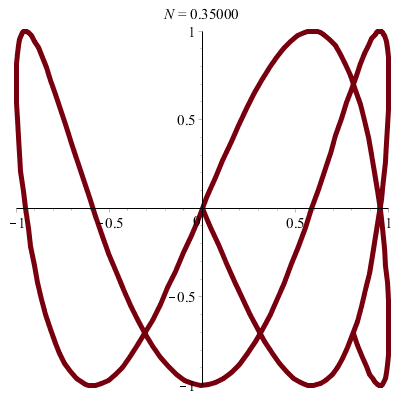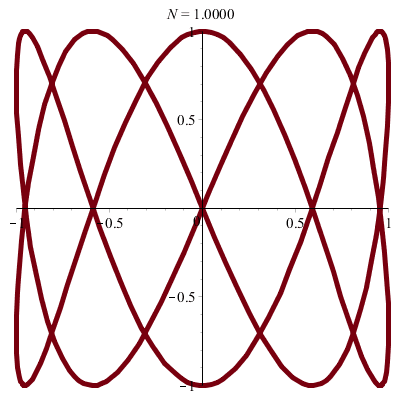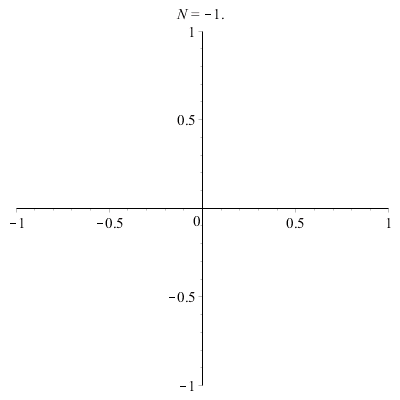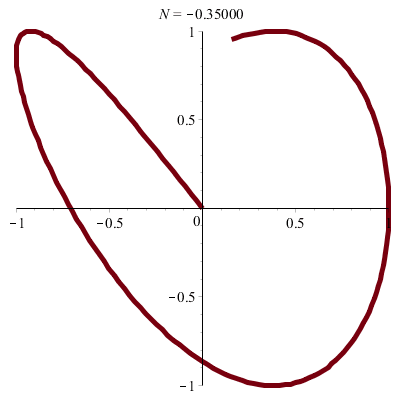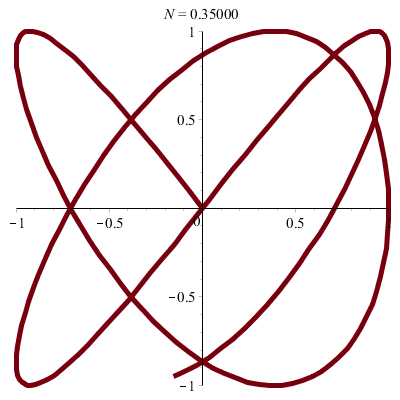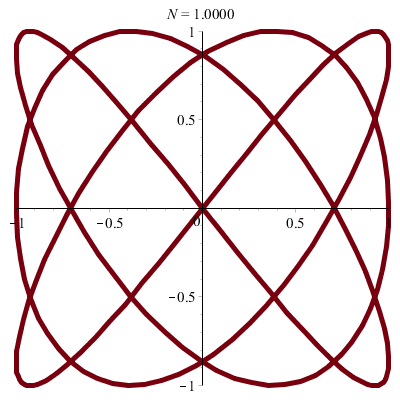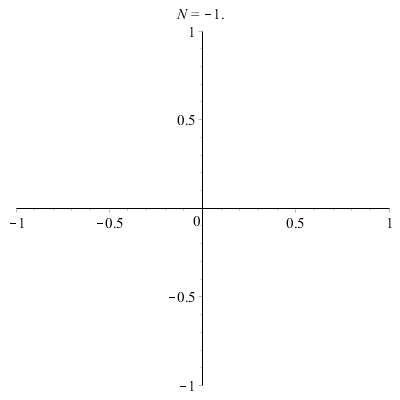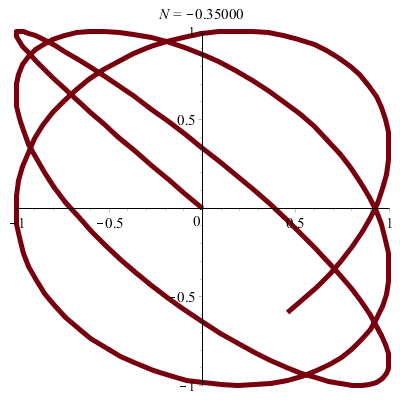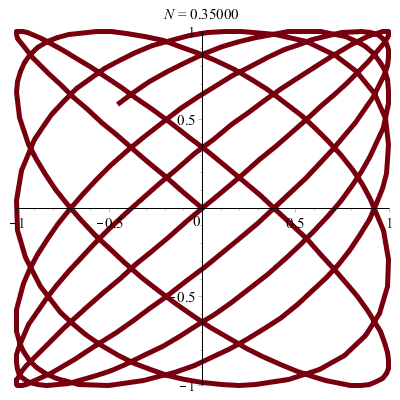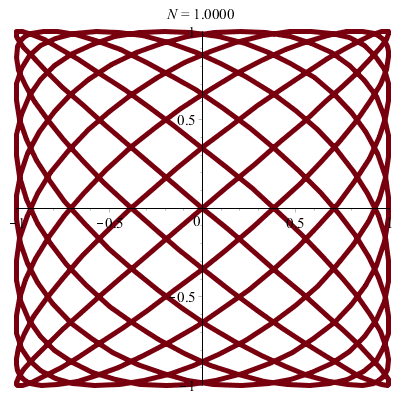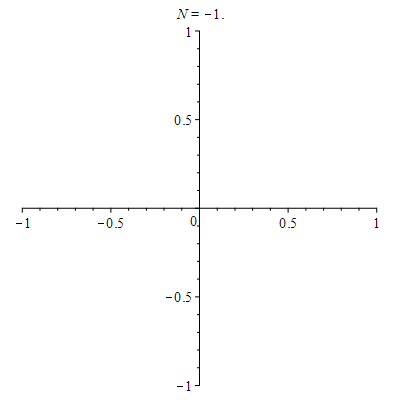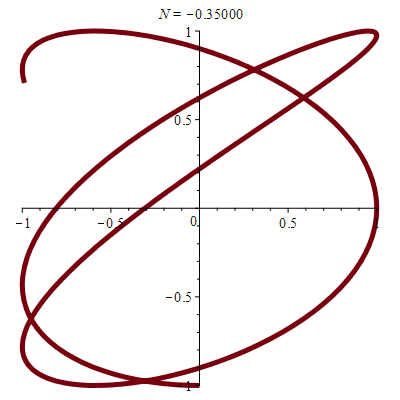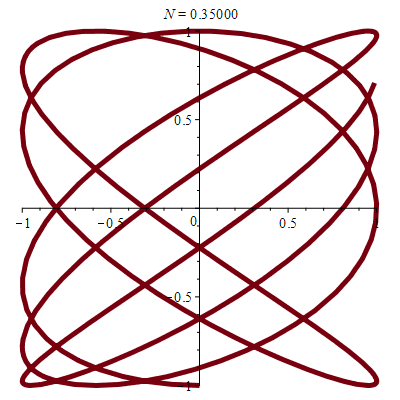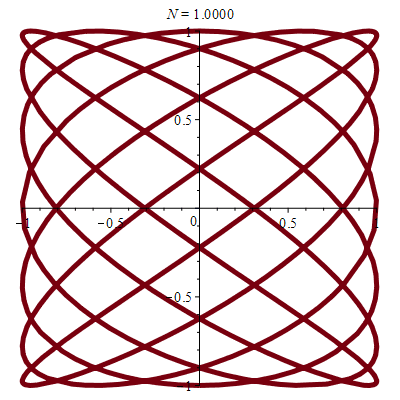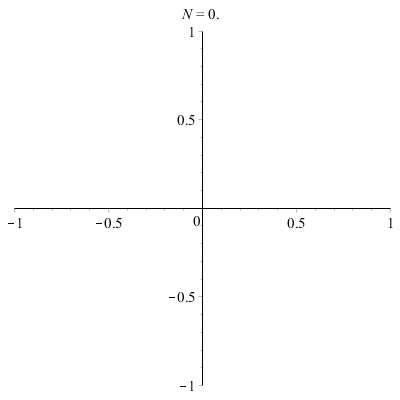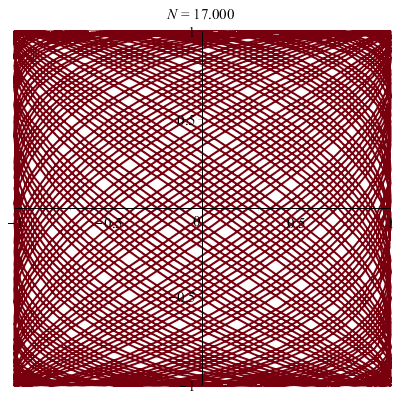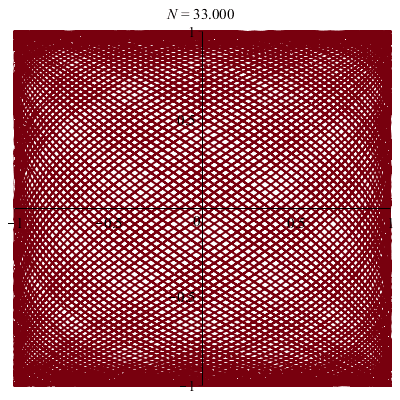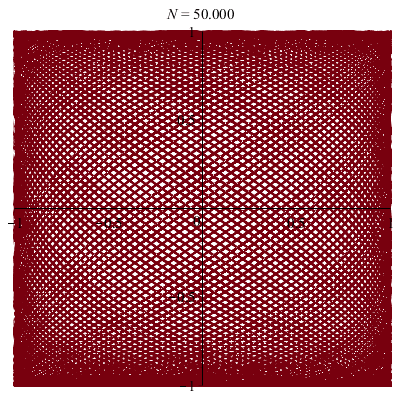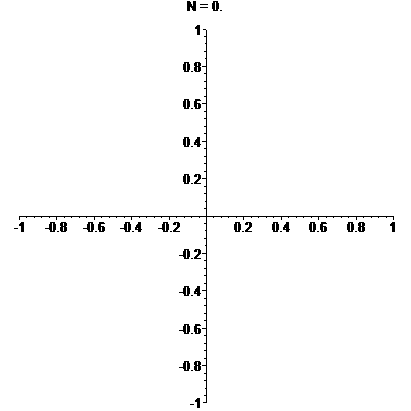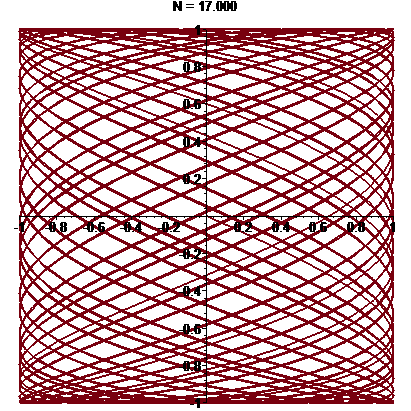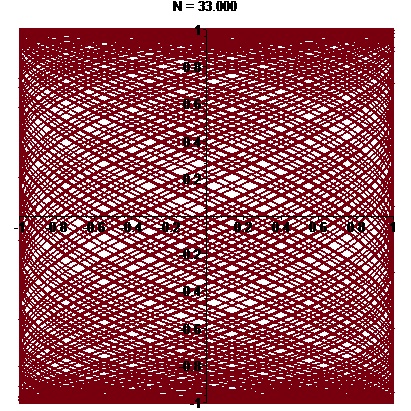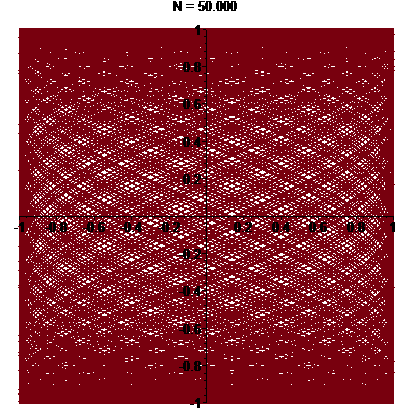| \(x(t)\!=\!a.\sin(pt)\) |
| \(y(t)\!=\!b.\sin(qt+\varphi)\) |
|
 |
| Jules-Antoine Lissajous |
| (1822–1880) |
| Physicien français |
|
\(\vphantom{/_p}a\!=\!b\!=\!1\;\quad p\!=\!q\!=\!1\;\quad \varphi\!=\!0\)
\(x(t)\!=\!\sin(t)\quad y(t)\!=\!\sin(t)\)
donc \(\;y\!=\!x\)
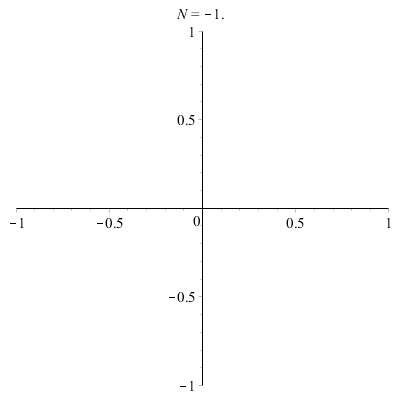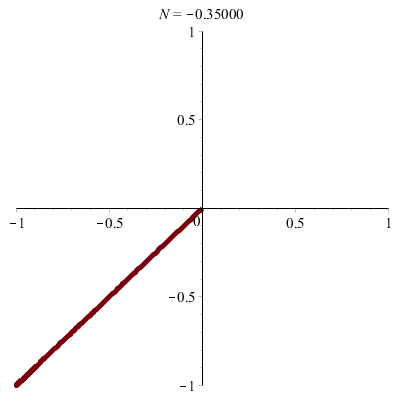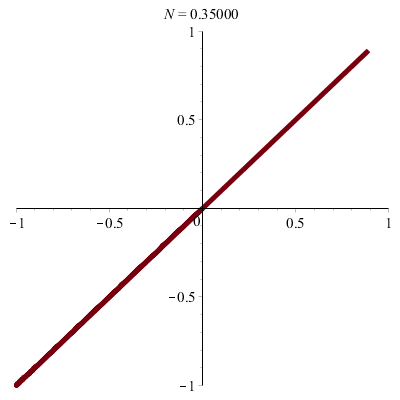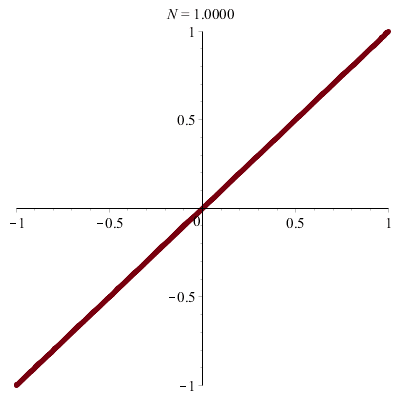

|
| |
| Segment ! |
\(\vphantom{/_p}a\!=\!b\!=\!1\;\quad p\!=\!q\!=\!1\;\quad\varphi\!=\!\pi/2\)
\(x(t)\!=\!\sin(t)\quad y(t)\!=\!\cos(t)\)
donc \(\;x^2+y^2\!=\!1\)
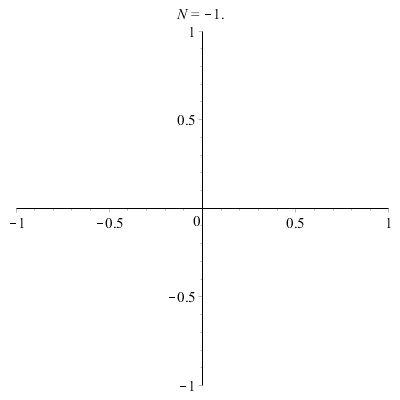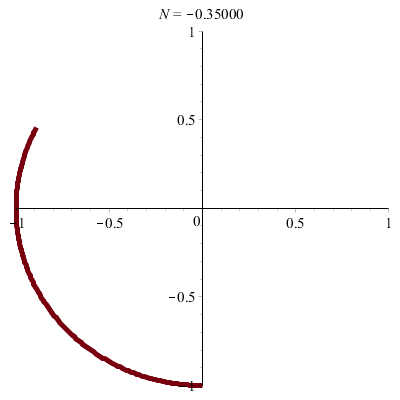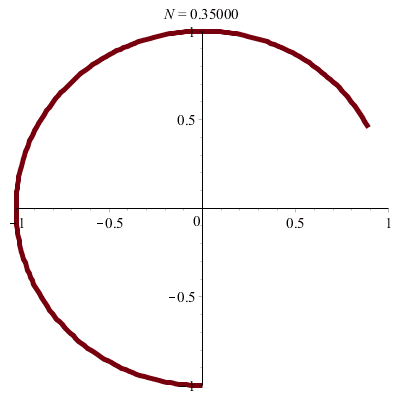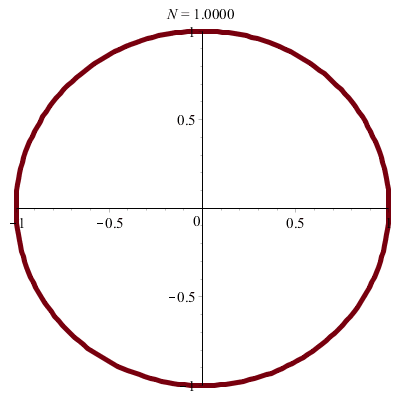
|
| |
| Cercle ! |
\(\vphantom{/_p}a\!=\!2, b\!=\!1\;\quad p\!=\!q\!=\!1\;\quad\varphi\!=\!\pi/2\)
\(x(t)\!=\! 2\sin(t)\quad y(t)\!=\!\cos(t)\)
donc \(\;\frac14x^2\!+\!y^2\!=\!1\)
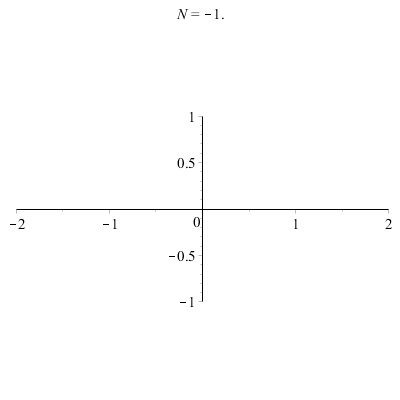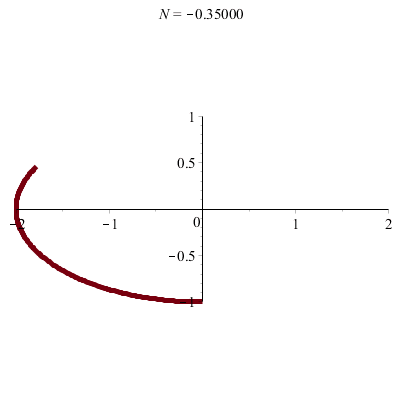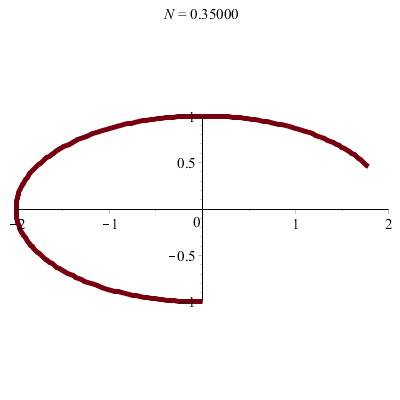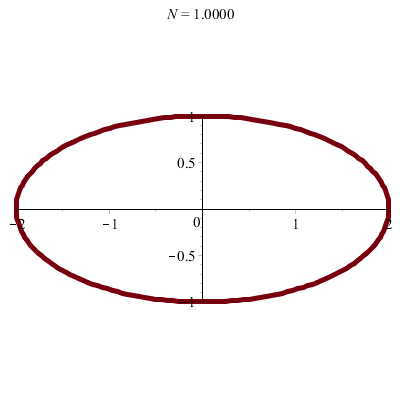
|
| |
| Ellipse ! |
\(\vphantom{/_p}a\!=\!3, b\!=\!2\;\quad p\!=\!q\!=\!1\;\quad \varphi\!=\!\pi/3\)
\(x(t)\!=\!3\sin(t)\quad y(t)\!=\!\sqrt3\cos(t)\!+\!\sin(t)\)
donc \(\;4x^2\!-6xy\!+9y^2\!=\!27\)
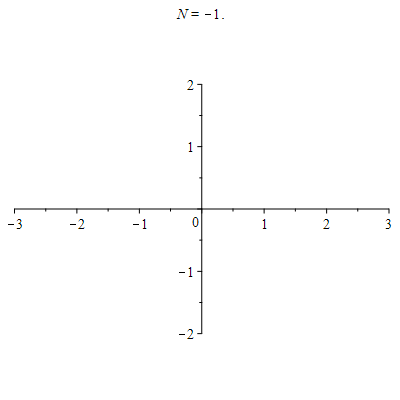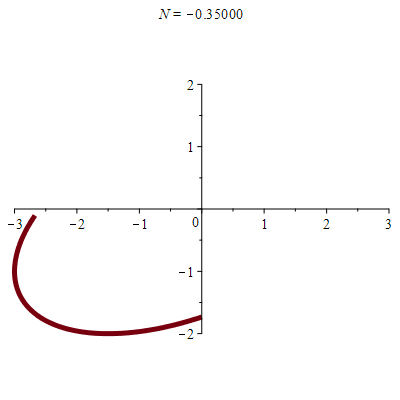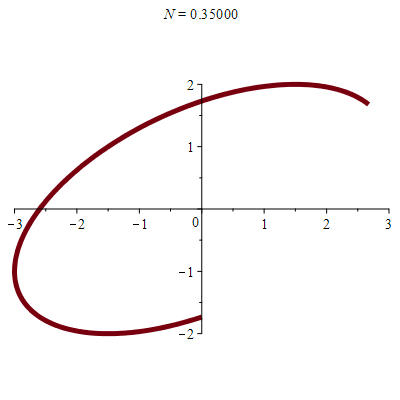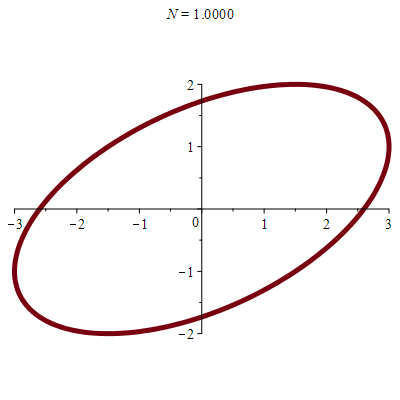

|
| |
| Une autre ellipse ! |
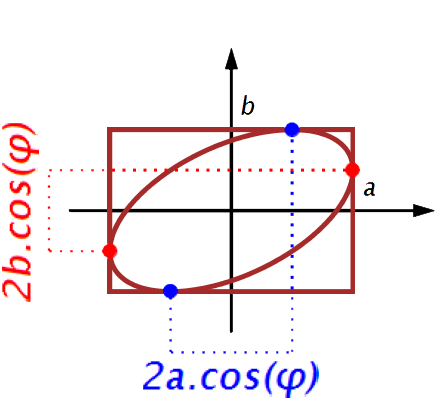
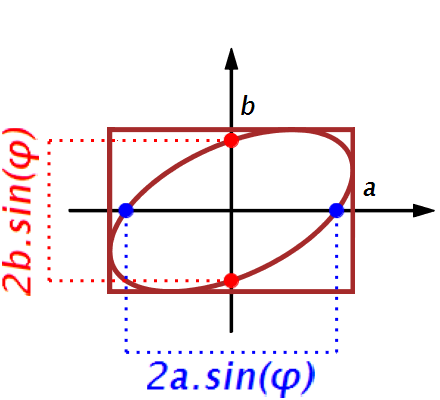
|
| |
| Détermination du déphasage |
Dorénavant, on choisira \(\;a\!=\!b\)
\(\vphantom{/_p}p\!=\!1,q\!=\!2\;\quad\varphi\!=\!0\)
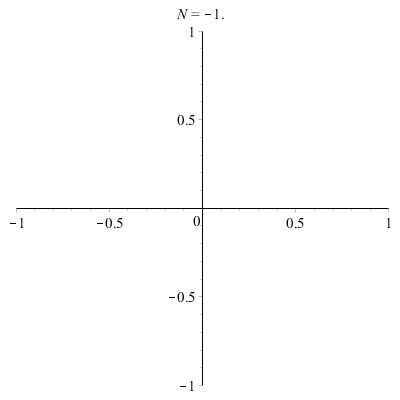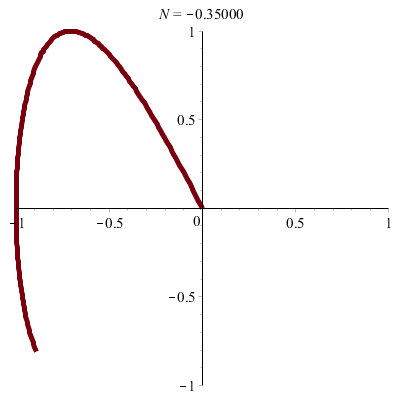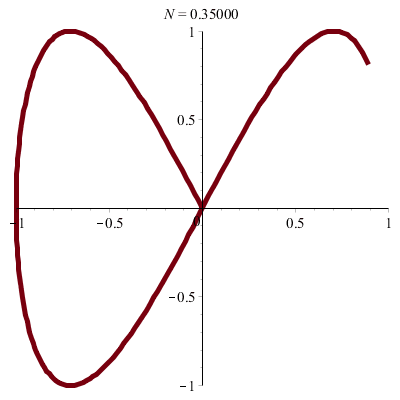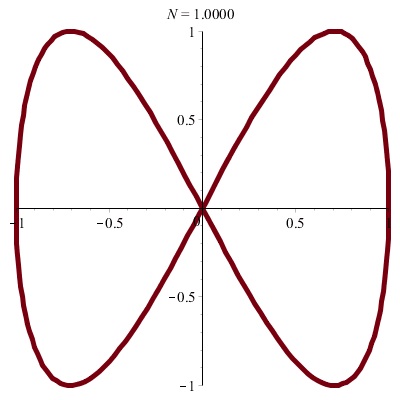
|
| |
| Lemniscate de Gerono… |
\(\vphantom{/_p}p\!=\!1, q\!=\!2\;\quad\varphi\!=–\pi/2\)
\(x(t)\!=\!\sin(t),\quad y(t)\!=–\cos(2t)\!=\!2\sin^2(t)–1\)
donc \(\;y\!=\!2x^2\!-\!1\)
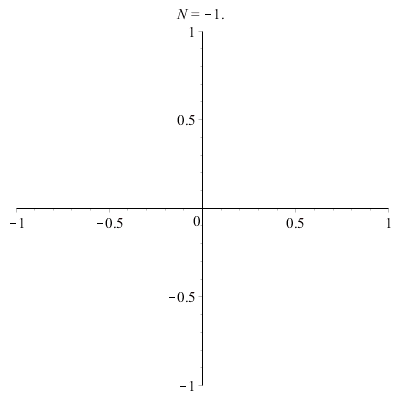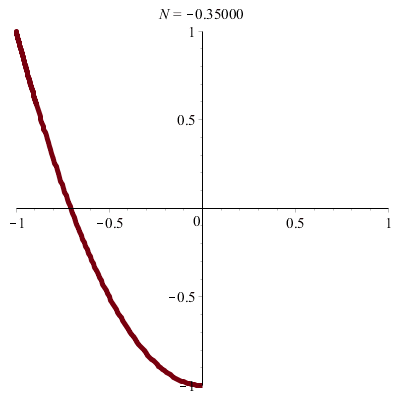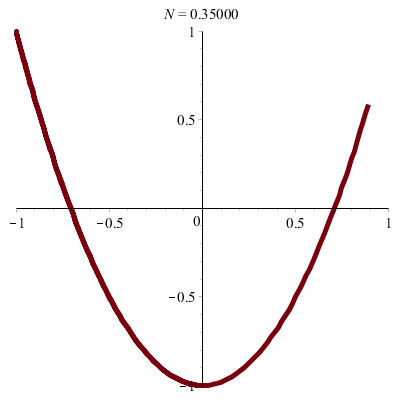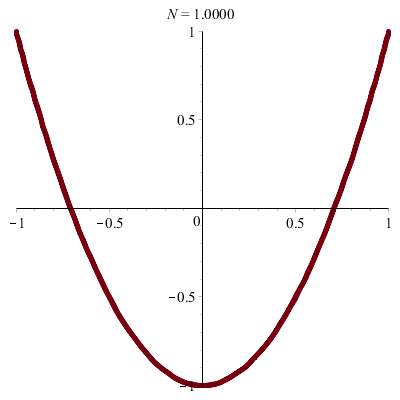
|
| |
| Parabole ! |
\(\vphantom{/_p}p\!=\!1, q\!=\!3\;\quad\varphi\!=\!0\)
\(x(t)\!=\!\sin(t),\quad y(t)\!=\!\sin(3t)\!=\!3\sin(t)–4\sin^3(t)\)
donc \(\;y\!=\!3x\,–4x^3\)
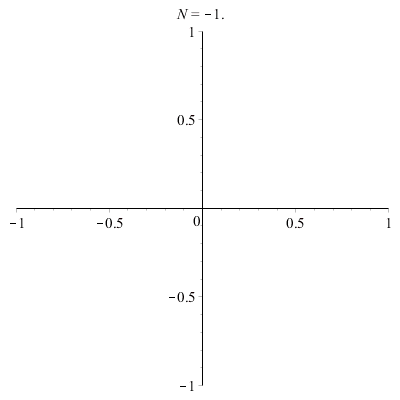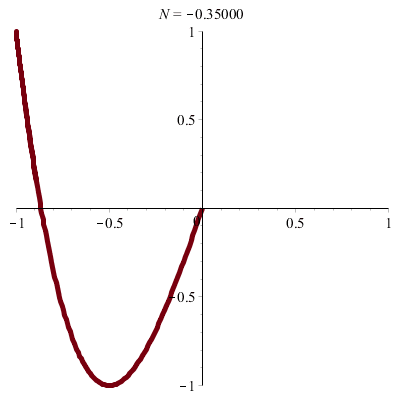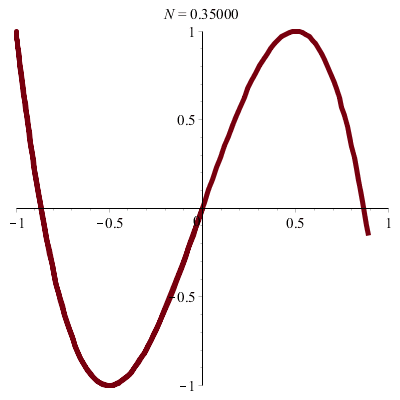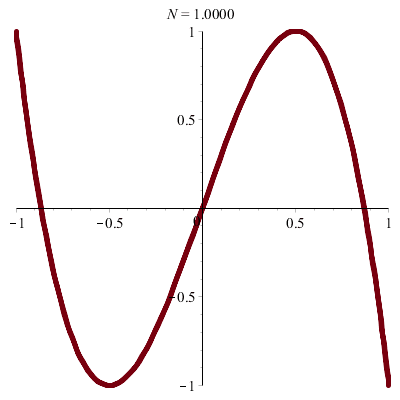
|
| |
| Cubique ! |
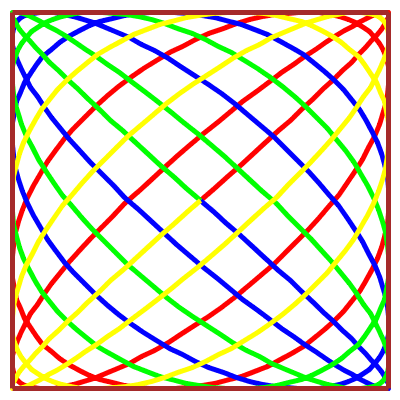
\(\vphantom{/_p}p\!=\!1, q\!=\!4\;\quad\varphi\!=\!0\)
\(\vphantom{/_p}p\!=\!1, q\!=\!6\;\quad\varphi\!=\!0\)
\(\vphantom{/_p}p\!=\!2, q\!=\!3\;\quad\varphi\!=\!0\)
\(\vphantom{/_p}p\!=\!2, q\!=\!5\;\quad\varphi\!=\!0\)
\(\vphantom{/_p}p\!=\!3, q\!=\!4\;\quad\varphi\!=\!0\)
\(\vphantom{/_p}p\!=\!3, q\!=\!4\;\quad\varphi\!=\!\pi/6\)
\(\vphantom{/_p}p\!=\!9, q\!=\!8\;\quad\varphi\!=\!0\)
\(\vphantom{/_p}p\!=\!7, q\!=\!5\;\quad\varphi\!=\!\pi/2\)
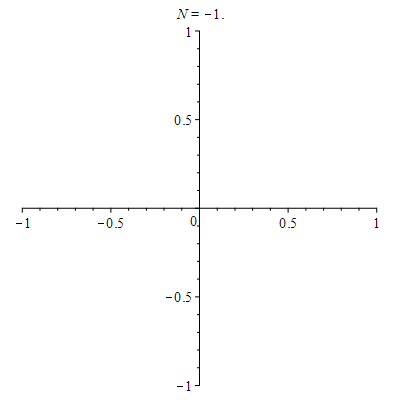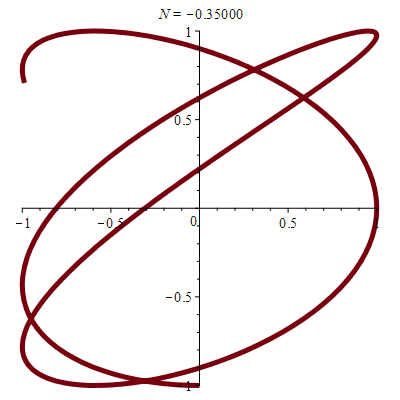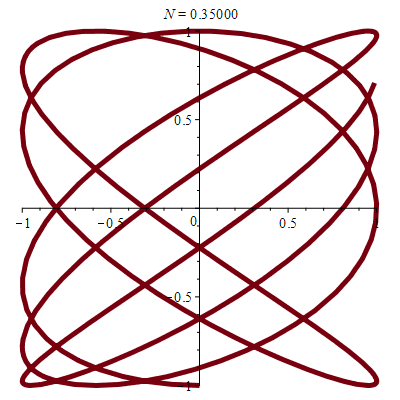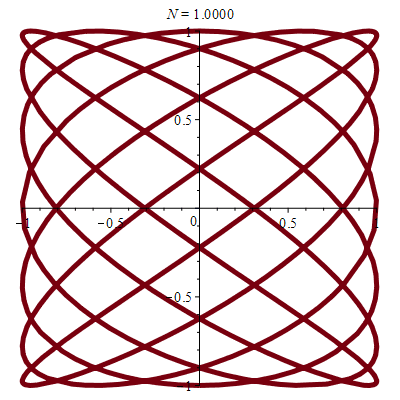
|
|

|
|
Un oscilloscope
|
|


|
|
Et un billard…
|
|
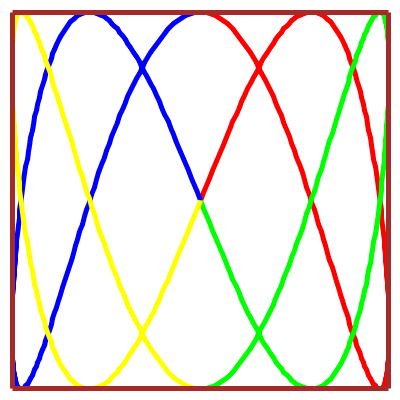
\(x(t)\!=\!a.\arcsin[\sin(pt)]\)
|
|
\(y(t)\!=\!b.\arcsin[\sin(qt+\varphi)]\)
|


|
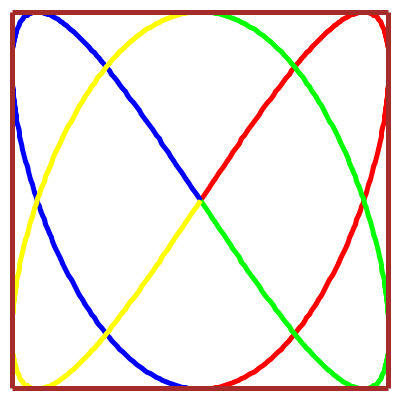
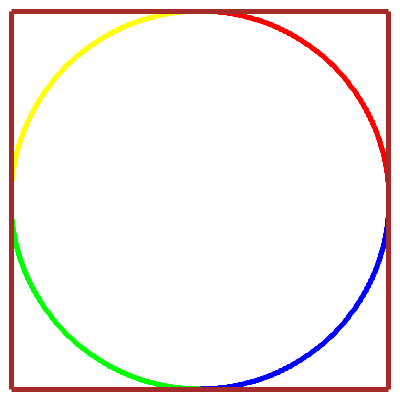
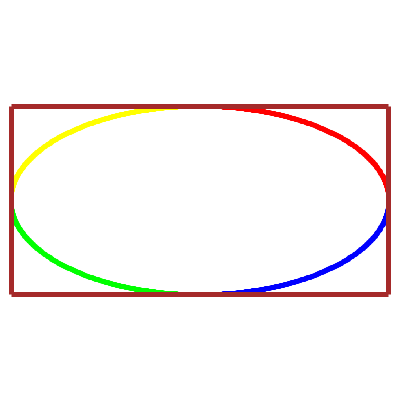
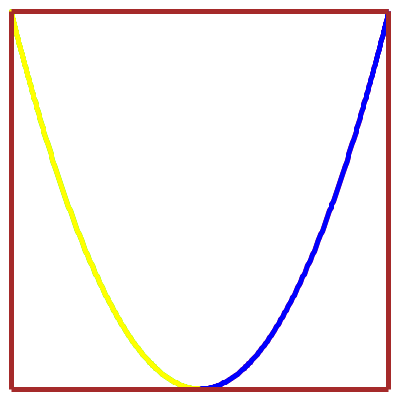
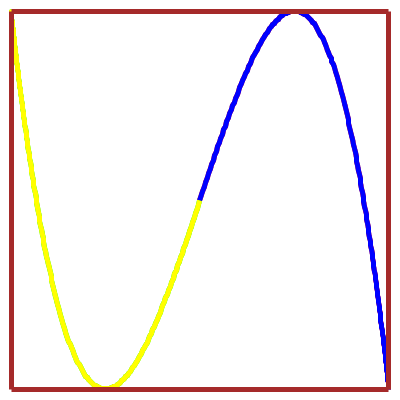
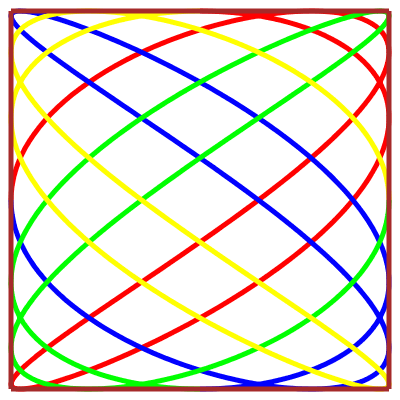
Billard rectangulaire
versus
courbe de Lissajous :
les trajectoires sont homéomorphes
(avec le même nombres de nœuds)…
|
\(\vphantom{/_p}p\!=\!7, q\!=\!5.1\;\quad\varphi\!=\!0\)
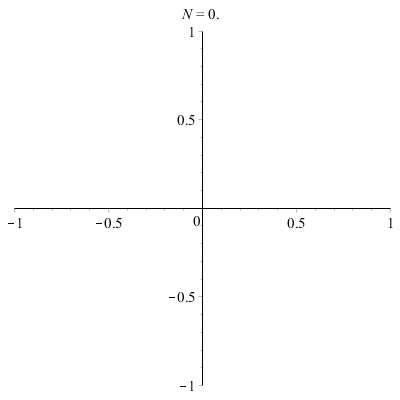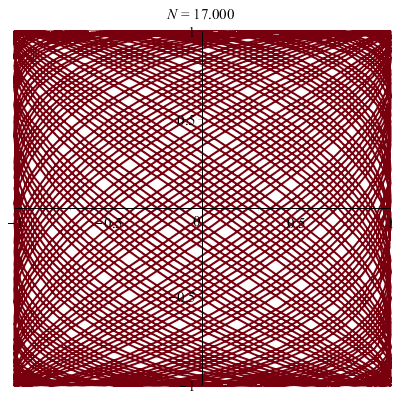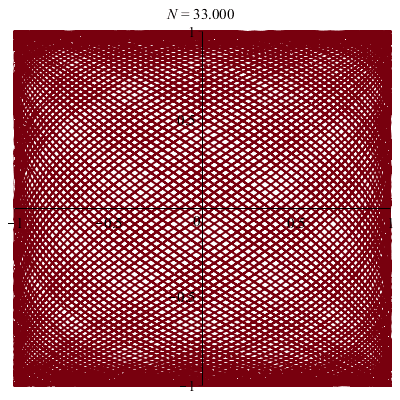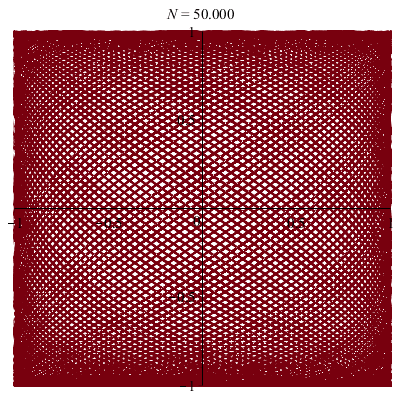

|
| |
| Une courbe fermée dans le carré… |
\(\vphantom{/_p}p\!=\!7, q\!=\!\pi\;\quad\varphi\!=\!0\)
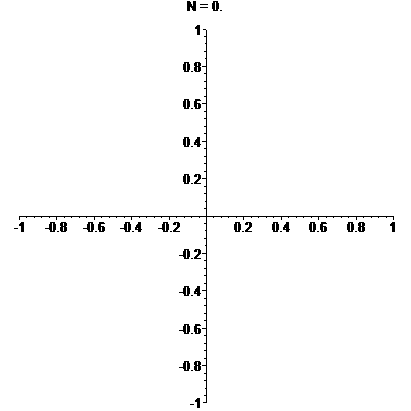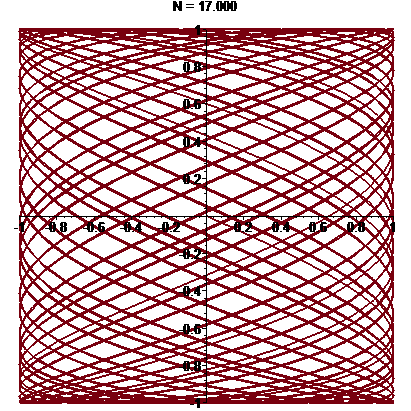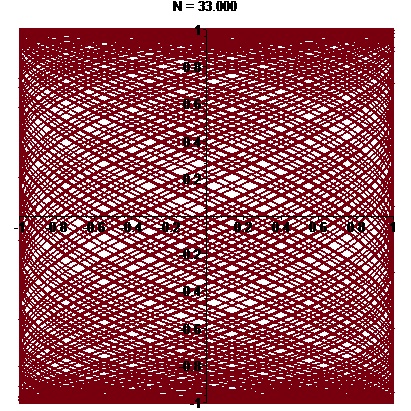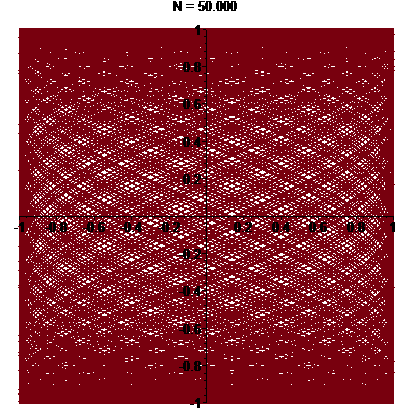

|
| |
| Une courbe dense dans le carré… |
|


|
| |
| et son billard correspondant… |
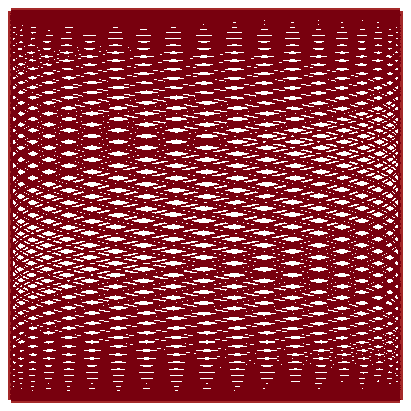
\(\vphantom{/_p}p\!=\!7, q\!=\!\sqrt2\;\quad\varphi\!=\!0\)

|
| |
| Une autre courbe dense dans le carré… |
La trajectoire est fermée
si et seulement si
les rapports des pentes
\(b/a\) (diagonale du rectangle) et \(bq/ap\) (trajectoire)
sont commensurables
i.e. \(p/q\in\mathbb{Q}\)
|
Quelques sites internet