\(\color{blue}\vphantom{()_p^q}f_n(x)\!=\!x^n\)

animation

Limite des \(\color{blue}f_n\) lorsque \(n\) tend vers l'infini :
0 partout sur [0,1] sauf en 1, et 1 en 1

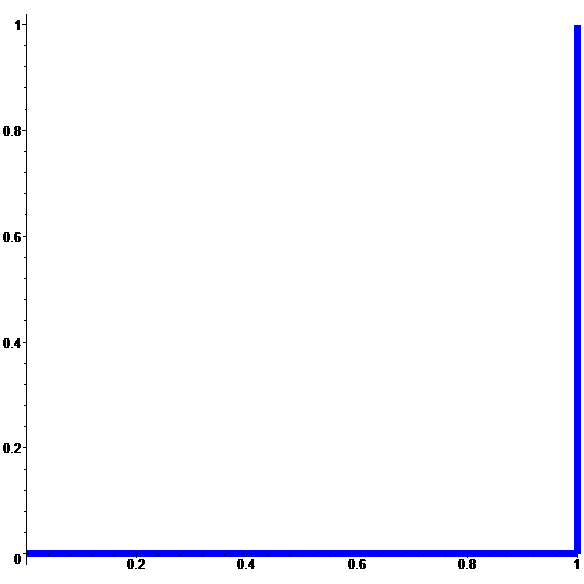
Graphe de \(\displaystyle\lim_{n\to\infty} \color{blue}f_n\)


Limite discontinue
d'une suite de fonctions continues…

\(\color{red}\vphantom{()_p^q}g_n(x)\!=\!x^n\!+\!(1–x)^n\!+\![4x(1–x)]^n\)

animation

Limite des \(\color{red}g_n\) lorsque \(n\) tend vers l'infini :
0 partout sur [0,1] sauf en 0,\(\mathbf{\frac12}\),1
et 1 en 0,\(\mathbf{\frac12}\),1

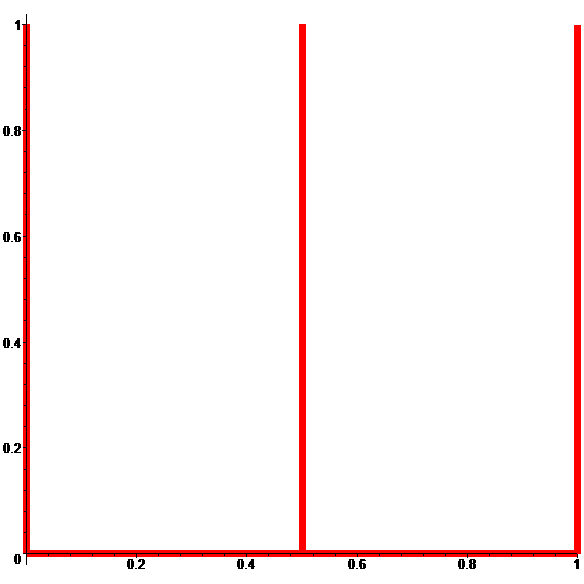
Graphe de \(\displaystyle\lim_{n\to\infty} \color{red}g_n\)


Limite discontinue
d'une suite de fonctions continues…