I. Définition et paramétrisation générale




Étymologie

κύκλος (« cercle »), τροχός (« roue ») et radical -είδος (« en forme de, semblable à »)


Définition (Pascal, 1623–1662)

La ROULETTE est une ligne si commune, qu'après la droite et la circonférence, il n'y en a point de si fréquente ; et elle se décrit si souvent aux yeux de tout le monde qu'il y a lieu de s'étonner qu'elle n'ait pas été considérée par les anciens, dans lesquels on n'en trouve rien.

Car ce n'est autre chose que le chemin que fait en l'air le clou d'une roue, quand elle roule de son mouvement ordinaire, depuis que le clou commence à s'élever de terre, jusqu'à ce que le roulement continu de la roue l'ait rapporté à terre, après un tour entier achevé : supposant que la roue soit un cercle parfait, le clou un point dans sa circonférence, et la terre parfaitement plane.


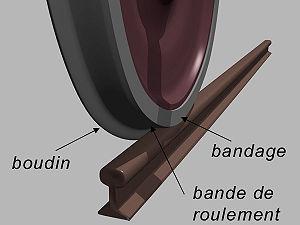
Origines


Quelques sites internet



Paramétrisation


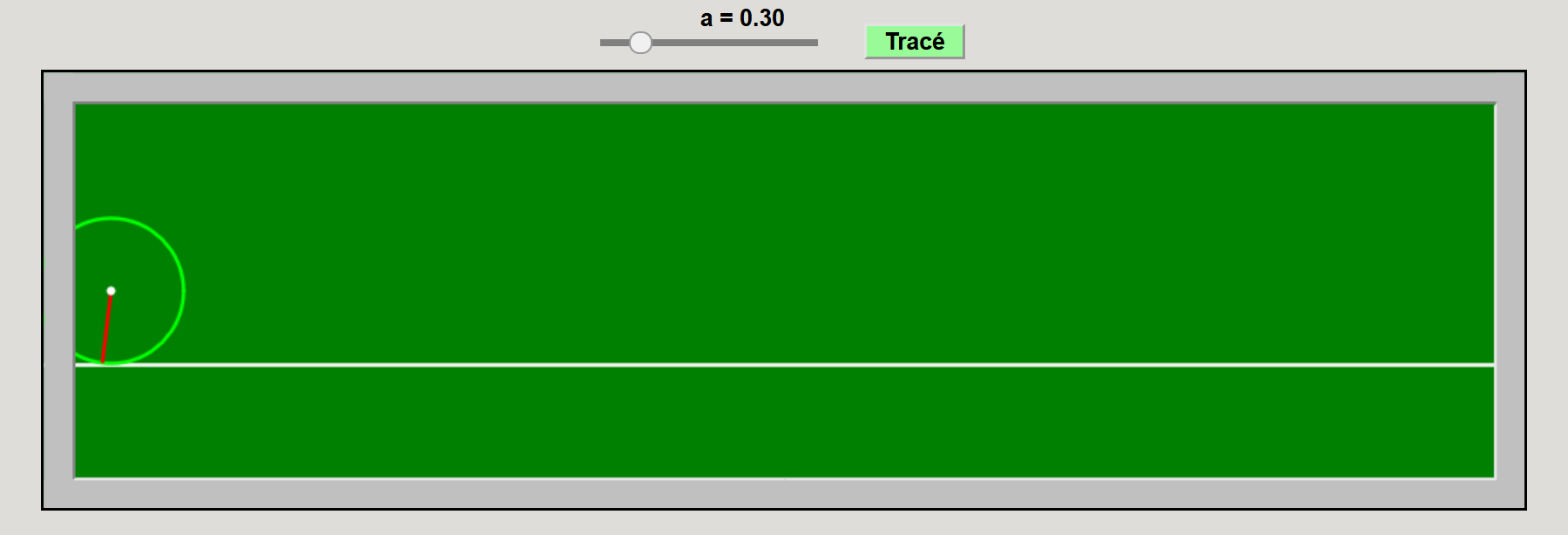
Cycloïde/trochoïde
(cercle de rayon \(r\) roulant sur une droite,
trajectoire d'un point situé à une distance \(a\) du centre du cercle mobile)

\(x_0(t)=rt-a\sin(t)\)
\(y_0(t)=r-a\cos(t)\)

ou encore

\(z_0(t)=r(t+i)-a\,\mathrm{e}^{\mathrm{i}(\frac{\pi}{2}-t)}\)




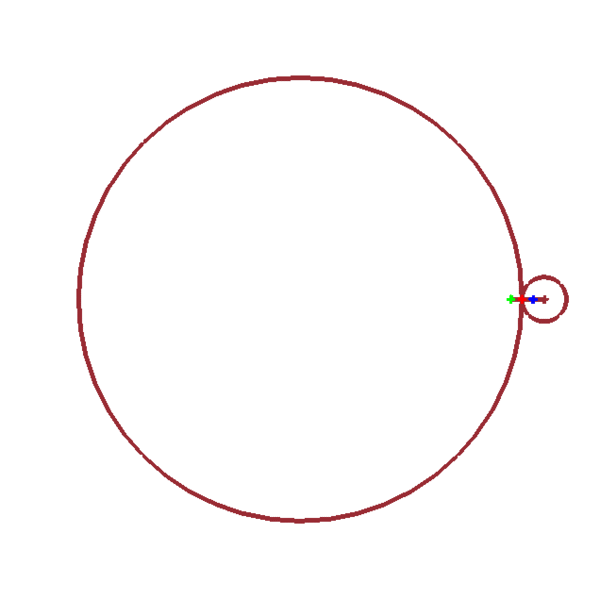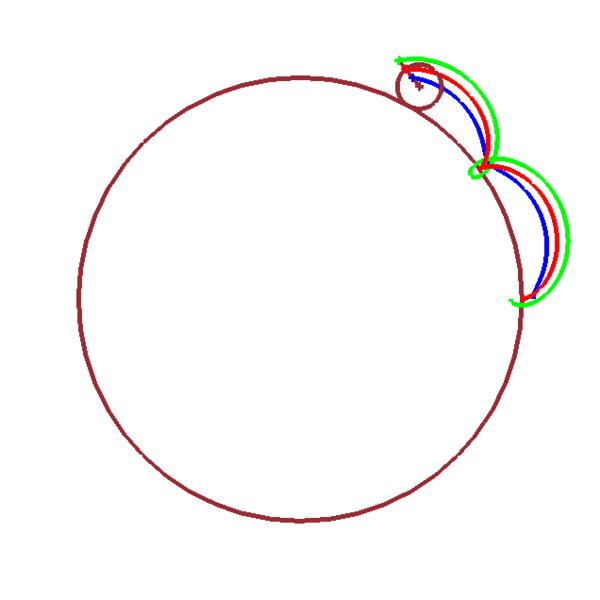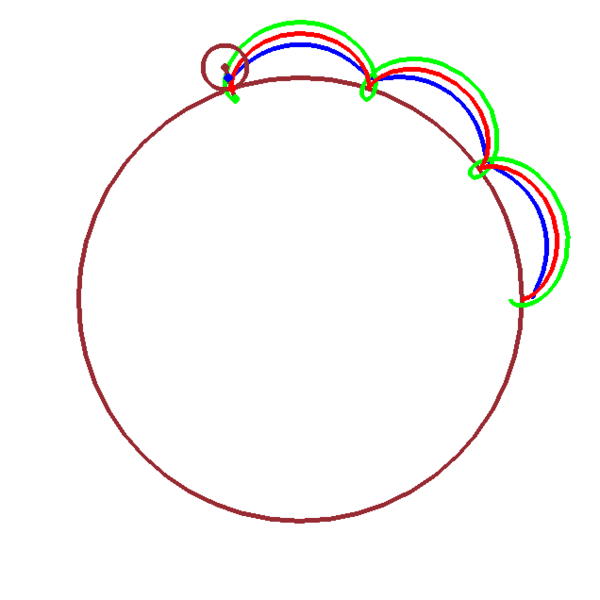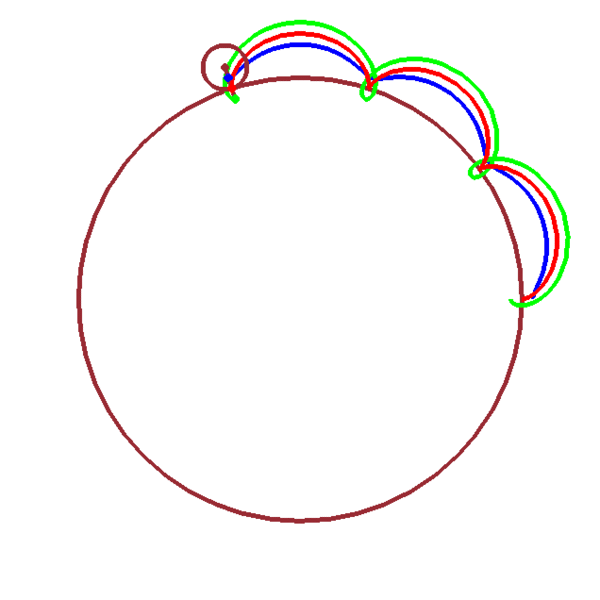
Épicycloïde/épitrochoïde
(cercle de rayon \(r\) roulant sur un cercle de rayon \(R\))

\(x_1(t)=(n+1)r\cos(t)+a\cos[(n+1)t]\)
\(y_1(t)=(n+1)r\sin(t)+a\sin[(n+1)t]\)

ou encore

\(z_1(t)=(n+1)r\,\mathrm{e}^{\mathrm{i}t}+a\,\mathrm{e}^{\mathrm{i}(n+1)t}\)

avec \(n=\dfrac{\raise -1ex R}{\raise 1ex r}\)




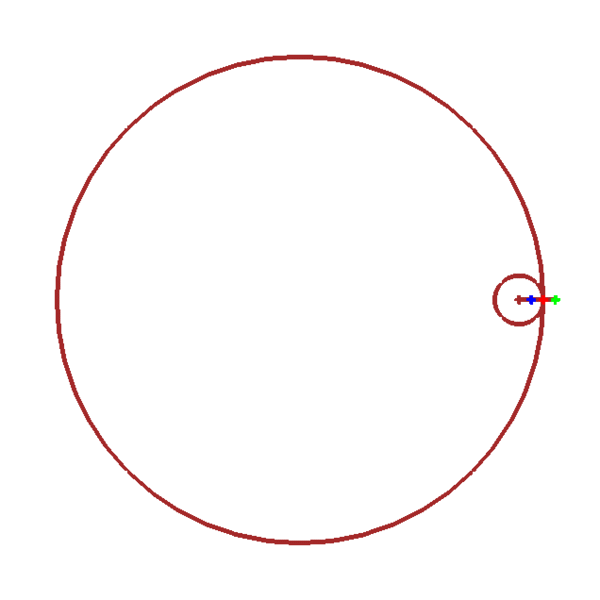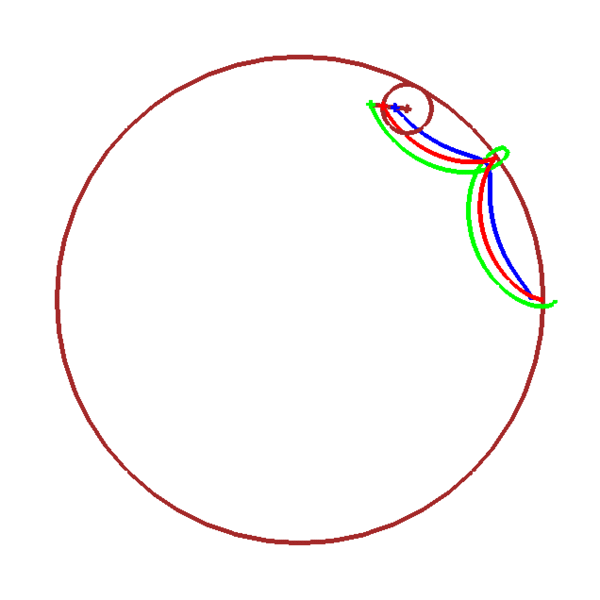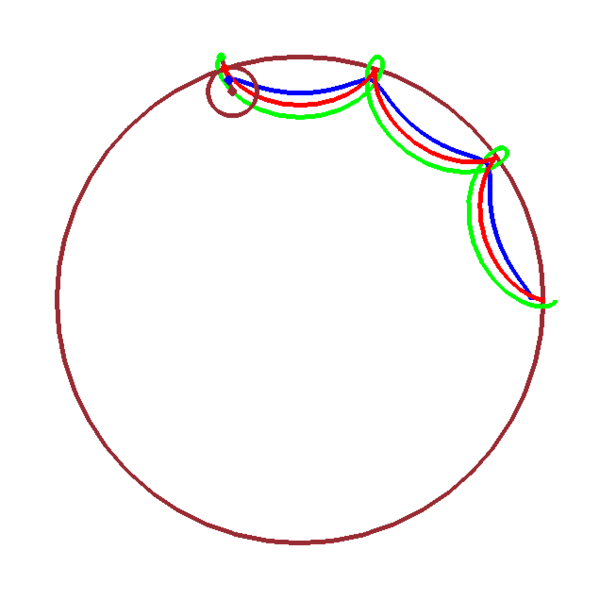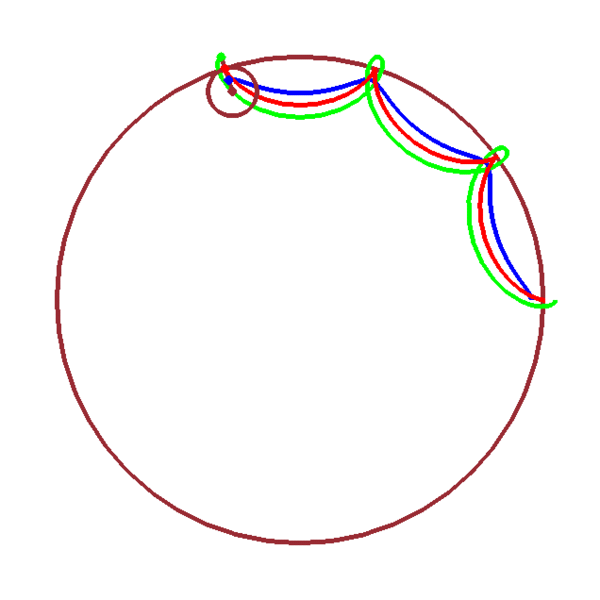
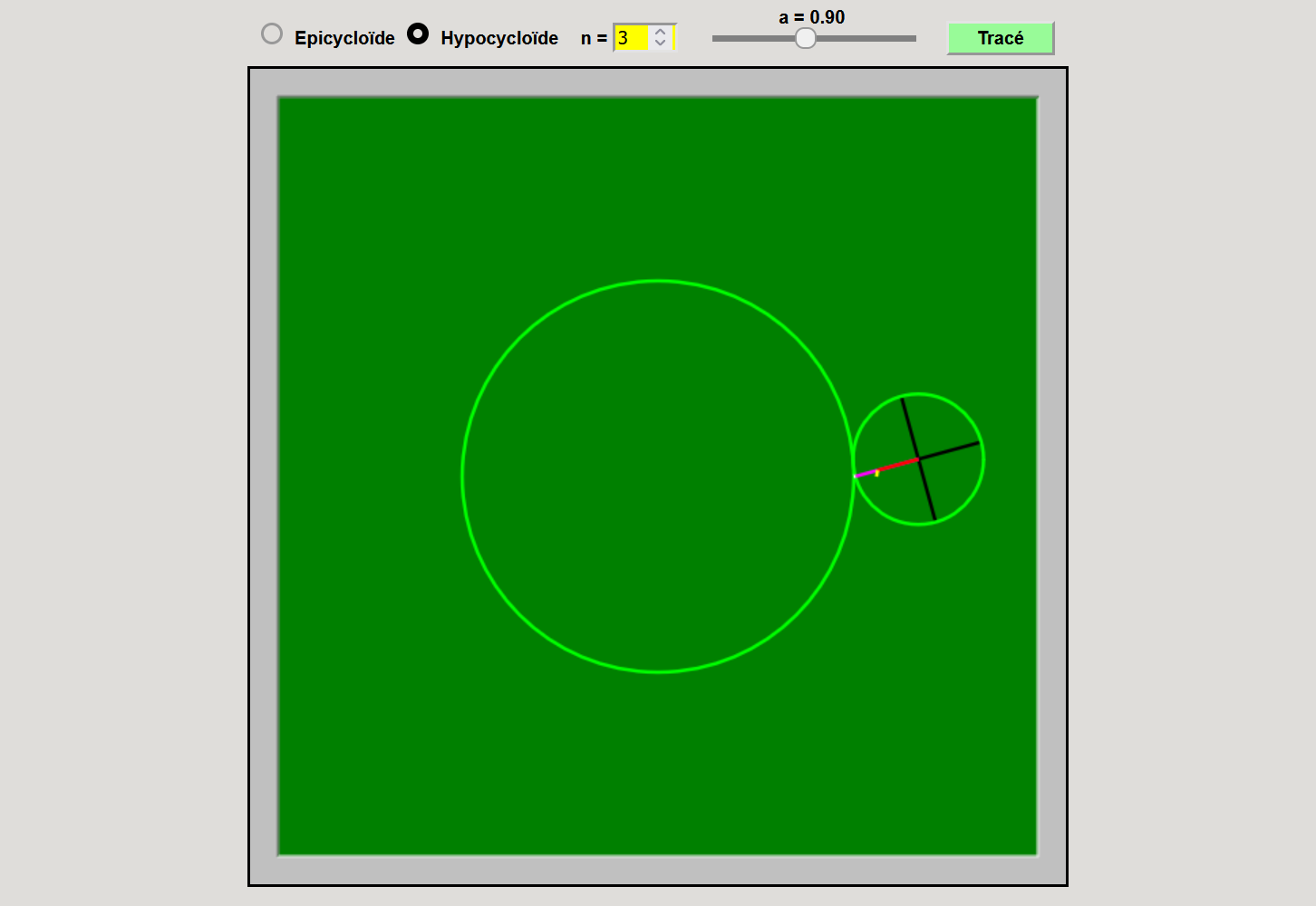
Hypocycloïde/hypotrochoïde
(cercle de rayon \(r\) roulant dans un cercle de rayon \(R\))

\(x_2(t)=(n-1)r\cos(t)-a\cos[(n-1)t]\)
\(y_2(t)=(n-1)r\sin(t)+a\sin[(n-1)t]\)

ou encore

\(z_2(t)=(n-1)r\,\mathrm{e}^{\mathrm{i}t}-a\,\mathrm{e}^{-\mathrm{i}(n-1)t}\)

avec \(n=\dfrac{\raise -1ex R}{\raise 1ex r}\)





NB : dans toute la suite on choisira \(r=1\) (donc \(n=R\))




   
◄ Sommaire ►