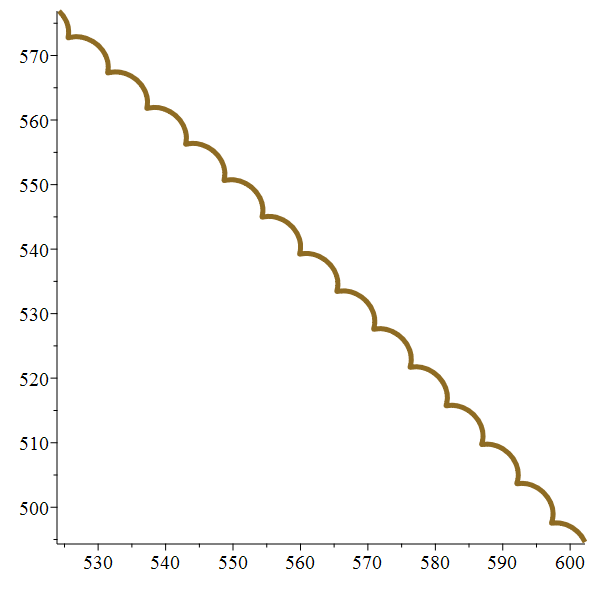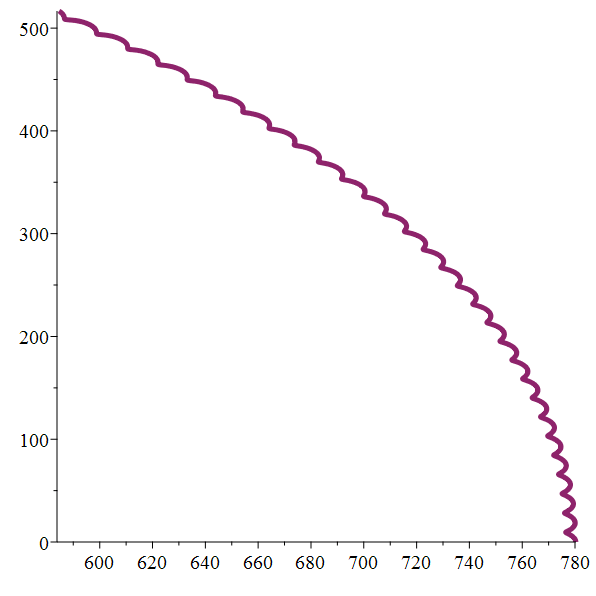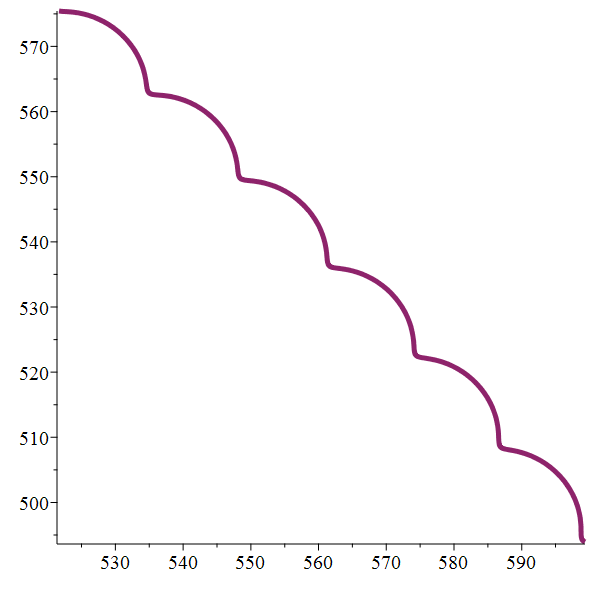| V. Et dans la vie de tous les jours… |
Un peu d'optimisation : des pendules,
\(\vphantom{a_a}\)des toboggans et des tunnels
Entre deux cycloïdes superposées :
un fil pesant suspendu à une pointe…
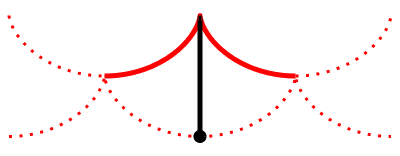
Un pendule cycloïdal…
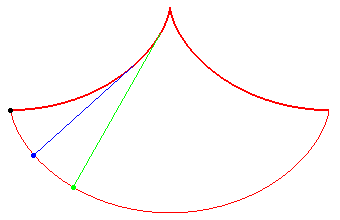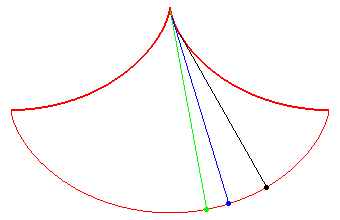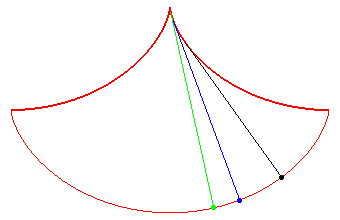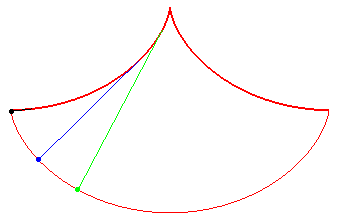
La cycloïde, une courbe isochrone
Quelle que soit leur position de départ,
les billes ont la même période !

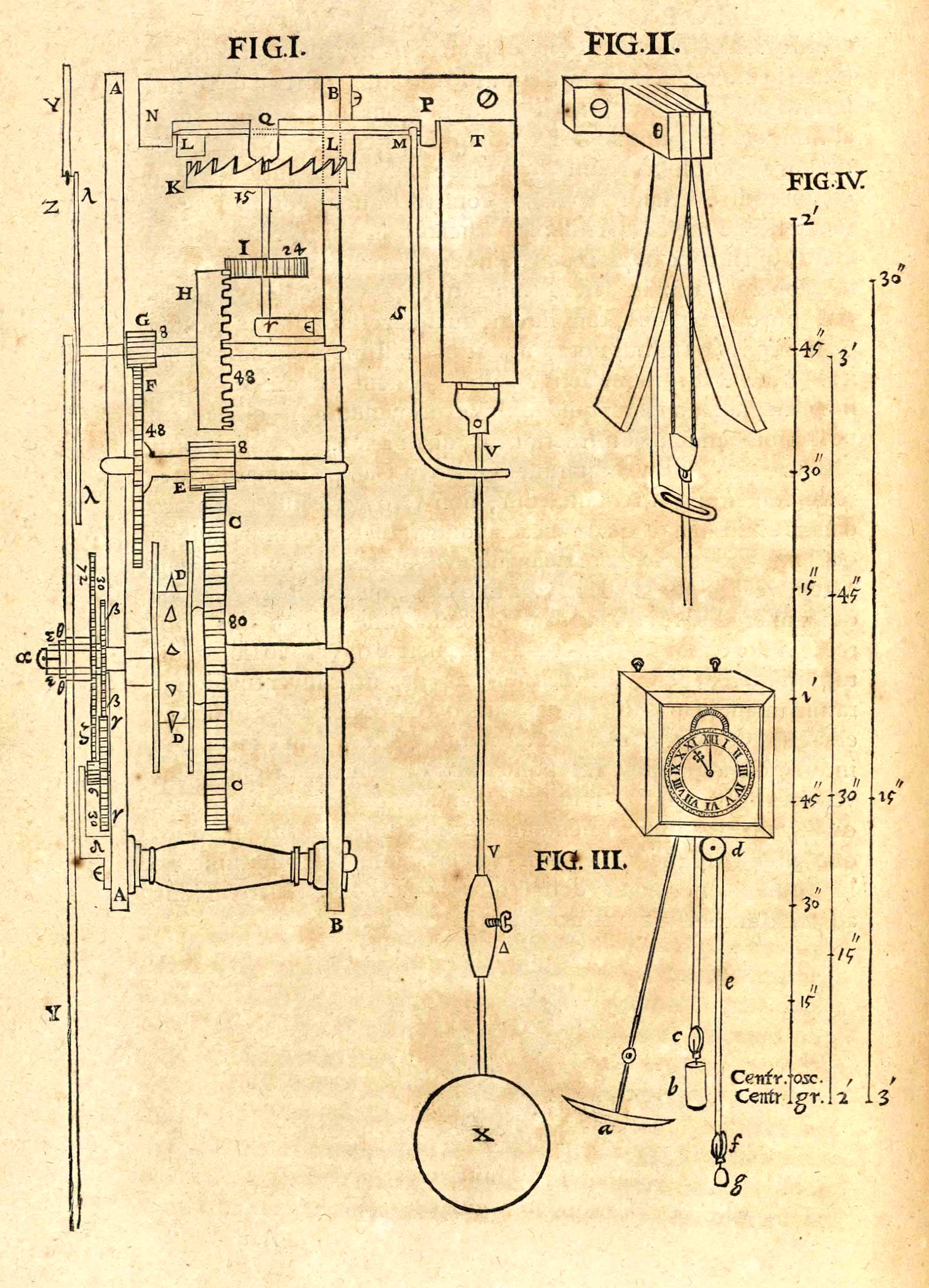
Pendule de Huygens (1656) :
horloge à balancier cycloïdal
 |
| Christiaan Huygens |
| (1629–1695) |
Mathématicien, astronome
et physicien néerlandais |
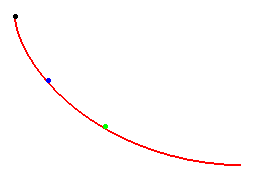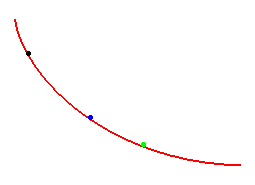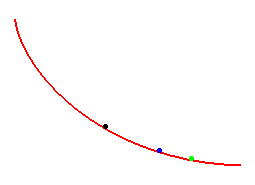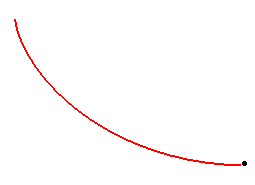

La cycloïde, une courbe tautochrone
Quelle que soit leur position de départ,
les billes arrivent au pied de la courbe au même instant !
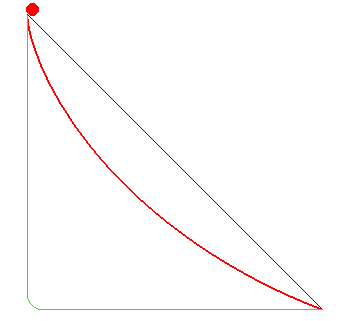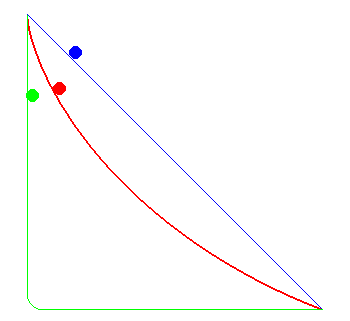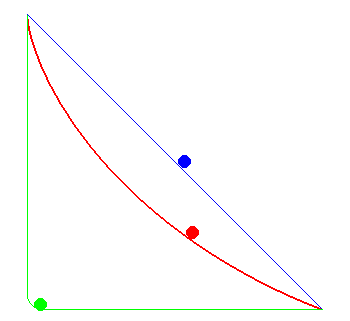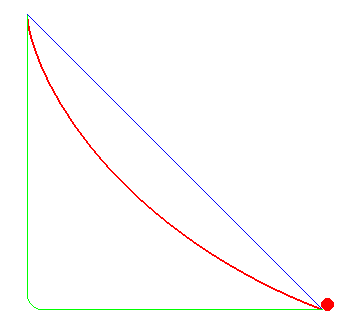
La cycloïde, une courbe brachistochrone
Parmi toutes les courbes joignant deux points fixés,
la cycloïde offre un temps de parcours minimal !
Le chemin le plus court n'est pas le plus rapide…
–––––––––
Une utopie onirique : les tunnels gravitationnels
(XVIIe s. puis années 60)
Sous l'effet de la gravitation terrestre…

animation 
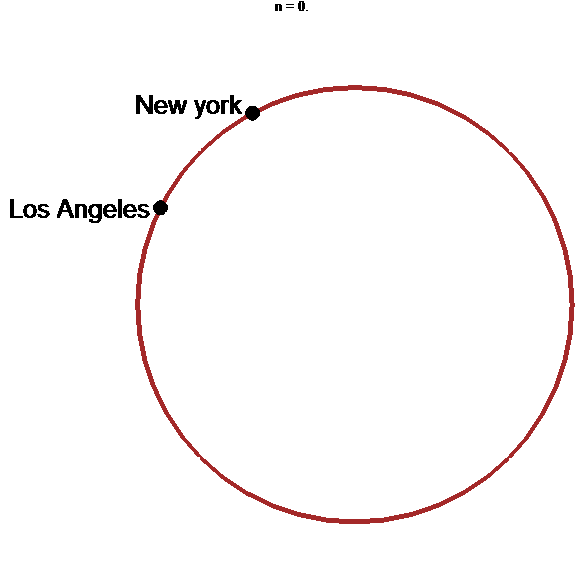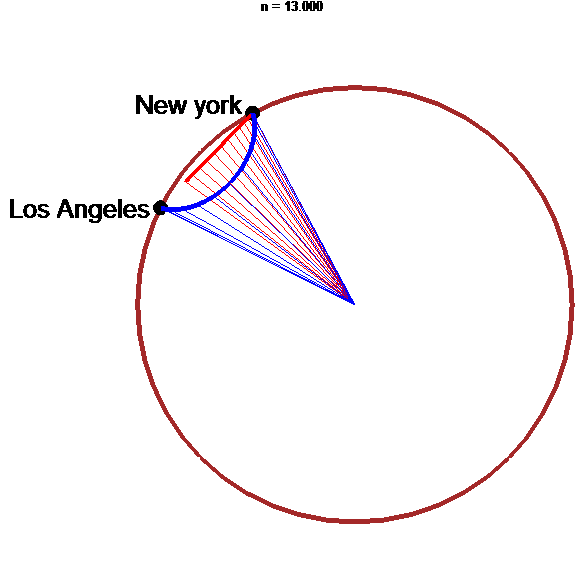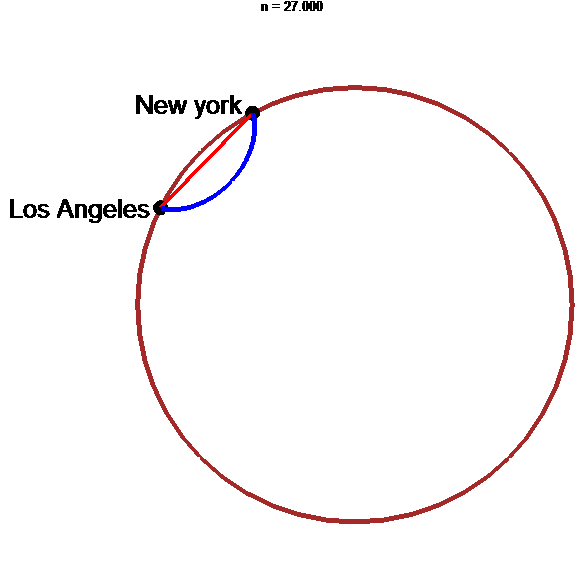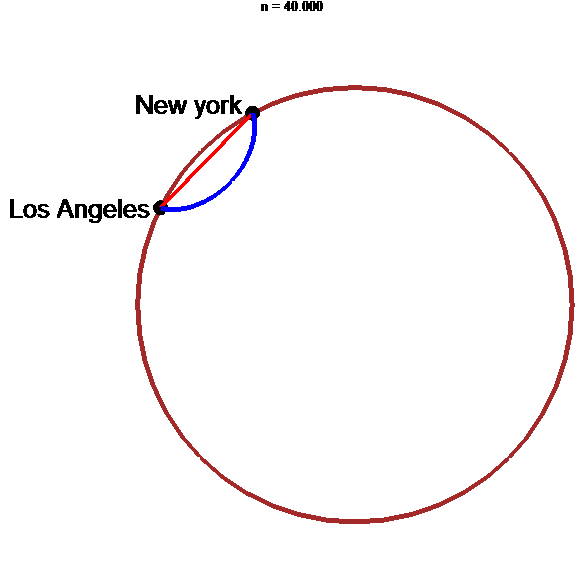
stop 

Tunnel le plus rapide : arche d'hypocycloïde !!!

animation 
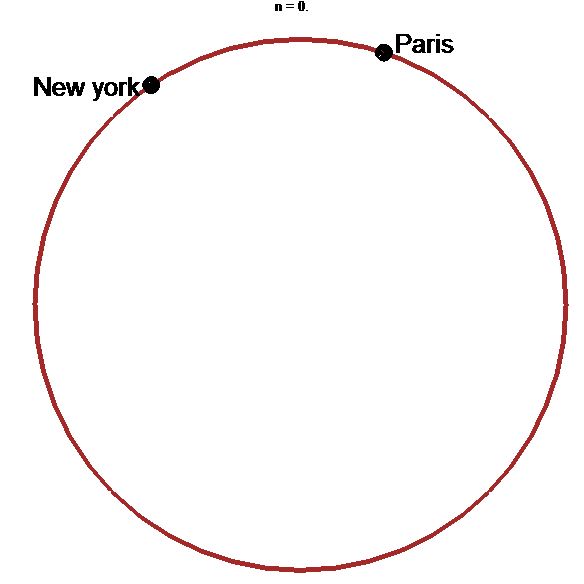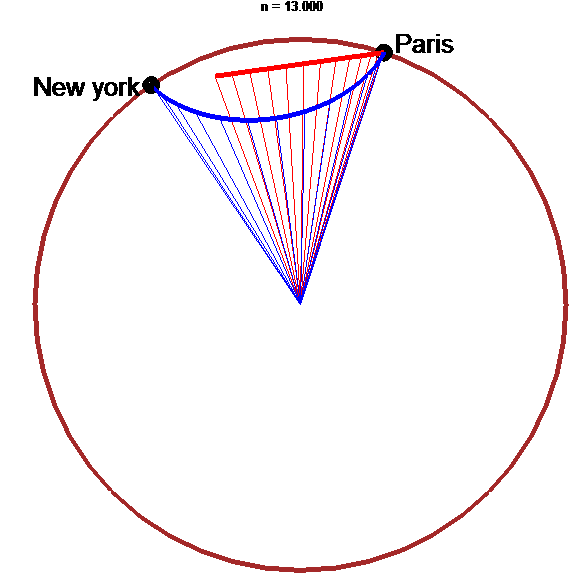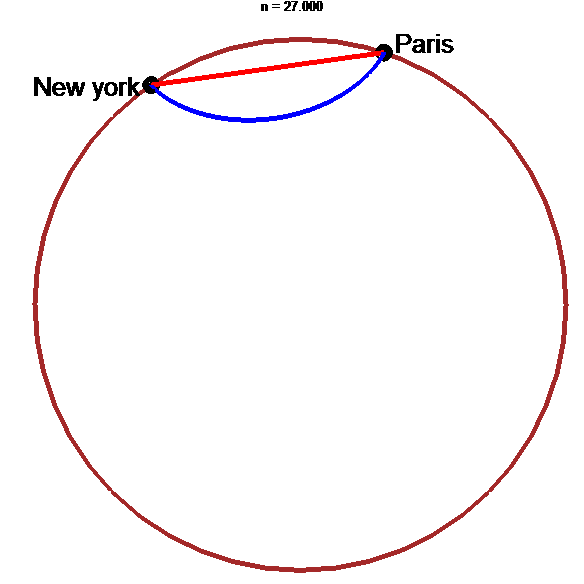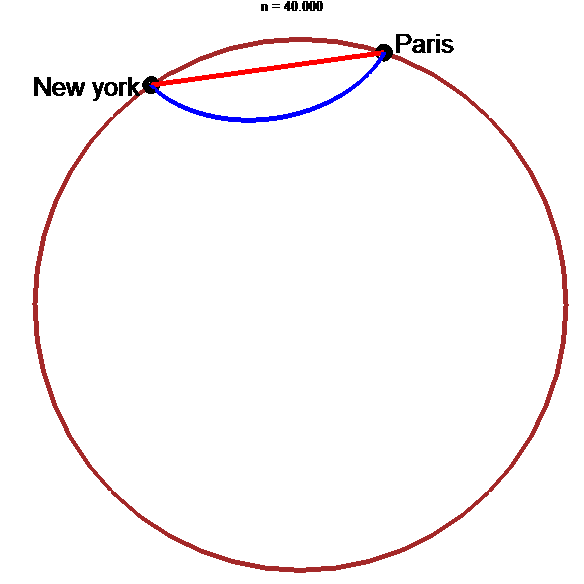
stop 
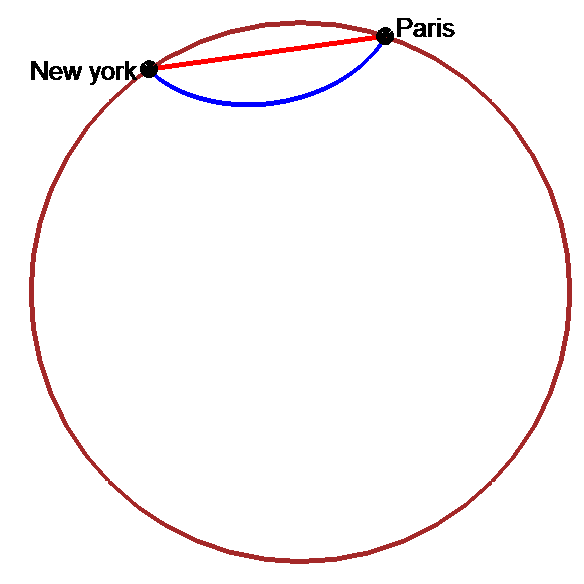
Tunnel le plus rapide : arche d'hypocycloïde !!!
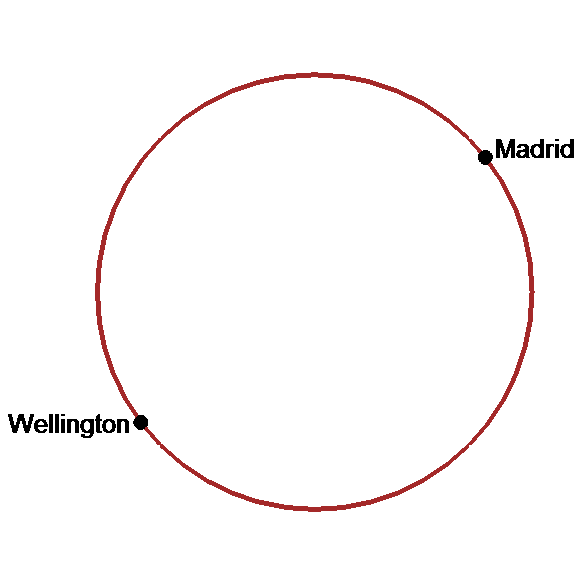
animation 
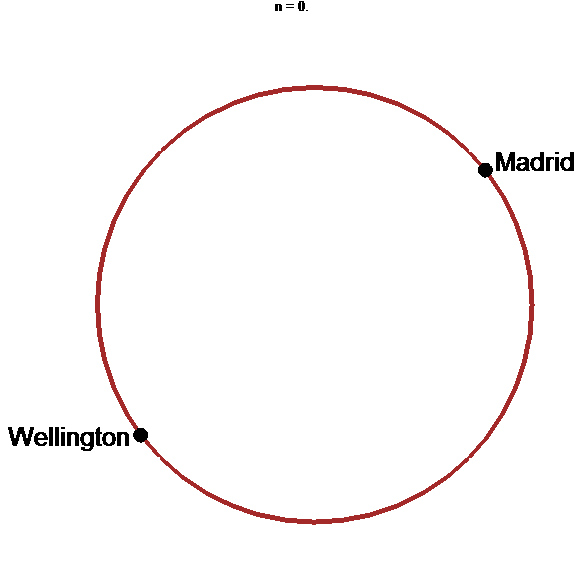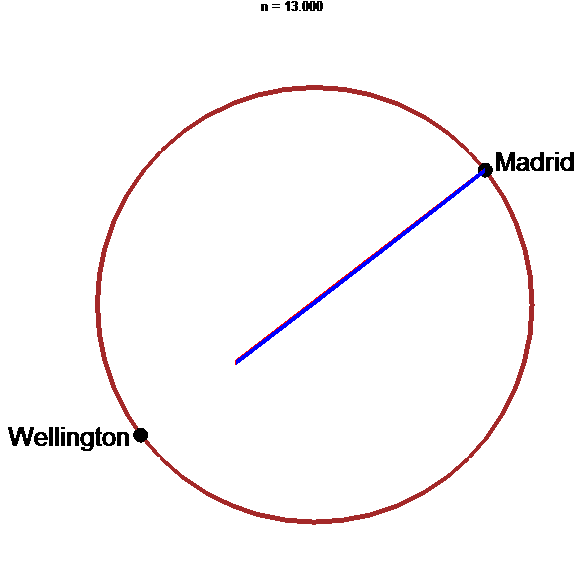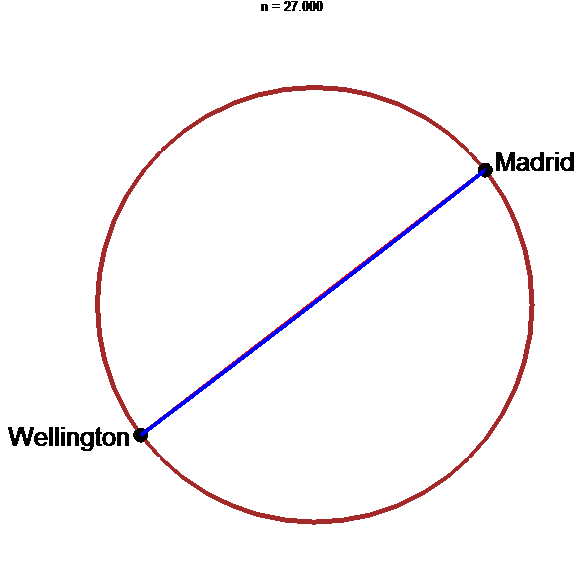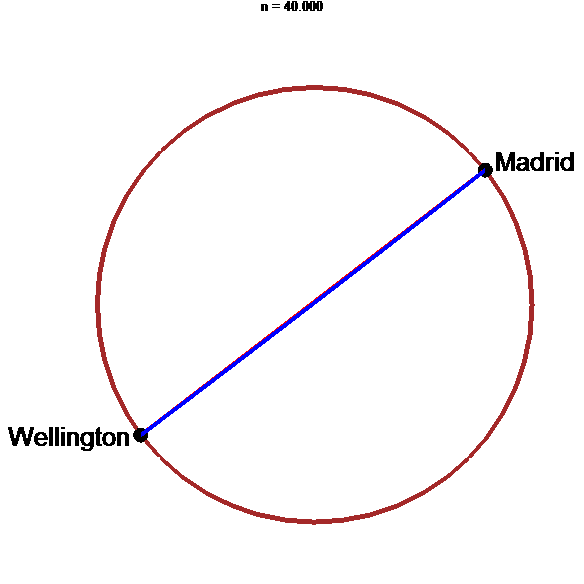
stop 
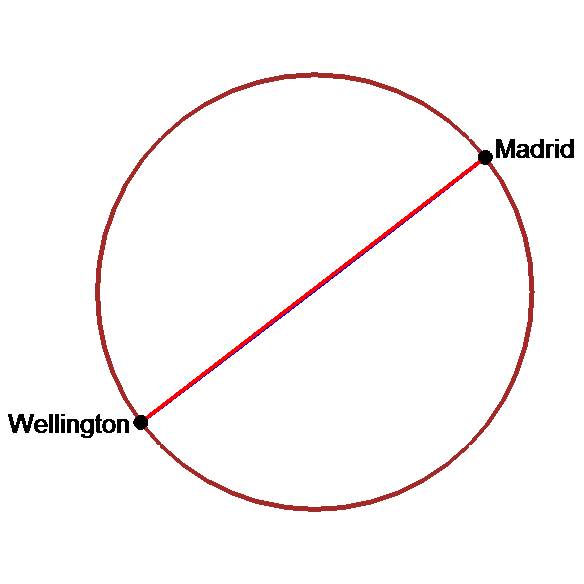
Tunnel le plus rapide : le diamètre du globe !!!
Quelques équations…
Segment reliant \(A\) et \(B\) :
\(z = z_A + u(z_B-z_A),\quad u \!\in\! [0,1]\)
Hypocycloïde reliant \(A\) et \(B\) :
\(z = (R-r_{\!\raise-0.5ex{AB}}) \,\mathrm{e}^{\mathrm{i}(u + \theta_A)}
\,+\, r_{\!\raise-0.5ex{AB}} \,\mathrm{e}^{-\mathrm{i}(R/r_{\!\raise-0.5ex{AB}}-1)u + \mathrm{i}\theta_A},
\quad u \!\in\![0,\theta_{AB}]\)
\(r_{\!\raise-0.5ex{AB}} = R \dfrac{\theta_{\!AB}}{2\pi}\),\(\quad\theta_{\!AB} = \theta_B-\theta_A\)
Loi horaire :
\(u(t) = \frac12 \left[1-\cos\left(\sqrt{\frac gR}\,t\right)\right],\quad t\!\in\!\big[0,2\pi\sqrt{R/g}\,\big]\)
pour le segment
\(u(t) = \sqrt{\frac gR\frac{\theta_{AB}}{2\pi-\theta_{AB}}}\,t,\quad
t\!\in\!\big[0,\sqrt{\theta_{AB}(2\pi-\theta_{AB}) (R/g)}\,\big]\)
pour l'hypocycloïde
Lois de la physique :
Force de gravitation : \(F(r) = \dfrac{GM(r)m}{r^2} = \dfrac{mgr}{R}\)
avec \(M(r) = M \dfrac{\raise -0.5ex {r^3}}{R^3}\vphantom{\dfrac{b^b}{p}}\)
\(M =\) masse de la terre, \(M(r)=\) masse de la partie de rayon \(r\)
\(R = 6371 \,\mathsf{km}\;\) rayon de la terre
\(G=\) constante de gravitation
\(g = \dfrac{GM}{R^2} = 9.81 \,\mathsf{m}/\mathsf{s}^2\) : accélération de la pesanteur
Conservation de l'énergie :
\(\dfrac12 mv^2 + \dfrac{1}{2R}mgr^2 = \dfrac12 mgR\)
ou encore
\(v = \sqrt{\frac gr (R^2-r^2)}\)
Durée de la traversée :
\(T_{AB} = \sqrt{\theta_{AB}(2\pi-\theta_{AB}) \frac Rg}\)
Longueur du tunnel :
\(L_{AB} = \dfrac{2}{\pi^2}R\theta_{AB}(2\pi-\theta_{AB})\)
Profondeur du tunnel : \(P_{AB} = \dfrac{1}{\pi}R\theta_{AB}\)
Vitesse au milieu : \(V_{AB} = \dfrac{1}{\pi}\sqrt{gR\theta_{AB}(2\pi-\theta_{AB})}\)
Durée : 42,24 minutes !
Quelques petits inconvénients…
Profondeur : 6371 km
Vitesse au centre : 28440 km/h
Température au centre : 5430°C
Merci d'avoir rêvé avec nous !
\(\vphantom{a_q}\)Un peu d'électromagnétisme
Considérons dans un repère orthonormé \((O,\vec{i},\vec{j},\vec{k})\)
une particule de masse \(m\) et de charge \(q\)
située initialement à l'origine et animée d'une vitesse initiale \(\vec{v}_0\)
placée dans un champ magnétique \(\vec{B}=B\,\vec{k}\)
et un champ électrique \(\vec{E}=E_1\vec{i}+E_2\vec{j}+E_3\vec{k}\).
Force créée par les champs \(\vec{B}\) et \(\vec{E}\) (force de Lorentz), \(\vec{v}\) et \(\vec{a}\) désignant la vitesse et l'accélération de la particule :
\(\vec{F} = q\vec{v} \wedge \vec{B}+q\vec{E}=m\vec{a}\).
Posons \(\omega=\dfrac{qB}{m}\).
La position \((x(t),y(t),z(t))\) de la particule à l'instant \(t\) vérifie le système différentiel
\[\begin{cases}
x''(t)=\omega y'(t)+\dfrac{q}{m}E_1\\
y''(t) =-\omega x'(t)+\dfrac{q}{m}E_2\\
z''(t) = \dfrac{q}{m}E_3
\end{cases}\]
1er cas : supposons \(\vec{E} =\vec{0}\) et \(\vec{v}_0=x'_0\vec{i}+z'_0\vec{k}\).
\[\begin{cases}\vphantom{\dfrac{q}{m}}
x''(t) = \omega y'(t)\\
y''(t) =-\omega x'(t)\\[1ex]
z''(t) = 0
\end{cases}\]
Solution :
\[\begin{cases}
x(t)=\dfrac{x'_0}{\omega}\sin(\omega t)\\
y(t)=\dfrac{x'_0}{\omega}[\cos(\omega t)-1]\\[1ex]
z(t)=z'_0t
\end{cases}\]
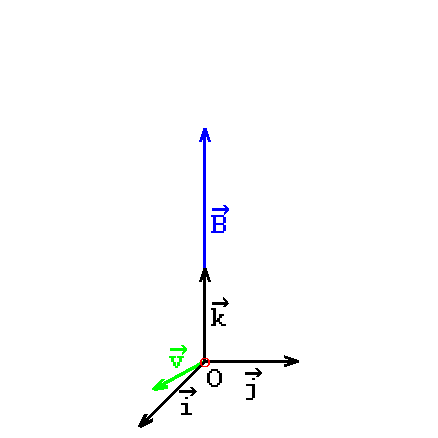
animation 
2e cas : supposons \(\vec{E}\) et \(\vec{B}\) orthogonaux (disons \(\vec{E}=E\vec{j}\)) et \(\vec{v}_0 = \vec{0}\) :
\[\begin{cases}\vphantom{\dfrac{q}{m}}
x''(t) = \omega y'(t)\\
y''(t) =-\omega x'(t)+\dfrac{q}{m}E\\[1ex]
z''(t) = 0
\end{cases}\]
Solution : en posant \(a=\dfrac{mE}{qB^2}\) :
\[\begin{cases}\vphantom{\dfrac{q}{m}}
x(t) = a[\omega t-\sin(\omega t)]\\
y(t) = a[1-\cos(\omega t)]\\[1ex]
z(t) = 0
\end{cases}\]
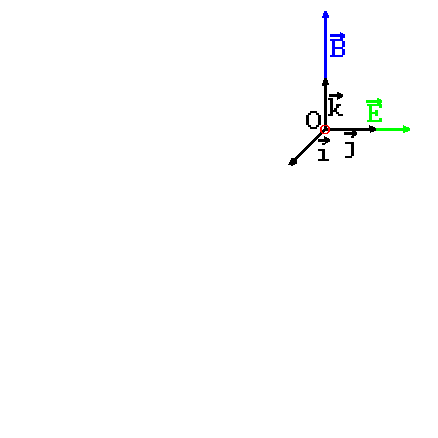
animation 
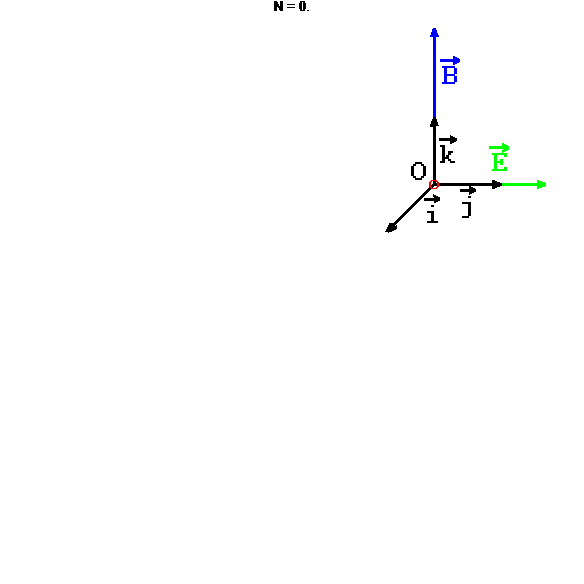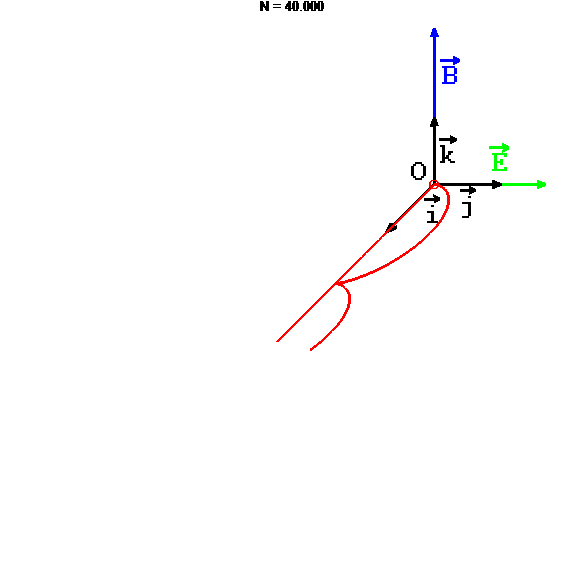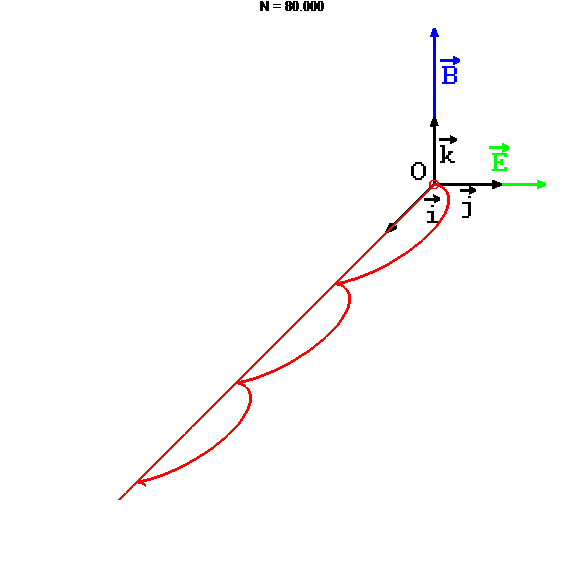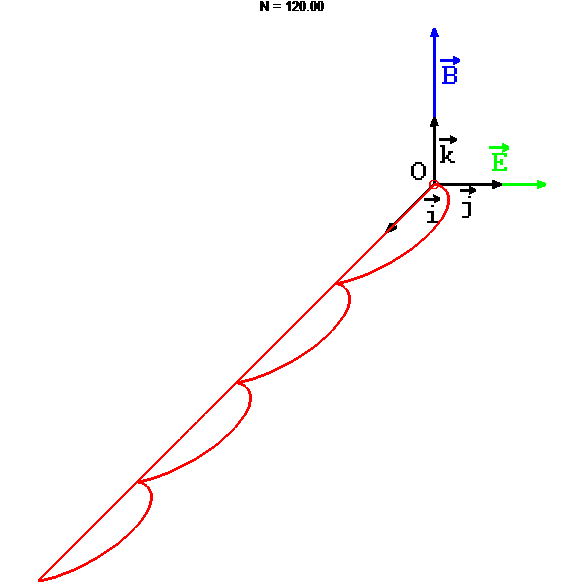
stop 
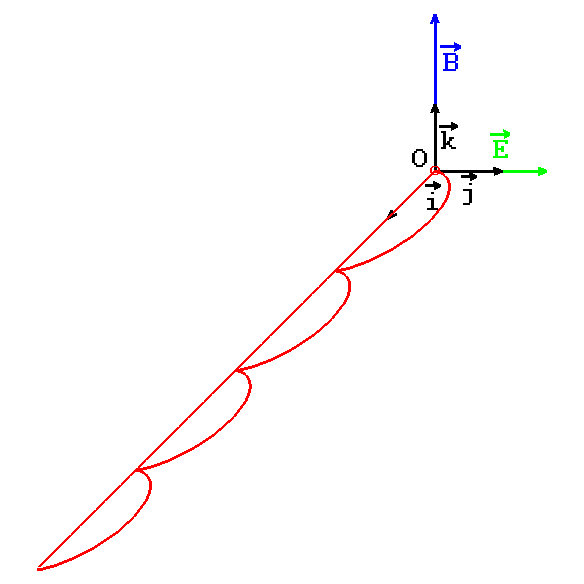
Cycloïde dans le plan xOy
Un peu d'optique/acoustique : \(\vphantom{a_a}\)caustiques de cercle
Rayons issus d'une source ponctuelle
se réfléchissant sur une surface circulaire
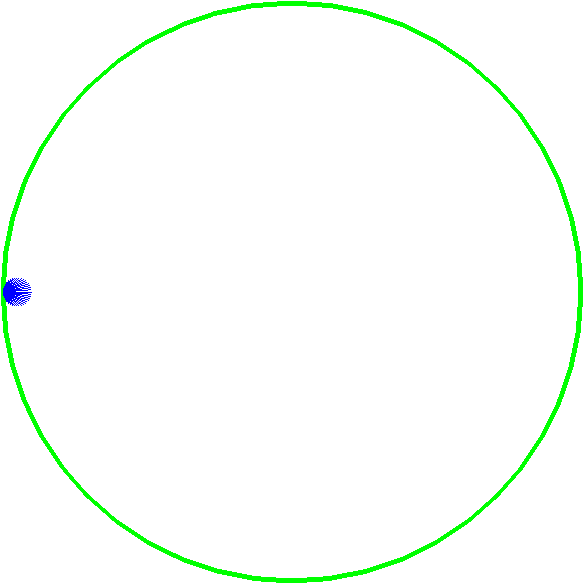
animation 

Un micro unidirectionnel : le micro cardioïde
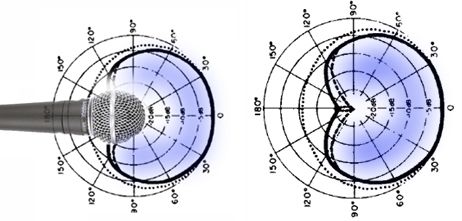
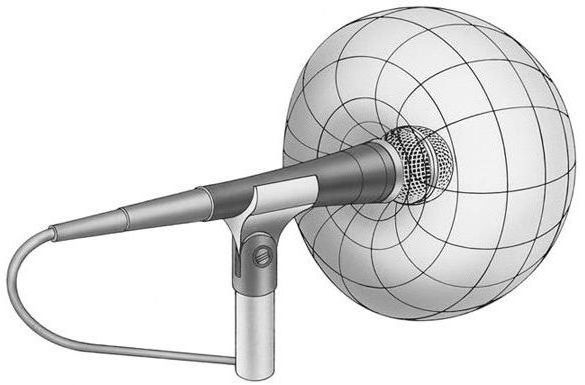
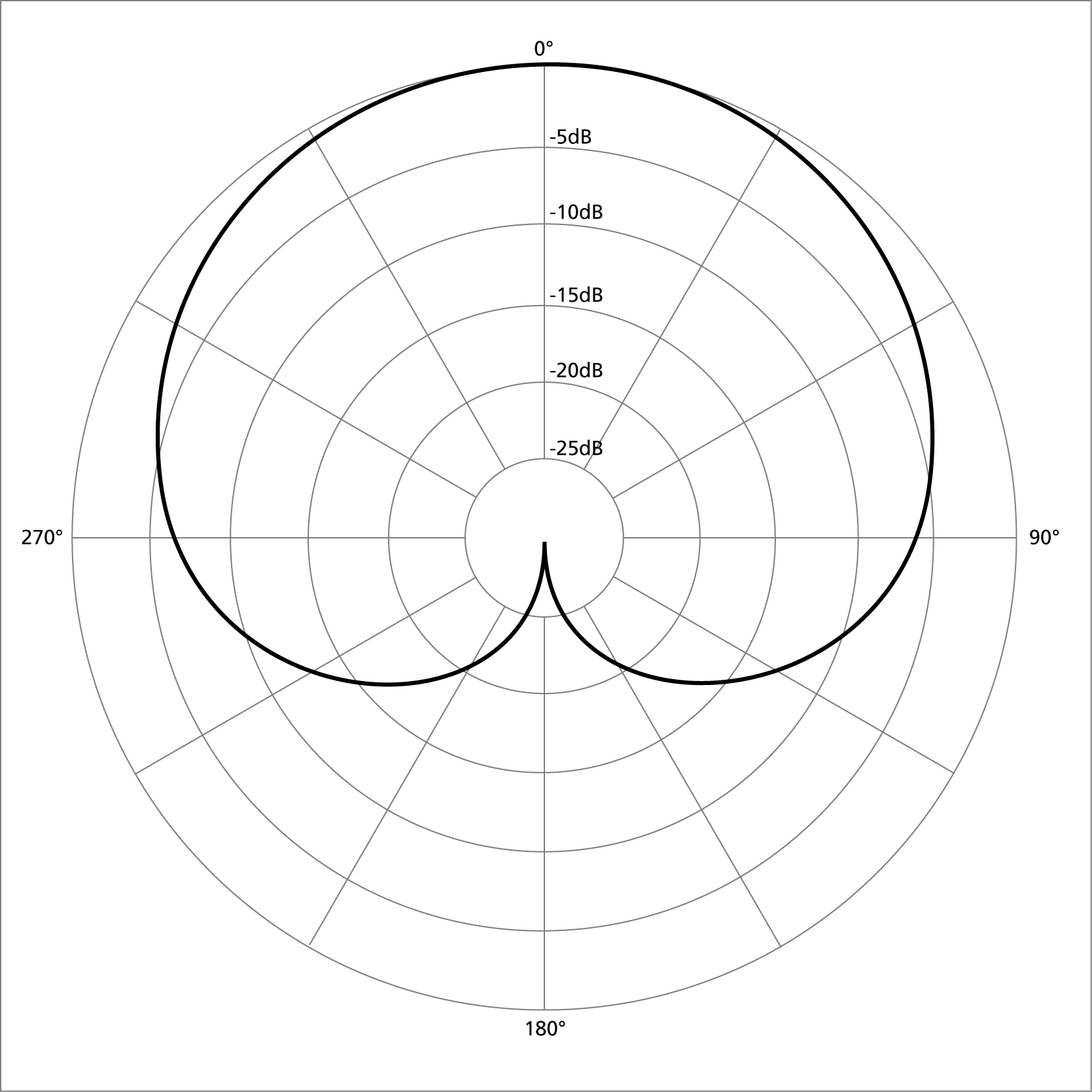 |
|
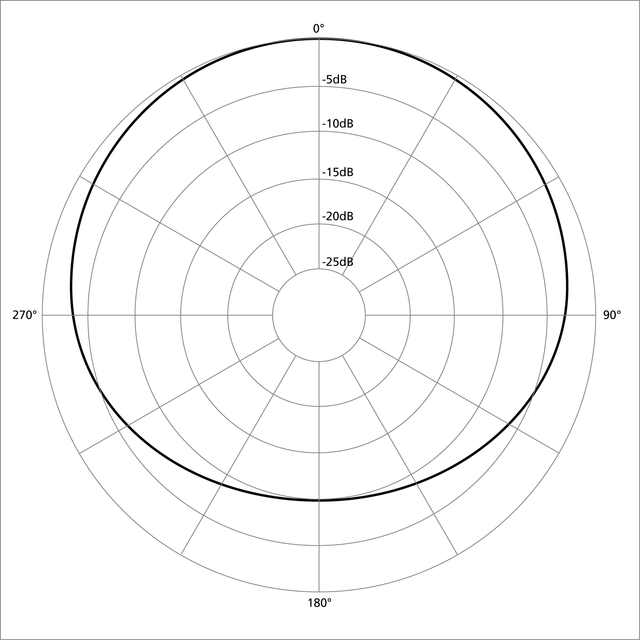 |
| cardioïde |
|
sous-cardioïde |
|
 |
|
 |
| hyper-cardioïde |
|
sur-cardioïde |
Rayons issus d'une source à l'infini
se réfléchissant sur une surface circulaire
animation 
Un peu de magie : \(\vphantom{a_q}\)mélanges parfaits de cartes
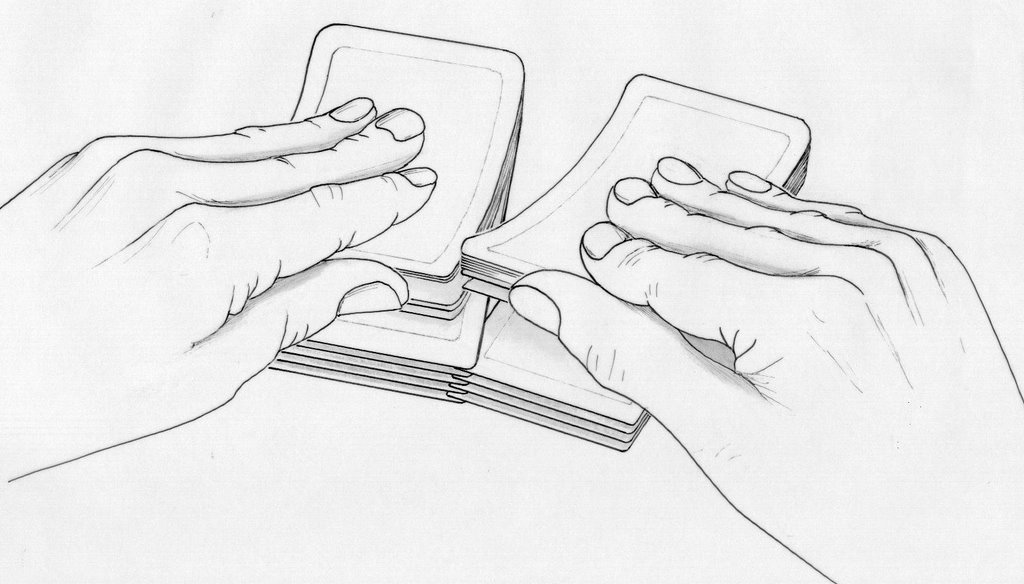
Évolution de la première carte
lors de plusieurs mélanges consécutifs
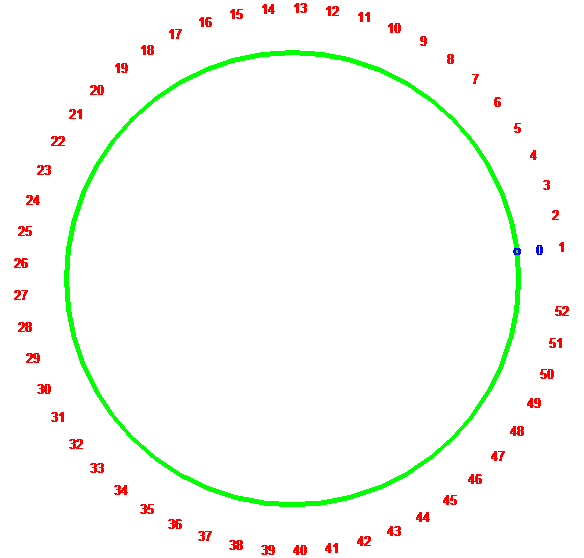
1er mélange 
Un peu de mécanique :
engrenages
Moteur Wankel


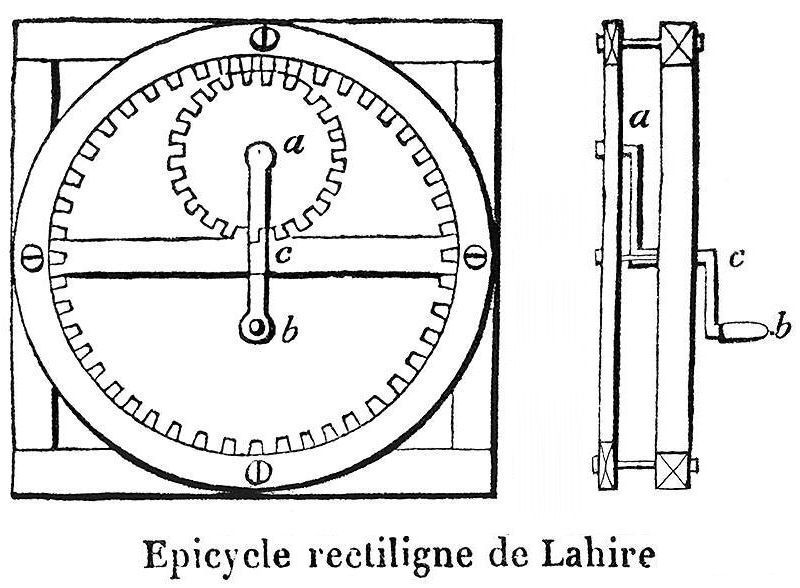
Un engrenage cylindrique intérieur :
l'épicycle de La Hire
 |
| Philippe de la Hire |
| (1640–1718) |
Mathématicien, physicien,
astronome français |
–––––––––
Chambre de combustion d'un moteur Wankel


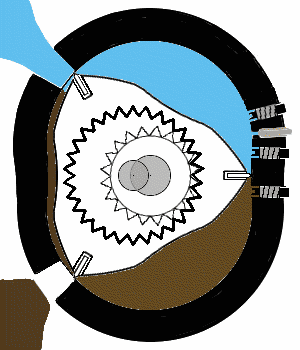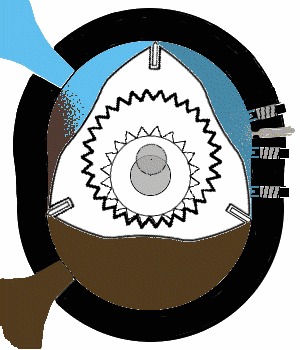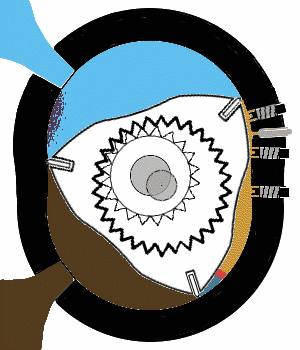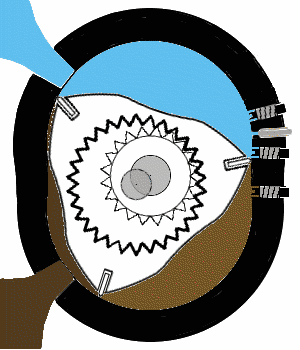
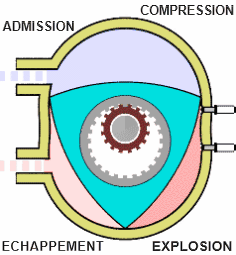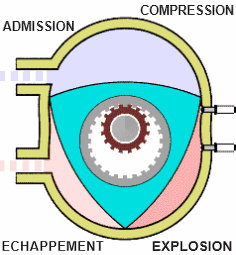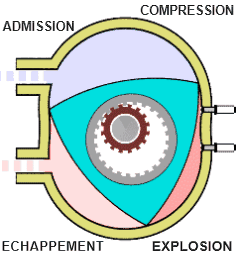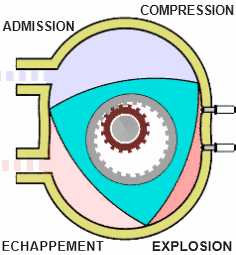
Une chambre de combustion néphroïdale
 |
| Felix Heinrich Wankel |
| (1902–1988) |
| Ingénieur allemand |
 |
 |
Mazda RX8 |
Mazda 787B |
 |
 |
NSU Spider |
Mercedes C111 |
Un peu d'astronomie : épicycles
\(\vphantom{a_a}\)Orbites planétaires
Épicycle
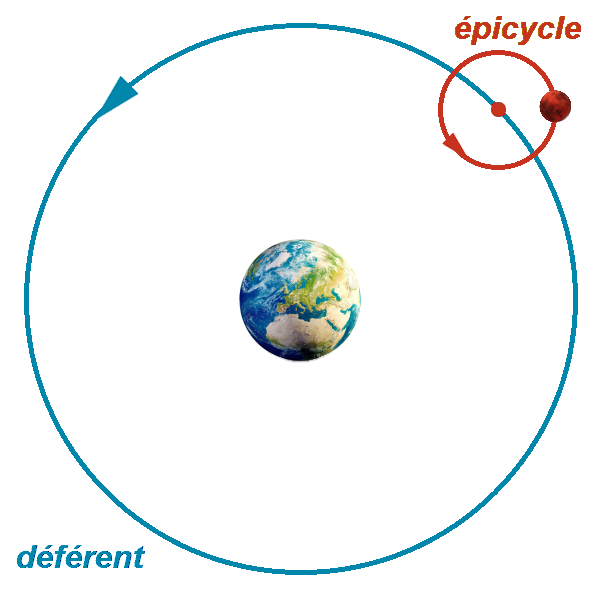
La planète se déplace
selon une trajectoire circulaire (épicycle)
Le centre de ce cercle tourne autour de la Terre
décrivant une autre trajectoire circulaire (déférent)
Paramétrisation :
cercle rotatif de rayon \(r\) (épicycle)
de centre évoluant sur un cercle de rayon \(R\) (déférent)
\(x(t)=R\cos(\Omega t)+r\cos(\omega t\!+\!\varphi)\)
\(y(t)=R\sin(\Omega t)+r\sin(\omega t\!+\!\varphi)\)
ou encore
|
\(z(t)=R\,\mathrm{e}^{\mathrm{i}\Omega t}\hspace{0em}
+\hspace{0em}r\,\mathrm{e}^{\mathrm{i}(\omega t+\varphi)}\)
|
Orbite héliocentrique de la Lune

orbite héliocentrique Terre :
\(z_T = R_T \mathrm{e}^{\mathrm{i}2\pi t/T_T}\vphantom{\frac{a}{q}}\)
orbite héliocentrique Lune :
\(z_L = R_T\mathrm{e}^{\mathrm{i}2\pi t/T_T}+r_{\!\raise -0.5ex L}\mathrm{e}^{\mathrm{i}2\pi t/T_T+\mathrm{i}2\pi t/t_L}\)
avec
rayon orbital Terre (autour du Soleil) :
\(R_T = 149\, 597\, 887\) km
période de révolution Terre (autour du Soleil) :
\(T_T = 365,25\) jours
rayon orbital Lune (autour de la Terre) :
\(r_{\!\raise -0.5ex L} = 384\, 399\) km
période de révolution Lune
(autour de la Terre) :
\(t_L = 27,3\) jours
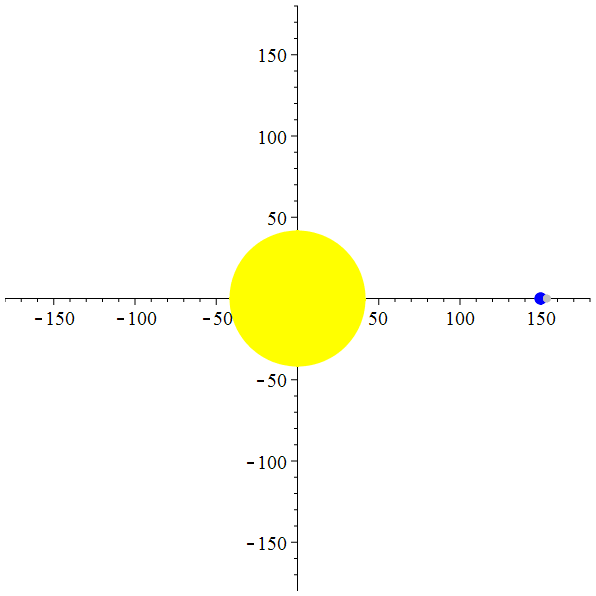
animation 
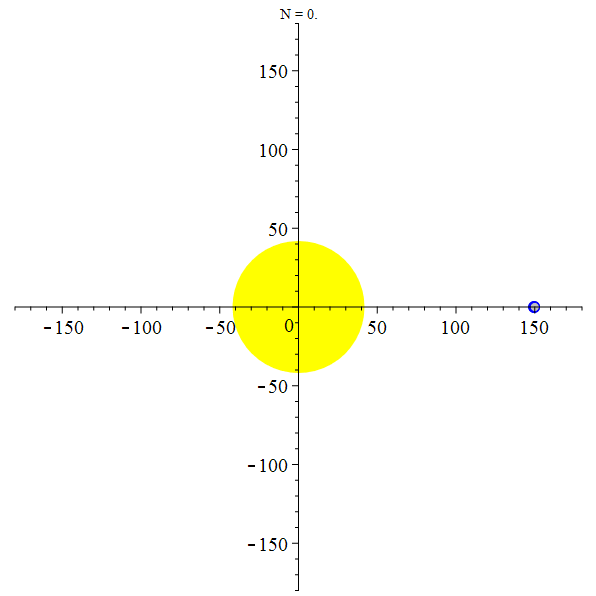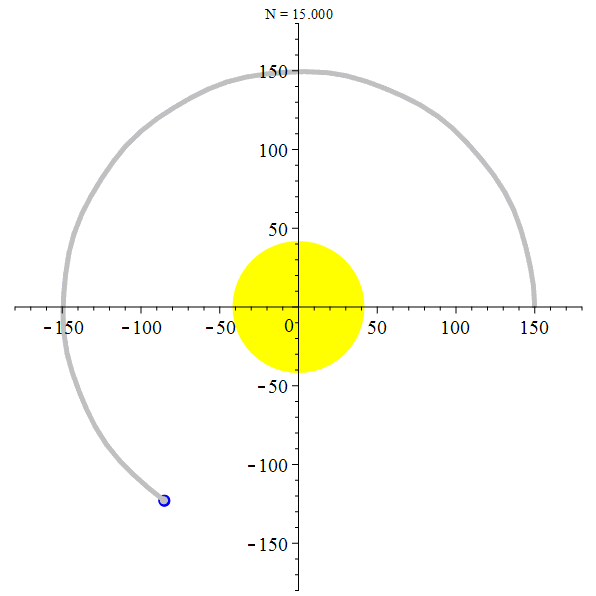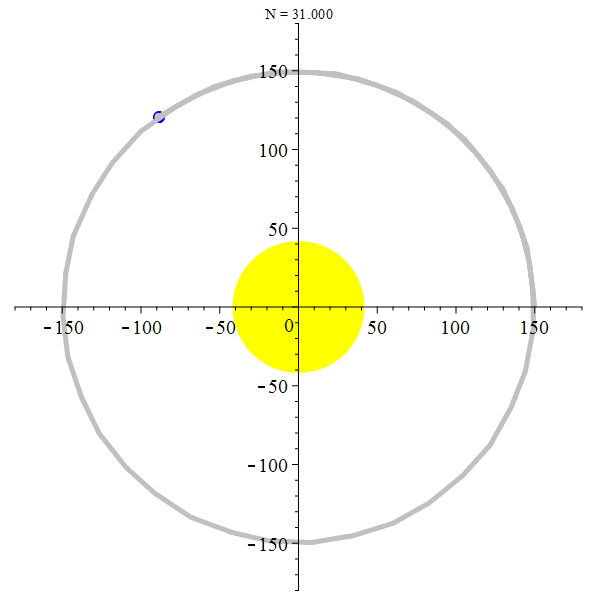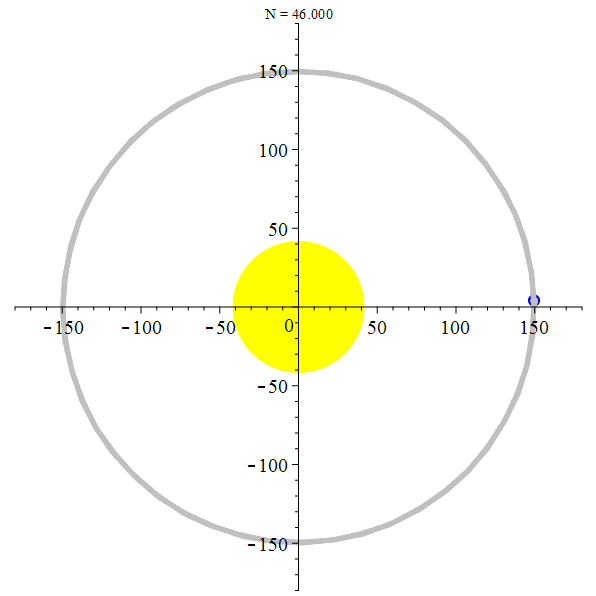
stop 
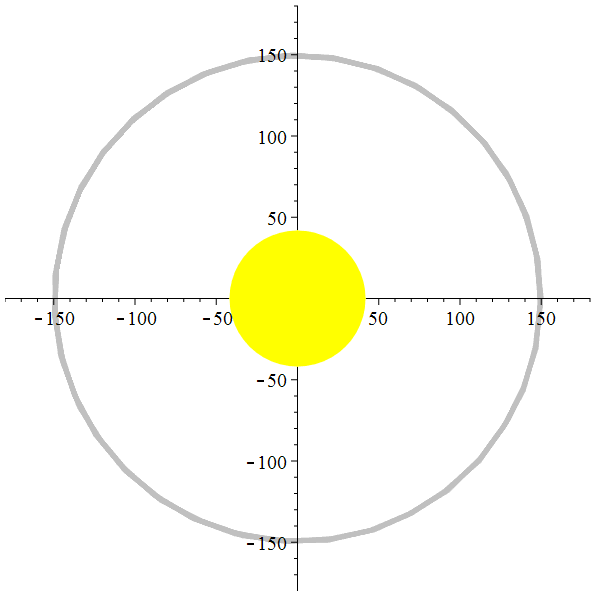
La Terre et la Lune autour du Soleil
Et si la lune était 10 fois plus éloignée de la terre…
animation 
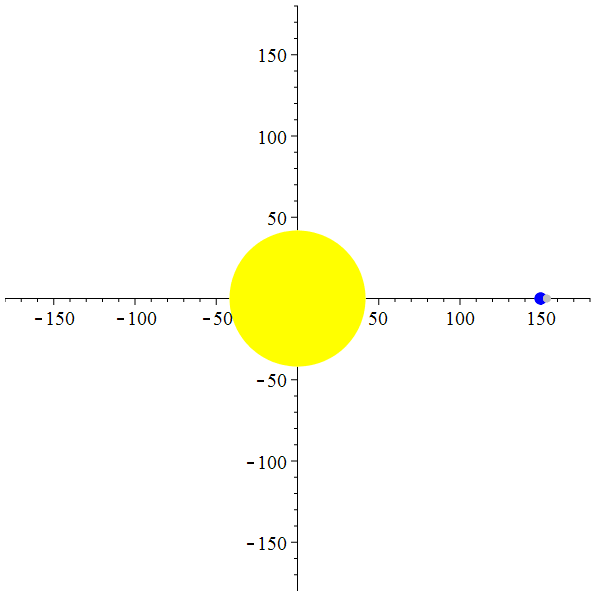
Et si la lune était 20 fois plus éloignée de la terre…
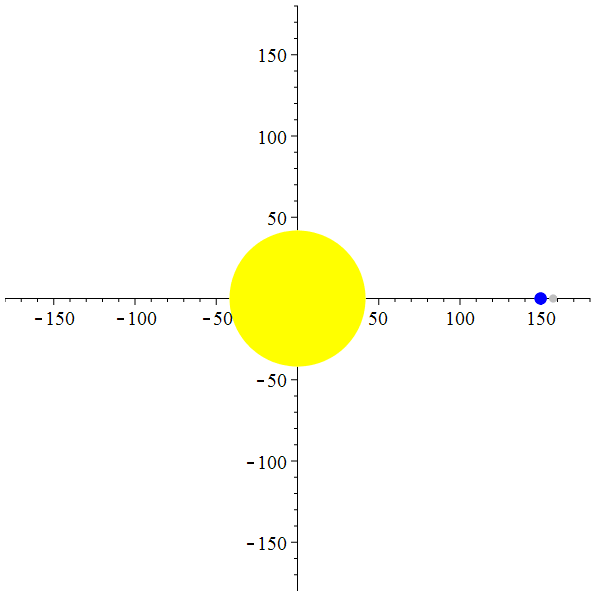
animation 
Et si la lune était 50 fois plus éloignée de la terre…
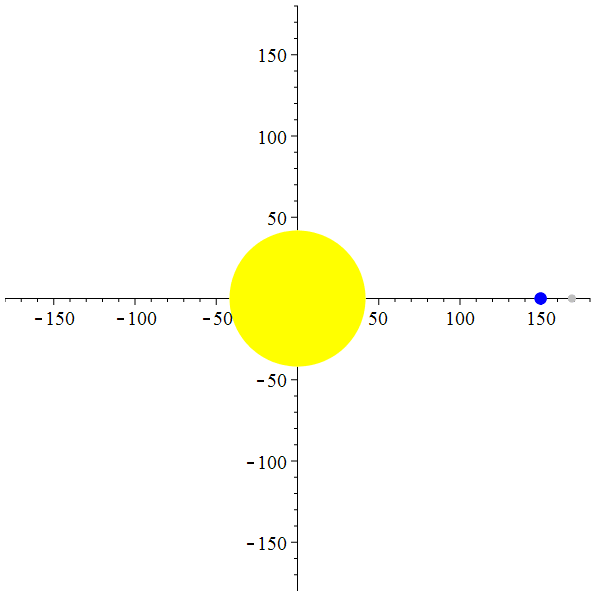
animation 
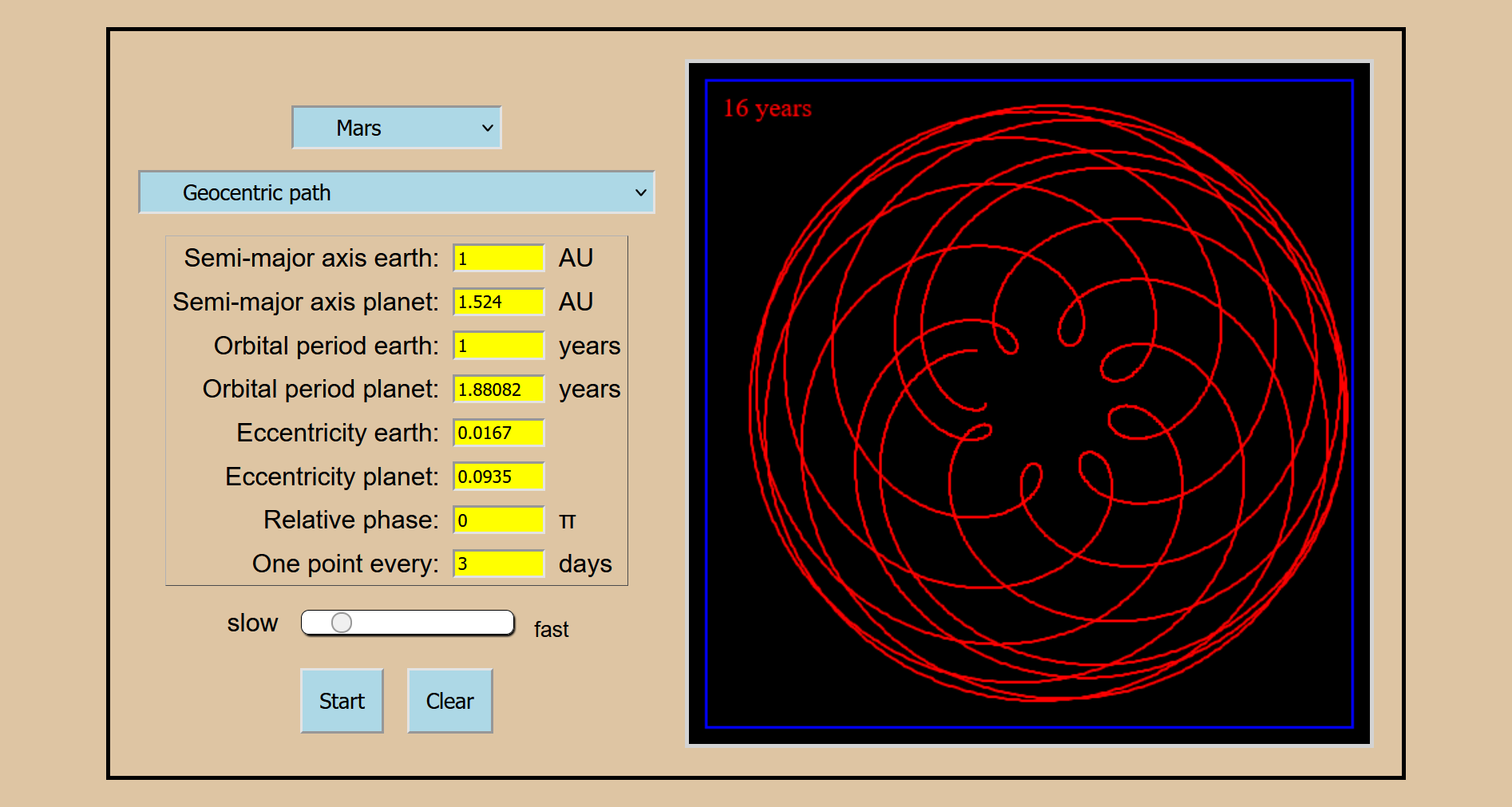
Orbite géocentrique de Mars
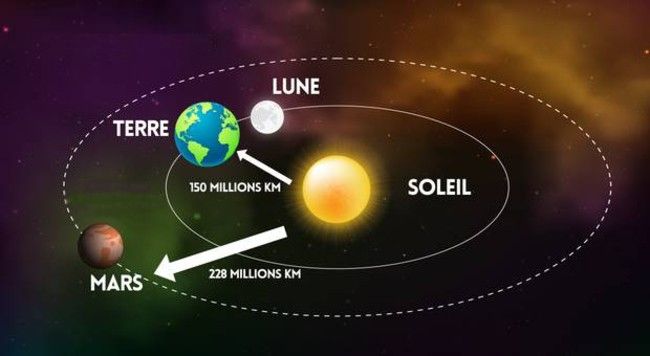
orbite héliocentrique Terre :
\(z_T = R_T \mathrm{e}^{\mathrm{i}2\pi t/T_T}\vphantom{\frac{a}{q}}\)
orbite héliocentrique Mars :
\(z_M = R_M \mathrm{e}^{\mathrm{i}2\pi t/T_M}\)
orbite géocentrique Soleil :
\(z_S =-R_T \mathrm{e}^{\mathrm{i}2\pi t/T_T}\vphantom{\frac{a}{q}}\)
orbite géocentrique Mars :
\(z_M = R_M \mathrm{e}^{\mathrm{i}2\pi t/T_M}-R_T \mathrm{e}^{\mathrm{i}2\pi t/T_T}\)
avec
rayon orbital Terre (autour du Soleil) :
\(R_T = 149\, 597\, 887\) km
période de révolution Terre (autour du Soleil) :
\(T_T = 365,25\) jours
rayon orbital Mars (autour du Soleil) :
\(R_M = 227\, 936\, 637\) km
période de révolution Mars (autour du Soleil) :
\(T_M = 686,9\) jours
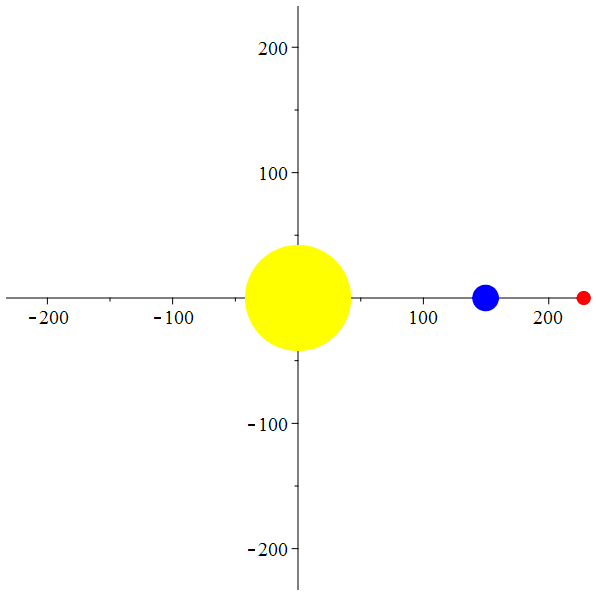
animation 
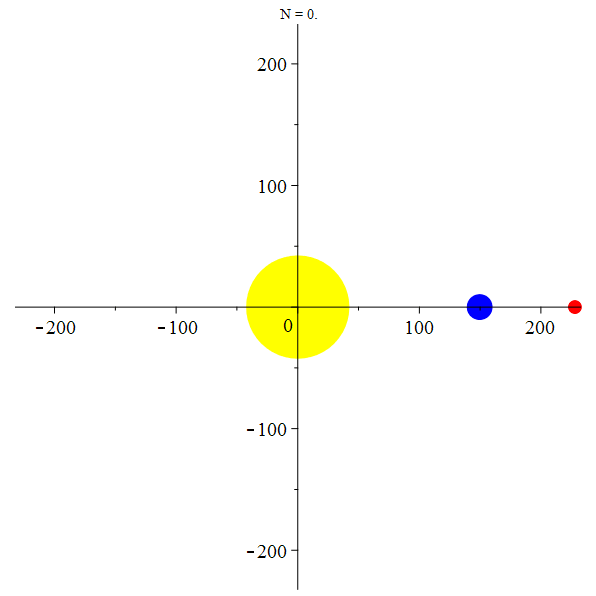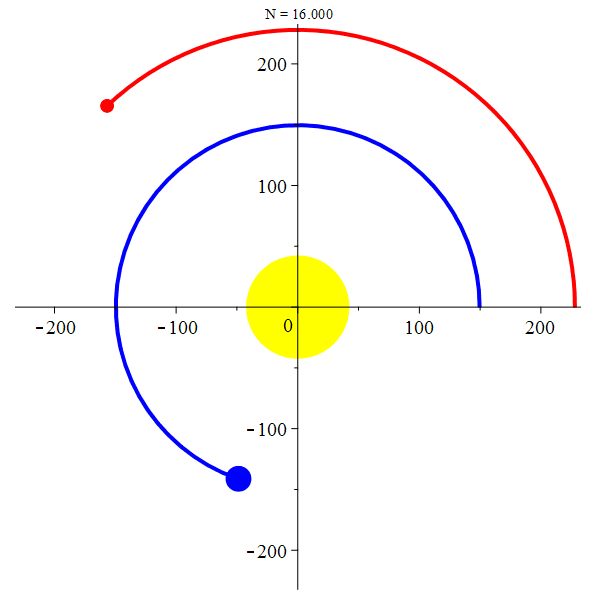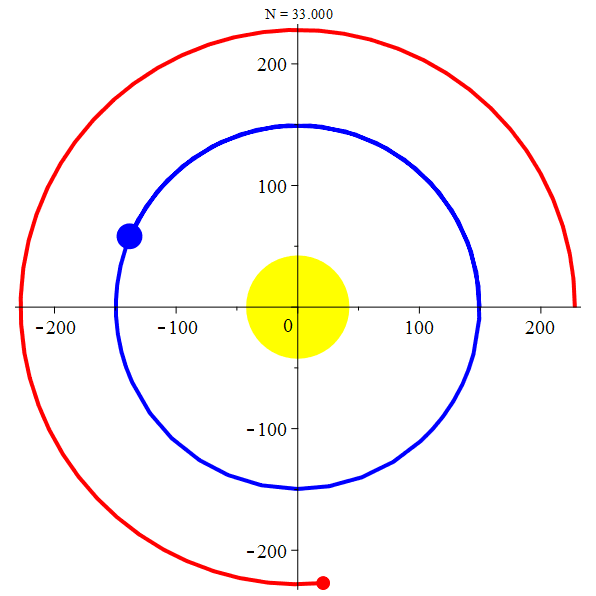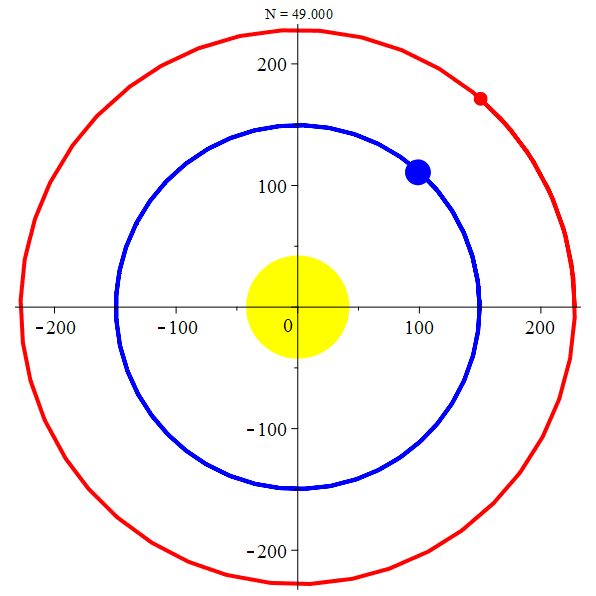
stop 
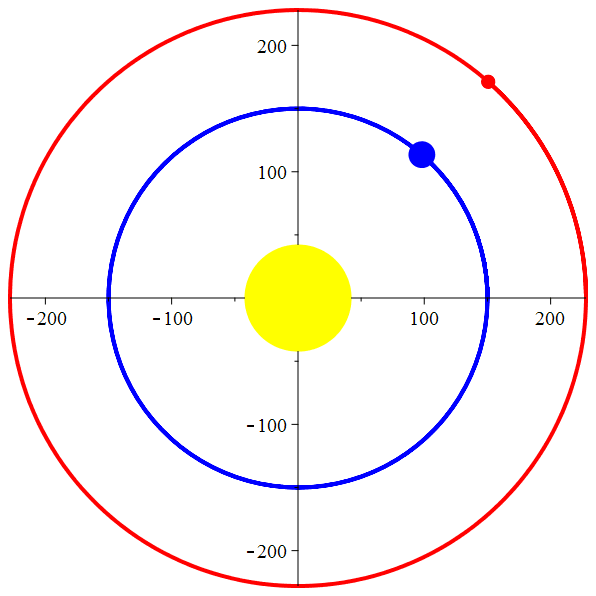
La Terre et
Mars autour du
Soleil
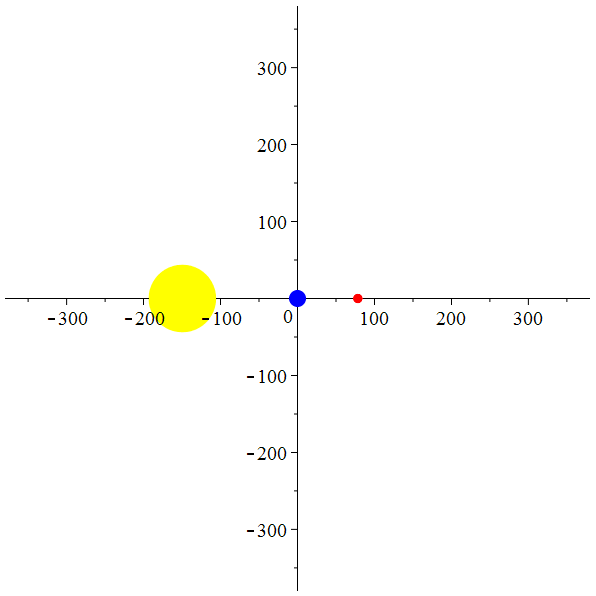
animation 
Le système solaire
| Planète | rayon orbital | période
de révolution |
|
| Mercure | \(57\,909\,176\) km | \(87,9\) jours |
| Vénus | \(108\,208\,930\) km | \(224,7\) jours |
| Terre | \(149\,597\,887\) km | \(365,25\) jours |
| Mars | \(227\,936\,637\) km | \(686,9\) jours |
| Jupiter | \(778\,412\,027\) km | \(4\,335,3\) jours |
| Saturne | \(1\,421\,179\,772\) km | \(10\,757,7\) jours |
| Uranus | \(2\,876\,679\,082\) km | \(30\,799,1\) jours |
| Neptune | \(4\,503\,443\,661\) km | \(60\,224,9\) jours |
Orbites héliocentriques
(en millions de km)
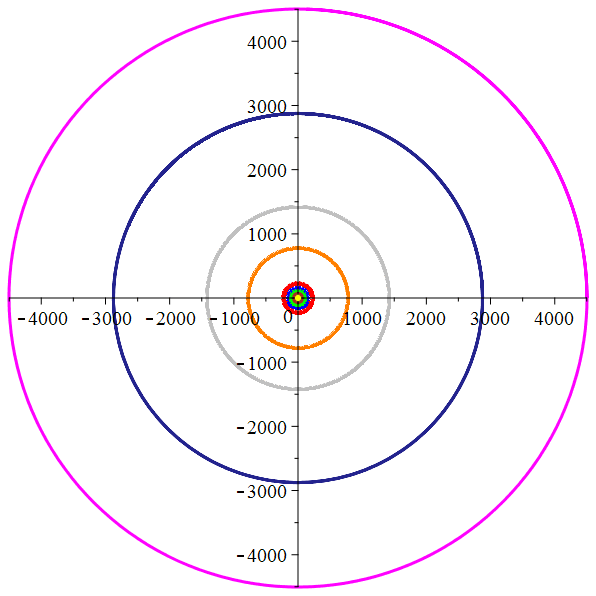
Mercure,
Vénus,
Terre, Mars,
Jupiter,
Saturne, Uranus
et Neptune
autour du Soleil
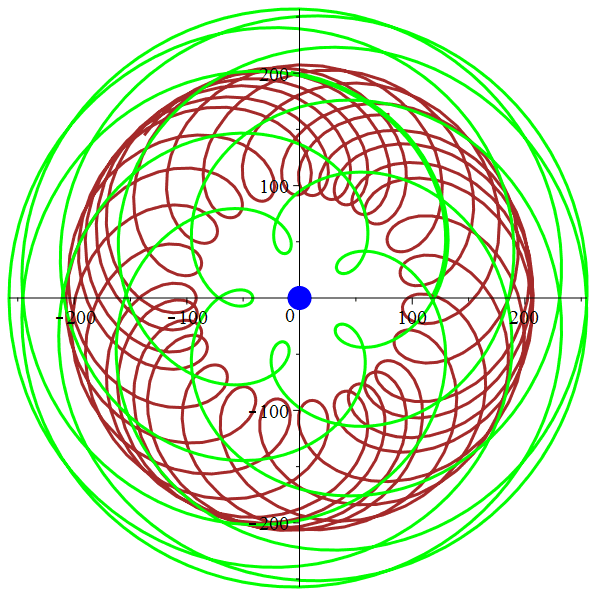
Orbites géocentriques
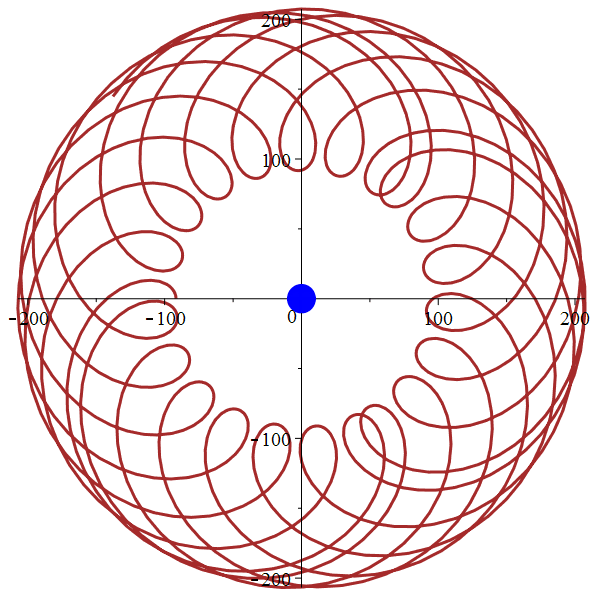
Mercure
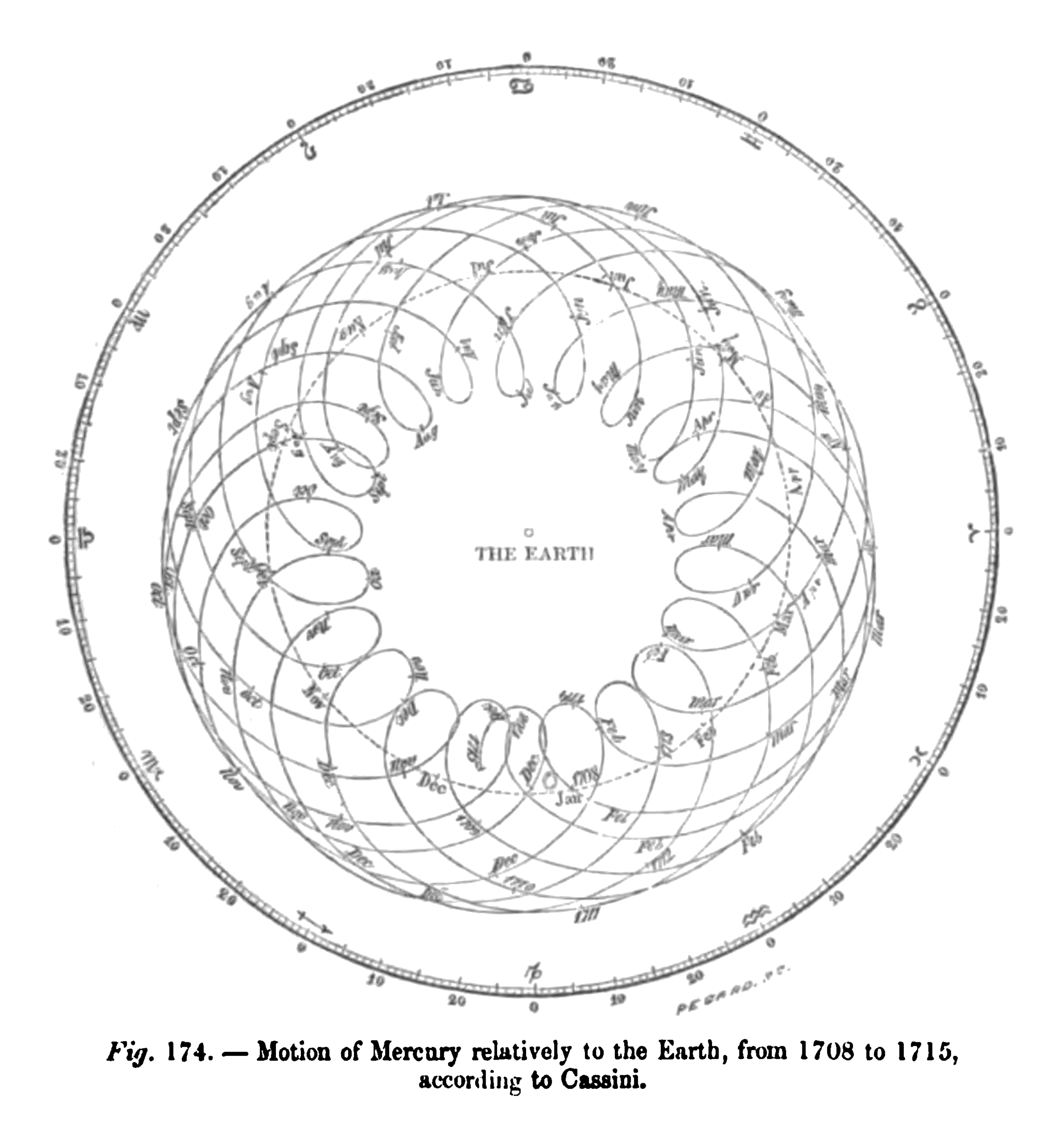
Mercure (par Cassini, 1708)
Mercure,
Vénus
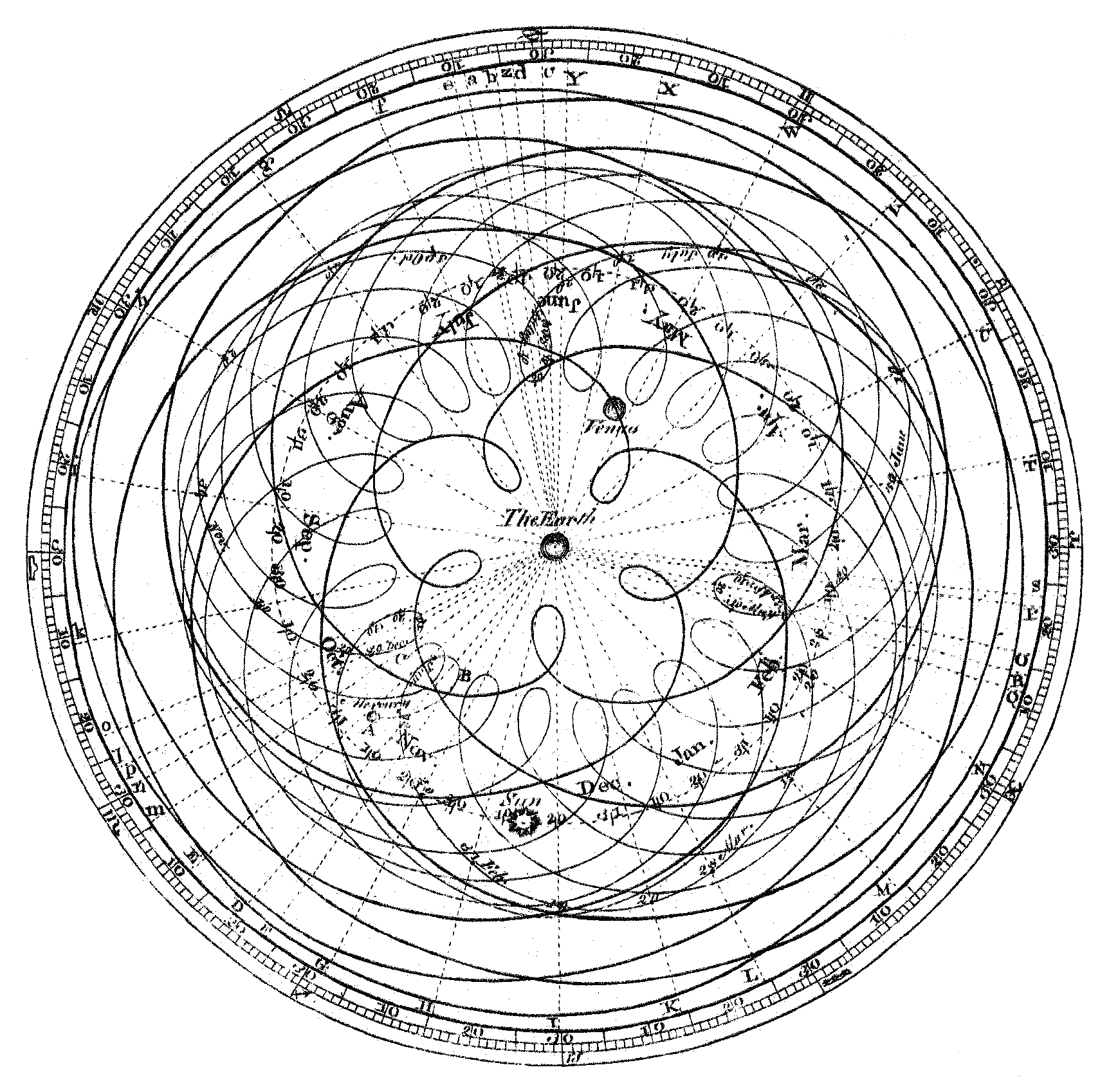
Mercure et Vénus (par Cassini, 1708)
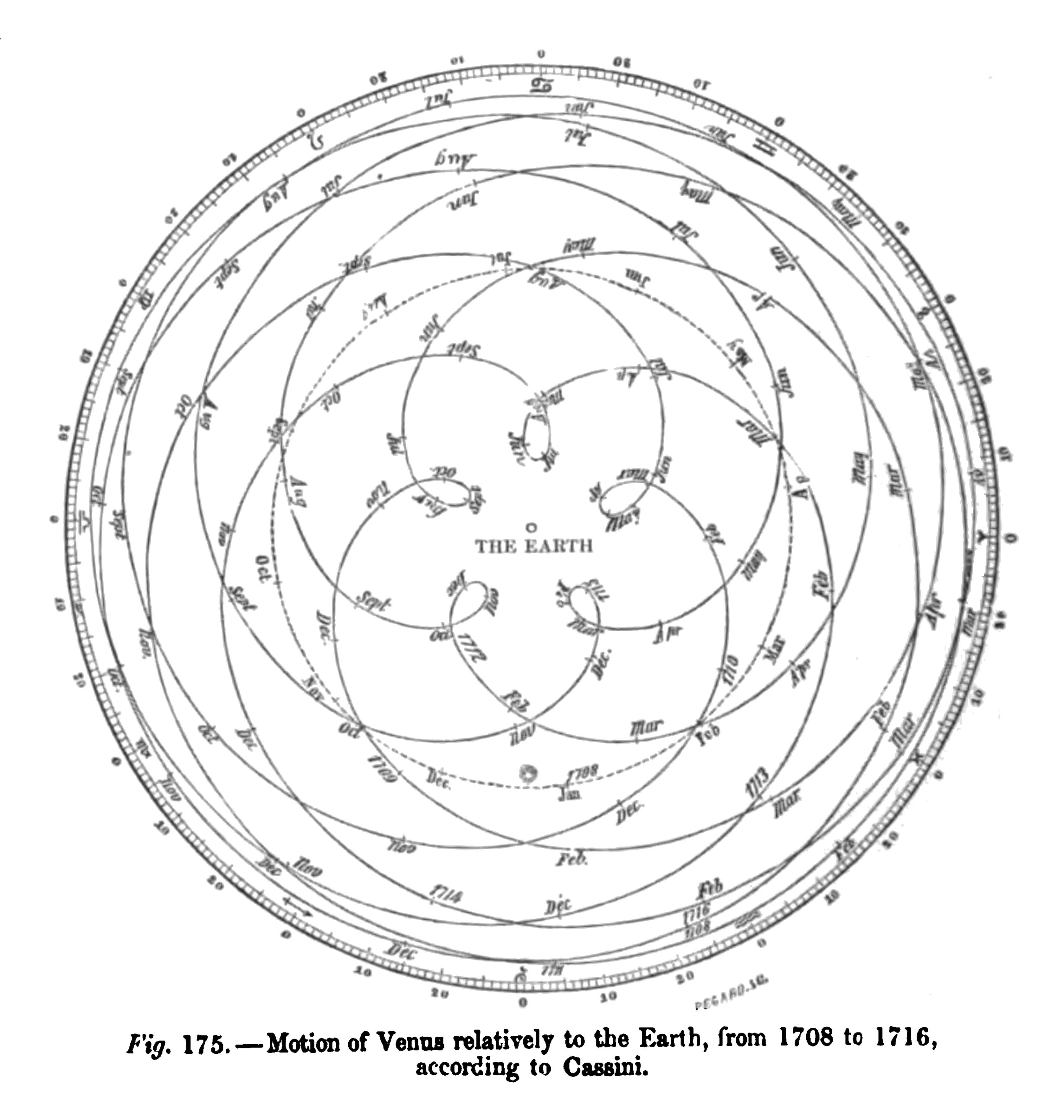
Venus (par Cassini, 1708)
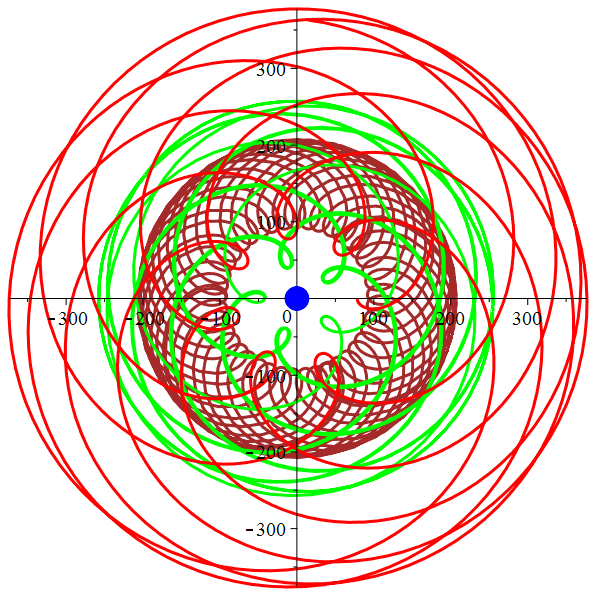
Mercure,
Vénus, Mars
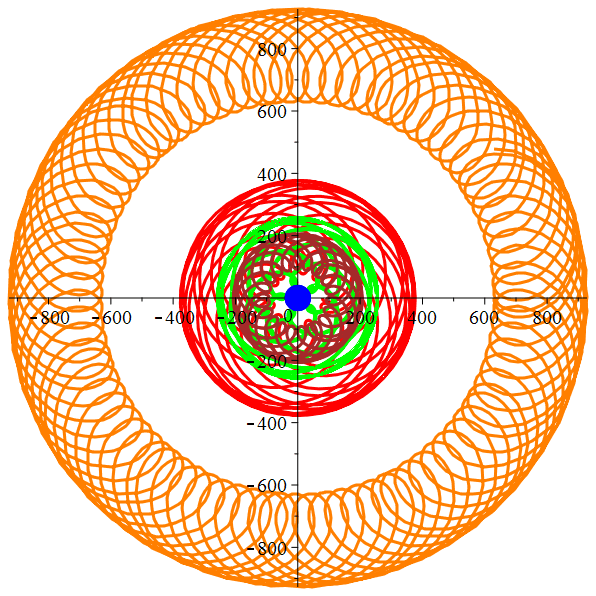
Mercure, Vénus,
Mars, Jupiter
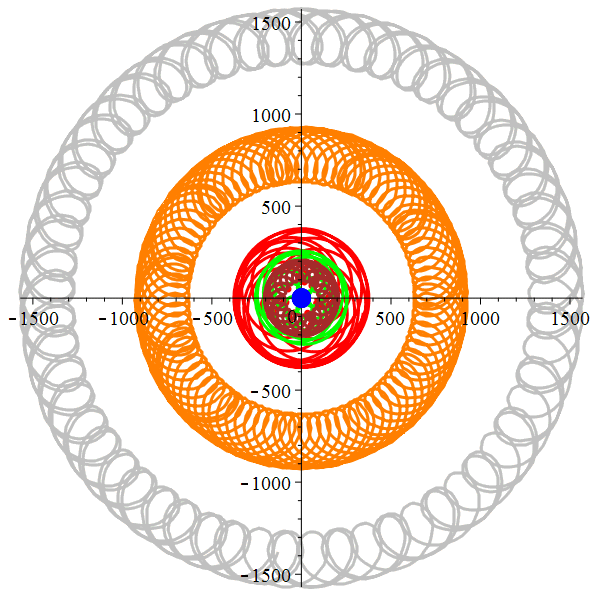
Mercure,
Vénus,
Mars,
Jupiter, Saturne
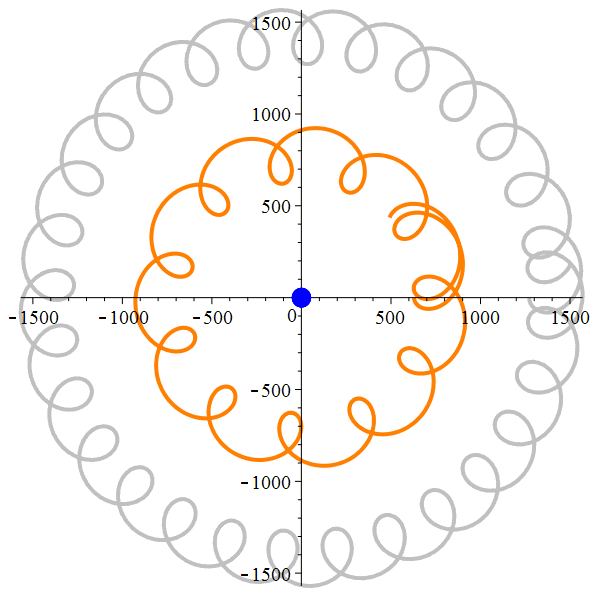
Jupiter,
Saturne
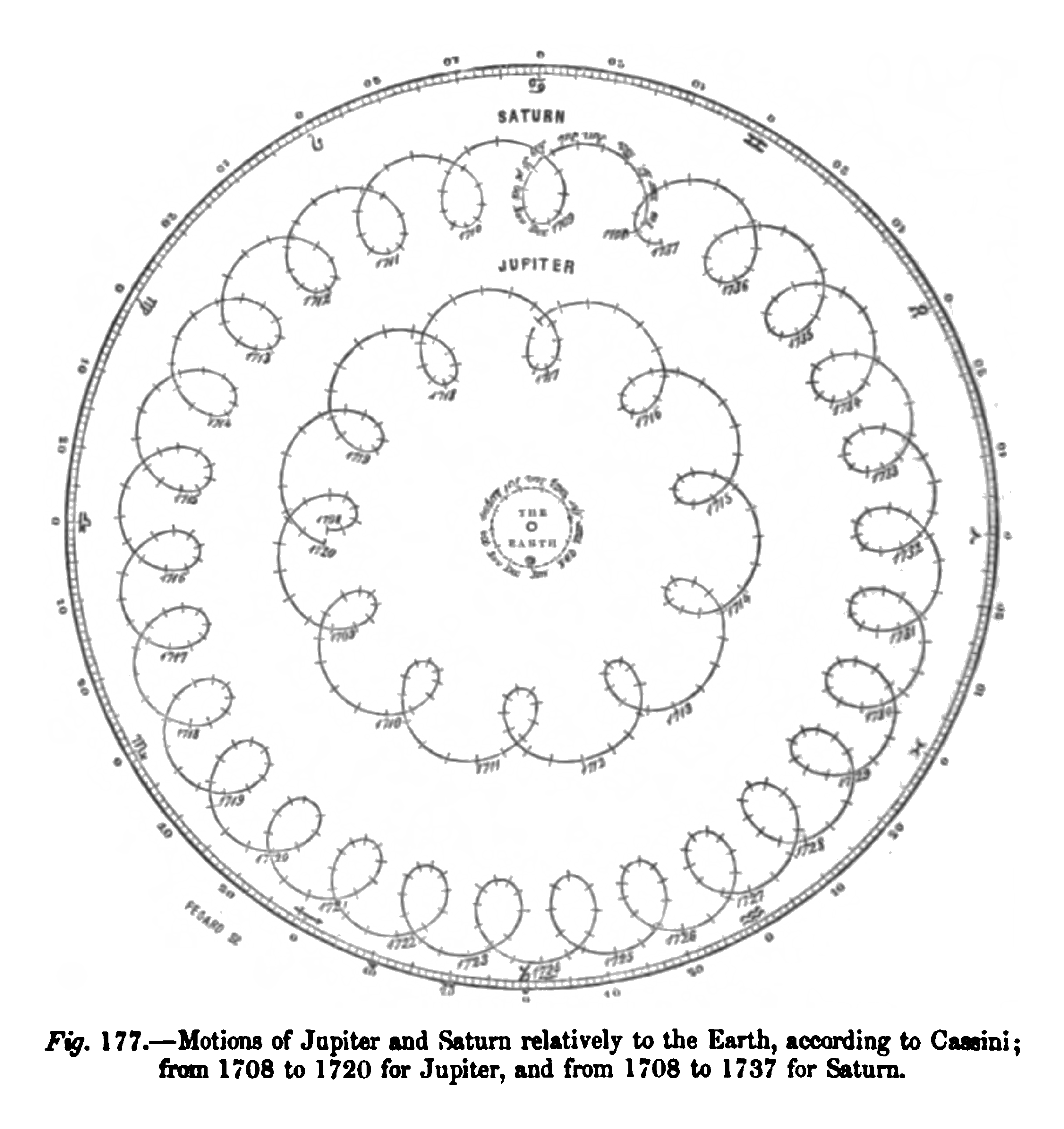
Jupiter et Saturne
(par Cassini, 1708)
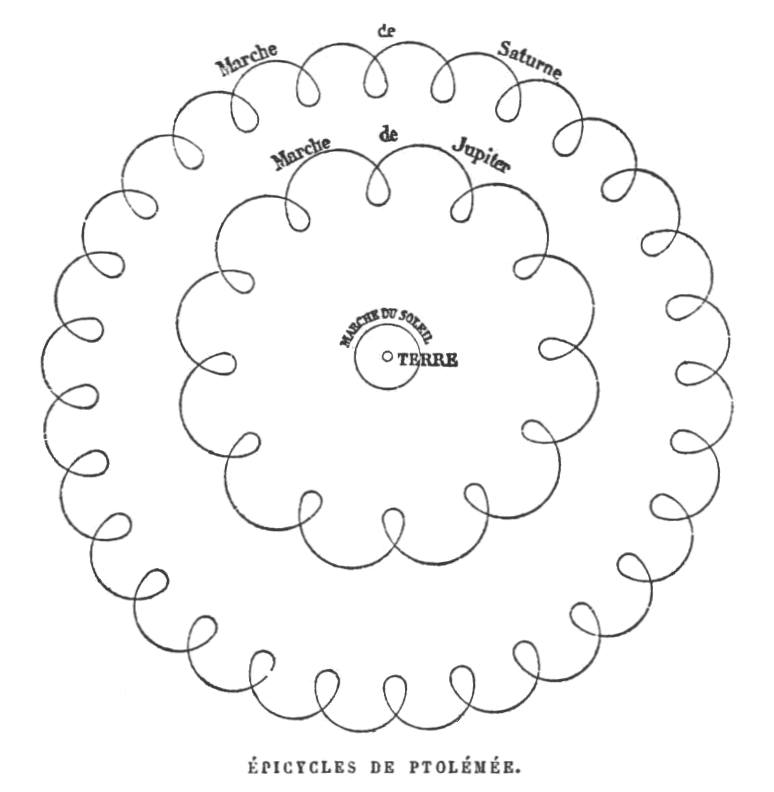
Jupiter et Saturne
(par Ptolémée)
 |
| Claude Ptolémée |
| (100–168) |
| Astronome et astrologue grec |
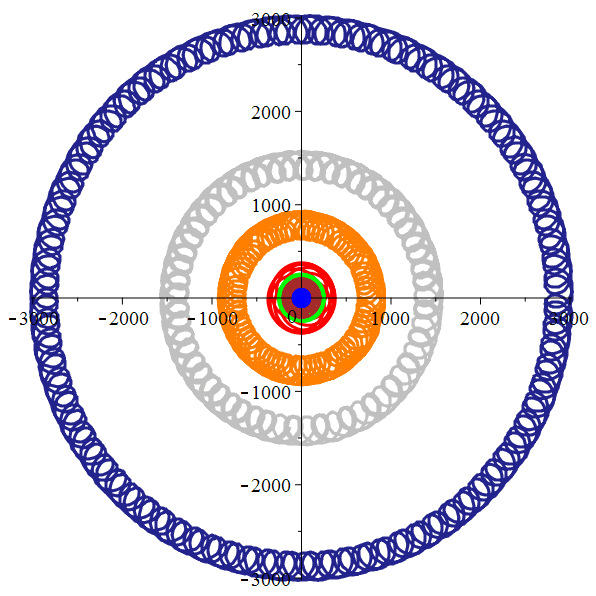
Mercure,
Vénus,
Mars,
Jupiter, Saturne,
Uranus
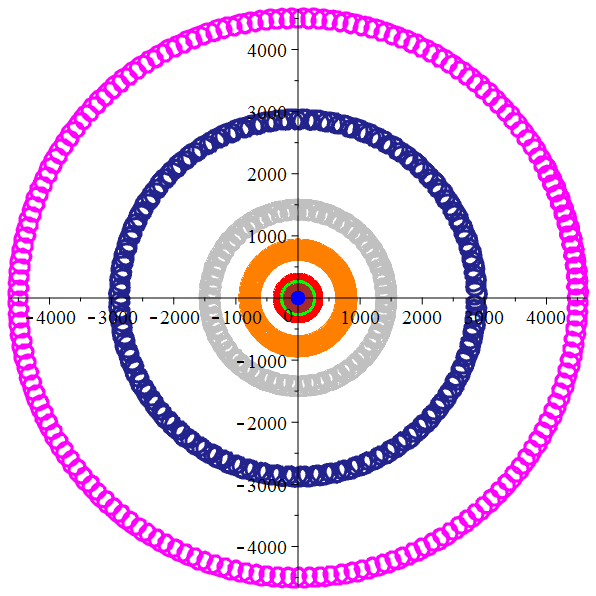
Mercure,
Vénus,
Mars,
Jupiter, Saturne,
Uranus,
Neptune
Satellites de Jupiter

Io, Europe,
Ganymède, Callisto
| Planète | rayon orbital | période
de révolution |
|
| Io | \(421\,800\) km | \(1,8\) jours |
| Europe | \(671\,100\) km | \(3,5\) jours |
| Ganymède | \(1\,070\,400\) km | \(7,1\) jours |
| Callisto | \(1\,882\,700\) km | \(16,7\) jours |
Orbite héliocentrique de
Io
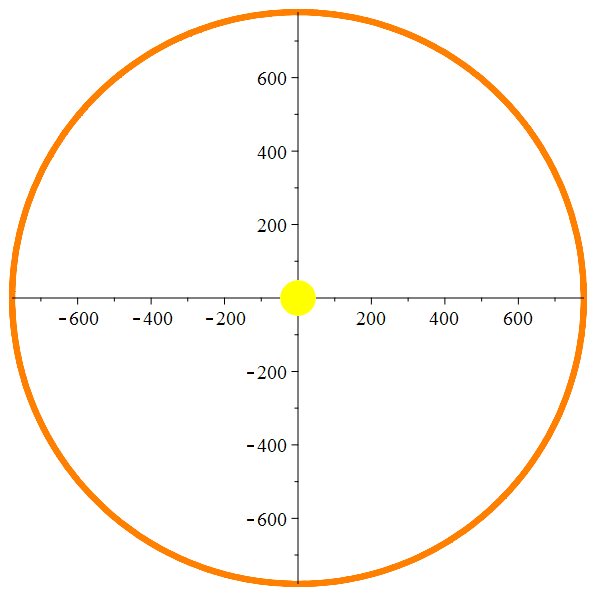
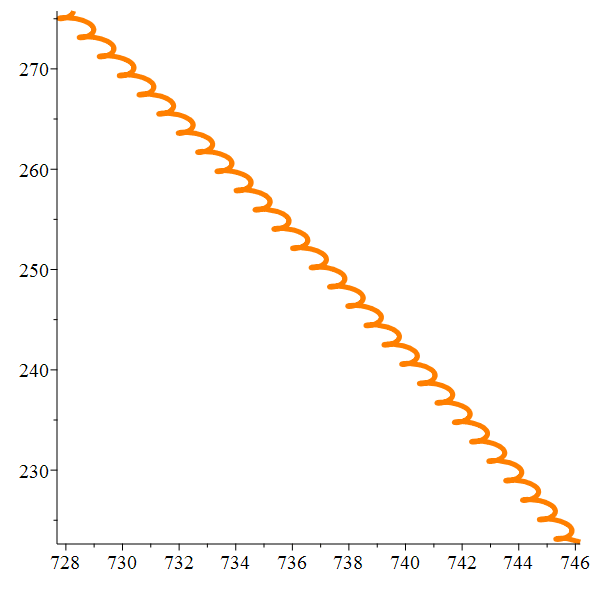
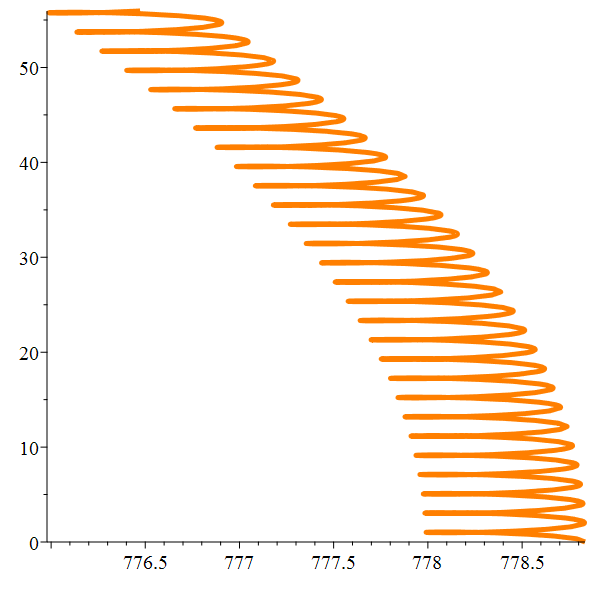
Zoom
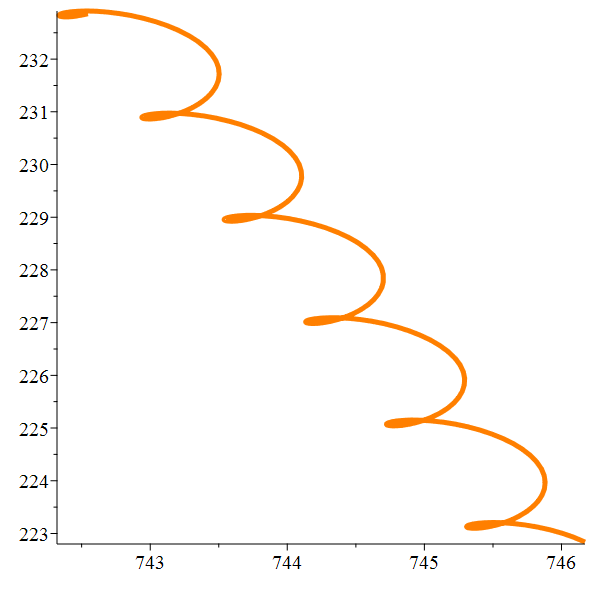
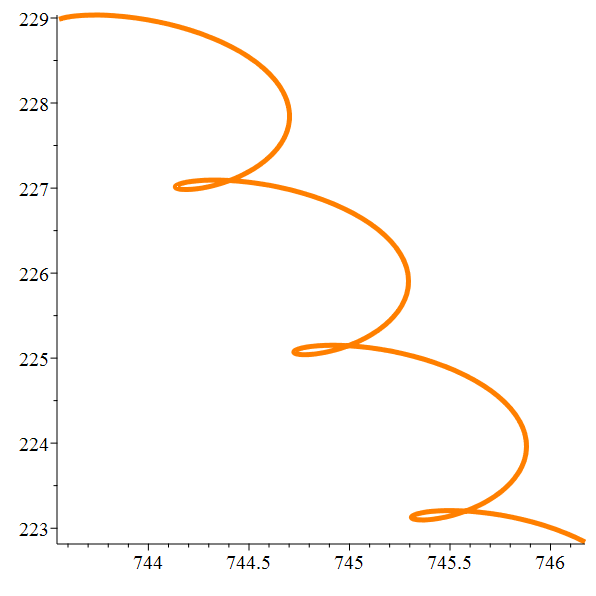
Méga-zoom
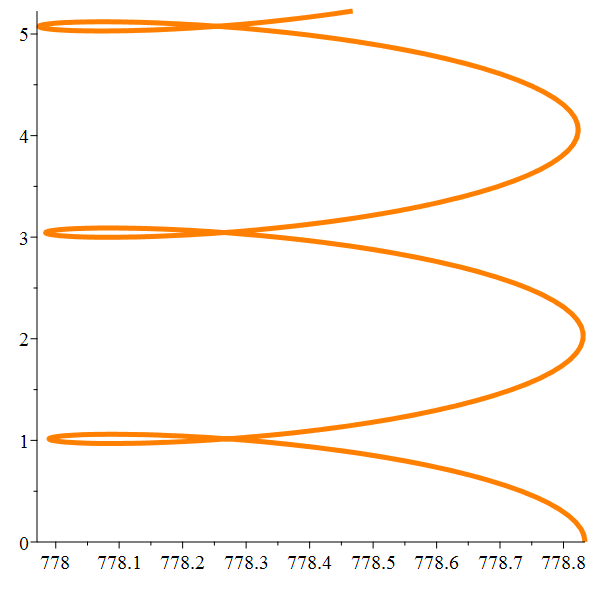
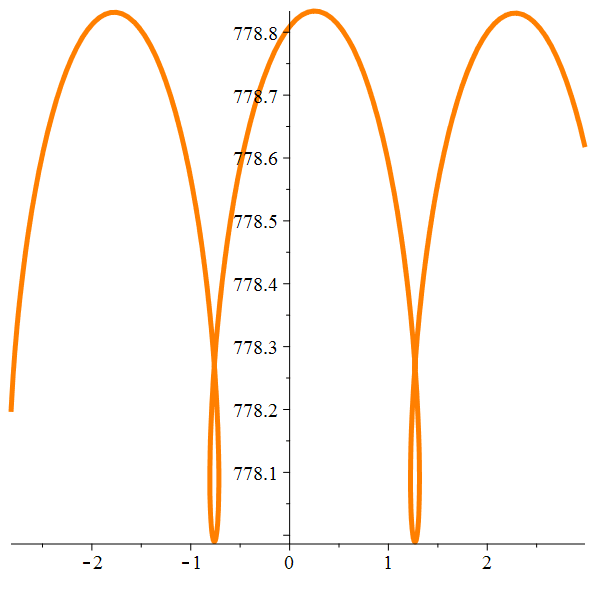
Giga-zoom
Orbite héliocentrique de Europe
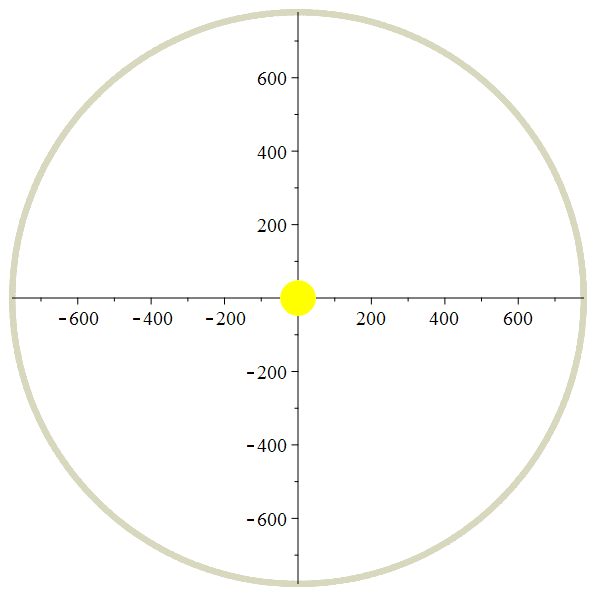
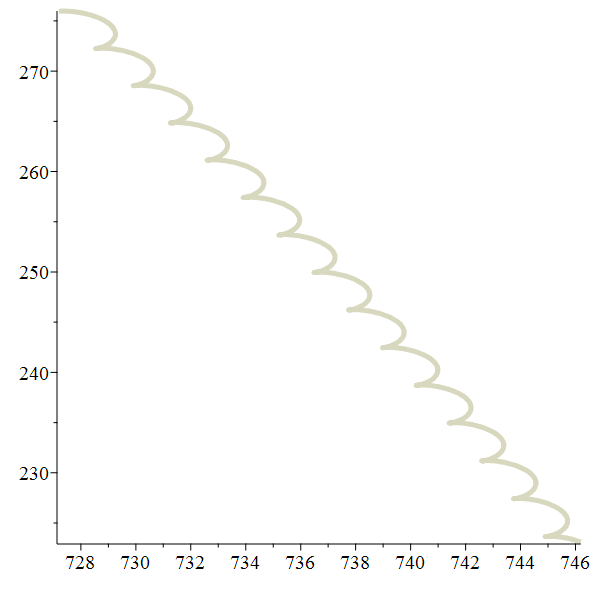
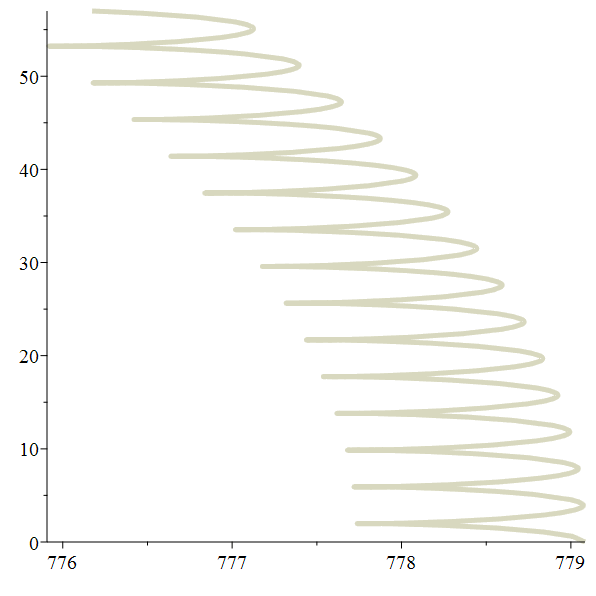
Zoom
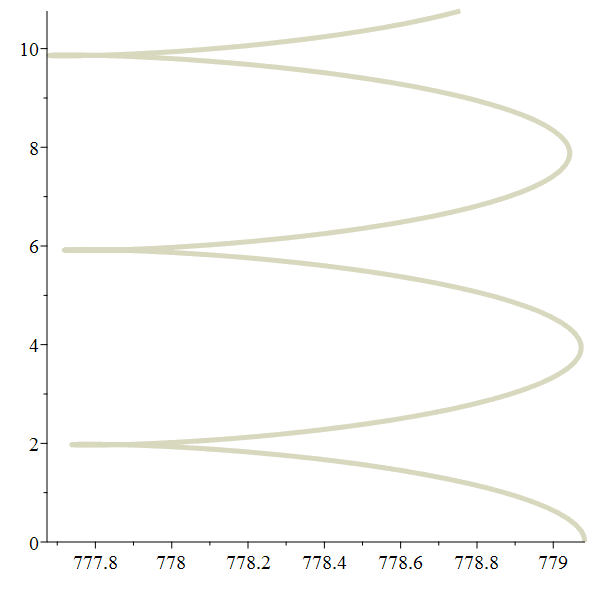
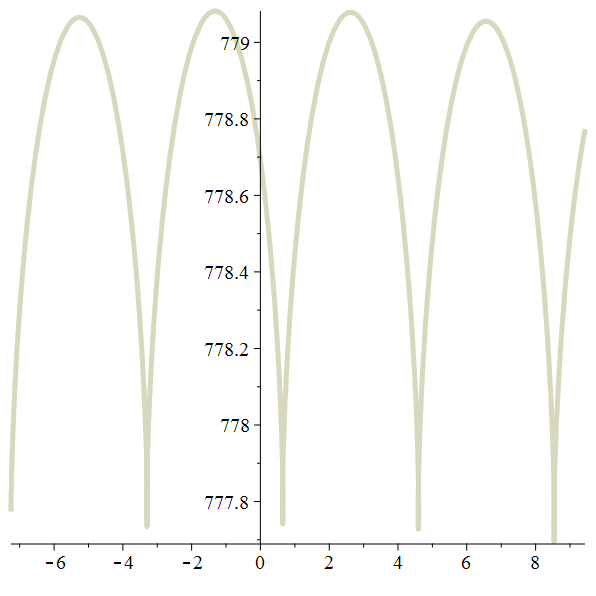
Méga-zoom
Orbite héliocentrique
de Ganymède
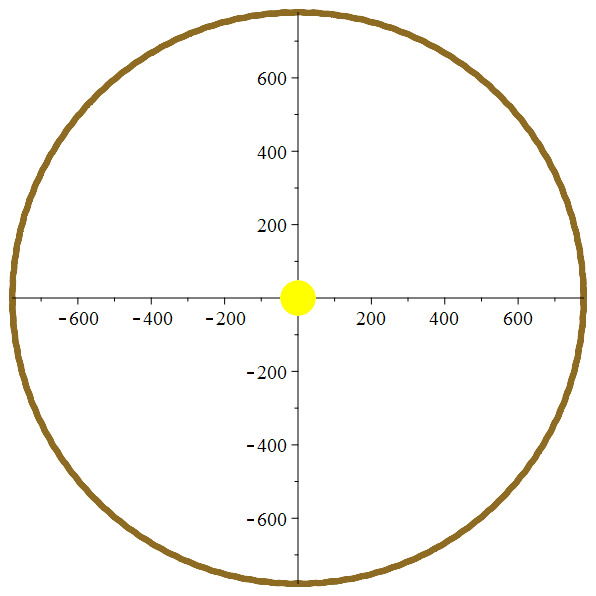
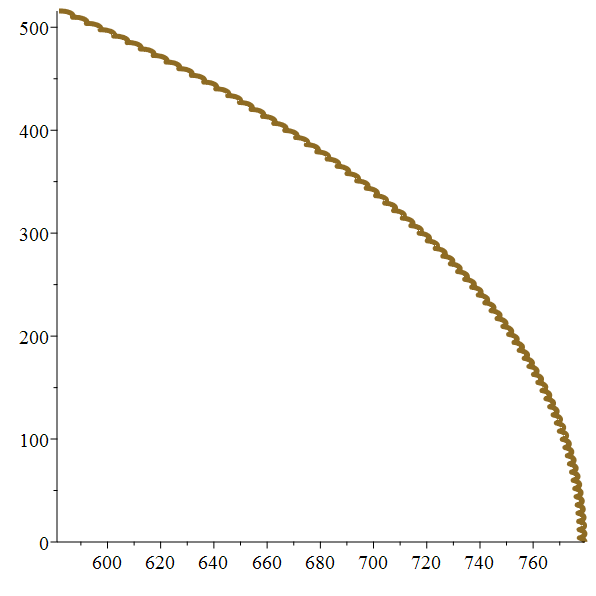
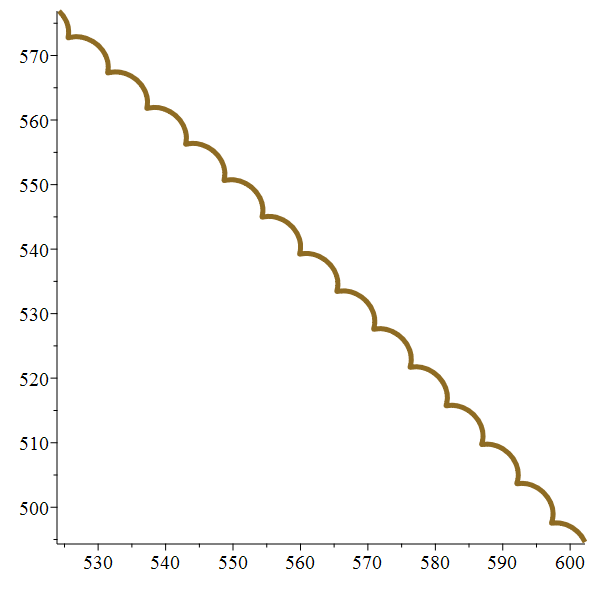
Zoom
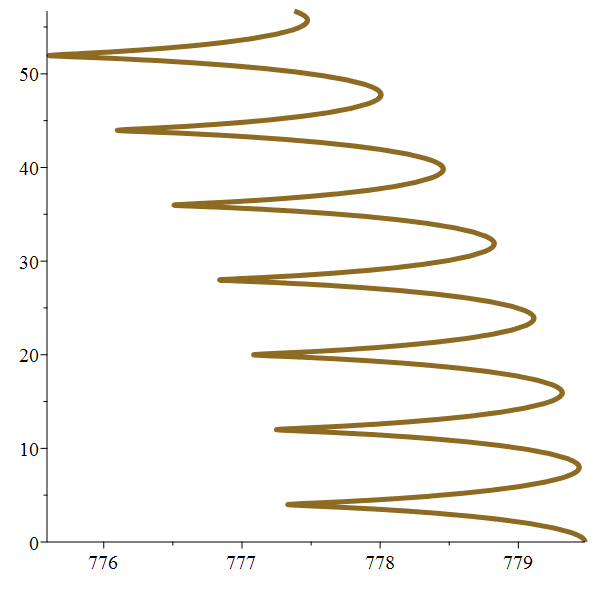
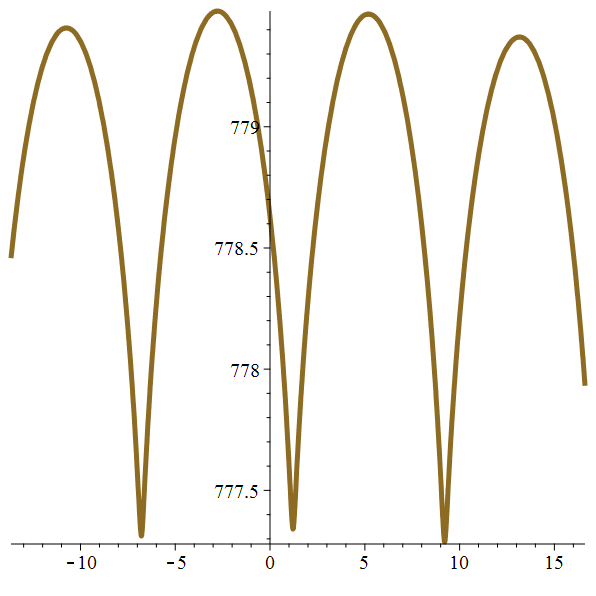
Méga-zoom
Orbite héliocentrique
de Callisto
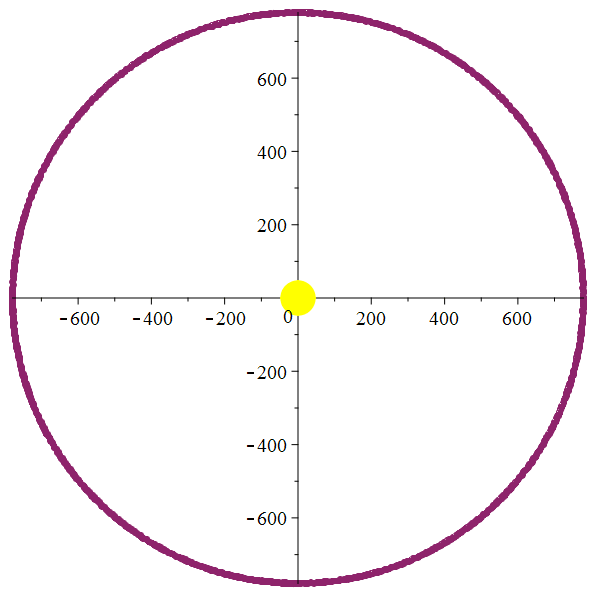
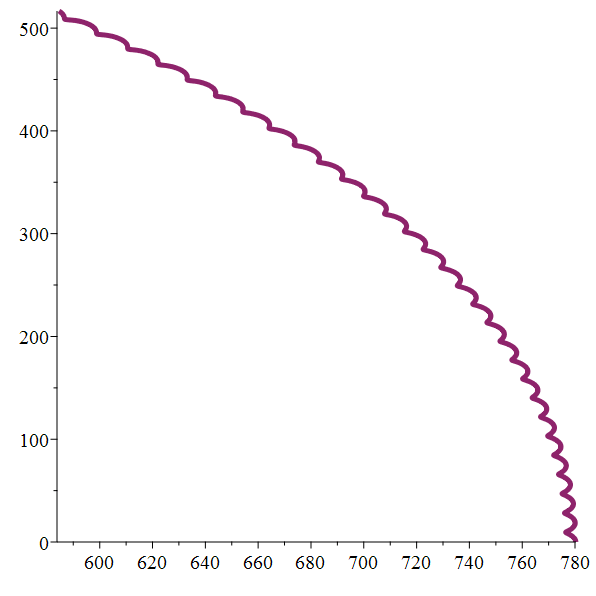
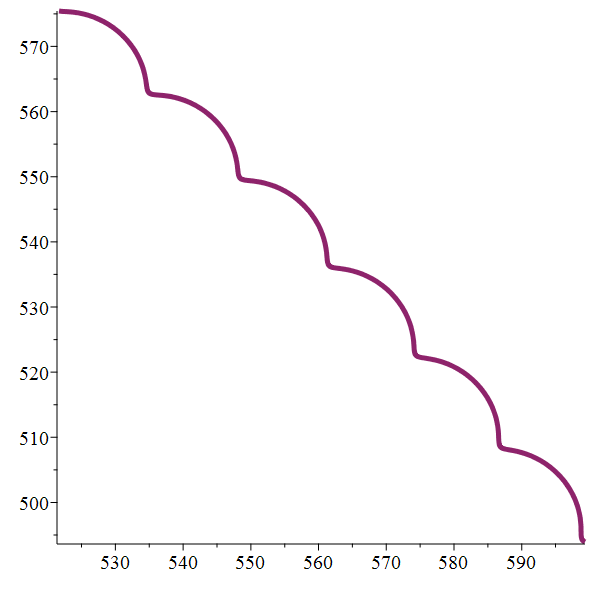
Zoom
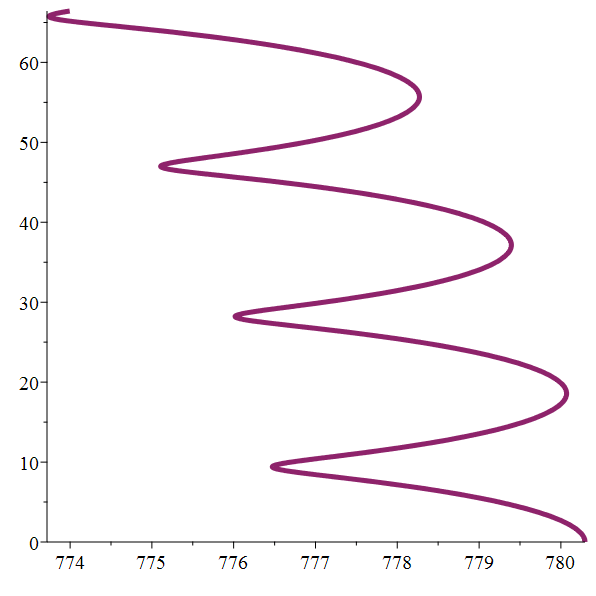
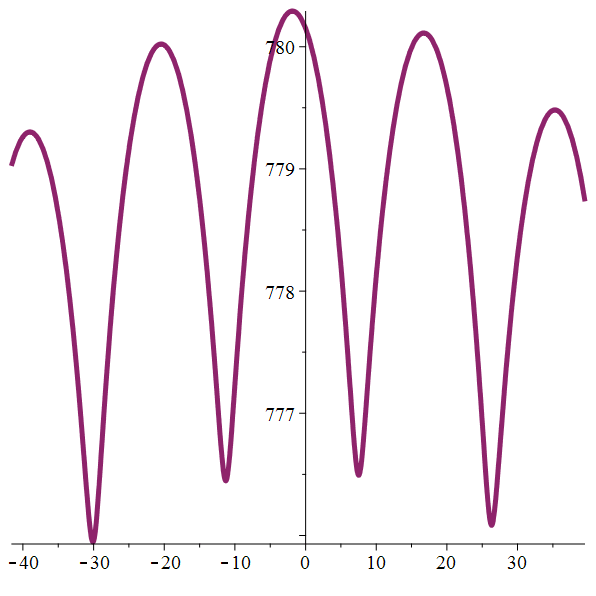
Méga-zoom
Un satellite de Saturne

Saturne et Titan
| Planète | rayon orbital | période
de révolution |
|
| Titan | \(1\,221\,865\) km | \(16\) jours |
Orbite héliocentrique de Titan
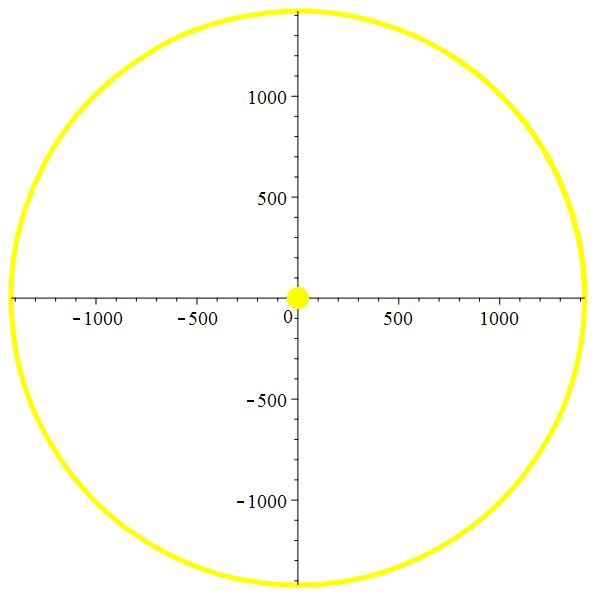
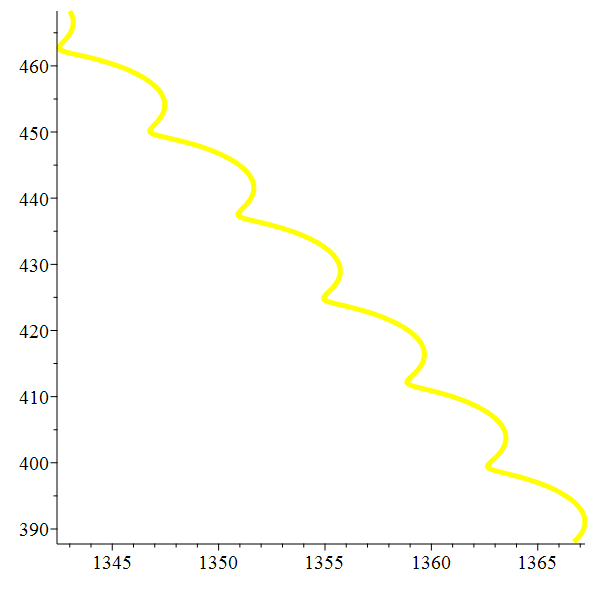
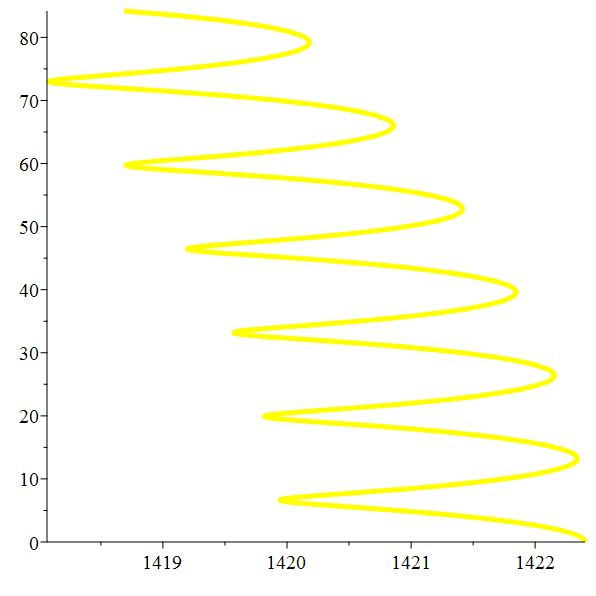
Zoom
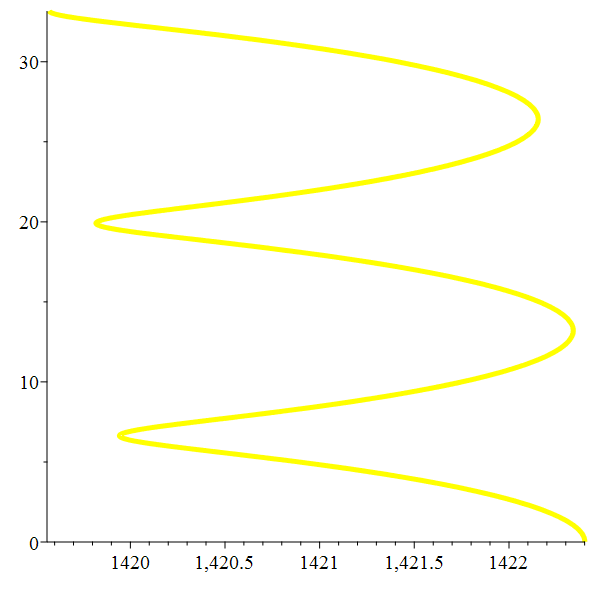
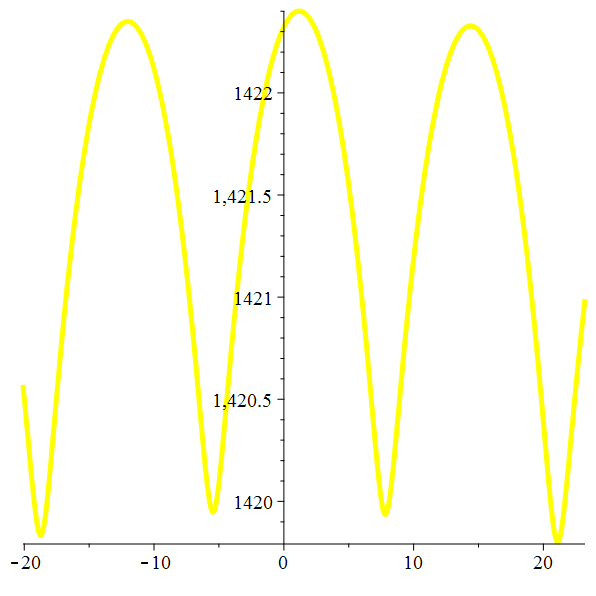
Méga-zoom
–––––––––
Petite remarque en passant :
 |
en fait les orbites planétaires
ne sont pas vraiment circulaires
mais plutôt elliptiques… ou pas !
|
 |
Lois de Kepler/Newton pour deux corps
et problème des trois corps ou plus
 |
| Isaac Newton |
| (1642–1727) |
Physicien, mathématicien,
philosophe, alchimiste,
astronome et théologien anglais
|
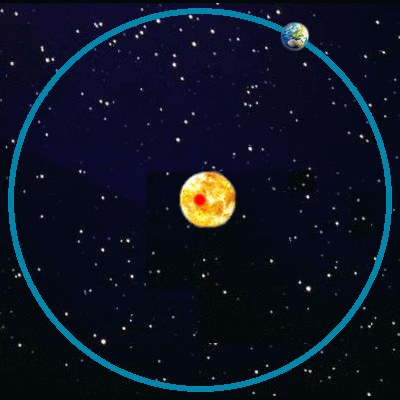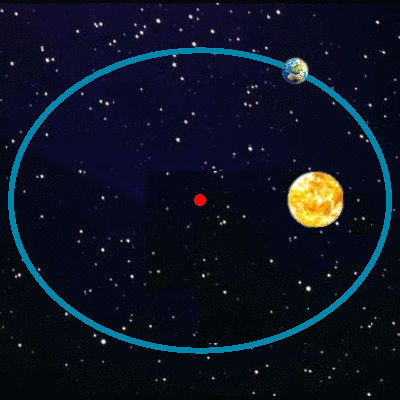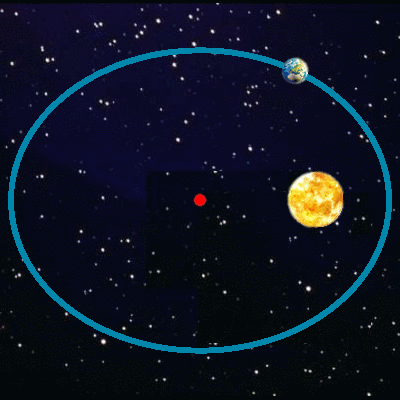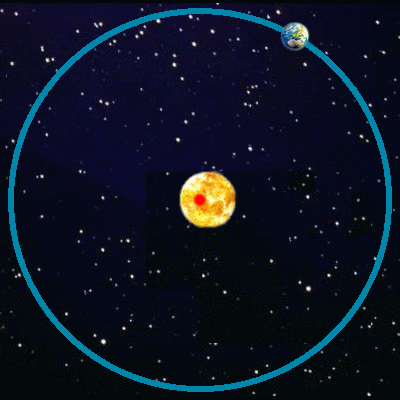
Orbite quasi circulaire
à elliptique
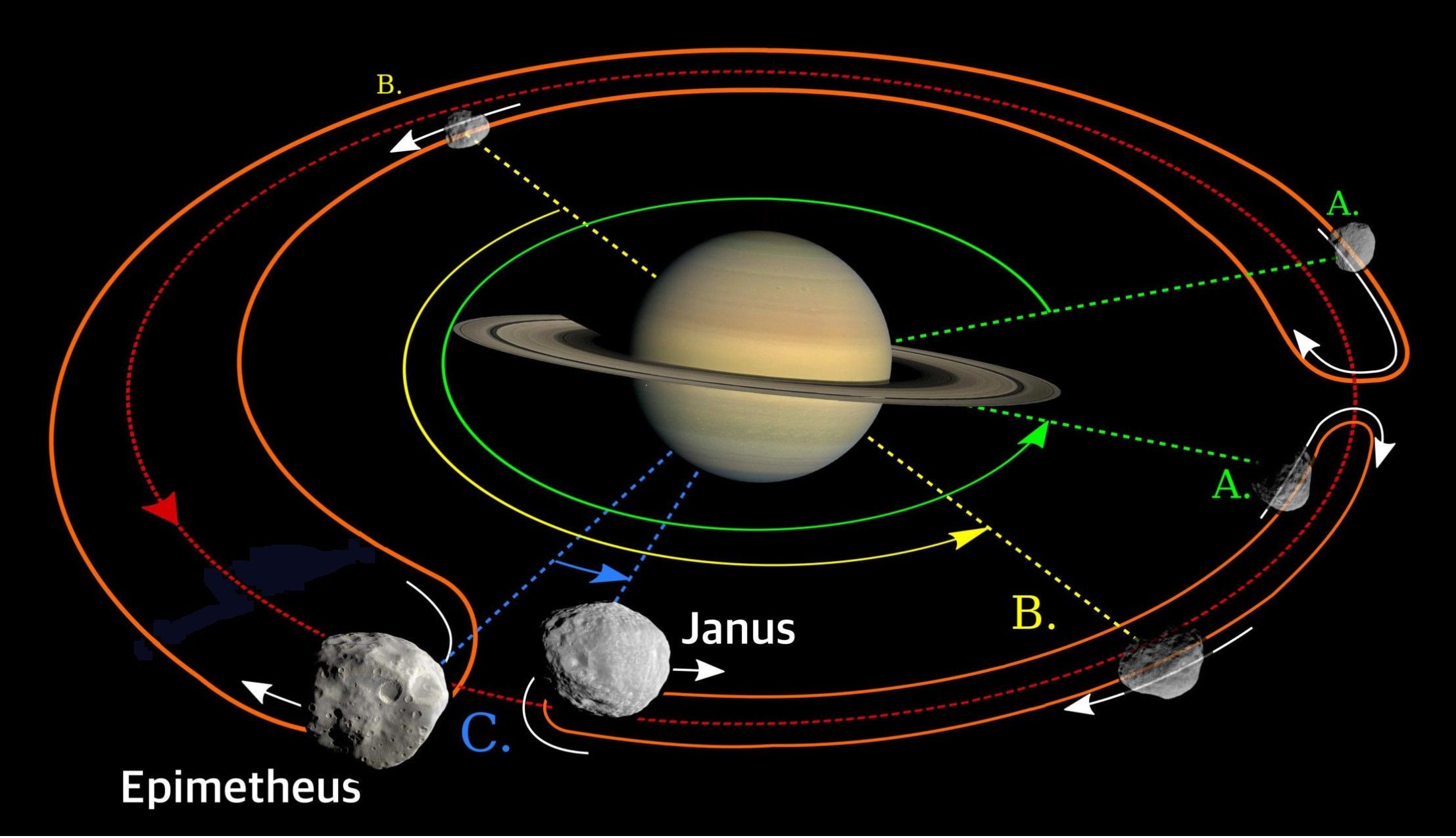
Orbites synchronisées…
ou chaotiques…
\(\vphantom{a_q}\)Un peu de géométrie :
du côté des fractales…
Des récurrences simples mais complexes…
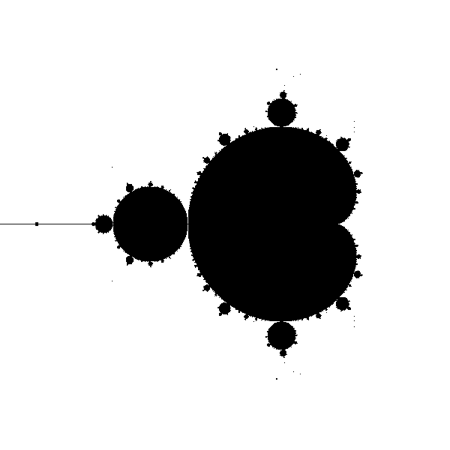 |
| \(z_{n+1} = z_n^2 + c\quad\) (\(z_0 = 0\)) |
Ensemble de Mandelbrot :
ensemble des points \(c\in\mathbb{C}\) pour lesquels
la suite \((z_n)_{n\in\mathbb{N}}\) est bornée |
| |
 |
 |
|
 |
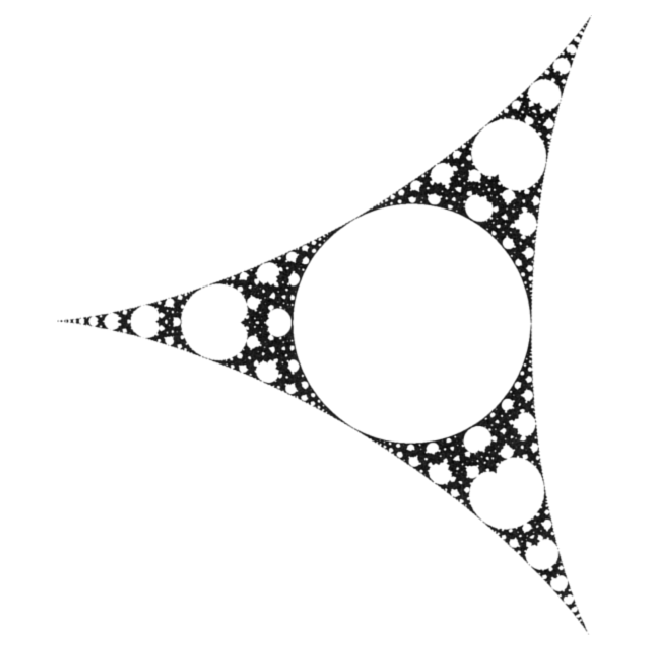
| \(z_{n+1} = z_n^3 + c\quad\) (\(z_0 = 0\)) |
|
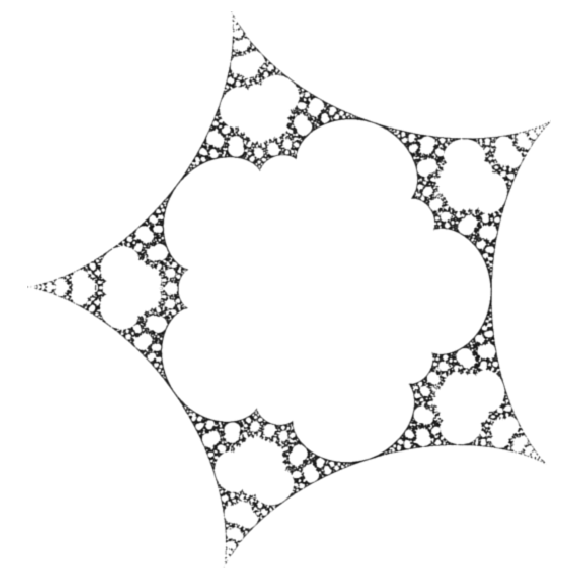
\(z_{n+1} = z_n^4 + c\quad\) (\(z_0 = 0\)) |
 |
|
 |
| \(z_{n+1} = z_n^{-2} + c\quad\) (\(z_0 = 0\)) |
|
\(z_{n+1} = z_n^{-4} + c\quad\) (\(z_0 = 0\)) |
Mandelbrot et multibrots…

animation 
Un peu d'horlogerie : \(\vphantom{a_q}\)avec le temps…

animation 

stop 
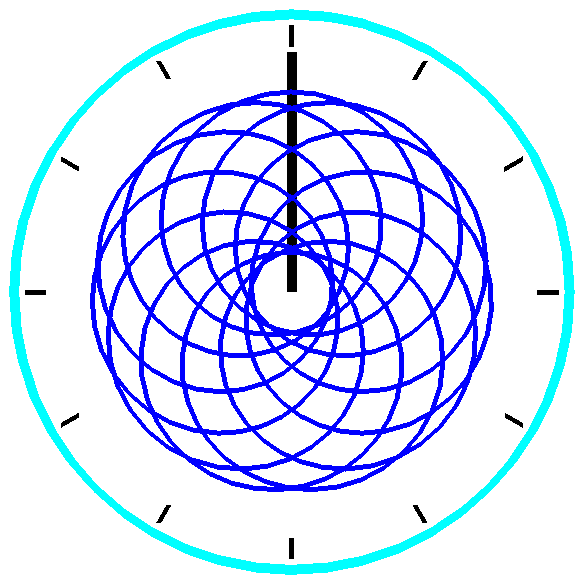
Entre deux aiguilles :
une épitrochoïde allongée…
Le milieu des extrémités des deux aiguilles
décrit une épitrochoïde allongée !
\(\vphantom{a_q}\)Dans mon garage…

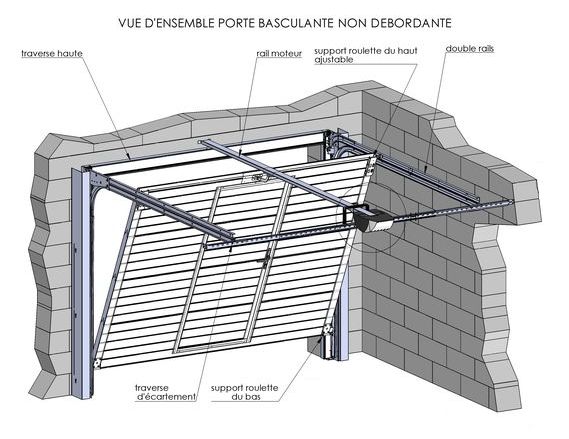
Une porte basculante
non débordante
animation