-

Aimé Lachal Suites récurrentes Cas croissant
| \(\color{blue}\;f(x)\!=\!\sqrt{x+1}\;\) | \(\;u_0\!=\!1.2\;\) |
| \(\color{blue}\ell\!=\!\frac{1}{2}\!\big(1\!+\!\sqrt5\big)\approx 1.618\) | |
| \(\color{blue}\begin{array}{l}f'(\ell)\!=\!\frac{1}{4}\!\big(\sqrt5\!-\!1\big)\approx 0.309 \\ |f'(\ell)|\!<1\end{array}\) |
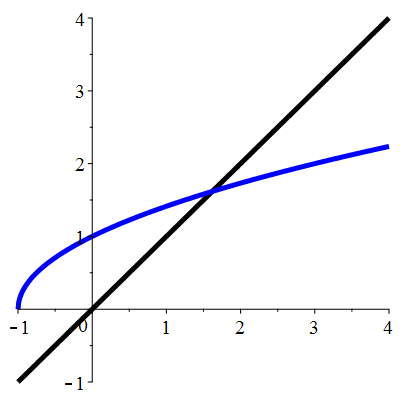
Aperçu global
| \(\color{blue}\;f(x)\!=\!\sqrt{x\!+\!1}\;\) | \(\;u_0\!=\!2\;\) |
| \(\color{red}\;g(x)\!=\!x^2-1\;\) | \(\;u_0\!=\!1.63\;\) |
| \(\color{red}\begin{array}{l}\ell_1\!=\!\frac{1}{2}\!\big(1\!-\!\sqrt{5}\big)\approx -0.618 \\ \ell_2\!=\!\frac{1}{2}\!\big(1\!+\!\sqrt{5}\big)\approx 1.618\end{array}\) | |
| \(\color{red}\begin{array}{l} g'(\ell_1)\!=\!1\!-\!\sqrt{5}\approx-1.236 \\ g'(\ell_2)\!=\!1\!+\!\sqrt{5}\approx3.236 \\ |g'(\ell_1)|>1\qquad |g'(\ell_2)|>1\end{array}\) |
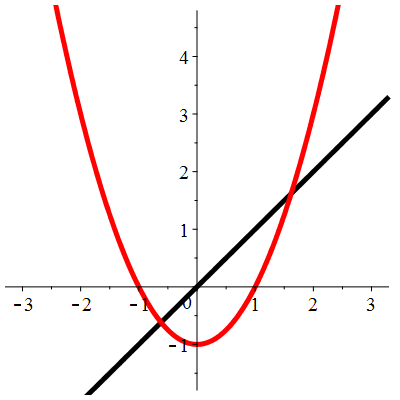
Aperçu global
| ◄ | Sommaire | ► |