Cas décroissant

Aimé Lachal Suites récurrentes Cas décroissant

III. Cas décroissant

Exemple 3

\(\color{blue}\;f(x)\!=\!\frac12\!\big(3\!-\!\sqrt{8x\!+\!1}\big)\;\) \(\;u_0\!=\!0.1\;\)

Point fixe : \(\color{blue}\ell\!=\!\frac{1}{2}\!\big(5\!-\!\sqrt{17}\big)\approx 0.438\)

Dérivée au point fixe : \(\color{blue}\begin{array}{l}f'(\ell)\!=\!\!-\!\frac{2}{13}\!\big(2\!+\!\sqrt{17}\big)\approx-0.942 \\ |f'(\ell)|\!<1\end{array}\)

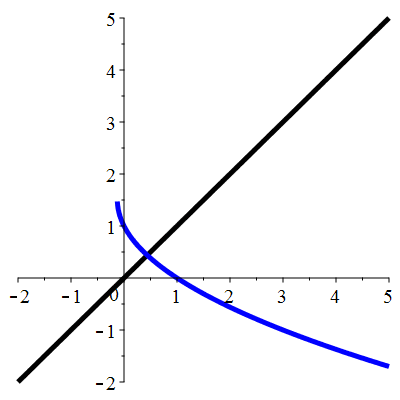
Aperçu global

animation

stop

\(u_0 < u_2 < u_3 < u_1\)

Les suites \((u_{2n})_{n\in\mathbb{N}}\) et \((u_{2n+1})_{n\in\mathbb{N}}\)
sont croissante et décroissante
et convergent vers \((5\!-\!\sqrt{17})/2\)

Exemple 4a

\(\;\color{red}g(x)\!=\!\frac12\!\big(x^2\!-\!3x\!+\!2\big)\;\) \(\;u_0\!=\!\!-0.1\;\)

Points fixes : \(\begin{array}{l}\ell_1\!=\!\frac{1}{2}\!\big(5\!-\!\sqrt{17}\big)\approx 0.438 \\ \ell_2\!=\!\frac{1}{2}\!\big(5\!+\!\sqrt{17}\big)\approx 4.561\end{array}\)

Dérivée aux points fixes : \(\color{red}\begin{array}{l}g'(\ell_1)\!=\!\frac{1}{2}\!\big(2\!-\!\sqrt{17}\big)\approx-1.061 \\ g'(\ell_2)\!=\!\frac{1}{2}\!\big(2\!+\!\sqrt{17}\big)\approx3.061 \\ |g'(\ell_1)|>1\qquad |g'(\ell_2)|>1\end{array}\)

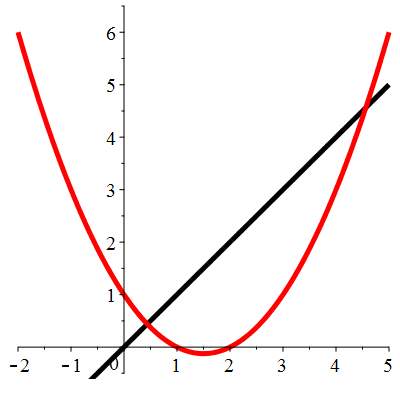
Aperçu global

animation

stop

\(u_0 < u_2 < 0 < 1 < u_3 < u_1\)

La suite \((u_{2n})_{n\in\mathbb{N}}\) est croissante
et converge vers 0
La suite \((u_{2n+1})_{n\in\mathbb{N}}\) est décroissante
et converge vers 1

La suite \((u_n)_{n\in\mathbb{N}}\) est divergente

Exemple 4b

\(\;\color{red}g(x)\!=\!\frac12\!\big(x^2\!-\!3x\!+\!2\big)\;\) \(\;u_0\!=\!0.1\;\)

animation

stop

\(0 < u_2 < u_0 < u_1 < u_3 < 1\)

La suite \((u_{2n})_{n\in\mathbb{N}}\) est décroissante
et converge vers 0
La suite \((u_{2n+1})_{n\in\mathbb{N}}\) est croissante
et converge vers 1

La suite \((u_n)_{n\in\mathbb{N}}\) est divergente

–––––––––

Comparaison des fonctions \(\color{blue}f\) et \(\color{red}g :\)

\(\;\color{blue}f(x)\!=\!\frac12\!\big(3\!-\!\sqrt{8x\!+\!1}\big)\;\)

\(\;\color{red}g(x)\!=\!\frac12\!\big(x^2\!-\!3x\!+\!2\big)\;\)

\(\;\color{cyan}(f\!\circ\!f)(x)\!=\!\frac12\!\Big(3\!-\!\sqrt{13\!-\!4\sqrt{8x\!+\!1}}\Big)\;\)

\(\;\color{orange}(g\!\circ\!g)(x)\!=\!\frac18x^4\!-\!\frac34x^3\!+\!\frac78x^2\!+\!\frac34x\;\)

\({\color{blue}f(0)\!=\!1}\;\textbf{et}\; {\color{blue}f(1)\!=\!0}\) donc \(0\) et \(1\) sont des points fixes de \(\color{cyan}f\!\boldsymbol{\circ}\! f\)
\({\color{red}g(0)\!=\!1}\;\textbf{et}\;{\color{red}g(1)\!=\!0}\) donc \(0\) et \(1\) sont des points fixes de \(\color{orange}g\!\boldsymbol{\circ}\! g\)

Points fixes de \(\color{cyan}f\!\boldsymbol{\circ}\! f\) : \(\color{cyan}0,1,\frac{1}{2}\!\big(5\!+\!\sqrt{17}\big)\)

Points fixes de \(\color{orange}g\!\boldsymbol{\circ}\! g\) : \(\color{orange}0,1,\frac{1}{2}\!\big(5\!-\!\sqrt{17}\big),\frac{1}{2}\!\big(5\!+\!\sqrt{17}\big)\)

\(\quad\)–– \(f\)

\(\quad\)–– \(g\)

\(\quad\)–– \(f\boldsymbol{\circ} f\)

\(\quad\)–– \(g\boldsymbol{\circ} g\)

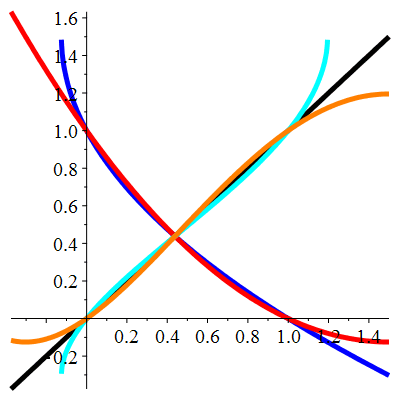
En fait :

\(\begin{cases}\vphantom{\dfrac{b}{a}} ({\color{blue}f}\!\circ\!{\color{red}g})(x)\!=\!x & \text{si }x\!\in\!\mathopen]-\infty,\frac32] \\ ({\color{red}g}\!\circ\!{\color{blue}f})(x)\!=\!x & \text{si }x\!\in\![-\frac18,+\infty[ \end{cases}\)

\({\color{blue}f}\!:\![-\frac18,+\infty\mathclose[\longrightarrow\mathopen]-\infty,\frac32]\)
et
\({\color{red}g}\!:\!\mathopen]-\infty,\frac32]\longrightarrow[-\frac18,+\infty[\)
sont réciproques l'une de l'autre...

◄ Sommaire ►

Point fixe :	\(\color{blue}\ell\!=\!\frac{1}{2}\!\big(5\!-\!\sqrt{17}\big)\approx 0.438\)
Dérivée au point fixe :	\(\color{blue}\begin{array}{l}f'(\ell)\!=\!\!-\!\frac{2}{13}\!\big(2\!+\!\sqrt{17}\big)\approx-0.942 \\ \|f'(\ell)\|\!<1\end{array}\)

Points fixes :	\(\begin{array}{l}\ell_1\!=\!\frac{1}{2}\!\big(5\!-\!\sqrt{17}\big)\approx 0.438 \\ \ell_2\!=\!\frac{1}{2}\!\big(5\!+\!\sqrt{17}\big)\approx 4.561\end{array}\)
Dérivée aux points fixes :	\(\color{red}\begin{array}{l}g'(\ell_1)\!=\!\frac{1}{2}\!\big(2\!-\!\sqrt{17}\big)\approx-1.061 \\ g'(\ell_2)\!=\!\frac{1}{2}\!\big(2\!+\!\sqrt{17}\big)\approx3.061 \\ \|g'(\ell_1)\|>1\qquad \|g'(\ell_2)\|>1\end{array}\)

Points fixes de \(\color{cyan}f\!\boldsymbol{\circ}\! f\) :	\(\color{cyan}0,1,\frac{1}{2}\!\big(5\!+\!\sqrt{17}\big)\)
Points fixes de \(\color{orange}g\!\boldsymbol{\circ}\! g\) :	\(\color{orange}0,1,\frac{1}{2}\!\big(5\!-\!\sqrt{17}\big),\frac{1}{2}\!\big(5\!+\!\sqrt{17}\big)\)