| IV. Autres cas : suites homographiques |
Exemple 5a
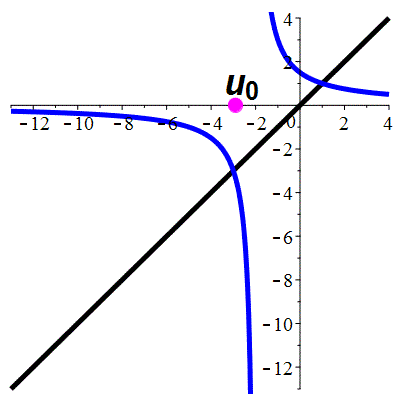
| \(\;\color{blue}f(x)\!=\!\dfrac{\lower 2ex 3}{x\!+\!2}\;\) |
\(\;u_0\!=\!\!-2.9\;\) |
| Points fixes : |
\(\color{blue}\ell_1\!=\!1\) |
\(\color{blue}\ell_2\!=\!\!-3\) |
| Dérivée aux points fixes : |
\(\color{blue}\begin{array}{l} f'(\ell_1)\!=\!\!-\frac13\approx-0.333
\\
|f'(\ell_1)|\!<1\end{array}\)
|
\(\color{blue}\begin{array}{l} f'(\ell_2)\!=\!\!-3
\\
|f'(\ell_2)|\!>1\end{array}\)
|
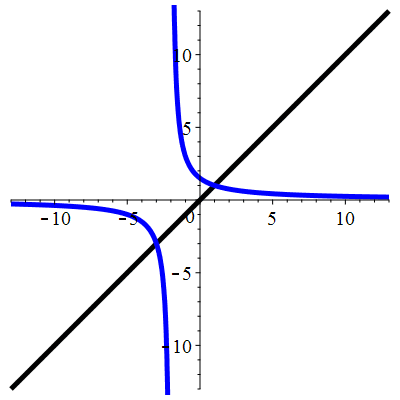
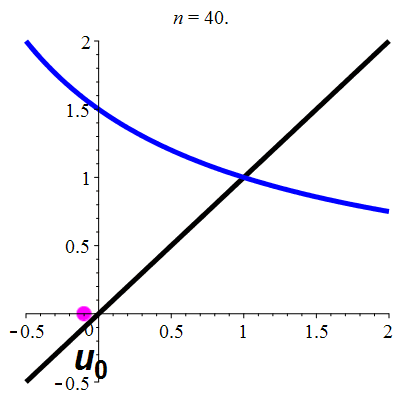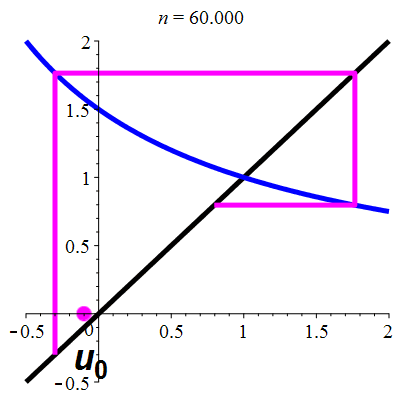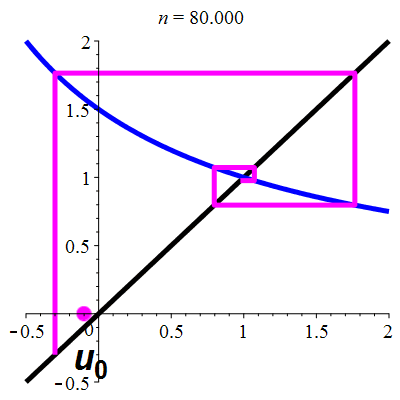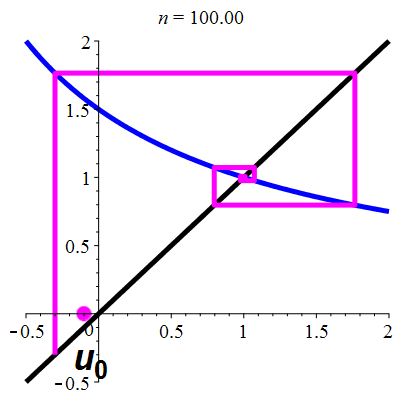
Aperçu global
animation 
Zoom
animation 
stop 
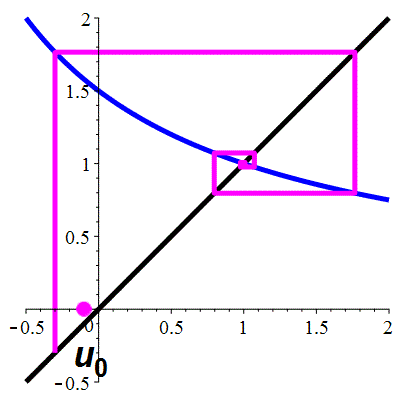
La suite \((u_n)_{n\in\mathbb{N}}\) converge vers 1
Exemple 5b
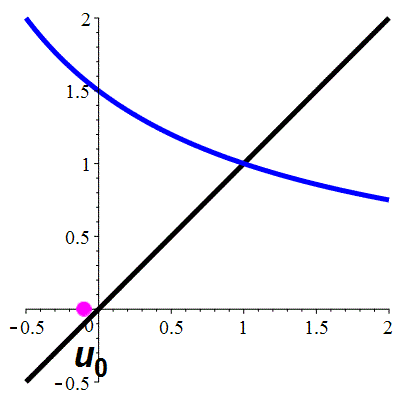
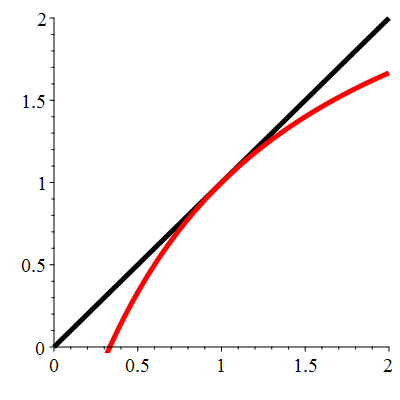
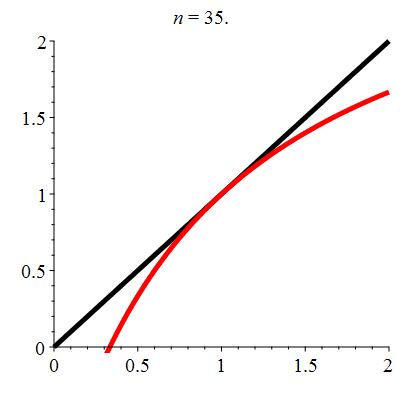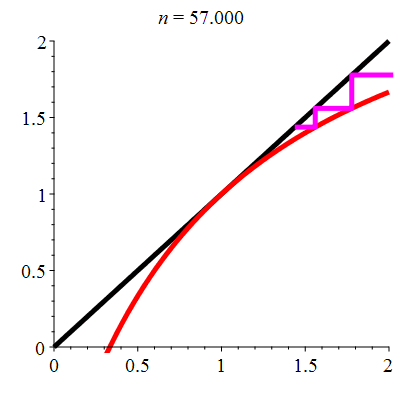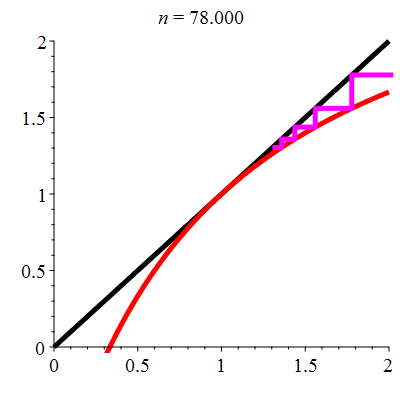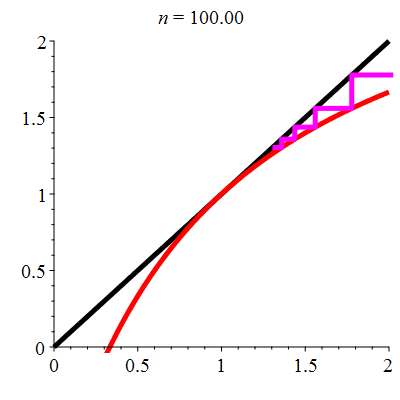
| \(\;\color{red}g(x)\!=\!\dfrac{\lower 2ex {3x\!-\!1}}{x\!+\!1}\;\) |
\(\;u_0\!=\!\!-0.4\;\) |
| Point fixe :
| \(\color{red}\ell\!=\!1\) |
| Dérivée au point fixe : |
\(\color{red}g'(\ell)\!=\!1\) |
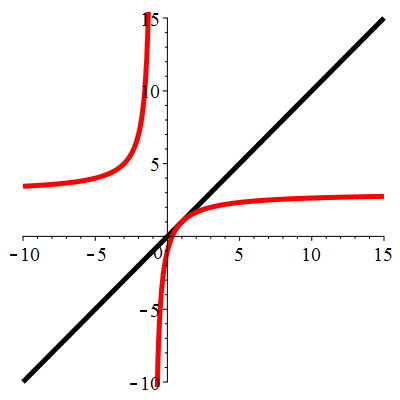
Aperçu global
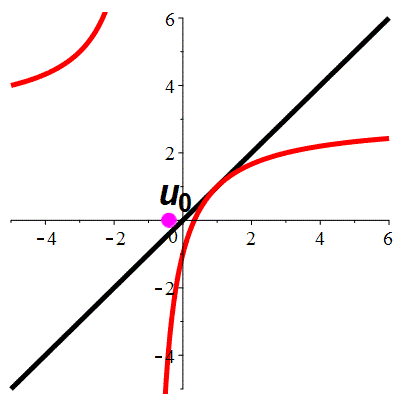
animation 
Zoom
animation 
stop 
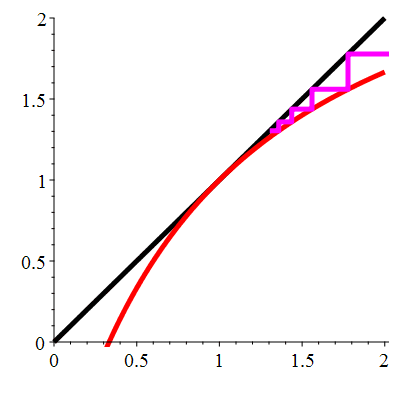
La suite \((u_n)_{n\in\mathbb{N}}\) converge vers 1
Exemple 5c
| \(\;\color{lime}h(x)\!=\!\dfrac{\lower 2ex {2x\!-\!1}}{x\!+\!2}\;\) |
\(\;u_0\!=\!2\;\) |
| Points fixes : |
\(\color{lime}\ell_1\!=\mathrm{i}\) |
\(\color{lime}\ell_2\!=\!-\mathrm{i}\) |
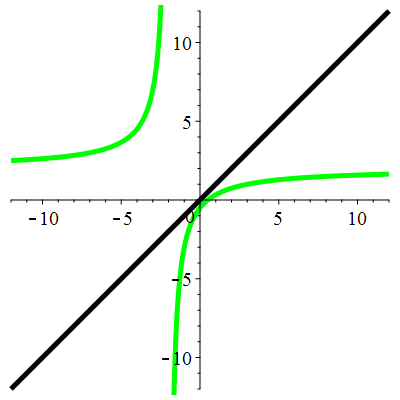
Aperçu global
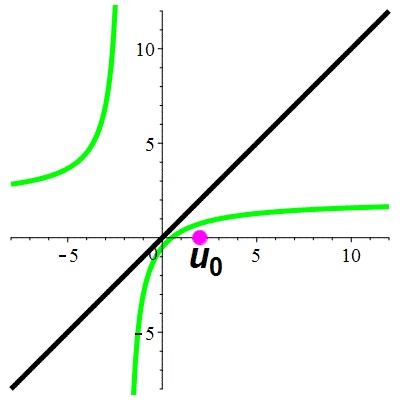
animation 
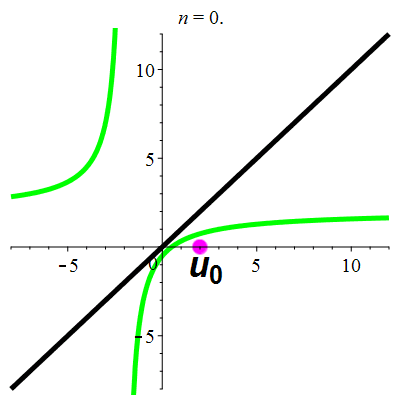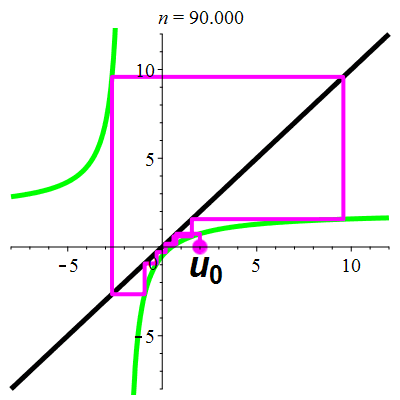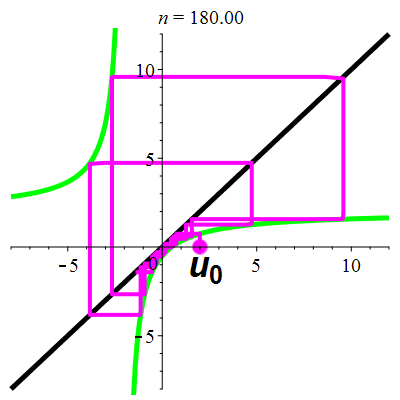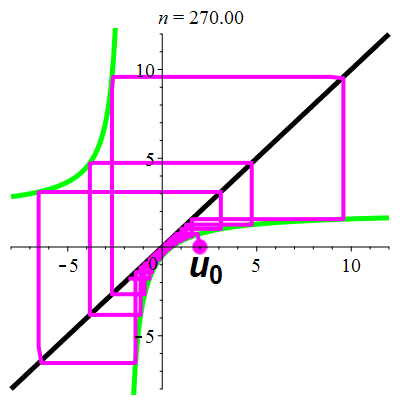
stop 
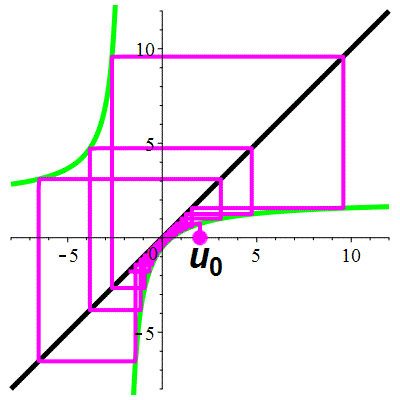
La suite \((u_n)_{n\in\mathbb{N}}\) est divergente
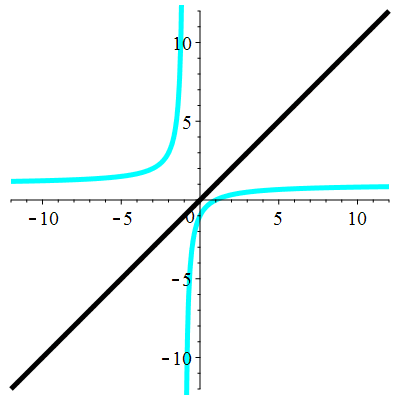
Exemple 5d
| \(\;\color{cyan}k(x)\!=\!\dfrac{\lower 2ex {x\!-\!1}}{x\!+\!1}\;\) |
\(\;u_0\!=\!5\;\) |
| Points fixes : |
\(\color{cyan}\ell_1\!=\mathrm{i}\) |
\(\color{cyan}\ell_2\!=\!-\mathrm{i}\) |
Aperçu global
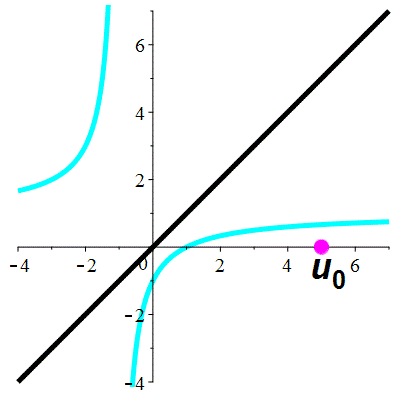
animation 
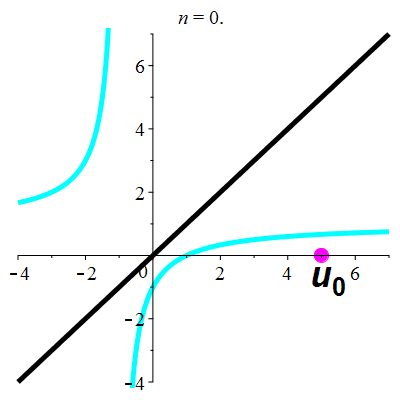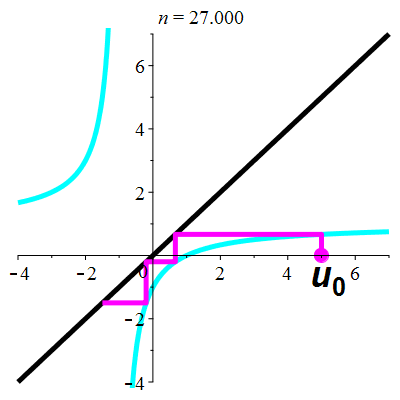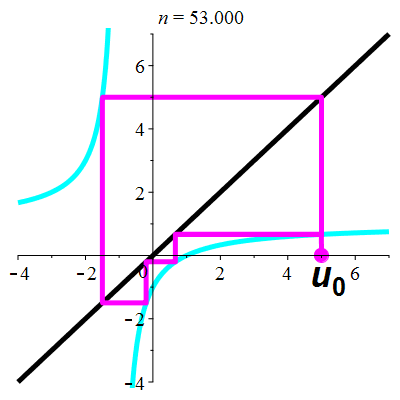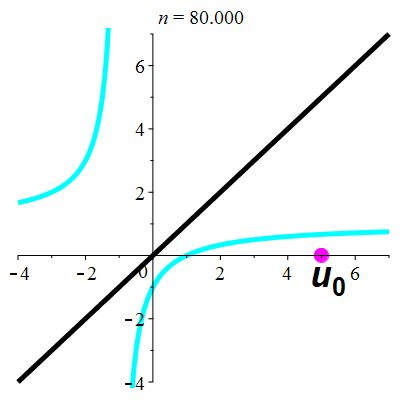
stop 
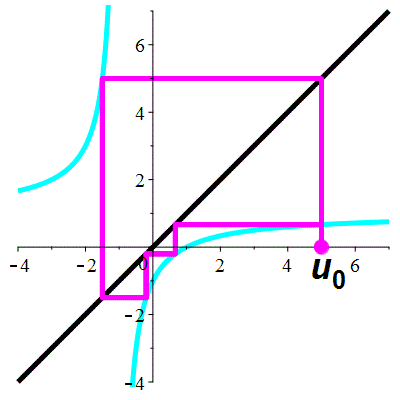
La suite \((u_n)_{n\in\mathbb{N}}\) est divergente
et périodique
Cas général
Soit \(a,b,c,d\in\mathbb{R}\) tels que \(c\neq0\) et \(ad-bc\neq 0.\)
| \(\;f(x)\!=\!\dfrac{\lower 1ex {ax+b}}{cx+d}\;\) |
\(\;u_0\!\in\!\mathbb{R}\;\) |
La suite \((u_n)_{n\in\mathbb{N}}\) est bien définie si et seulement si
\(u_0\neq -\dfrac{d}{c}\) ainsi que toutes ses images successives par \(f :\)
\(u_0,f(u_0),f(f(u_0)),f(f(f(u_0))),\dots\neq-\dfrac{d}{c}.\)
Considérons l'équation aux points fixes \((E)\) de \(f :\)
\[\begin{array}{rl}f(r)=r&\Longleftrightarrow\dfrac{ar+b}{cr+d}=r\\
&\Longleftrightarrow (E) : \;cr^2+(d-a)r-b=0\end{array}\]
On suppose que \(u_0\) n'est pas un point fixe de \(f :\)
(sinon la suite est constante).
1er cas : \((E)\) admet deux racines distinctes
(réelles ou complexes) \(r_1\) et \(r_2.\)
Introduisons \(v_n=\dfrac{u_n\!-\!r_1}{u_n\!-\!r_2}.\) On peut voir en posant \(\rho=\dfrac{a\!-\!r_1c}{a\!-\!r_2c}\) que
\[\forall n\!\in\!\mathbb{N},\;v_{n+1}=\rho v_n.\]
(Notons que l'hypothèse \(ad-bc\neq0\) entraîne que \(a/c\) n'est pas un point fixe de \(f\)
et que \(\rho\) est bien défini, non nul et distinct de 1.)
Ainsi, \((v_n)_{n\in\mathbb{N}}\) est une suite géométrique
(éventuellement complexe) de raison \(\rho.\)
Donc \(\forall n\!\in\!\mathbb{N},\;v_n=v_0\rho^n\) avec \(v_0=\dfrac{u_0\!-\!r_1}{u_0\!-\!r_2}\) d'où l'on tire
\(u_n=\dfrac{r_2v_n\!-\!r_1}{v_n\!-\!1},\) soit :
|
\(\forall n\!\in\!\mathbb{N},\;u_n=\dfrac{r_2v_0\rho^n\!-\!r_1}{v_0\rho^n\!-\!1}\)
|
- Si \(|\rho|<1,\) la suite \((u_n)_{n\in\mathbb{N}}\) converge vers \(r_1;\)
- Si \(|\rho|>1,\) la suite \((u_n)_{n\in\mathbb{N}}\) converge vers \(r_2;\)
- Si \(|\rho|=1,\) la suite \((u_n)_{n\in\mathbb{N}}\) est divergente.
Dans ce cas \(\rho\) est de la forme \(\mathrm{e}^{\mathrm{i}\theta}\).
Lorsque \(\theta\) est un multiple rationnel de \(\pi,\) la suite est périodique.
Tel est le cas lorsque \(\rho=-1,\) ou de manière équivalente, \(a+d=0.\)
2e cas : \((E)\) admet une racine double \(r\) (\(r=\frac{a-d}{2c}\)).
Introduisons \(v_n=\dfrac{1}{u_n\!-\!r}.\) On peut voir en posant \(\rho=\dfrac{2c}{a\!+\!d}\) que
\[\forall n\!\in\!\mathbb{N},\;v_{n+1}=v_n+\rho.\]
(Notons que les hypothèses \(c\neq0\) et \(ad-bc\neq0\) entraînent que \(a+d\neq0\)
et que \(\rho\) est bien défini et non nul.)
Ainsi, \((v_n)_{n\in\mathbb{N}}\) est une suite arithmétique de raison \(\rho.\)
Donc \(\forall n\!\in\!\mathbb{N},\;v_n=\rho n+v_0\) avec \(v_0=\dfrac{1}{u_0\!-\!r}\) d'où l'on tire
\(u_n=\dfrac{1}{v_n}\!+r,\) soit :
|
\(\forall n\!\in\!\mathbb{N},\;u_n=\dfrac{r\rho n\!+\!rv_0\!+\!1}{\rho n\!+\!v_0}\)
|
La suite \((u_n)_{n\in\mathbb{N}}\) converge vers \(r.\)



![]()


![]()

