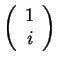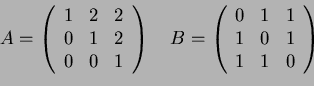suivant: Variables et types de monter: intsci précédent: Table des matières Table des matières

Sous-sections

Prise en main

Dans ce premier chapitre, nous allons passer en revue quelques possibilités basiques de Scilab. Le but est de donner au lecteur, un rapide aperçu de cet environnement.

Début de session

Ouvrons une session Scilab : sous shell unix tapez scilab.

Doit apparaître la fenêtre:

$\includegraphics[clip=false,scale=0.7,angle=0]{PrincipaleWindow.eps}$

avec en dernière ligne, le prompt (->) , qui vous invite à taper une commande.

Une calculatrice scientifique

Répondant à l'invitation du prompt on commence par :

-->2+2

après retour chariot nous obtenons

 ans  =
 
    4.

ce qui nous permet de constater que nous sommes face à une simple calculatrice en ligne, qui évalue l'expression tapée. Les symboles usuels reconnus sont : +, -, * (multiplication), / (division à droite), $\bgroup\color{black}$ \backslash$\egroup$ (division à gauche), ^ ou ** (exponentiation) et les parenthèses ouvrante et fermente.

**Figure 1.1:** Opérations algébriques
$\begin{figure}\begin{center} \begin{tabular}{\vert c\vert l\vert} \hline + & add... ...\\ \^{ } ou ** & exponentiation\\ \hline \end{tabular}\end{center}\end{figure}$

La ``virgule'' des nombres décimaux est remplacée par le ``.'', et Scilab reconnaît la notation scientifique :

-->1.2E-1
 ans  =
 
    0.12

ou similairement

-->1d-4
 ans  =
 
    0.0001

Scilab interprète également la quasi-totalité des fonctions standards telles : sin, cos, tan, exp, log (logarithme népérien) ... Consultez la table de fonctions usuelles.

**Figure 1.2:** Fonctions usuelles
$\begin{figure}\begin{center} \begin{tabular}{\vert c\vert l\vert} \hline abs() &... ...\ tanh()& Tangente hyperbolique\\ \hline \end{tabular}\end{center}\end{figure}$

-->sin(2* %pi +1)^2 / (tan(10.2) +1)
 ans  =
 
    0.4295621

Noter l'usage de %pi (valeur $\bgroup\color{black}$ \pi$\egroup$ ), le % est réservé aux variables pré-définies telles : %i la racine carrée de -1, %e=2.7182818 ou encore %eps=4.441E-16 précision machine... voir la table des variables réservées.

**Figure 1.3:** Quelques variables prédéfinies
$\begin{figure}\begin{center} \begin{tabular}{\vert c\vert l\vert} \hline \texttt... ... \texttt{\%s} &monôme polynômial\\ \hline \end{tabular}\end{center}\end{figure}$

Nombres complexes

La variable %i nous permet de composer avec les complexes

-->(1-%i)^2
 ans  =
 
  - 2.i

Les fonctions usuelles sont étendues aux valeurs complexes.

-->sin(1+%i)
 ans  =
 
    1.2984576 + 0.6349639i

De ce fait Scilab traite implicitement les valeurs réelles et complexes.

$\bgroup\color{black}\framebox{\textbf{A faire :}}\egroup$ évaluer

imag(1-%i)
real(1-%i)
abs(1-%i)
atan(1,-1)

Format d'affichage

Scilab est un logiciel de calcul à précision finie (en principe de l'ordre de 16 chiffres significatifs : ``double précision''). Cela fait plus de décimales que les résultats obtenus précédemment. Mais il est possible de fixer ce nombre de décimales à afficher, ainsi que la forme (format scientifique), c'est la commande format qui est d'usage :

-->1/3 , format("v",16); 1/3
 ans  =
 
    0.3333333  
 ans  =
 
    0.3333333333333

ou encore

-->1/3 , format("e"); 1/3
 ans  =
 
    0.3333333  
 ans  =
 
    3.333E-01

format spécifie le type d'affichage (``v'' ou ``e'') et le nombre de caractères du résultats (1 caractère pour le signe). Néanmoins il est possible d'afficher plus de décimales que la précision machine %eps (qui est la plus grande quantité telle que 1=1+%eps), ceci est dépendant en partie de l'unité arithmétique de la machine.

Le mode par défaut est : format('v',10).

Remarque : la virgule et le point virgule séparent les instructions, la virgule autorise l'affichage de l'évaluation de l'expression, mais pas le point virgule (Taper 1/3 puis 1/3;).

Matrices

Étendons un peu plus les capacités de cette super calculatrice, notamment au calcul matriciel pour cela faisons

-->[1 2 ; 3,4]  
 ans  =
 
!   1.    2. !
!   3.    4. !

ce qui rend la composition de matrices aisée, avec une écriture ligne par ligne. Les espaces ou virgule (`` '' ou ``,'') jouent le rôle de ``séparateur'' des colonnes et le ``;'' celui des lignes, le tout englobé dans des crochets ouvrant-fermant [ ]. Pour des raisons pratiques, on peut être amené à écrire la matrice sur plusieurs lignes, alors cette fois c'est le passage à la ligne qui fait office de délimiteur de fin de ligne (de la matrice).

-->[1 2
--> 3,4]  
 ans  =
 
!   1.    2. !
!   3.    4. !

Remarque : La matrice peut être réelle ou complexe exemple :[1+2*%i , %i; 1 2].

La multiplication matricielle devient une simple opération en ligne

-->[1 2 ; 3 4]*[0 1; 1 0]
 ans  =
 
!   2.    1. !
!   4.    3. !

ou encore

-->2*[1 2 ; 3 4]
 ans  =
 
!   2.    4. !
!   6.    8. !

Bien sûr quand cela est possible !

-->[1 ; 2]*[0 1; 1 0]
                   !--error    10 
inconsistent multiplication

mais

-->[0 1; 1 0]*[1 ; 2] 
 ans  =
 
!   2. !
!   1. !

$\bgroup\color{black}\framebox{\textbf{A faire :}}\egroup$ Taper [1 2]+1.

Opérations sur les matrices

Les combinaisons algébriques de matrice engendrent rapidement des opérations admissibles plus nombreuses que le cas scalaire, par exemple la transposition, multiplication terme à terme, multiplication de Kronecker, division à gauche, à droite, terme à terme ... Toutes ces règles demeurant applicables pour le cas scalaire.

Bien sûr les opérations +,- et * fonctionnent (à condition que les tailles soient compatibles).

Faisons un petit tour des opérations matricielles courantes.

La transposition : signe ' (simple quote ou apostrophe)

-->a=[1 2]'
 a  =
 
!   1. !
!   2. !

La multiplication terme à terme : signe .*

-->[1 2].*[2 3]
 ans  =
 
!   2.    6. !

La division terme à terme : signe ./

-->[1 2]./[2 3]
 ans  =
 
!   0.5    0.6666667 !

L'exponentiation : Pour le signe ^ nous avons 2 comportements :

-->[1 2]^2
 ans  =
 
!   1.    4. !

mais

-->[1 2;3 4]^2
 ans  =
 
!   7.     10. !
!   15.    22. !

alors que

-->[1 2;3 4].^2
 ans  =
 
!   1.    4.  !
!   9.    16. !

Autrement dit, si la matrice n'est pas carrée l'exponentiation agit terme à terme, et dans le cas d'une matrice carrée le signe ^ correspond à l'exponentielle de l'opérateur linéaire de la matrice (définie sous forme de série).

Ce dernier exemple illustre l'usage du point (.) devant l'opérateur, cette extension indique que l'opération voulue à lieu élément par élément.

**Figure 1.4:** Opérateurs algébriques matriciels
$\begin{figure}\begin{center} \begin{tabular}{\vert c\vert l\vert} \hline \texttt... ...ponentiation élément par élément\\ \hline \end{tabular}\end{center}\end{figure}$

Finissons notre courte description sur les opérations matricielles en remarquant que les fonctions usuelles (sin, cos, tan ...) s'appliquent à chaque terme de la matrice (ou vecteur!)

-->sin([%pi, %pi/2])
 ans  =
 
!   1.225E-16    1. !

Scilab possède également des fonctions propres aux matrices carrées^1.1 (définition sous forme de série) comme : expm exponentielle matricielle, avec l'extension ``m'' pour les différencier.

**Figure 1.5:** Fonctions usuelles matricielles
$\begin{figure}\begin{center} \begin{tabular}{\vert c\vert l\vert} \hline acoshm(... ...\\ tanm()& Tangente matricielle\\ \hline \end{tabular}\end{center}\end{figure}$

Un environnement matriciel sans opérations d'algèbre linéaire serait sans intérêt. Scilab met à disposition un grand nombre de fonctions telles inv (inverse de matrice), det (déterminant), spec (extraction de valeurs et vecteurs propres), lu (décomposition LU) ...

Booléens

Pour compléter cette première description des capacités calculatoires de Scilab, il faut mentionner le calcul booléen. Pour cela, il existe deux variables booléennes %t (pour ``true'') et %f (pour ``false'') qui peuvent être utilisées avec les conjonctions :

de négation (not)
```
-->~%t
 ans  =
 
  F
```
le ``et'' (and)
```
-->%t & %f           
 ans  =
 
  F
```
le ``ou'' (or)
```
-->%t | %f
 ans  =
 
  T
```

Scilab sait évaluer les expressions de comparaison du type : 1==2, 1<2, 1<=2, 1>2 et 1>=2, le résultat est de type booléen.

Remarque : Il y a une distinction nette entre le ``égale `` d'affectation (=) et celui de la comparaison (==).

$\bgroup\color{black}\framebox{\textbf{A faire :}}\egroup$ Taper

typeof(1==2)
%T
%F
%t|%f&%f

Enfin le calcul booléen s'étend aux expressions matricielles

-->[%t %f 1==2]
 ans  =
 
! T F F !

avec

-->~[%t %f 1==2]
 ans  =
 
! F T T !

mais aussi

-->[1 2 3]==[3 2 1]
 ans  =
 
! F T F !

les opérateurs & et agissent sur des matrices de même taille ou alors sur des opérations de type scalaire fois une matrice

-->%t & [%t %f]
 ans  =
 
! T F !

$\bgroup\color{black}\framebox{\textbf{A faire :}}\egroup$ Taper typeof([%t %f 1==2]), size([%t %f 1==2]).

Miscelaneous

Scilab possède une panoplie quasi complète de types de variables tels les chaînes de caractères, polynômes, fractions rationnelles, fonctions, lists, mlist... De plus l'utilisateur à la possibilité d'en créer de nouvelles (mlist) ainsi que de définir pour ces nouveaux types (ou objets) les opérations usuelles +,-,*,/ ... (surcharge d'opérateur).

Scilab intègre un grand nombre de fonctions de l'algèbre linéaire (déterminant, inverse de matrice, valeurs et vecteurs propres ...) ainsi que des procédures de tri et autre indexation. Pour une description plus complète il faut signaler une grand pan (passé sous silence dans ce manuscrit) dédié au traitement du signal.

Scilab offre également la possibilité de manipuler des fenêtres de dialogue, de configurer des menus... Tout ce qu'il faut pour développer des applications orienté utilisateur.

Une grande force de cet espace de travail est de donner à tout moment la possibilité de stocker ou d'affecter un résultat à une variable^1.2.

-->x=0:0.1:0.8;
 
-->x         
 x  =
 
!   0.    0.1    0.2    0.3    0.4    0.5    0.6    0.7    0.8  !

Scilab possède également une riche bibliothèque de fonctions graphiques 2D et 3D.

-->plot(x,sin(x))

et bien d'autres.

$\bgroup\color{black}\framebox{\textbf{A faire :}}\egroup$ Taper plot(), plot2d(), plot3d().

Pour se rendre compte des capacités offertes par cet environnement cliquer sur $\bgroup\color{black}\framebox{Demos}\egroup$ dans la barre des menus de la fenêtre principale.

$\includegraphics[clip=false,scale=0.8,angle=0]{barmenu.eps}$

Aide

Avant de se lancer dans une description plus complète de l'utilisation de Scilab, finissons cette section par quelques incontournables de tout langage : l'aide en ligne.

Nous avons deux fonctions utiles tout d'abord la fonction help

-->help sin

qui renvoie dans une fenêtre un manuel de la commande.

Ensuite la fonction apropos

-->apropos title

qui renvoie sur la liste des manuels contenant la chaîne de caractère (title dans l'exemple).

Bien sûr, il est vivement conseillé à l'utilisateur de cliquer sur $\bgroup\color{black}\framebox{Help}\egroup$ de la barre des menus pour faire apparaître une fenêtre avec un classement thématique. Un clic dessus retourne le help correspondant.

$\includegraphics[clip=false,scale=0.7,angle=0]{helpmenu.eps}$

Astuces

La pratique intensive nécessite l'usage de quelques ``raccourcis clavier'' :

le première ``astuce'' est l'utilisation des flèches $\framebox{$\uparrow$}$ et $\framebox{$\downarrow$}$ qui permettent de naviguer dans l'historique des commandes déjà exécutées (pour les puriste d'unix il est possible d'utiliser Contrôle-N et Contrôle-P).
la seconde est le rappel d'une commande avec le point d'exclamation suivi des premières lettres de cette commande :
```
-->plot()
-->!p
```
la troisième n'est pas une astuce Scilab mais sous linux on peut faire du copier-coller avec la souris : en cliquant du bouton gauche on sur-ligne la partie à copier, puis dans la fenêtre Scilab on clique sur le bouton du milieu (coller).

Conclusion

En conclusion de ces premiers pas en Scilab, celui-ci se présente comme un logiciel puissant, capable d'évaluer un très grand nombre de fonctions mathématiques. De plus on va voir qu'il peut être utilisé comme un langage de programmation, langage qui sera interprété et non pas compilé comme des langages ``classiques'' (C/C++, fortran ...).

Scilab est un logiciel interactif et en même temps un logiciel de programmation avec son propre langage. Nous allons dans la suite décrire un certain nombre de type pré-définis ainsi que les règles de manipulation.

Exercices

Afficher $\pi$ avec 14 chiffres après la virgule.
Calculer $2,5 \times 10^3 + 5$ .
Écrire le vecteur (1 2 4), obtenir sa transposée.
Écrire le vecteur $\left( \begin{array}{c} 1\\ i \end{array} \right)$
Calculer le module est l'argument de $\frac{1}{2- i}$ .
Entrer les matrices :

$\begin{displaymath} A=\left( \begin{array}{ccc} 1 & 2 & 2\\ 0 & 1 & 2\\ 0 & 0 ... ...}{ccc} 0 & 1 & 1\\ 1 & 0 & 1\\ 1 & 1 & 0 \end{array} \right) \end{displaymath}$
Faire le produit matriciel $A \times B$ , puis multiplier terme à terme et la transposée de .

suivant: Variables et types de monter: intsci précédent: Table des matières Table des matières

2003-10-15