suivant: Graphiques monter: intsci précédent: Variables et types de Table des matières

Sous-sections

Programmation

Au delà du fait d'avoir un interpréteur de commande en ligne, Scilab offre des possibilités étendues de programmation. De par son mode interactif, Scilab devient un langage de programmation interprété (et non pas compilé).

Ce côté interprété peu engendrer des temps d'exécution beaucoup plus long qu'un langage classique, car il faut ajouter au temps d'exécution, le temps d'interprétation des commandes. Mais un peu d'expérience permet de vectoriser^3.1 un grand nombre d'opérations et obtenir des temps raisonnables.

Ce désagrément est contrebalancé par deux avantages non négligeables. Le premier est lié à la syntaxe de Scilab qui permet une écriture efficace, pour des manipulations de tableaux et matrices, de tri et autres commandes intégrées. Cela permet, comparé à d'autre langages, d'économiser et de rendre plus concis ses programmes. Le second est dut au fait que nous sommes en permanence dans un espace de travail en mode interactif. Ce style ``debuggage'', donne accès à toutes les variables, permettant d'en modifier le contenu, tracer des graphiques... Ceci est l'avantage du mode interprété.

Script d'exécution

Un script est un fichier texte (Ascii) contenant une suite d'instructions Scilab, le mot programme est oublié pour laisser la place à des termes tels script principal, script d'exécution... Ce fichier est composé avec votre éditeur favori externe à Scilab, ce sera par exemple Emacs, Xemacs, Nedit ou ConText qui possèdent un mode d'édition spécifique à Scilab. Le choix d'un éditeur n'est pas fondamental, par contre il faudra faire attention de toujours finir le fichier avec un retour chariot sous peine que la dernière ligne ne soit pas interprétée.

Dans la suite on prendra pour convention de nom de fichier, l'extension ``.sce'' pour les scripts^3.2.

Une fois nos instructions enregistrées (dans test.sce par exemple), il nous faut l'exécuter. Pour cela on peut aller dans le menu de la fenêtre principale à $\bgroup\color{black}\framebox{\textrm{File}}\egroup$ puis $\bgroup\color{black}\framebox{\textrm{File operations}}\egroup$ pour voir apparaître

$\includegraphics[clip=false,scale=.7,angle=0]{FileOp.eps}$

Ce qui permet de sélectionner le script de notre choix et de l'exécuter en cliquant sur le bouton $\bgroup\color{black}\framebox{\textrm{Exec}}\egroup$ .

Cette méthode peut être délaissée au profit d'une commande en ligne de la forme

-->exec test.sce

-->exec('test.sce')

Mais attention pour que cela se passe correctement il faut que le fichier soit dans le répertoire courant de Scilab, celui pointé par la variable pwd

-->pwd
 ans  =
 
 /home/clopeau

Si notre fichier n'est pas localisé à cet endroit (commande dir() pour voir les fichiers), on peut changer de répertoire avec la commande chdir()

-->chdir('Scilab')
 ans  =
 
    0.  
 
-->pwd
 ans  =
 
 /home/clopeau/Scilab

Autrement, en dernier recours, il est possible de spécifier le nom complet avec répertoire^3.3du script à exécuter.

Éléments de programmation

En premier lieu, il faut savoir qu'il est possible (voir recommandé) d'insérer des commentaires dans un script. Les commentaires sont délimités sur la gauche par le double slash et vont jusqu'à la fin de ligne.

// Ceci est une ligne complete de commentaire

A=[2 3; 1 2] //on peut mettre des commentaires apres des instructions

Si une instruction ne tient pas sur une ligne on peut utiliser l'opérateur ... pour l'écrire sur plusieurs lignes (cette remarque est valable pour les commandes en ligne), exemple :

a=sin(x+2*%pi)*tan(2*x)/...
  (1+x^2+log(1+x))^(asin(%pi/(1+x)))

Enfin une dernière règle est que chaque instruction se trouve, soit sur une ligne distincte, soit sur la même ligne que d'autres et sera séparée par une virgule ou un point virgule^3.4.

a=1; b=2 , c=3

Les instructions propres à la programmation ne sont pas très nombreuses. Elles ont toutes la propriété d'avoir une structure bloc, c'est à dire un mot clef d'ouverture (if, for ...) et un ``end'' de fermeture. Elle possèdent également la caractéristique d'être exécutable dans l'espace de travail, l'affichage des lignes devenant plus serré dans l'attente de l'instruction ``end'' pour évaluer le bloc. Nous allons donc expliciter ces instructions.

if ... elseif ... else ... end

L'instruction conditionnelle est gérée par les mots clefs : if, elseif, else et finalement end. if et end étant obligatoire ainsi que l'ordre (on peut répéter elseif autant que nécessaire).

if test1        // test1 est un booléen (scalaire)
   instruction1
elseif test2
   instruction2 // on peut sous cette forme mettre plusieurs lignes
else
   instruction3
end

Noter la structure bloc qui permet d'insérer une ou plusieurs ligne entre les mots clefs. On peut utiliser tout ou partie de cette structure

if test1
  instruction1
else 
  instruction2
end

Il existe quelques variantes d'écriture de cette instruction conditionnelle notamment, une écriture ligne sous la forme

-->x=1;
-->if x==2, x=1, elseif x==3, x=1, else x=2, end
 x  =
 
    2.

Noter l'usage des virgules après chaque booléen et avant chaque mot clef elseif, else et end, le point virgule pourrait jouer un rôle tout à fait identique (affichage en moins).

select ... case ... else ...end

Il existe une deuxième forme de choix conditionnel

select atester     // atester contient un expression 
  case  cas1       // si atester vaut cas1 alors
     instruction1
  case  cas2       // si atester vaut cas2 alors 
     instruction2
  else             // autrement
     instruction3
end

Cette structure permet d'écrire dans certain cas des arbres de décision plus agréables comme dans l'exemple ci-dessous

a=round(rand(1,2));
select a
  case [0 0]
    b=1;
  case [0 1]
    b=2;
  else
    b=0
end

Il est possible comme précédemment d'avoir une écriture sur une seule ligne de la forme

-->a=round(rand(1,2));
-->select a, case [0 0],b=1,case [0 1],b=2,else,b=0 ,end

la règle étant de toujours respecter l'articulation de la syntaxe par l'emploie de la virgule (ou point virgule).

for ... end

la boucle for pointe sur un ensemble d'indices

for i=1:50
  // i vaut de 1 a 50
  bloc instructions
end

mais peut également se mettre sous la forme

for i=[2 7 1 4]
  bloc instructions
end

la variable i prenant tour à tour les valeurs 2,7, 1 et 4.

Remarque : La variable i est une variable locale à la boucle !

Il est possible de faire une boucle sur une matrice, dans ce cas le compteur est affecté à chaque colonne

for i=[2 3;1 2]
   i vaut [2;1] puis [3;2]
end

Comme pour le choix conditionnel, il est possible d'écrire la commande sur une seule ligne

-->for i=1:5, disp(i); end

Enfin une autre possibilité d'utilisation de la boucle for est de boucler sur une liste d'éléments.

L'instruction break permet de sortir à tout moment de la boucle.

while ... end

L'instruction while est d'un usage simple sous la forme

while test  //test est un booleen scalaire
  bloc instructions
end

Le ``bloc instructions'' est exécuté tant que test est vrai.

L'instruction break permet de sortir à tout moment de la boucle.

Pour les amoureux de lignes peu espacées et aérées, il est toujours possible de faire contenir une boucle conditionnelle sur une seule ligne.

-->while a<10, a=a+1; end

Fonctions

Une façon usuelle de définir des fonctions est de mettre celles-ci dans un fichier à extension ``.sci''. Le nom de fichier est sans importance^3.5, et plusieurs fonctions peuvent être dans le même fichier.

Néanmoins il est possible de définir ``inline'' une fonction avec la commande deff. Depuis la version 2.6 de Scilab, on peut directement dans un script écrire une fonction avec la même syntaxe comme si celle-ci se trouvait dans un fichier séparé. Elle est ``chargée'' automatiquement.

Syntaxe

la fonction doit commencer par le mot réservé function et finir par endfunction sous la forme

function [out1,out2,...,outN]=nomfonction(in1,in2,...,inP)

   // out1,out2,...,outN sont les variables de sortie
   // in1,in2,...,inP variables d entree
   
   instructions
endfunction

Il faut veiller à ne pas ``écraser'' une fonction Scilab existante, dans ce cas doit apparaître un message signalant une telle éventualité.

-->function out=norm(in)                                   
-->  out=sqrt(sum(in.^2,'r'));
-->endfunction
Warning :redefining function: norm

Dans ce dernier cas la fonction est définie directement dans l'espace de travail, elle est automatiquement ``chargée''.

Charger une fonction

Pour que la fonction soit reconnue et exécutée par Scilab il faut la ''charger''. En effet les fonctions sous Scilab ont un statut de variables, et donc nécessitent d'être initialisées. Le fait qu'une fonction soit une variable permet, de manière naturelle de la passer en paramètre.

Pour cela comme pour l'exécution d'un script, par le menu $\bgroup\color{black}\framebox{File}\egroup$ puis $\bgroup\color{black}\framebox{File opérations}\egroup$ , on peut sélectionner le fichier (.sci) et cliquer sur $\bgroup\color{black}\framebox{getf}\egroup$ .

On peut faire ceci en ligne par la commande getf

-->getf NomFichier.sci

-->getf(`'/nom.complet.du.repertoire/NomFichier.sci')

et les fonctions^3.6 de NomFichier.sci deviennent accessibles.

Remarque : Attention quand on modifie une fonction il faut la ``recharger'' (doit apparaître : Warning :redefining function ).

Appel d'une fonction

Pour exécuter une fonction il suffit de l'appeler en passant les arguments nécessaires

-->mafonction(rand(2,2))

Mais dans le cas où ma fonction est définie comme suit

function [a,b]=mafonction(A)
      .....

l'appel précédent ne renvoie que la valeur de a.

Pour obtenir les deux valeurs escomptées il faut faire un appel sous la forme

-->[p,q]=mafonction(rand(2,2))
 q  =
 
!   0.8782165    0.5608486 !
 p  =
 
!   1.           0. !

Ceci est déjà le cas pour un certain nombre de fonctions Scilabpar exemple

-->[m,k]=max(rand(1:10))
 k  =
 
    9.  
 m  =
 
    0.8782165

où la variable k va contenir le rang du terme maximal.

Scilab offre la possibilité lors d'un appel de fonction de contrôler le nombre de paramètres en entrée et sortie. Il s'agit de la commande argn. Voici un exemple d'une fonction, qui teste le nombre d'argument passé en paramètre et calcul le déterminant de l'argument et sa trace dans le cas où deux variables de sortie sont spécifiées.

function [a,b]=mafonction(A)
  [lhs,rhs]=argn()  
                       // lhs : left hand side
                       // rhs : right hand side
  if rhs==0
     disp('Impossible de faire quelque chose')
     return
  end
  a=det(A);
  if lhs==2
    b=trace(A)
  end
endfunction

argn peut être aussi utilisé sous la forme lhs=argn(1) ou rhs=argn(2). Les fonctions varargin et varargout permettent une gestion plus pointue de la liste des variables d'entrées et de sorties.

Variables globales et locales

Scilab fait la distinction entre les variables locales et globales au sein d'une fonction.

Les variables locales sont les variables définies comme entrantes et sortantes (out1,... in1... de la section Syntaxe), et celles qui sont affectées (déclarées) dans la fonction (hormis celles définies par le mot clef global).

Mais implicitement les variables du script (ou fonction appelante) se retrouvent accessibles dans la fonction appelée (mais non modifiable) à condition qu'il n'y ait pas de variable locale de même nom. Par exemple définissons une fonction qui fait appel à la variable a (dans un fichier : mafonc.sce):

function  [out]=mafonc(in)
    out=a*in
endfunction

puis exécutons

-->getf mafonc.sce

-->mafonc(2)
 !--error     4 
undefined variable : a                       
at line       2 of function mafonc                   called by :  
mafonc(2)

-->a=2
 a  =
 
    2.  
 
-->mafonc(2)
 ans  =
 
    4.

Maintenant définissons une nouvelle fonction qui possède a comme variable locale, et qui appelle mafonc

function  [out]=mafonc2(in)
    a=-2; // variable locale
    out=mafonc(in)
endfunction

et maintenant

-->getf mafonc.sce;
-->getf mafonc2.sce;
-->a=2;
-->mafonc2(2)
 ans  =
 
  - 4.  
 
-->mafonc(2) 
 ans  =
 
    4.

Autrement dit dans mafonc2 la valeur de a est changée, dans ce cas a est une variable locale à la fonction. De ce fait les valeurs précédentes de a sont ``écrasées'' (localement) . A contrario, dans mafonc, a et considéré comme une variable globale (ou persistente).

Il est possible par le mot clef global de définir une variable globale. Cette variable est accessible pour toute fonction qui déclare la variable comme globale, redéfinissons mafonc

function  [out]=mafonc(in)
    global a
    out=a*in
endfunction

et relançons l'exécution

-->getf mafonc.sce;
Warning :redefining function: mafonc

-->global a  
 
-->a=2
 a  =
 
    2.  

-->mafonc(2)
 ans  =
 
    4.  
 
-->mafonc2(2)
 ans  =
 
    4.

Finissons par plusieurs mots clefs pour gérer les variables globales.

isglobal(var) vrai si var est déclarée ``globale''.
clearglobal(var) supprime la variable de la liste des variables globales. un appel sans argument supprime toutes les variables globales.
who('global') renvoie la liste des variables globales (homologue local who('local')).

Mise au point d'un programme

Scilab possède un jeu d'instructions de débuggage (setbpt, delbpt, dispbpt). L'usage n'est pas très conviviale et Scilab n'intègre pas d'éditeur qui permette de placer ou d'enlever à la souris de tels points d'arrêts. Mais on peut, tout simplement, placer une commande pause à tout endroit (même dans une fonction^3.7) pour arrêter l'exécution et se retrouver sous un prompt de la forme

-1->

à ce moment on a accès à toutes les variables locales. Toutes les manipulations mêmes graphiques sont possibles. Il est même envisageable d'exécuter, de cet endroit, un autre script que sera un sous processus du premier ...

La commande return continue l'exécution, sans tenir compte des modifications apportées durant l'arrêt. Les variables sont accessibles en lecture durant le mode pause. Si elles sont modifiées, c'est une copie ``locale'' qui est modifiée. Pour pouvoir continuer avec les valeurs modifiées il faut ``recopier'' les variables par la commande [var1, var2, ...]=resume(var1, var2, ...).

Lorsqu'une exécution ne répond plus, la commande Contrôle-C suspend l'exécution. Elle agit à tout moment comme la fonction pause. Par contre on ne sait pas où l'exécution c'est arrêtée, pour cela il faut utiliser la fonction whereami() ou [ligne,fonc]=where().

Remarque : Le 1 qui apparaît dans le prompt ``-1- $\bgroup\color{black}$ >$\egroup$ '' signifie que nous sommes dans un sous processus. Pour abandonner les processus il faut utiliser la commande abort.

Quand on lance un script (commande exec), apparaît dans l'espace de travail les lignes, une à une exécutées. Cela permet de suivre l'exécution de celui-ci. Par contre l'exécution d'une fonction est, à comparer, silencieuse. la commande mode permet de changer cet état.

En spécifiant

mode(-1) aucune ligne (hors commande disp) n'apparaît. C'est la valeur par défaut lors de l'appel une fonction.
mode(0) c'est la règle d'affichage du point virgule qui s'applique : si une instruction est suivi de ';' alors il n'y a pas d'affichage, par contre en cas de retour à la ligne ou ',', le résultat de la commande est affiché.
mode(1) ou mode(3) valeur par défaut pour la commande exec. Les lignes interprétées sont affichées (avec le résultat quand il n'y a pas de ';').

Il est donc possible de changer le ``mode'' dans une fonction pour avoir un regard sur ce qu'elle fait.

Un peu d'optimisation

Tout programmeur est confronté, à un moment ou un autre, au temps de calcul et donc à l'estimation du coût des algorithmes. Scilab étant en mode interprété, il faut connaître quelques comportements classiques engendrés par ce processus. Deux appels successif de la commande timer() permettent de mesurer le temps écoulé (le premier appel initialise le temps de référence, le second renvoie le temps écoulé).

Pour illustrer, regardons le calcul de la somme cumulée d'un vecteur, initialisons un vecteur x^3.8 :

-->x=rand(1,400000);

puis calculons un temps qui sera de référence^3.9:

-->timer(); y=cumsum(x);T_ref=timer()
 T_ref  =
 
    0.06

Maintenant adoptons plusieurs stratégies pour effectuer le même tâche

-->timer(); z(1)=x(1); ...
-->for i=2:length(x), z(i)=z(i-1)+x(i); end, ...               
-->T1=timer()
 T1  =
 
      2179.82

Impossible^3.10 de croire ce résultat un deuxième appel pour le confirmer

...
-->T1=timer()  
 T1  =
 
    9. 91

cela donne un temps beaucoup plus raisonnable. Mais dans cette deuxième exécution, z n'est pas une variable inconnue^3.11. Elle existe et possède déjà la ``bonne'' taille. Dans la première exécution chaque affectations sur z nécessite une ré-allocation (dynamique) de la variable et engendre un travail exagérément élevé. Pour ce convaincre de l'exactitude des mesures précédentes faire

-->clear z

et recommencer.

Ce mécanisme peut être enrayé par une pré-allocation :

-->clear z
 
-->timer(); z=zeros(x); z(1)=x(1); ...          
-->for i=2:length(x), z(i)=z(i-1)+x(i); end, ...
-->T1=timer()                                   
 T1  =
 
    9.87

Ceci conduit à retenir deux principes :

la ré-allocation de variable est à éviter^3.12.
utiliser au mieux les fonctions vectorisées qui permettent d'éviter ou de limiter l'usage de la boucle^3.13 for.

L'écriture vectorisée engendre rapidement des mécanismes d'extraction ou d'affectation. Il est bon de se poser la question de savoir les règles à observer. Pour cela faisons un petit test. Sont proposées les deux fonctions suivantes qui calculent de deux manières distinctes la somme des éléments d'une matrice :

function out=Scol(A)
    // sommation par extraction de colonnes
    [n,p]=size(A);
    som=zeros(n,1);
    for j=1:p
       som=som+A(:,j);
    end
    out=sum(som)
endfunction

function out=Slign(A)
    // sommation par extraction de lignes
    [n,p]=size(A);
    som=zeros(1,p);
    for i=1:n
       som=som+A(i,:);
    end
    out=sum(som)
endfunction

Après avoir chargé ces fonctions on les exécute pour obtenir le temps d'exécution :

-->getf Scol.sce; getf Slign.sce;

-->A=rand(3000,3000); 
-->timer();Scol(A),timer()
 ans  =
 
    4497372.4  
 ans  =
 
    0.62  
-->timer();Slign(A),timer()                 
 ans  =
 
    4497372.4  
 ans  =
 
    2.98

On retrouve ici un classique des langages possédant des tableaux à double entrées, le mode de stockage détermine une façon optimale d'accéder aux éléments. En l'occurrence Scilab stocke les matrices colonnes par colonnes (comme le fortran) à l'instar du C/C++.

A remarquer, la possibilité de syntaxe différentes comme par exemple

function out=Scol2(A)
    // sommation par extraction de colonnes
    [n,p]=size(A);
    som=zeros(n,1);
    for col=A
       som=som+col;
    end
    out=sum(som)
endfunction

pour donner

-->timer();Scol2(A),timer()
 ans  =
 
    4497372.4  
 ans  =
 
    0.65

Cette écriture est aussi compétitive que Scol.

Le ratio entre les deux modes d'accès est ici de 4.8. Il est faible comparé aux ratios obtenus dans le cas de réaffectation ou de comparaisons avec la boucle for, mais il est clairement non-négligeable.

Il nous faut un outil de ``profiling'' pour détecter les lignes gourmandes. Ceci existe avec les commandes profile, showprofile et plotprofile. Pour cela il faut charger la fonction, que l'on veut examiner, sous un mode ``profile'' par

-->getf('Scol.sci','p');

puis faire un appel de cette fonction et examiner le profile

-->Scol(A);

-->showprofile('Scol')
function out=fun(A)               |1   |0   |0|
                                  |1   |0   |0|
[n, p] = size(A);                 |1   |0   |4|
som = zeros(n, 1);                |1   |0   |4|
for j = 1:p,                      |3000|0.01|0|
  som = som + A(:, j);            |3000|0.62|7|
end                               |1   |0   |0|
out = sum(som);                   |1   |0   |3|
endfunction                       |1   |0   |0|

La première colonne indique le nombre d'exécution de la ligne (depuis le dernier getf( ... ,'p')), la seconde le temps cumulé, et la troisième l'effort d'interprétation. Cette dernière est à interpréter avec modération, ne signifiant pas forcément un sur-coût.

C'est l'outil idéal pour traquer, et faire maigrir le temps d'exécution.

Conclusions diverses

Comme promis, Scilab peut être considéré et utilisé comme un langage de programmation. Il faut rapidement éviter les écueils d'une écriture non-vectorisée. Pour ce qui est de la programmation, il est du ressort de chacun de développer son style. Bien sûr de simples règles comme : commenter largement ses lignes, ou d'utiliser des noms de variables le plus explicite ou usuelle dans leur rôle sont à appliquer (un compteur d'indice est souvent i, j ou k, appeler une matrice i ... a vos risques et périls!).

Pour les personnes se sentant démunies face à leur page blanche, je propose un shéma simple. Il ne faut pas oublié que Scilab est un interpréteur de commande possédant des ressources de traitement ou d'affichage de données remarquable. Il serait dommage de se priver d'une tel manne.

Le modèle proposé pour le développement d'une (petite) application est le suivant : il est basé sur l'ouverture simultané de deux fichiers.

le premier MesFonctions.sci contient l'ensemble des fonctions qui vont être écrites :

// Fichier de fonctions : MesFonctions.sci
//----------------------------------------
function out=premierefonc(in)
   ....
endfunction

function out=deusiemefonc(in)
   ....
endfunction
    .
    .
    .

Le second fichier main.sce est le fichier qui sera exécuté, en premier. Il est possible (voir recommander) de compiler les fonction par la fonction getf

// Ceci est le scrip principal
//----------------------------

getf MesFonctions.sci //a partir de la les fonctions sont chargées

// maintenant on peut faire ce que l'on a à faire
...
plot2d(sol,u)
...

Ainsi pour lancer le programme il suffit de lancer la commande

-->exec main.sce

et automatiquement les dernières modifications (même dans le fichier de fonctions) sont prises en compte. De plus une fois le script exécuté, restent les variables disponibles pour être consultées ou affichées. Au programmeur de prendre ses dispositions pour avoir la possibilité à cet endroit, de post-traiter ces résultats.

Une habitude nouvelle, à comparer avec d'autre langages, et de pouvoir tester la syntaxe immédiatement. Supposons qu'une malencontreuse erreur de syntaxe se soit glisser dans une fonction, générant immanquablement une erreur à l'exécution. Immédiatement informé de la ligne correspondante, le programmeur insère un pause ou setbpt avant de relancer l'exécution pour se retrouver en mode ``pause'' avant d'avoir commis la faute. A ce moment là, il est recommander de tester diverses syntaxes et de regarder explicitement les variables concernée par la ligne fautive.

Sur ces dernières recommandations, il peut être sage de faire les quelques exercices proposés dans la section suivante.

Exercices

Les premiers exercices portent sur des mécanismes standards de phénomènes d'erreurs d'arrondi. Cette setion ne fait intervenir que des algorithmes basics, néanmoins les mécanismes mis en avant doivent être en tête pour toute personne voulant faire du calcul numérique à précision finie! (impérativement à connaître).

Exercice I : Somme d'une suite alternée.

Le développement en série entière de la fonction cosinus, nous donne la formule approchée:

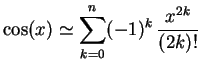
$\bgroup\color{black}$\displaystyle \cos(x) \simeq \sum_{k=0}^{n} (-1)^k \, \frac{x^{2k}}{(2k)!} $\egroup$

I.a)

A l'aide de la formule précédente, écrire un script qui calcule la valeur approchée de cosinus pour une valeur donnée par l'utilisateur.

On sera particulièrement attentif à deux choses :

le factoriel aux dénominateur empèche de prendre des valeurs de trop grandes bien que le terme général de la suite tende vers 0. Il faut équilibrer le calcul de $\frac{x^{2k}}{(2k)!}$ en décomposant celui-ci sous une forme $\frac{x^{2k}}{(2k)!}=\frac{x^2}{1\times 2}\frac{x^2}{3\times 4}...\frac{x^2}{(2k-1)\times 2k}$ .
du fait que le terme générale tende vers 0, on prendra comme critère de choix de le moment où le terme générale ne contribue plus à la somme.

Calculer $\cos(39)$ (réponse : $\cos(39)\simeq 0.26664293235994$ ).

I.b)

Tracer suivant $0 \leq k \leq n$ , le terme $\frac{x^{2k}}{(2k)!}$ pour le calcul de $\cos(39)$ . Expliquer l'erreur constatée.

I.c)

Toujours à l'aide de la série entière, trouver et justifier une méthode pour calculer avec plus de précision (autant que possible) $\cos(39)$ . On comparera le nombre de décimales exactes par rapport à la question a).

Indication: on peut éventuellement utiliser la valeur de $\pi$ (mot clef Scilab : %pi).

Il est possible de construire de nombreux exemples de ce type, avec entre autre, le développement en série entière de $\bgroup\color{black}$ e^{-x}$\egroup$ pour $\bgroup\color{black}$ x>0$\egroup$ . L'astuce pour le calcul et de transformer le calcul de la suite alternée en une suite à termes positifs $\bgroup\color{black}$ e^{-x}=\frac{1}{e^x}$\egroup$

Exercice II :

Soit la famille d'intégrales :

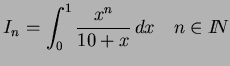
$\bgroup\color{black}$\displaystyle I_n=\int_0^1 \frac{x^n}{10+x} \,dx \quad n \in I\!\!N $\egroup$

II.a)

Montrer que $I_0= \ln \frac{11}{10}$ et que l'on a la récurrence $I_n=\frac{1}{n}-10I_{n-1}$ .

II.b)

Montrer l'approximation:

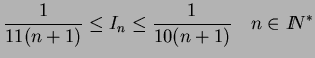
$\displaystyle \frac{1}{11(n+1)} \leq I_n \leq \frac{1}{10(n+1)} \quad n \in I\!\!N^*$

II.c)

Écrire un programme qui calcule, à partir de la relation de récurrence initialisée avec $I_{0}$ : $I_{5}$ , $I_{10}$ et $I_{30}$ . Vérifier les inégalités précédentes et expliquer ce qui ce passe.

II.d)

Même question que c) mais par récursion inverse (décroissante), en partant de l'approximation $I_{n} \simeq \frac{1}{10(n+1)}$ pour n suffisamment grand. Calculer

(

) $I_{5}$ , $I_{10}$ et $I_{30}$ . Analyser et commenter.

Les exemples sont multiples et illimités comme : $\bgroup\color{black}$ J_n=\int_1^e$\egroup$ ln $\bgroup\color{black}$ (x)^n \,dx \quad n \in I\!\!N $\egroup$ ...

suivant: Graphiques monter: intsci précédent: Variables et types de Table des matières

2003-10-15