Les grandeurs physiques de base sont la longueur (L), la masse (M) et le temps (T); les autres grandeurs s'expriment à partir de celles-ci. Une vitesse, par exemple, est une longueur divisée par un temps; on exprime ceci rapidement en disant que la dimension de la vitesse est L/T. Les grandeurs physiques sont exprimées dans le Système International (SI) dont les unités de bases sont le mètre(m), le kilogramme(kg) et la seconde(s). L'unité de vitesse est donc le mètre par seconde m/s.
Isaac Newton, en énonçant ses lois de la mécanique a donné un sens précis à la notions de force. Une force est une action exercée par un objet mécanique sur un autre, susceptible de modifier la position et la vitesse de ce dernier.
Un objet mécanique soumis à aucune force conserve sa quantité de mouvement. S'il est immobile il le reste, s'il a une vitesse il la conserve en direction et en grandeur.
Un objet de masse m soumis à une force F est accéléré. La force, l'accélération a et la masse sont liées par l'égalité:
F = ma soit a = F / m.
Soit deux objets en contact en un point A. Si le premier exerce en ce point une force F sur le second, celui exerce en retour la force -F sur le premier.
En hommage à Newton, l'unité de force du système SI est le newton, N en notation abrégée. C'est la force qui, appliquée à un objet de masse 1kg, lui communique une accélération de 1m/s/s.
Dans l'énoncé de la deuxième loi il est sous-entendu qu'il n'y a pas d'autre force que F appliquée au point considéré. Lorsque'une force F est appliquée à un objet de masse m, on dit parfois, par abus de langage, que cet objet est soumis à l'accélération a = F/m, sans se préoccuper de savoir si F est la seule force appliquée à cet objet. Ce est soumis est une abréviation commode pour serait mis en mouvement avec cette accélération si aucune autre force que F n'intervenait. Debout sur le sol, je dirais par exemple, je suis soumis à l'accélération de la pesanteur. Je suis bien soumis à la force de pesanteur, mais je ne suis pas accéléré. Parce que, outre la force de pesanteur, conformément à la troisième loi de Newton, je suis soumis à la force de réaction du sol qui est exactement l'opposée de mon poids.
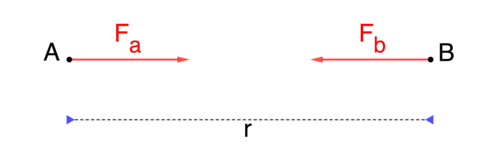
Soit A, B deux points à la distance r l'un del'autre.
La loi de gravitation énoncée par Newton (encore!)
dit que deux objets ponctuels (c'est à dire de dimensions
quasi-nulles) placés en A et B, de masses
respectives ma et mb
sont attirés l'un vers l'autre par deux
forces Fa, Fb
de sens opposés et de même module F = G ma
mb / r2
Le nombre G = 6.6732 10−11 m3 kg-1s-2 est la constante universelle de la gravitation.
La force de gravitation est faible. Faites le calcul dans le cas de deux masses d'une tonne éloignées de deux mètres. Vous devriez trouver F = 0.000017 N.
Et pourtant, sans cette force il n'y aurait ni planètes ni étoiles. C'est elle qui a poussé les particules isolées à se regrouper en amas de plus en plus importants. La force de gravitation est la principale composante de la force de pesanteur qui tend à ramener les objets vers le sol.
Reprenons la formule de la gravitation universelle, en supposant
que l'objet placé en A est fixé, et regardons de plus près
l'attraction exercée sur un objet de masse mb placé en B.
Si B n'est soumis à aucune autre force que
l'attraction Fb de A, son accélération est
Fb / mb.
C'est le vecteur gB
d'origine B, dirigé vers A et de module
F / mb = G ma/r2,
qui ne dépend que de la masse ma de A et de la
distance r séparant B de A. Quelle que que soit la masse
m placée en B, elle est soumise à la même
accélération gB. C'était la
thèse défendue par Galilée, la vitesse de chute libre
est la même pour tous les corps (bien entendu ceci
n'est vrai que pour deux corps tombant dans le vide, car un corps en
chute libre dans l'atmosphère est soumis, outre la force de pesanteur,
à la résistance de l'air).
Par sa seule présenc en A la masse ma modifie l'espace environnant, par l'apparition en chaque point B du vecteur accélération gB qui est l'accélération subie par un objet quelconque placé en B.
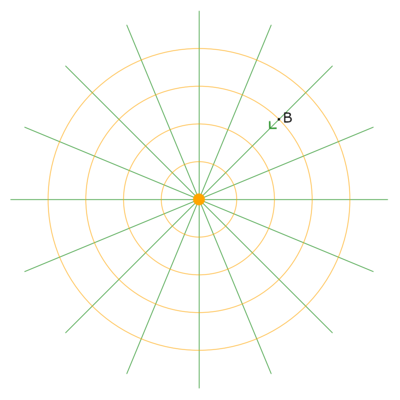
Une fonction associant un vecteur à chaque point de l'espace s'appelle un champ de vecteurs. On ne peut pas représenter un champ de vecteur par une figure, car il faudrait dessiner en chaque point le vecteur correspondant. On le représente en traçant quelques lignes de champ. Une ligne de champ est une courbe qui en chacun de ses points à la même direction que le champ. Les lignes de champ nous renseignent ainsi sur la direction des vecteurs du champ, mais pas sur leurs modules.
Les lignes du champ de gravitation d'un objet ponctuel en A sont particulièrement simples, ce sont les demi-droites aboutissant en A. La figure en montre quelques unes. Sur cette figure sont aussi tracés quelques courbes, les cercles de couleur orange. Chacun d'eux est orthogonal à toutes les lignes de champ.
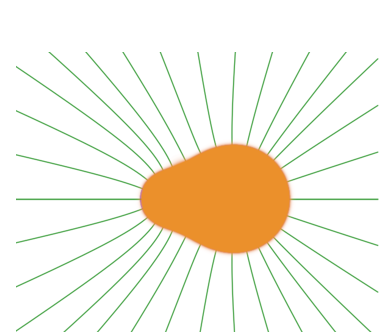
Un objet S non réduit à un point modifie lui aussi l'espace environnant. Le champ gravitationnel de S associe à tout point B l'accélération à laquelle est soumis un objet ponctuel placé en B. Si vous souhaitez plus de détails, voir attraction composées.
La figue ci-contre montre les lignes de champs d'un tel corps. On peut remarquer que ces ne sont pas des droites.
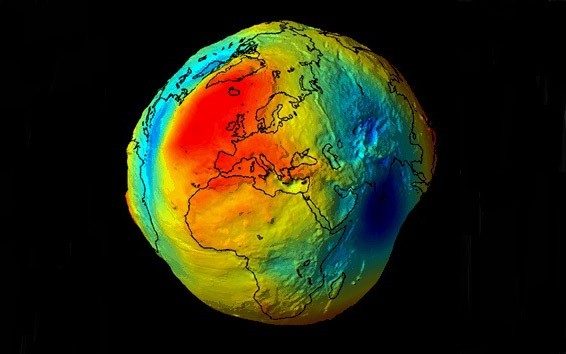
Le calcul effectif du champ gravitationnel d'un solide S suppose connue avec une bonne précision la distribution des masses à l'intérieur de S ce qui est rarement le cas. Avec une connaissance approximative de la distributions des masses on ne peut qu'obtenir une valeur approximative du champ de gravitation. Dans le cas de la Terre en particulier on n'a qu'une connaissance très grossière de cette distribution.
Nous connaissons tous la destination d'un objet livré
à lui même. Ce savoir acquis au bout de quelques mois, est le
fruit des premières expériences de Physique de
bébé qui, sans se lasser, depuis sa chaise haute,
pousse sa cuillère hors de la table et se penche pour
vérifier encore une fois qu'elle n'a pas disparu.
Le poids d'un objet est la force qui tend à le
ramener au sol. Cette force est pour l'essentiel due à
l'attraction gravitationnelle de la Terre. Si la Terre ne
tournait pas sur elle-même le poids serait exactement égal à
cette force d'attraction.
La verticale en A est la direction suivie par la petite cuillère du bébé. Mais on la visualise mieux à l'aide d'un fil à plomb suspendu en A.
La notion d'horizontalité est moins évidente. Le plan horizontal en A est le plan passant par A et perpendiculaire à la verticale de A. On y accède ainsi facilement.
Pour nos ancêtres lointains la terre était évidemment plane. L'oeil humain, même au bord de la mer, est incapable de percevoir la courbure de l'horizon. Les premiers indices pouvant faire douter de la planéité de la terre furent peut-être:
Au VIeme
av. J-C, des philosophes grecs, comme
Anaximandre, affirment que la Terre est une sphère.
Environ 200 ans avant J-C, Eratosthène a donné une
estimation du périmètre de l'équateur assez
proche de 40 000 km.
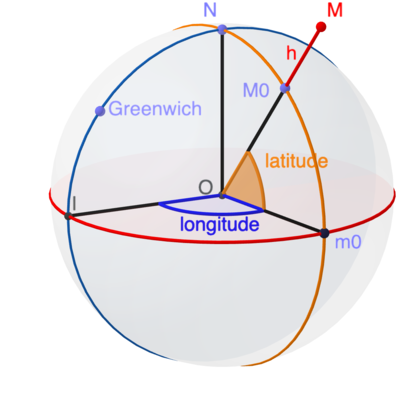
Le plan équatorial est le plan passant par le centre O et perpendiculaire à l'axe polaire ON. L'équateur, tracé en rouge, est l'intersection de ce plan avec la surface de la sphère. Le demi-cercle bleu reliant le pôle Nord au pôle Sud en passant par Greenwich (G sur la figure) est le méridien origine. Il coupe l'équateur en I.
La position d'un point M au sol ou à son voisinage est caractérisée par trois nombres, sa longitude, sa latitude et son altitude. On trace la droite OM qui rencontre la sphère en M0. Le demi cercle orange reliant les pôles en passant par M0 est le méridien de M. Il recoupe l'équateur en un point m0.
En 1671, l'abbé Picard, après avoir grandement contribué à développer les techniques de triangulation suggère que la terre n'est pas parfaitement sphérique, qu'elle semble s'aplatir vers l'équateur. Les mesures s'accumulent peu à peu pour confirmer cette hypothèse. Newton, par un raisonnement purement théorique basé sur la loi de la gravitation qu'il venait d'énoncer, affirme que la forme de la terre est celle d'un ellipsoïde.
Les mesures récentes montrent que rayon de l'équateur est R = 6378 km, tandis que la distance ON du centre au pôle Nord est 6356 km. Le modèle sphérique est resté satisfaisant tant que la technologie ne permettait pas d'évaluer le rayon terrestre avec une précision meilleure qu'une vingtaine de kilomètres.
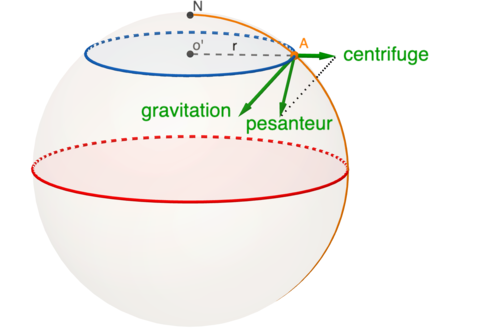
Nous sommes tous montés sur un manège et avons constaté que nous tenons debout sans effort près du centre, mais que, plus on s'en écarte, plus il est difficile de garder l'équilibre. Plus précisémement soit M un objet de masse m, entraîné dans un mouvement circulaire uniforme de centre O', de rayon r et de vitesse angulaire ω. Il est soumis à une force appelée f, la force centrifuge, de direction O'M et d'intensité mω2r. Ainsi, sur la Terre en rotation, chaque objet est soumis à d'une part à la force gravitationnelle Fg, mais aussi à la force centrifuge f. La force de pesanteur, c'est à dire le poids de l'objet est la somme de ces deux forces.
Si l'on préfère parler en terme d'accélération plutôt que de force, la force centrifuge f applique à M une accélération centrifuge d'intensité ω2r. L'accélération de gravitation et l'accélération centrifuge s'ajoutent pour donner l' accélération de la pesanteur.
La figure pourrait faire imaginer que les accélérations gravitationnelle et centrifuge sont de même ordre de grandeur, car on a considérablement agrandi la seconde pour qu'elle soit visible. C'est sur l'équateur que l'accélération centrifuge est la plus forte de valeur ω2 R = 0.034 m/s/s. L'accélération gravitationnelle est partout proche de 9.8 m/s/s donc environ 300 fois plus forte que l'accélération centrifuge.
Bien qu'elle soit assez faible la force centrifuge a aussi une influence sur la forme de la terre elle-même. C'est elle qui est la cause de l'aplatissement du globe terrestre vers l'équateur.
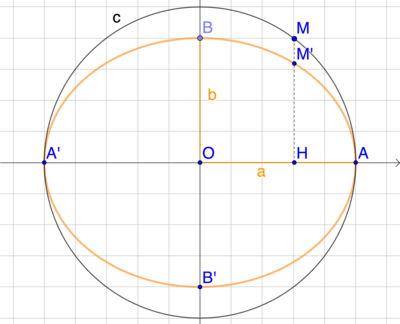
Soit a, b deux nombres positifs a < b. On construit une ellipse grand axs 2a et de demi petit axe 2b obtenue en partant d'un cercle de rayon a et en réduisant d'un facteur b/a les longueurs orthogonales au diamètre A'A.
L'aplatissement de cette ellipse est le nombre (a-b)/a. Si a=b, l'ellipse est un cercle et l'aplatissement est 0.
Sur la figure, en orange, l'ellipse d'axes a = 5, b = 4, d'aplatissement 1/5. On passe, par exemple, du point M sur le cercle, au point M' sur l'ellipse, en multipliant la longueur HM=4 par 4/5 =0,8 pour obtenir HM'= 3,2.
En faisant tourner une ellipse E autour de l'un de ses axes on obtient un ellipsoïde de révolution. Ci-contre l'ellipsoïde obtenu en faisant tourner l'ellipse du paragraphe précédent autour de son petit axe. Les deux extrémités B' et B de l'axe de rotation sont les pôles de l'ellipsoïde.
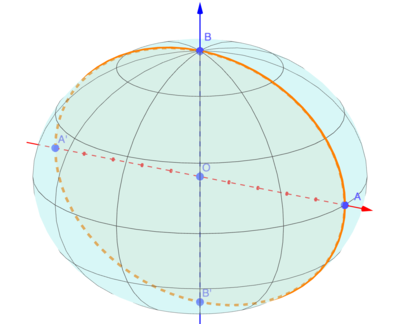
Les plans perpendiculaires à l'axe de la rotation coupent l'ellipsoïde selon des cercles qui sont les parallèles. En coupant l'ellipsoïde par le plan passant par le centre O on obtient l'équateur.
Les plans contenant l'axe de rotation sont appélés les plans méridiens. Ils coupent l'ellipsoïde selon les ellipses déduites de E par rotation. Chacune de ces ellipses est partagée en deux par l'axe. Ces deux moities sont deux méridiens opposeés
Avec l'avènement de la géolocalisation par satellite, un ellipsoïde s'est imposé comme la référence mondiale, l'ellipsoïde GRS80 de l'IAG (Association Internationale de Géodésie), appelé aussi WGS 84. Il est l'unique référence légale en France depuis le 5 mars 2019, (RGF93). Son axe de révolution est l'axe SN reliant le pôle sud S au pôle nord N. Le demi grand axe a est le rayon de l'équateur a = 6 378 137, 000 m et le demi petit axe est b = ON = b = 6 356 752, 314 m.
Comme dans le cas du mdèle sphérique chaque point de l'espace peut être caractérisé par 3 coordonnées, une longitude, une latitude et une hauteur.
Le plan méridien d'un point M est le plan contenant l'axe
polaire et le point M. L'intersection
de ce plan avec l'ellipsoïde est l'ellipse orange ci-contre. Elle
coupe l'équateur en un point m0.
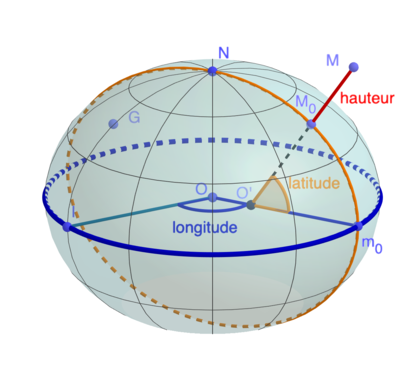Le point M0 est la projection orthogonale de M sur
l'ellipsoïde, et le point O' est l'intersection de
M0M, la verticale en M0, avec le plan de l'équateur.
Le méridien origine des longitudes est celui qui passe par l'observatoire de Greenwich; il coupe l'équateur en I.
Dans le cas de la sphère la latitude était l'angle (Om0, OM0). Cet angle appellé la latitude géocentrique de M ne présente pas d'intérêt physique ni géographique. La droite qui a une signification physique c'est la droite M0M, la verticale en M0. Le point O' est toujours entre O et m0. Autrement dit la latitude géocentrique est toujours inférieure à la latitude géographique. Par exemple, la latitude géocentrique du parallèle de latitude 45° est de 44°48'.
Quand on s'intéresse à la forme de la terre, on s'intéresse à un objet imaginaire, la terre à l'altitude 0 obtenue en rasant tous les reliefs au niveau des mers. Mais qu'est ce que le niveau de la mer à l'intérieur des terres?
On peut donner un sens à cette expression en utilisant la notion de surface horizontale. Une surface horizontale est une surface qui, en chacun de ses points, est perpendiculaire à la verticale. Cette définition a un sens même sous la surface de la Terre, car la verticale, la direction du champ de pesanteur est partout définie.
La surface d'un lac, la surface des oceans par temps calme sont des surfaces horizontales, car si le niveau de l'eau reste constant c'est précisément parce que la force de pesanteur est perpendiculaire à la surface de l'eau.
Une surface de niveau est une surface horizontale qui recouvre tout le globe terrestre. Les surfaces de niveau sont emboitées les unes dans les autres comme des poupées russes. Le Géoïde est alors défini naturellement commme la surface horizontale qui, en dehors des terres, coïncide avec le niveau moyen des mers.
A l'aide des équations de Newton, Mac-Laurin a démontré rigoureusemt en 1741 que si la terre n'était composée que d'une matière fluide homogène de densité constante, comme de l'eau, par exemple, le géoïde serait un ellipsoïde de révolution. Mais la terre n'est pas un fluide homogène, et la surface des océans ne coïncide pas avec une forme géométrique simple. Les mesures récentes effectuées par des satellites montrent que le niveau des mers s'écarte légèrement de l'ellipsoïde WGS84, parfois au dessus, parfois au dessous, mais jamais de plus de 80 m.
Puisque le Geoïde ne coïncide pas avec l'ellipsoïde, la hauteur ellipsoïdale du point du géoïde de longitude et latitude φ, λ est non nulle. On l'appelle l'ondulation du géoïde ou encore l'anomalie du géoïde en ce point.
La carte ci-dessous donne les valeurs, en mètres, de l'anomalie du géoide sur la France continentale. Elles oscillent entre 43 m et 53 m.
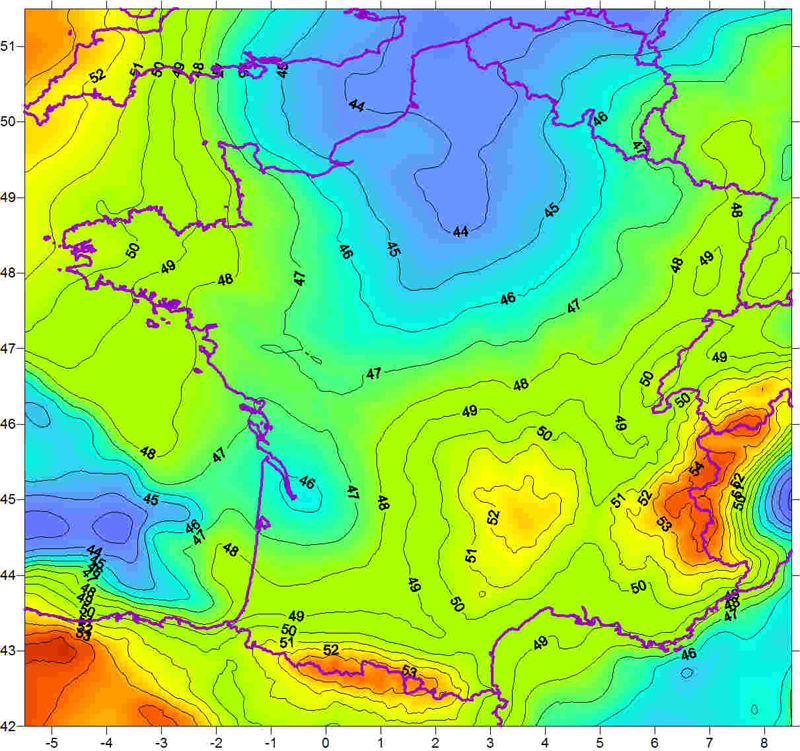
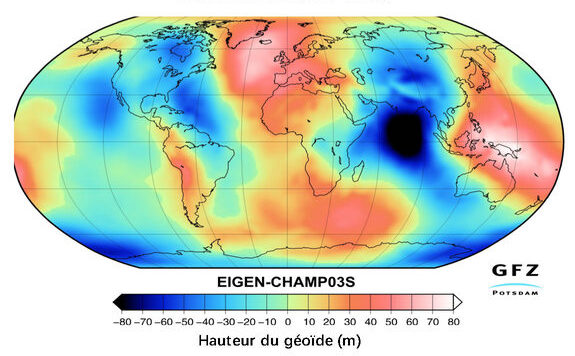
L'ellipsoïde GRS80 ne privilégie aucune région. La carte
suivante montre que partout sur Terre, l'anomalie du
géoïde est comprise entre -80 m et +80 m.
Le Système de Positionnement par Satellite mis en place par le gouvernement américain est opérationnel depuis 1995. Il repose sur 24 satellites répartis sur 6 orbites à 20200 km d'altitude de sorte que, de tout point de la Terre, 4 satellites au moins soient visibles. Chaque satellite envoie régulièrement un message composé de sa position spatiale et de la date d'expédition du message. Un récepteur GPS, mon téléphone par exemple, après quelques tatonnemments, parvient à synchroniser son horloge avec le temps GPS, le temps partagé par les satellites, puis, en comparant, pour chacun des messages, sa date de réception et sa date d'expédition il calcule sa distance à la position du satellite émetteur au moment de l'émission. Il connait alors sa distance à au moins quatre points dont il a les coordonnées. Un dernier calcul lui donne ses propres coordonnées, qu'il convertit en coordonnées ellipsoïdales, longitude, latitude, hauteur au dessus de l'ellipsoïde.
La vitesse de la lumière dans le vide est c = 299 792 458 m/s, valeur exacte, parce que c'est la définition du mètre. La distance d d'un satellite est obtenue en comparant la dates d'émission de son message avec la dates de réception. Si dt est l'écart séparant ces deux dates, d est le chemin parcouru par la lumière pendant l'intervalle de temps dt, c'est à dire d = c dt. Une erreur de 1μs sur la valeur de dt se traduira par une erreur de 300m sur la valeur de d. Pour espérer une erreur inférieure au mètre sur l'évaluation des distances il faut mesurer les dates avec une précision de l'ordre du millardième de seconde, c'est à dire la nano-seconde. C'est pourquoi il est indispensable de synchroniser l'heure du téléphone avec l'heure des satellites du système GPS, que nous appellerons l'heure GPS.
Si cette synchronisation est indispensable ce n'est pas dû à un manque de précision de l'horloge du téléphone qu'il faudrait remettre à l'heure, mais à une raison plus profonde, l'heure terrestre, n'est pas la même que l'heure GPS. A cause de leur mouvement autour de la terre, conformément aux lois de la Relativité d'Einstein, le temps des horloges GPS s'écoule un peu plus vite que celui des horloges terrestres. Chaque jour il prend une avance de 38µs de plus sur l'heure terrestre.
Ce problème de synchronisation étant résolu, il reste des sources d'erreur, dont la principale est que, au voisinage de la Terre, la vitesse c de la lumière n'est pas exactement la même que dans le vide absolu. Si l'on ne tient pas compte de ce phénomène la précision obtenue est de l'ordre de quelques mètres. En utilisant des récepteurs gps plus sophistiqués qu'un téléphone mobile, tous les satellites disponibles ainsi que des informations très précises sur leurs trajectoires fournies par des serveurs GNSS, les usagers professionnels peuvent calculer les coordonnées ellipsoïdales d'un point dans le repère GRS80 avec une précision de l'ordre du centimètre.
Ainsi, il est relativement simple aujourd'hui de situer la position d'un point quelconque dans l'espace avec une précision de l'ordre du cm à l'aide de ses trois coordonnées ellipsoïdales, sa longitude, sa latitude et sa hauteur ellipsoïdales. Mais qu'en est-il de son altitude ? L'altitude d'un point est sa hauteur au dessus du géoïde. Pour calculer l'altitude d'un point au cm près il ne suffit pas de disposer de sa position spatiale au cm près. Il faut déterminer avec la même précision la position du géoïde au voisinage de ce point.
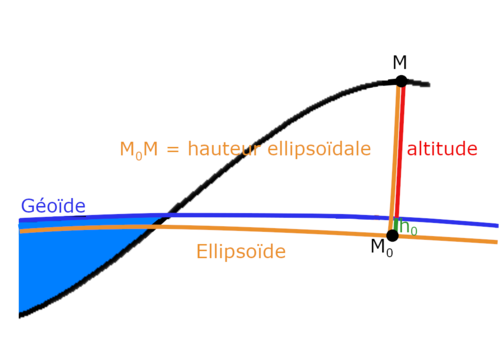La figure ci-contre représente un paysage avec l'océan à gauche, dont la
surface coïncide avec le Géoïde, tracé en bleu. La
surface tracée en orange est l'ellipsoïde. M est le sommet
d'une colline dominant la plage. M0 est la projection
de M sur l'ellipsoïde. Le segment M0M, tracé en
orange donne la hauteur ellipsoïdale h de M. Le petit
segment h0 tracé en vert
donne la valeur de l'anomalie du géoïde en M0.
L'altitude a du point M, est, par définition, sa hauteur au dessus du Géoïde. Elle est donc donnée par la formule a = h - h0. L'altitude ainsi définie s'appelle l'altitude orthométrique.
On ne sait malheureusement pas calculer avec une précision centimétrique l'anomalie h0 du géoïde au voisinage de M.
Bien sûr, en tout point d'un océan, grâce aux observations satellitaires, on a immédiatement accès à la position du géoïde puisque celui-ci coïncide avec la surface de l'eau. Les projet GRACE (Gravity Recovery And Climate Experiment) et GOCE (Gravity field and steady-state Ocean Circulation Explorer) ont permis de calculer l'anomalie du géoïde en les points des océans avec une précision de l'ordre du mm.
Mais, au dessous des terre la position du géoïde n'est connue qu'avec une précision décimètrique.
Depuis 2019 la France utilise une autre définition de l'altitude, l'altitude normale qu'il est plus simple de calculer. Les différences entre altitude normale et altitude orthométrique sont faibles près des côtes, mais de 70 cm au sommet du Mont-Blanc. L'IGN a réalisé des tables appellées grilles de conversion altimétriques. Ces tables donnent la valeur de l'anomalie h0 en tous les points d'un réseau couvrant tout le territoire. Les points de ce réseau sont espacés d'environ 2.5km.
