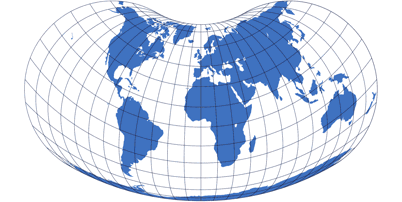
Groups of map projections
Since you can filter by projection type (in the selection by thumbnail), I’d like to offer a brief introduction to the different types available.
I will confine myself mostly to optical differences, I am not going to explain how they are constructed mathematically or why they are called «cylindric» etc.
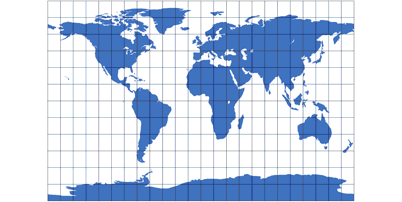
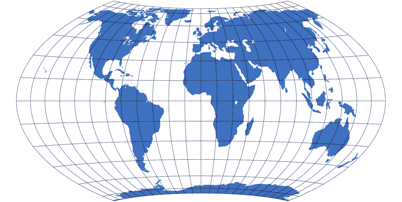
Cylindric Projections
Example: Equirectangular Map
Cylindric projections are rectangular,
meridians and parallels (the circles of latitude) are straight lines at
right angles.
At least as long as you’re viewing the common equatorial aspect – that’s when the equator is at the vertical center and
runs from left to right in a straight line. In other aspects the lines of graticule are curved, as for example
can be seen in the
Cassini projection.
Are all rectangular world maps cylindric projections?
No, although for quite some time, I said something different here.
You should not believe everything I say. ;-)
For example,
Adams World in a Square I
is rectangular but no cylindric projection.
And keep in mind that unless the whole earth is shown the mapmaker always might only present
a rectangular section of a projection that is nowhere near rectangular.
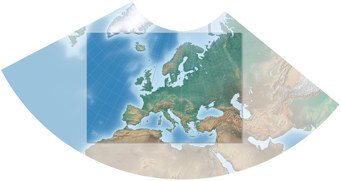
Cutting a rectangular section from Lambert’s conformal conic projection.
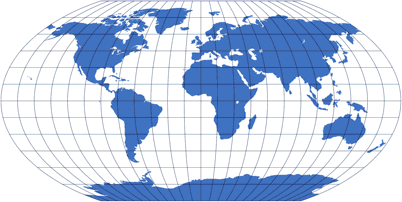
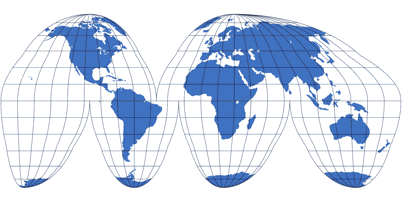
Pseudocylindric Projections
Example: Wagner VI
Pseudocylindric show straight parallels and a straight center meridian, all other meridians are curved – or, in a few cases (e.g. Eckert II), broken.
Pseudocylindric often show a pole line (see schematic of Wagner VI); but also there are pointed poles (e.g. Sinusoidal), sometimes being the apex of an ellipse (e.g. Mollweide)
Meridians are equally spaced along every parallel. That’s why some projections which look like pseudocylindrics at first glance are listed among the Miscellaneous Projections – they lack this property.
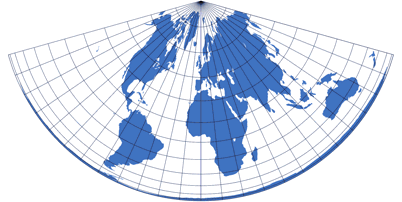
Conic Projections
Example: Lambert Equal-Area Conic
Conic Projections look like cones… or rather, like cones that have been rolled out.
Usually they are not used for world maps but rather for showing a smaller part, i.e. a single continent
or country – except for e.g. the Schjerning I projection,
which was designed for the whole world.
Moreover, you can configure various conic projections to get a halfway decent depiction of the Earth’s surface –
but in the very most cases, you’d be better off with a projection from a different group.
I’ve included a few conic projections, but mostly for the sake of completeness and because I feel they look
interesting, although I do think that it’s not very useful to compare them to other projections.
Lenticular Projections
Example: Wagner VII
Lenticular projections are similar to the pseudocylindric ones. But while those show straight parallels, in lenticular projections the parallels curve toward the poles.
The term lenticular was proposed by Daniel «daan» Strebe in the article
Map Projection Essentials (a highly recommendable article, by the way)
– but as far as I know, the term hasn’t become widely accepted yet.
So why did I adopt it anyway?
The reason is, there is no generally
accepted general term for that kind of projections that are called
lenticular here (and by Strebe).
Some authors divide them into groups named after their mathematical lineage, calling those groups
pseudoazimuthal, modified azimutal, polyconic etc.
Others put them into one group (just like me) but call all of them «polyconic», which is a bit
of a problem since that group includes projections that are genuine polyconics, i.e. derived from
the conics mentioned above – like the
American Polyconic
– as well as projections that definitely aren’t.
And still others stuff them all into the Miscellaneous class, which then contains a large number of projections. That’s quite
inconvenient in my opinion: Miscellaneous should always be a term that refers to a relatively small group which really can’t be identified
otherwise.
Moreover, I really like the term lenticular.
It is also used for galaxies that have a certain shape –
and what is good for galaxies can't be bad for map projections. ;-)
So thank you, daan!
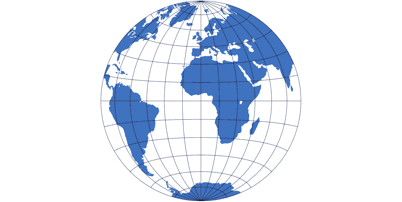
Azimuthal Projections
Example: Lambert Azimuthal
Azimuthal projections are circular.
You can imagine a light source shining through the
spheric Earth, projecting an image onto a screen. Since a sphere will
always cast a circular image, azimuthal projecting are circular, too.
Okay, that’s a somewhat awkward explanation, but basically it’s right.
It also explains the fact that azimuthal projections can
only show a hemisphere of the Earth – or, when extended to display
the full entire planet, have severe distortions towards
the edge of the image.
A few decades ago it was quite common to use azimuthal world maps in atlases, showing the eastern and western hemispheres side-by-side (example: Azimuthal Equal-Area projection). Nowadays they are, like the conic projections, mostly used as an excerpt from the full projection to show smaller parts.
Moreover, I’d like to point out that not all circular projections are azimuthal – some, like Van der Grinten I, belong to the Miscellaneous group.
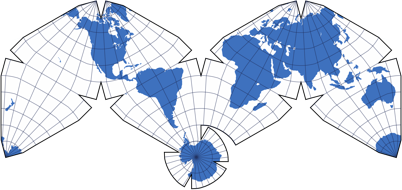
Polyhedral Projections
Example: Cahill-Keyes Projection
The group of polyhedral projections was added to my website not until the beginning of 2019. Mainly because before that, I could generate only very few images of that type. On this type, earth’s surface gets projected to… well, to a polygon (that includes a triangle), which leads to a distinctive shape of the map.
Sometimes you can cut a map of this type into pieces and put them back together differently, resulting in a rectangular shape, like on Kunimune’s IMAGO. Nonetheless, those maps of course still belong to the type of polyhedral projections.
Using a polyhedral projection can lead to comparatively low distortions of shapes and areas, or at least a low range of distortion values.
And what about the interrupted projections?
Example: Goode Homolosine
Actually, there is no group of interrupted projections! They belong to one of the other groups (pseudocylindrics, mostly).
But in terms of comparison – and after all,
comparing projection is what this website is all about –
I thought for quite some times that it’s good idea to
group the interrupted projection separately, so you can set a filter
in the selection by thumbnail.
Meanwhile however I think it’s more appropriate to file them under their genuine type.
After that has been clarified, I’d still
like to mention what’s the benefit in interrupting a projection:
If you remember that it’s impossible to project Earth’s
surface to a flat map without having distortions of some kind,
it’s easy to understand that you can minimize
distortions by interrupting the projection.
After all, an orange’s peel can’t be flattened without being torn apart (to quote a popular example). So you could say that interrupting a projection is inspired by everyday knowledge…
Miscellaneous
Example: Hill Eucyclic
And finally, there’s the Miscellaneous group which covers all projections that don’t fit into the others – not even into the lenticular class, which already is kind of a melting pot.