Equal Area Projections

Examples of Equal Area Projection Maps

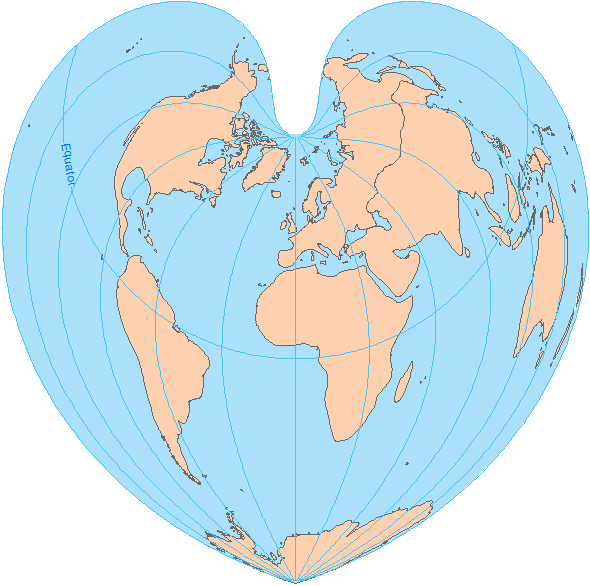
As shown in the examples below, equal-area projection maps preserve the size of features true to their real area.
For example, keep an eye on how Greenland retains its true size of the area throughout each map.

1. Behrmann

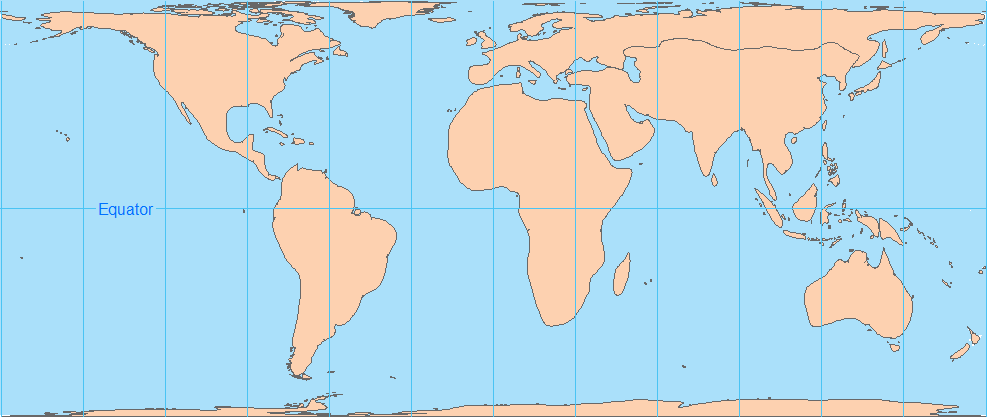
2. Sinusoidal

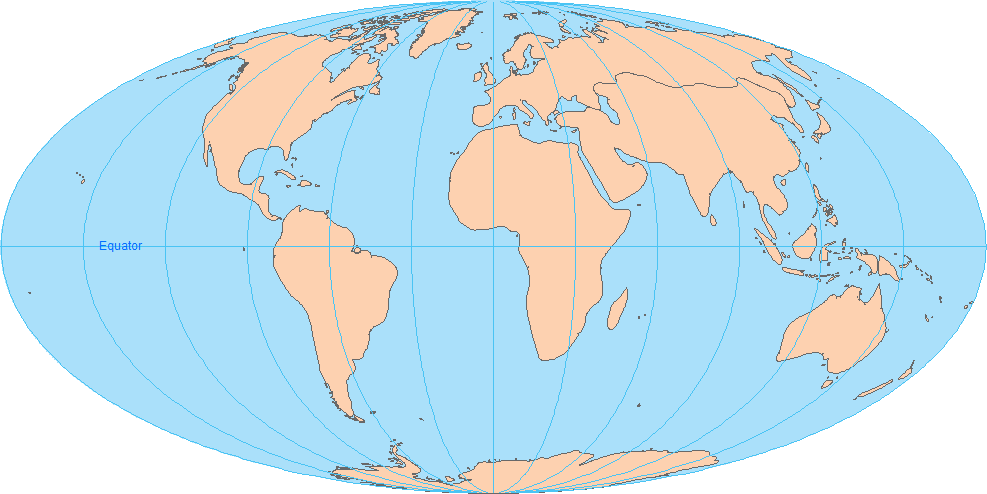
3. Mollweide

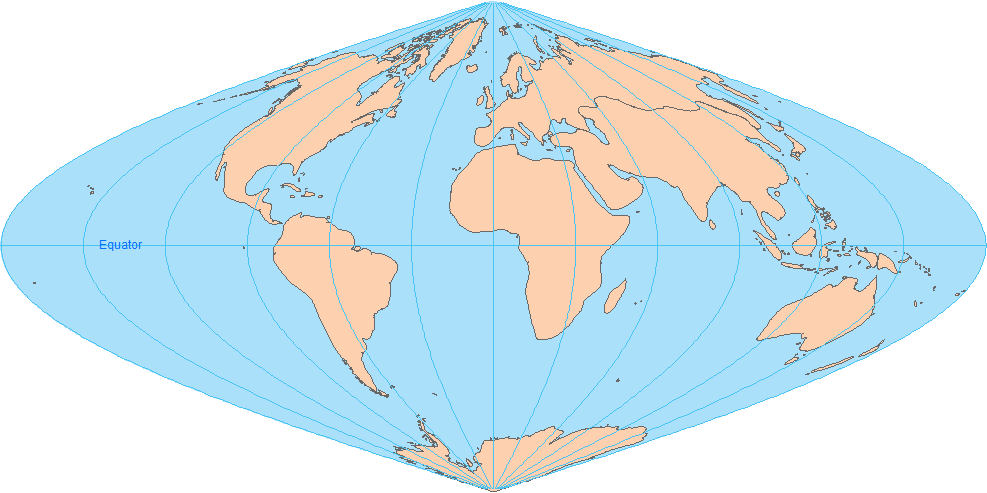
4. Hammer Aitoff

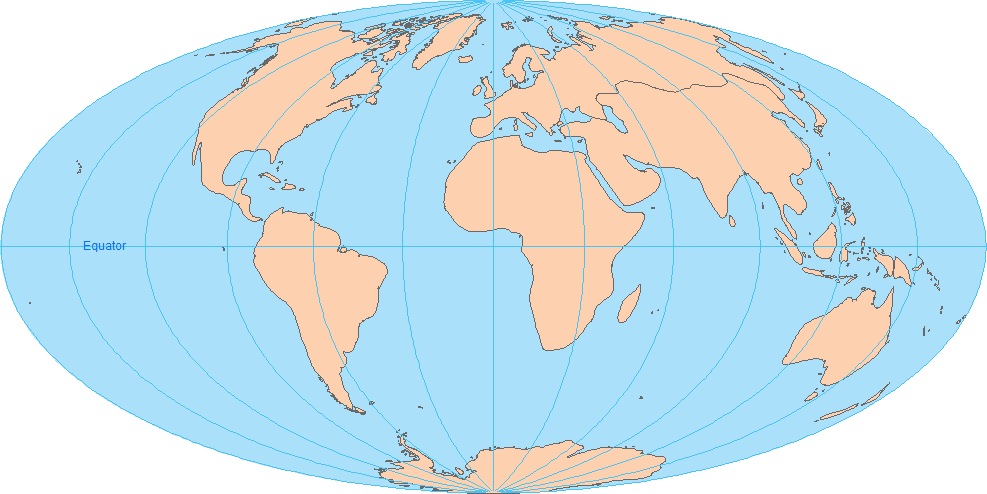
5. Bonne

But if you look at a Mercator projection map below, Greenland becomes abnormally large due to its distortion in the area at the poles.
And Antarctica looks like it’s bigger than all the other continents.

USGS Uses the Albers Equal Area Conic Projection

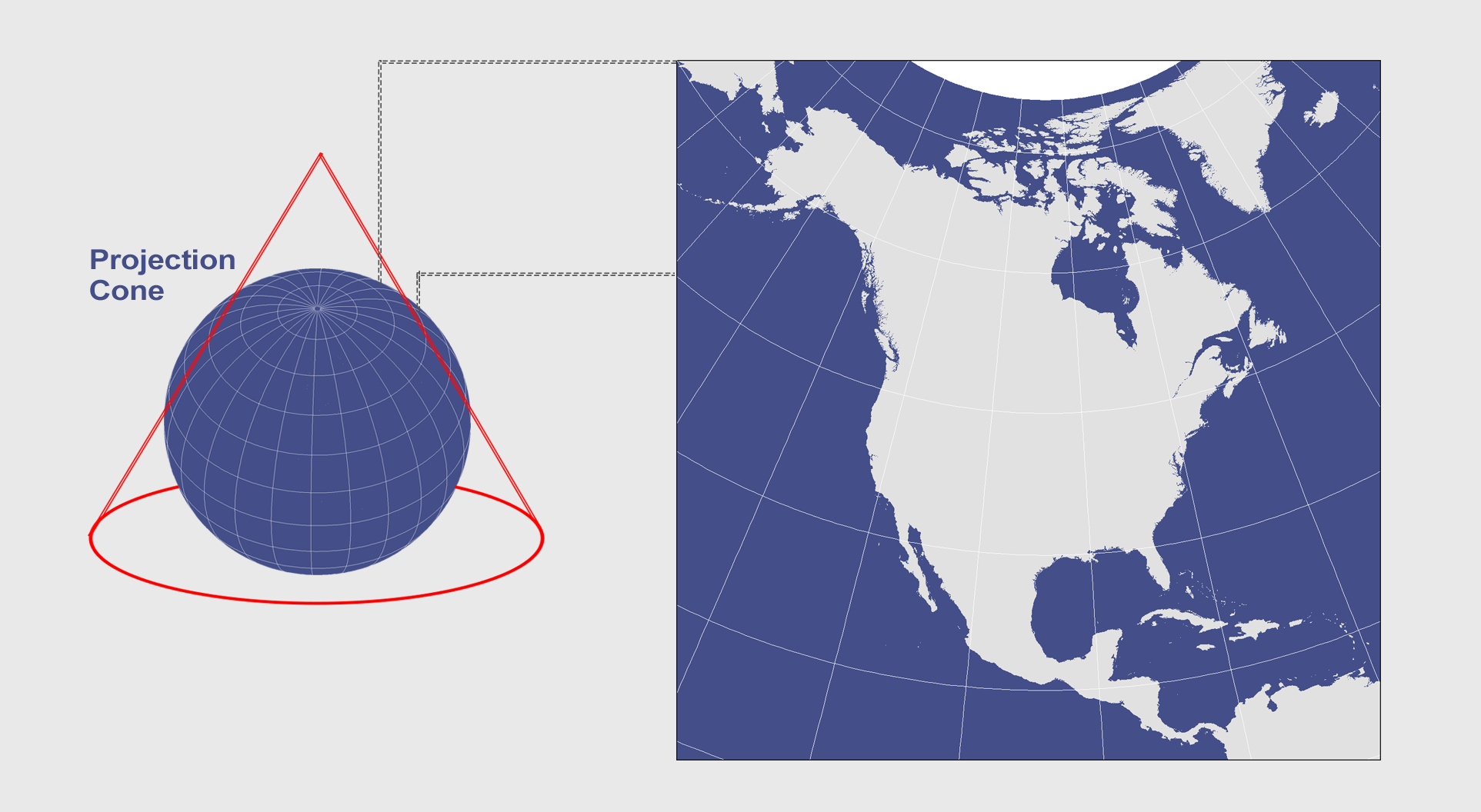
The USGS commonly uses the Albers Equal Area Conic projection because of how it proportionally represents areas for the conterminous United States.
H. C. Albers first introduced this map projection in 1805 with two standard parallels (secant). Since then, cartographers have used it for displaying large countries that require equal-area representation
Like all map projections, the Albers Equal Area Conic Projection distorts other properties in a map. For example, distances and scale are true only on both standard parallels.
Although the direction is reasonably accurate, it’s not conformal, perspective, or equidistant.

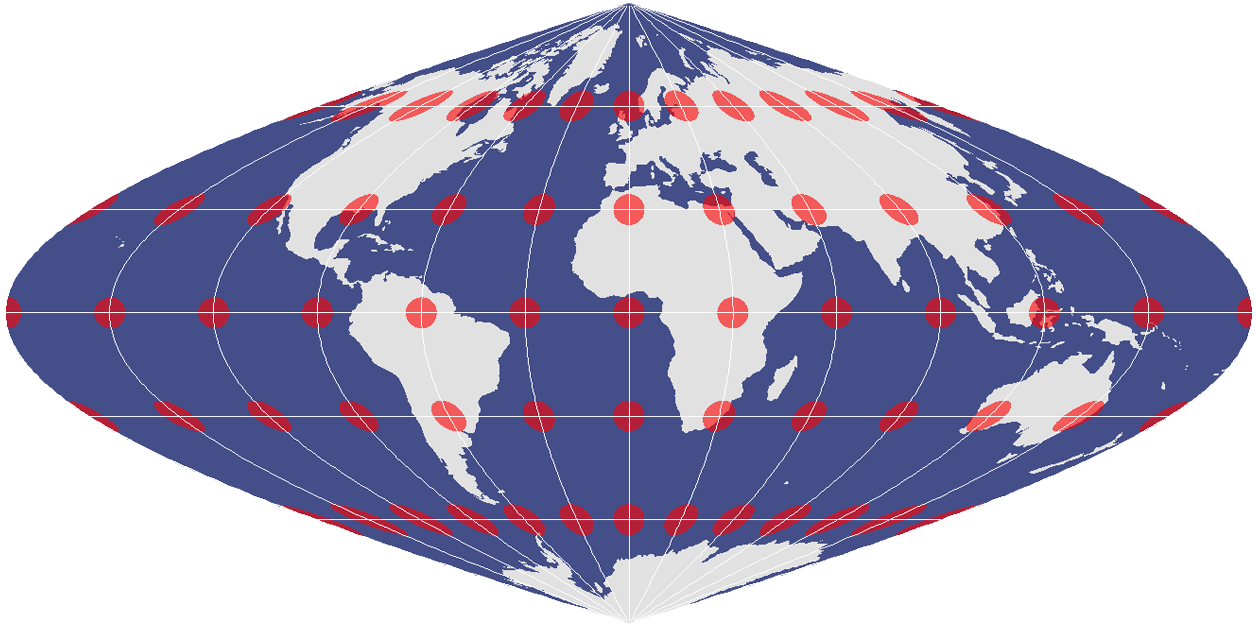
Tissot Circles and Distortion

In an equal area projection, Tissot circles are all the same relative size across the map.
Despite how the Tissot indicatrix changes from a circle to an ellipse, this projection retains relative size.
So now you have an idea of how equal area projections work, we have a section entirely dedicated to the types of distortions found in maps.
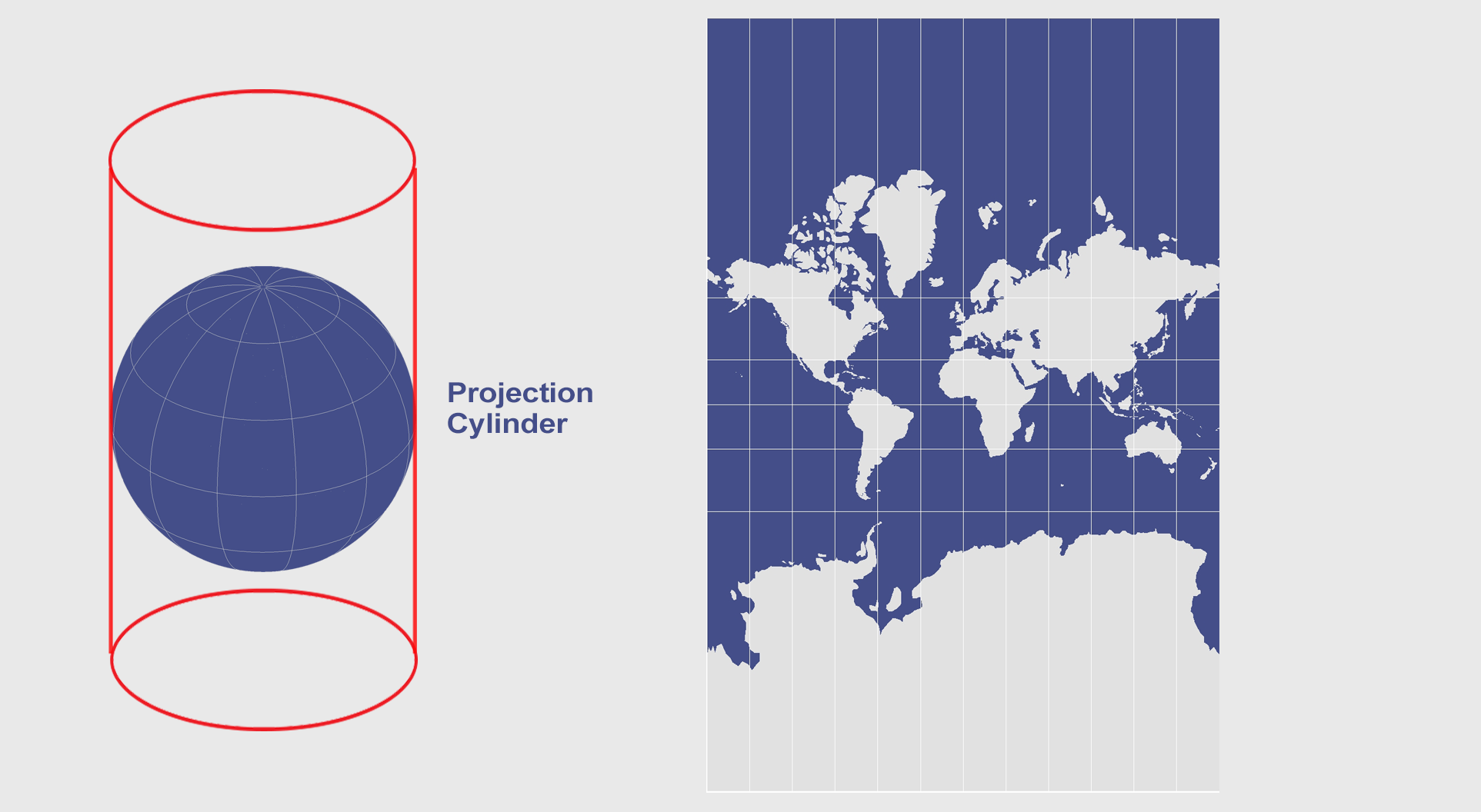
Also, we’ve explained developable surfaces like cones, cylinders, and planes and how they flatten a 3D globe into a two-dimensional map.

	Equal Area Projection Maps
	By: GISGeography Last Updated: November 4, 2023