Map Distortion with Tissot's Indicatrix

Tissot's Indicatrix and Map Distortion

There really is no one best map projection. Each map projection distorts shape, distance, direction, scale, or area and cannot preserve all map properties at the same time.
Map distortion is best understood by looking at Tissot's indicatrix. A Tissot indicatrix contains circles at grid intersections and shows how they vary due to distortion from a map projection
If you really want to know if a map has a conformal, equidistant, or equal-area projection, Tissot's indicatrix can help by showing the magnitude of angular, linear, and area distortion.
Let's examine map distortion using Tissot's indicatrix.

1. The Globe Is the One True King

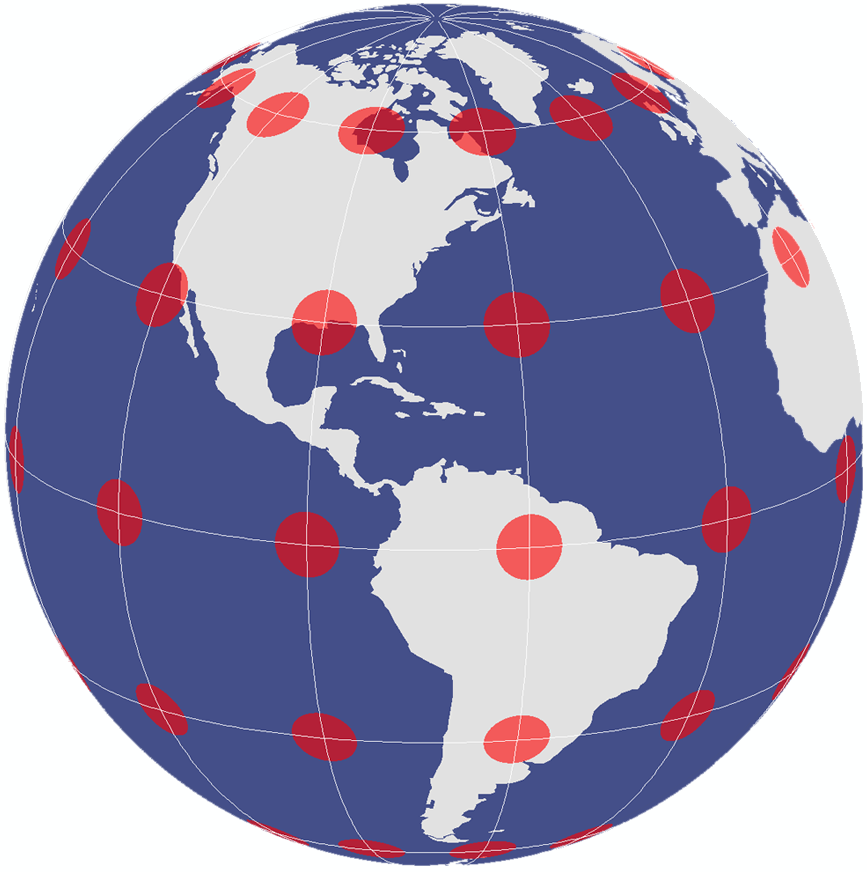
Globe – Conformal, equidistant and equal area

The one true king of representing our Earth is a three-dimensional globe. This is because our globe is the only true surface where directions, distances, shapes, and areas are true.
On a reference globe, the Tissot indicatrices are conformal, equidistant and equal area.
While conformal and equal-area map projections are ‘major properties', equidistant and azimuthal map projections are ‘minor properties'. Minor properties are local in specific regions and may be true for only selected lines.

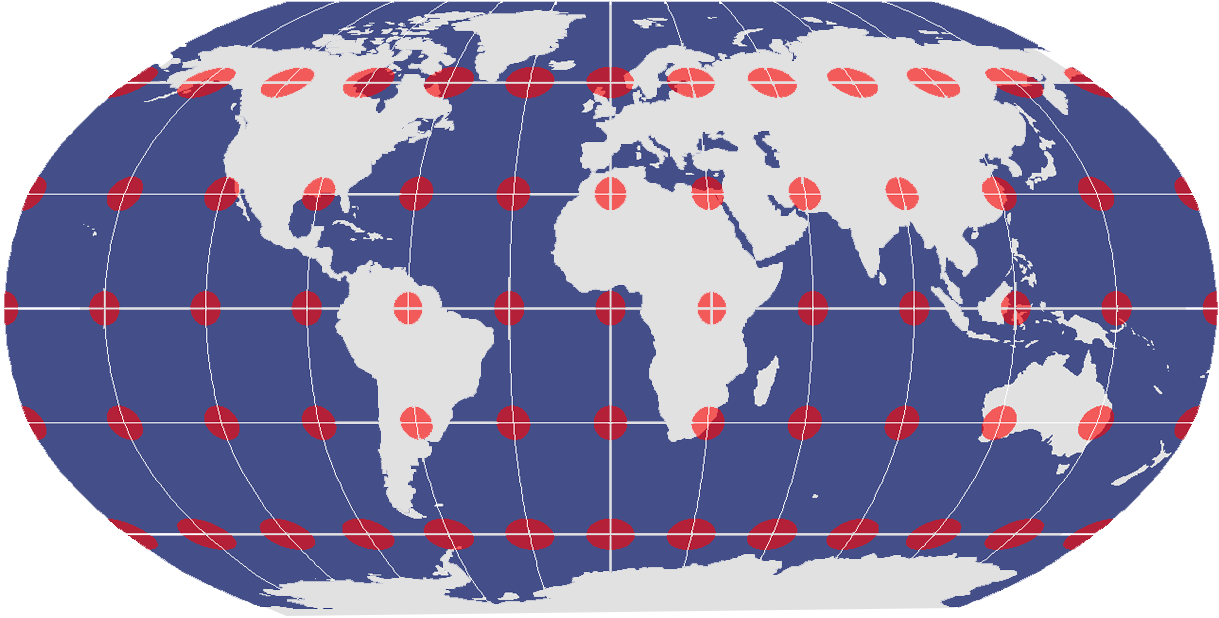
2. The Conformal Projection

North American Lambert Conformal Conic Projection – Conformal

Conformal map projections preserve local angles and shapes. Often, meridians and parallels intersect at right angles. A map projection cannot preserve angles and shapes at the same time.
When a map projection preserves angles such as the Web Mercator projection, the Tissot indicatrix is all circles but different sizes.
For example, the Lambert Conformal Conic projection maintains local angular and shape relationships throughout the map. But conic projections aren't well-suited for mapping extremely large areas.
However, the size of circles varies throughout the map projection, meaning it's not equal area and relative size is not preserved.

3. The Equal Area Projection

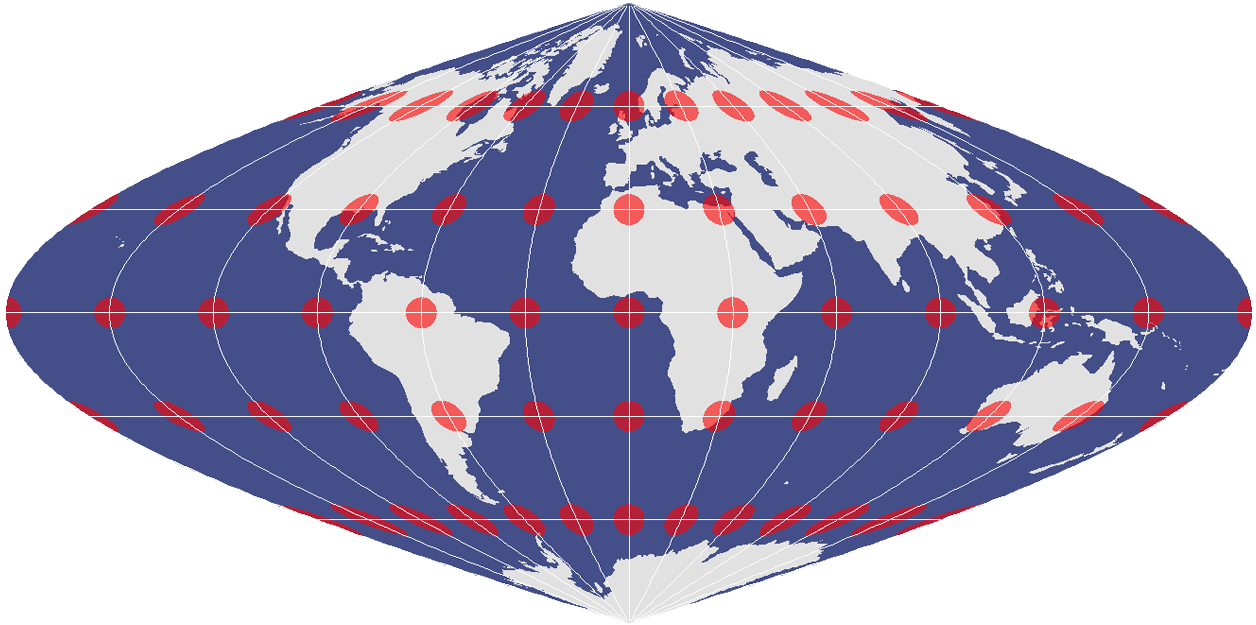
At two given areas in a map, an equal-area projection retains the relative size of areas.
In an equal area projection, Tissot circles are all the same relative size across the map. Despite how the Tissot indicatrix changes from a circle to an ellipse, an equal-area projection retains relative size.
An equal-area projection cannot also be conformal, as their shapes change as shown in the sinusoidal projection. In other words, if the projection preserves area, then it distorts shape (and vice versa).

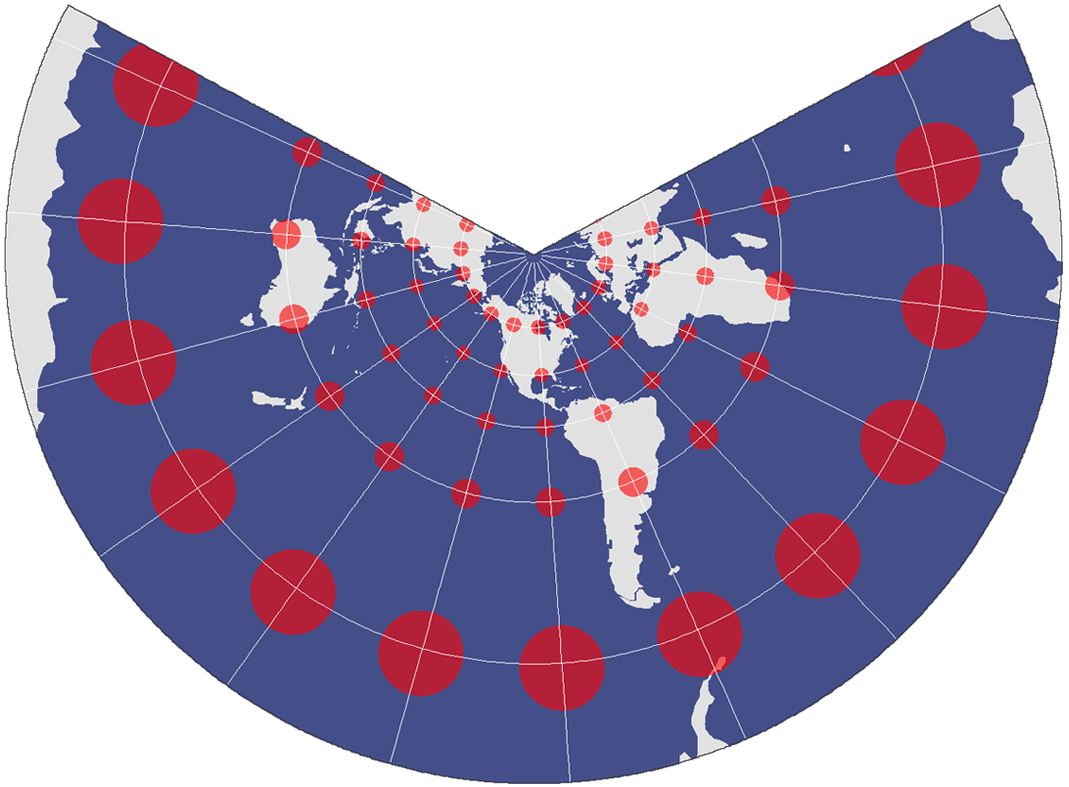
4. The Equidistant Projection

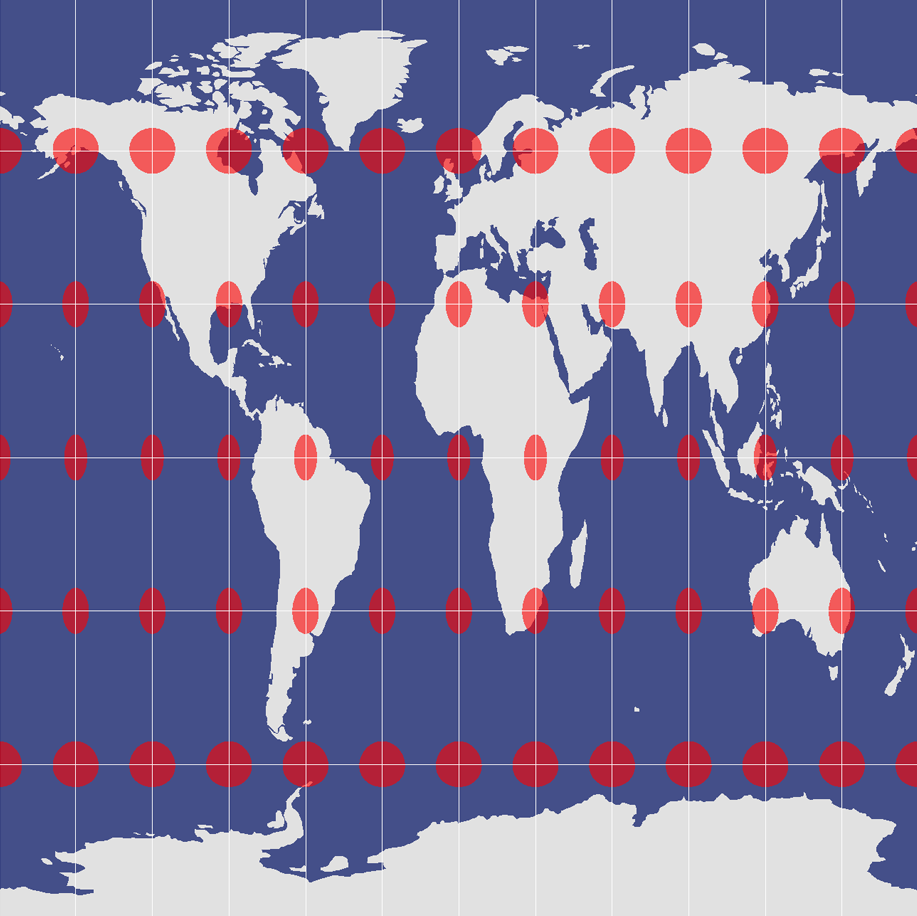
Equidistant Cylindrical Projection – Equidistant

The equidistant projection (or Plate Carrée if the standard parallel is the equator) has a minor map property that maintains distance (or scale) along a set of lines in the map projection. Simply, it produces grids of equal rectangles.
In the case of the equidistant cylindrical projection, distances along the equator and meridians are true distances and only along these sets of lines.
Scale and distance have the same proportional length as that of a globe along specific lines with the equidistant property. However, a line that follows a parallel in the polar region is not the same distance as the equator.

5. The Compromise Projection

A compromise projection minimizes distortion in shape, area, and orientation. However, a compromise projection is neither a conformal projection nor an equal-area projection.
For example, the Robinson projection uses a pseudocylinder to flatten a three-dimensional globe. Even though shape and area distortions are low, its map properties remain distorted.

6. Map Distortions Are Everywhere

No matter how hard you try, every single map projection distorts reality.
Every one.
Whichever map property you want to preserve, you can apply conformal, equidistant, or equal-area projections.
Alternatively, if you want the best of all worlds (with still a bit of distortion), use a compromise projection.

	Map Distortion with Tissot's Indicatrix
	By: GISGeography Last Updated: January 6, 2024