Ivan Gentil                                                    

Avant un peu de maths, quelques informations.

Deux petits graphiques informatifs !  Le premier montre qu'li n'y a pas de révolution mais un  l'empilement de la production d'énergie. Le second illustre où se place notre ère géologique. On a quitté sans plaisir l'holocène en 1950 et nous sommes dans l'anthropocène. La suite est à écrire.









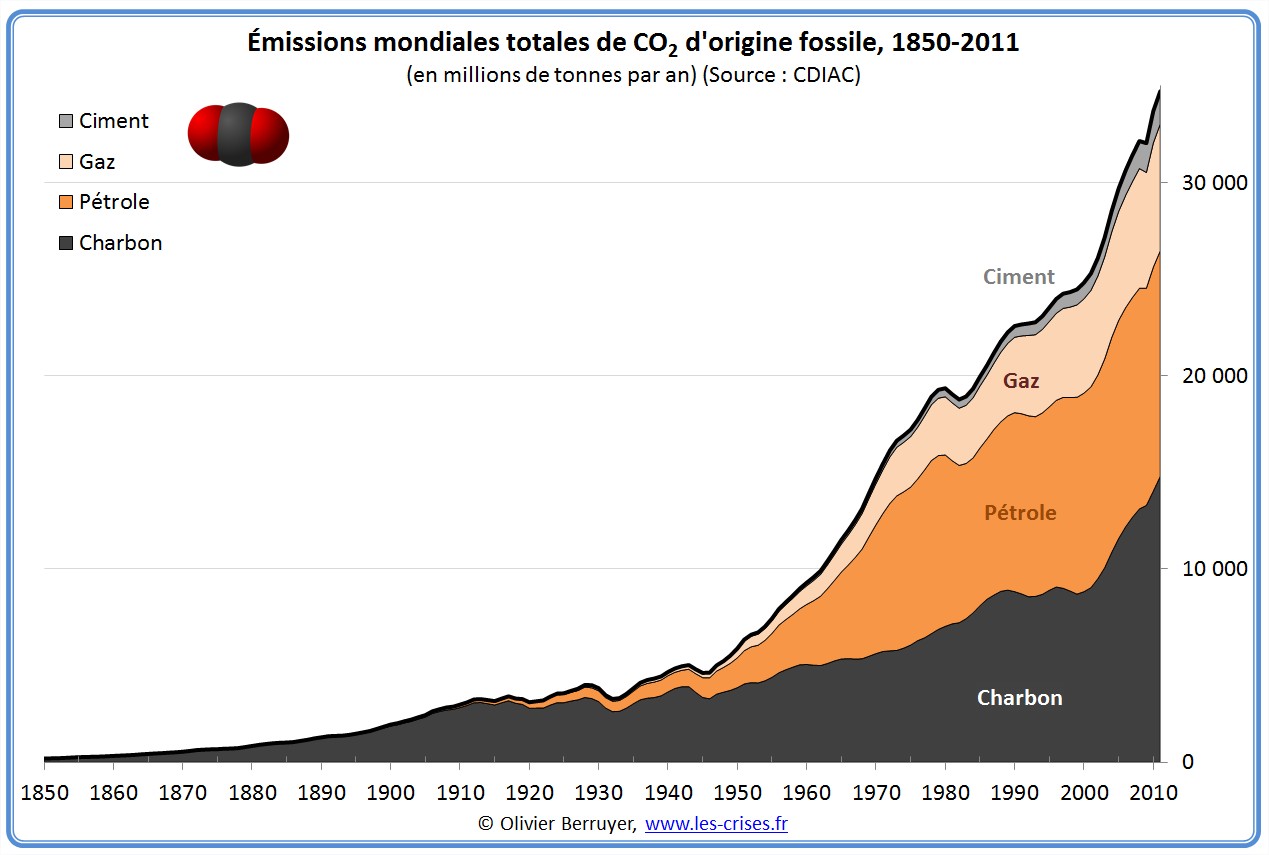
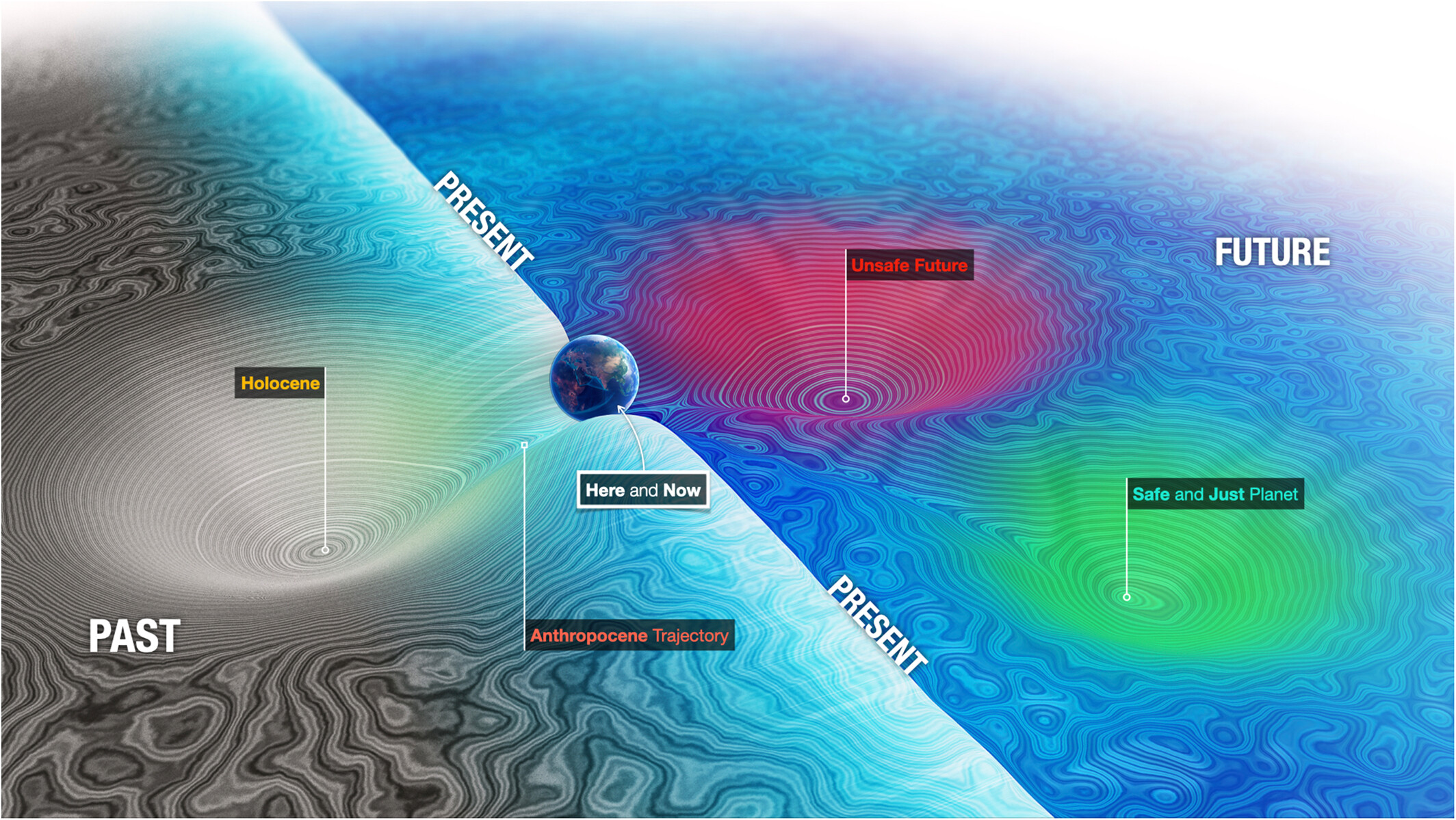
Dans cette vidéo incroyable de 2 minutes, l'évolution du CO2 depuis 800 k années, ou bien le rechauffemnt pas une vidéo inscructive !

Une BD bien écrite sur le sujet, avec même un peu d'humour, de Etienne Lécroart et Ivar Ekeland, tout est dans le titre et dans ce descriptif.

Courriel:   gentil  <~<at>~>  math.univ-lyon1.fr
Bureau : 101B

Téléphone : +33 4 72 44 85 78

Adresse postale :

1. Centre d'intérêts
2. Prépublications
3. Publications
4. Diffusion de la recherche
   
5. Livres de recherche
   
6. Livre d'enseignement
   
7. Proceedings
8. Note
9. Enseignements
10. Thèse et habilitation
11.  Etudiants et jurys de thèses
    
12. Workshops
13. Administration, responsabilités et projets de recherche
    
14. Liens sur des revues friendly
    
15. Séminaires et rencontres mathématiques

Situation: Enseignant-chercheur, Institut Camille Jordan. Luniversité Claude Bernard Lyon 1 est membre de l'UDL. 

Centres d'intérêts :

• Analysis, probabilities and geometry.
• Asymptotic behaviour of diffusion.  
  
• Logarithmic Sobolev, Sobolev and Poincaré inequalities.
• Transportation inequalities.
• Hamilton Jacobi equations.

• A.-L. Fougères, I. Gentil :  Entretien avec Ivar Ekeland réalisé à Lyon le 20 septembre 2022.   L'interview a été réalisée à l'occasion d'une conférence donnée le 21 septembre 2022 par Ivar Ekeland à l'attention de l'ensemble des étudiants en master de l'université Lyon 1. De nombreux personnels de l'université ont également assisté à cet exposé. Ivar Ekeland étant depuis de nombreuses années un mathématicien mobilisé sur le sujet du dérèglement climatique, nous avons souhaité d'une part en savoir plus sur sa prise de conscience individuelle, et d'autre part interroger son point de vue sur l'implication de notre communauté mathématique dans son ensemble. Sans oublier de l'inviter à nous parler de sa riche carrière de mathématicien ! Document en pdf
• 2021 : mise en place d'une UE d'enseignement transversal Climat et transitions, UE issue d'un collectif d'enseignants-chercheurs de disciplines variées, réunis par leur préoccupation et leur besoin d'action face aux enjeux du changement climatique et de l'effondrement de la biodiversité.
• Lancement fin aout 2023 d'un manifeste en collaboration avec Louis Dupaigne (Institut Camille Jordan), Anne-Laure Fougères (Institut Camille Jordan), Olivier Graf (Institut Fourier), Adeline Leclercq Samson (Laboratoire Jean Kuntzmann), Hugo Vanneuville (Institut Fourier) pour la limitation des voyages en avion dans  le milieu des mathématiciens. La manifeste a, au 22 juin 2025, obtenu plus de 650 signatures et est accéssible ICI (je vous encourage à le signer !). Environ 10% des mathématiciennes et mathématiciens de France ont signé dont 25 % de femmes, 19 % de précaires (doctorants, ATER etc. ) et 18 % de chercheuses et chercheurs. Un article sur ce sujet a été publié dans la Gazette de la SMF en janvier 2024. Document en pdf
  
• Conférence à Rennes en juin 2024, intitulée Questionnements sur la recherche mathématique : le regard d'Ivan Illich. Le texte est disponible ici en pdf. Et ces quelques pages peuvent être vues comme une sorte de pamphlet, il est question ici d'essayer modestement, de questionner notre communauté et pourquoi pas de la mettre en mouvement vers une autre façon de travailler. Si tu es lecteur de ce texte, j'attends de toi un peu de clémence et pourquoi pas une interaction future sur le sujet !
• Septembre 2024, mise en place avec Laurent Bétermin d'un magnifique groupe de travail intitiulé Explorations écologiques lien du GT.
• Septembre 2024, exposé sur les limites planétaires dans le groupe de travail Explorations écologiques, on pourra consulter les transparents ainsi qu'un document de préparation en pdf .
• Juin 2025, organisation d'une table ronde autour des impacts sociétaux des mathématique lors du congrès SMF à Dijon. Les invités étaient : Hadrien Cambazard (INP Grenoble), Adeline Leclecq Samson (Université Grenoble Alpes) et Matthieu Romagny (Montpellier).
• Juillet 2025, exposé en l'honneur de Chrstian Léonard à l'université Paris Cité, intitulé : Un héritage de Christian, l’engagement du chercheur. Voici les transparents mais aussi un texte de préparation en pdf.

Prépublications :

• L. Dupaigne, I. Gentil, S. Zugmeyer : A conformal geometric point of view on the Caffarelli-Kohn-Nirenberg inequality  Document HAL
• 
  

Publications:

• Gentil I. ; Roberto C.  Spectral gaps for spin systems: some non-convex phase examples. Journal of Functional Analysis, 180 ,no. 1, (2001) 66-84.(.ps) (.pdf)
• Bobkov S. ; Gentil I.; Ledoux M.  Hypercontractivity of Hamilton-Jacobi equations. Jounal de Mathématiques Pures et Appliquées, 80, no. 7, (2001) 669-696.(.ps) (.pdf)
• Gentil I. Ultracontractive bounds on Hamilton-Jacobi solutions. Bulletin des Sciences Mathématiques 126 (2002) 507-524.(.ps) (.pdf)
• Gentil I. ; Malrieu, F. Équations de Hamilton-Jacobi et inégalités entropiques généralisées. C. R. Acad. Sci. Paris, Ser. I 335 (2002) 437-440.(.pdf)
• Gentil I. The General Optimal $L^p$-Euclidean logarithmic Sobolev inequality by Hamilton-Jacobi equations. Journal of Functional Analysis 202, no 2, (2003) 591-599. (.pdf)
• Del Pino M. ; Dolbeault J. ; Gentil I. Nonlinear diffusions, hypercontractivity and the optimal $L^p$-Euclidean logarithmic Sobolev inequality. Journal of Mathematical Analysis and Applications 293 (2004) 375-388. (.ps)  (.pdf)
• Gentil I. ; Rémillard B. ; Del Moral P. Filtering of images for detecting multiple targets trajectories. Statistical Modeling and Analysis for Complex Data Problem (Chap 13), Kluwer Academic Publishers, (2005). (.ps)  (.pdf)  
• Gentil I. ; Guillin A. ; Miclo L. Modified logarithmic Sobolev inequalities and transportation inequalities. Probability Theory and Related Fields, 133(3), 409-436, (2005). (.ps)(.pdf)
• Dolbeault J. ; Gentil I. ; Jüngel A. A nonlinear fourth-order parabolic equation and related logarithmic Sobolev inequalities. Communications in Mathematical Sciences 4, no 2, (2006), 275-290.(.ps)(.pdf)
• Carrillo J. A. ; Dolbeault J. ; Gentil I.; Jüngel A. Entropy-Energy inequalities and improved convergence rates for nonlinear parabolic equations. Discrete and Continuous Dynamical Systems-Series B, 6 (5), 1027-1050, (2006). HAL-00008520
• Gentil I. ; Guillin A. ; Miclo L. Modified logarithmic Sobolev inequalities in null curvature. Revista Matematica Iberoamericana 23, no 1 (2007), 237-260. HAL-00016868-v2
• Cattiaux P. ; Gentil I. ; Guillin A. Weak logarithmic Sobolev inequalities and entropic convergence.  Probability Theory and related Fields, 139 (3-4), (2007), 563-603. HAL-00013700-v2
• Dolbeault J. ; Gentil I. ; Guillin A. ; Wang F.Y. L^q-functional inequalities and weighted porous media equations. Potential Analysis, 28, no 1 (2008), 35-59. HAL-00122415
• Gentil I. ; Imbert C. The Lévy-Fokker-Planck equation: Phi-entropies and convergence to equilibrium. Asymptotic Analysis, 59, no 3-4 (2008), 225-252. HAL-00113806-v2
• Gentil I. ; Rémillard B. Using systematic sampling selection for Monte Carlo solutions of Feynman-Kac equations. Advances in Applied Probability, 40, (2008), 454-572. HAL-00019334-v3
• Gentil I. From the Prékopa-Leindler inequality to modified  logarithmic Sobolev inequality. Annales de la Faculté des Sciences de Toulouse, Sér. 6, 17 no. 2 (2008), p. 291-308. HAL-00008521-v3
• Bolley F. ; Gentil I. Phi-entropy inequalities for diffusion semigroups. Jounal de Mathématiques Pures et Appliquées, 93, no. 5,(2010) 449-473. HAL-00344163-v2
• Gentil I. ; Zegarlinski B. Asymptotic behaviour of  a general reversible chemical reaction-diffusion equation.  Kinet. Relat. Models 3 (2010), no. 3, 427–444. HAL-00351445-v1
• Bakry D. ; Bolley F. ; Gentil I.; Maheux P. Weighted Nash Inequalities. Revista Matematica Iberoamericana 28 (2012), no. 3, 879–906 HAL-00474543
• Bolley F.; Gentil I.; Guillin A. : Convergence to equilibrium in Wasserstein distance for Fokker-Planck equations. Journal of Functional Analysis 263, no. 8, (2012), 2430-2457. HAL-00632941-v1
• Bakry D.; Bolley F. ; Gentil I. Dimension dependent  hypercontractivity for Gaussian kernels. Probability Theory and related Fields, 154, Issue 3 (2012), 845-874. HAL-00465879
• Bolley F.; Gentil I.; Guillin A. : Uniform convergence to equilibrium for granular media. Archive for Rational Mechanics and Analysis, 208, Issue 2 (2013), 429-445. HAL-00688780-v1
• Bolley F.; Gentil I.; Guillin A. : Dimensional contraction via Markov transportation distance. Journal of the London Mathematical Society  (2014) 90 (1): 309-332.  HAL-00808717
• Gentil I. ; Maheux P. : Nash-type inequalities, Super-Poincaré inequalities for Subordinated Semigroups. Semigroup Forum 90 (2015), no. 3, 660–693 Arxiv-1105.3095
• Gentil I.  : Dimensional contraction in Wasserstein distance for diffusion semigroups  on a Riemannian manifold. Potential Analysis Volume 42, Issue 4 (2015), Page 861-873 HAL-00873097
• Bakry D.; Gentil I.; Ledoux M. : On Harnack inequalities and optimal transportation. Annali della Scuola Normale Superiore di Pisa, Volume 14 (2015), 705-727.  HAL-00742654
• D. Bakry, F. Bolley, I. Gentil: The Li-Yau inequality and applications  under a curvature-dimension condition. Annales de l'Institut Fourier, Volume 67, 1, (2017) 397-421. HAL-01094046
• I. Gentil, C. Léonard, L. Ripani: About the analogy between optimal transport and minimal entropy. Annales de la facultés des sciences de Toulouse, Série 6, Volume 26, fascicule 3, (2017) 569-600.  HAL-01221325
• P. Fougères, I. Gentil, B. Zegarlinsli: Solution of a class of reaction-diffusion system via logarithmic Sobolev inequality. Annales Mathématiques Blaise Pascal, Vol. 24 no. 1 (2017), p. 1-53.  HAL-00987370
• F. Bolley, I. Gentil, A. Guillin, K. Kuwada: Equivalence between dimensional contractions in Wasserstein distance and the curvature-dimension condition. Annali della Scuola Normale Superiore di Pisa  Cl. Sci. (5) Vol. XVIII (2018), 1-36 HAL-01220776
• F. Bolley, I. Gentil, A. Guillin: Dimensional improvements of the logarithmic Sobolev, Talagrand and Brascamp-Lieb inequalities. Annals of probability Vol 46 (1) (2018), p. 261-301. HAL-01171361
• F. Bolley, D. Cordero, Y. Fujita, I. Gentil, A. Guillin: New sharp Gagliardo-Nirenberg-Sobolev inequalities and an improved Borell-Brascamp-Lieb inequality. IMRN, No. 10, 3042-3083 (2020). HAL-01464530
• D. Bakry, I. Gentil, G. Scheffer : Sharp Beckner-type inequalities for Cauchy and spherical distributions. Studia Mathematica (2020) 251 (3). HAL-01761215
• I. Gentil, C. Léonard, L. Ripani : Dynamical aspects of generalized Schrödinger problem via Otto calculus -- A heuristic point of view. Revista Mathematica Iberoamericana, 36, no. 4, 1071–1112 (2020). HAL-1806572
• I. Gentil, C. Léonard, L. Ripani, L. Tamanini : An entropic interpolation proof of the HWI inequality. Stochastic Processes ans their Applications, Vol. 130, Issue 2, 907-923 (2020). HAL-1840629v1
• J. Backhoff, G. Conforti, I. Gentil, C. Léonard. The mean field Schrödinger problem: ergodic behavior, entropy estimates and functional inequalities. Probability Theory and related Fields,  no. 1-2, 475–530 (2020). Document arXiv
• I. Gentil, S. Zugmeyer : A family of Beckner inequalities under various curvature-dimension conditions. Bernoulli,Vol. 27, No. 2, 751-771 (2021). Document HAL
• L. Dupaigne, I. Gentil, S. Zugmeyer : Sobolev's inequality under a curvature-dimension condition. Annales de la facultés des sciences de Toulouse,  (6) 32, No. 1, 125-144 (2023). Document HAL
• G. Clerc, G. Conforti, I. Gentil : Long-time behaviour of entropic interpolations. Potential analysis 59, No. 1, 65-95 (2023). Document HAL
• G. Clerc, G. Conforti, I. Gentil : On the variational interpretation of local logarithmic Sobolev inequalities. To appear in Annales de la facultés des sciences de Toulouse, Document HAL
• P. Cattiaux, G. Conforti, I. Gentil, C. Léonard : Time reversal of diffusion processes under a finite entropy condition. To appear in Annales de l'IHP, Document HAL
• M. Fathi, I. Gentil, J. Serres : Stability estimates for the sharp spectral gap bound under a curvature-dimension condition. To appear in  Annales de l'Institut Fourier,    Document ARXIV

• I. Gentil : L'entropie, de Clausius aux inégalités fonctionnelles La Gazette des mathématiciens 168 (avril 2021) Document HAL

• Ané C. ; Blachère S. ; Chafaï D. ; Fougères P. ; Gentil I. ; Malrieu F. ; Roberto C. ; Scheffer G.  Sur les inégalités de Sobolev logarithmiques, avec une préface de D. Bakry et M. Ledoux Panoramas et Synthèses n°10, SMF, Paris, xvi+217 (2000).
• Bakry D. ; Gentil I. ; Ledoux M.  Analysis and Geometry of Markov Diffusion operators. Springer, Grundlehren der mathematischen Wissenschaften, Vol. 348, xx+552 (2014).

• Abstract : The present volume is an extensive monograph on the analytic and geometric aspects of Markov diffusion operators. It focuses on the geometric curvature properties of the underlying structure in order to study convergence to equilibrium, spectral bounds, functional inequalities such as Poincaré, Sobolev or logarithmic Sobolev inequalities, and various bounds on solutions of evolution equations. At the same time, it covers a large class of evolution and partial differential equations.
  
  The book is intended to serve as an introduction to the subject and to be accessible for beginning and advanced scientists and non-specialists. Simultaneously, it covers a large body of results and techniques from the early developments in the mid-eighties to the latest achievements. As such, students and researchers interested in the modern aspects of Markov diffusion operators and semigroups and their connections to analytic functional inequalities, probabilistic convergence to equilibrium and geometric curvature will find it especially useful. Selected chapters can also be used for advanced courses on the topic.

• Introduction and table of contents
  
• Errata 
  
• A nice review from Thierry Coulhon
  

• Catto I. ; Gentil I. ; Pons G. :  Elements de calcul differentiel pour l'économie - Mathématiques L sciences éco - Edition Ellipses 2011. Voici la  Table des matières  et un  Extrait  

 

Proceedings :

• Gentil I.; Rémillard B. , Filtering for detecting multiple targets trajectories on a one-dimensional torus ,
  Publication du GERAD (2003) G-2003-07 (.ps),  (.pdf).
• Gentil I.; Imbert C. , Logarithmic Sobolev inequalities: regularizing effect of Lévy operators and asymptotic convergence in the Lévy-Fokker-Planck. Stochastics: An International Journal of Probability and Stochastics Processes, Vol. 81, Nos. 3–4, June–August 2009, 401–414 HAL-00321828-V1 
• Bolley F.; Gentl I.,  Phi-entropy inequalities and Fokker-Planck equations. Progress in analysis and its applications, 463–469, World Sci. Publ., Hackensack, NJ, 2010.  HAL-00459423-V1.
• Bakry D. ; Bolley F. ; Gentil I.. Around Nash Inequalities. Journées équations aux dérivées partielles (2010), Exp. No. 2, 16 p. HAL-00609026/fr/
• Gentil I. Curvature Criterion and Applications. Mathematical Notebooks Vol.3, Editor B.Zegarlinski (2011), MATRIX PRESS ltd. (.pdf).
• Gentil I. Logarithmic Sobolev inequality for diffusion semigroups. Optimal Transportation Theory and Applications, London Mathematical Society Lecture Note Series : 413, Cambridge University Press, (2014).

Note non publiée :

•  Gentil I. Inégalités de Sobolev logarithmique et de Poincaré pour la loi uniforme, Unpublished note (2004). (.ps),  (.pdf).
  

• Plutôt sur Claroline ou ailleurs.
  

• Coordonnée par Jean Dolbeault : Inégalités fonctionnelles: probabilités et EDP. (PDF)

• Dominique Bakry Université Paul Sabatier Examinateur 
• Jean Dolbeault Université Paris-Dauphine Coordinateur 
• Maria J. Esteban Université Paris-Dauphine Examinatrice
• Nassif Ghoussoub University of British Columbia Examinateur
• Alice Guionnet Ecole Normale Supérieure de Lyon Rapporteure
• Michel Ledoux Université Paul Sabatier Examinateur 
• Felix Otto Universität Bonn Rapporteur
• Laurent Saloff-Coste Cornell University Rapporteur
  

Thèse en 2001 // Ph. D. Thesis in 2001:

• Dirigée par  Michel Ledoux : Inégalités de Sobolev logarithmiques et hypercontractivité en mécanique statistique et en EDP. (PDF)
  • Dominique Bakry Université Paul Sabatier Examinateur 
  • Thierry Bodineau  Université Paris VII Examinateur 
  • Francis Comets Université Paris VII Rapporteur
  • Michel Ledoux Université Paul Sabatier Directeur
  • Laurent Miclo Université Paul-Sabatier Examinatreur
  • Jean-Michel Roquejoffre Université Paul-Sabaiter Examinateur
    
  • Cédric Villani Ecole Normale Supérieure de Lyon Rapporteur

• Luigia Ripani (2014-2017) avec Christian Léonard
  
• Simon Zugmeyer (2016-2019) avec Louis Dupaigne
  
• Gauthier Clerc (2019-2022) avec Arnaud Guillin
• Mohamed Benghazi (2021-...) avec David Lopez (Facebook) et Cédric Villani.
• Fanch Coudreuse  (2023-...) avec Filippo Santambrogio. 
  

• J.-P. Bartier (2005) examinateur
• X. Wang (2012) rapporteur
• J. Deschamp  (2013) examinateur
• N. Van Hoang (2013) examinateur
• V. Nolot (2013) examinateur
• M. Fathi (2014) examinateur
• A. Marsiglieti (2014) rapporteur
• I. Bardet ( 2016) examinateur
• Y. Shu (2016) rapporteur
• K. Tanguy (2017) examinateur
• L. Tamanini (2017) rapporteur
• B. Celaries (2019) président
  
• C. Valcu (2019) examinateur 
• A. Kroshnin (2021) président
  
• E. Bou Dagher (2022) rapporteur
  
• E. Ventre (2022) président
  
• G. Brigati (2023) rapporteur
  
• Y. Qiu (2024) rapporteur
  
• T. Caillet (2025) président