Christophe Garban's home page

My research deals mostly with Probability theory, statistical physics, discrete Fourier analysis and SLE processes. An overview of the research I have been doing up to 2013 can be found in my habilitation memoir (HDR).

Papers

The expected area of a filled planar Brownian loop is $\frac \pi 5$
with José Trujillo Ferreras
Communications in Mathematical Physics, 264 (2006), n0. 3, 797--810
[More info / Picture] [Arxiv] [Journal]

Let $B_t$ be a planar Brownian loop of time duration 1 (a Brownian motion conditioned so that $B_0 = B_1$). We consider the compact hull obtained by filling in all the holes, i.e. the complement of the unique unbounded component of $R^2 \setminus B[0,1]$. We show that the expected area of this hull is $\pi/5$. The proof uses, perhaps not surprisingly, the Schramm Loewner Evolution (SLE). Also, using the result of Yor about the law of the index of a Brownian loop, we show that the expected areas of the regions of non-zero index $n$ equal $1/(2 \pi n^2)$. As a consequence, we find that the expected area of the region of index zero inside the loop is $\pi/30$; this value could not be obtained directly using Yor's index description.

The Fourier spectrum of critical percolation
with Gábor Pete and Oded Schramm
Acta Mathematica, 205, Number 1 (2010), 19--104
[More info] [Arxiv] [Journal]

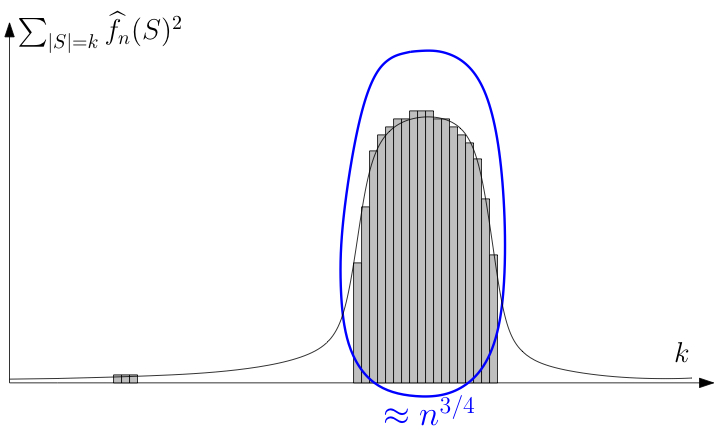
Consider the indicator function $f$ of a two-dimensional percolation crossing event. In this paper, the Fourier transform of $f$ is studied and sharp bounds are obtained for its lower tail in several situations. Various applications of these bounds are derived. In particular, we show that the set of exceptional times of dynamical critical site percolation on the triangular grid in which the origin percolates has dimension 31/36 a.s., and the corresponding dimension in the half-plane is 5/9. It is also proved that critical bond percolation on the square grid has exceptional times a.s. Also, the asymptotics of the number of sites that need to be resampled in order to significantly perturb the global percolation configuration in a large square is determined.

Continuity of the SLE trace in simply connected domains
with Steffen Rohde and Oded Schramm
Israel Journal of Mathematics, 187, No 1 (2012), 23--36
[More info] [Arxiv] [Journal]

We prove that the $SLE_\kappa$ trace in any simply connected domain $G$ is continuous (except possibly near its endpoints) if $\kappa < 8$. We also prove an SLE analog of Makarov's Theorem about the support of harmonic measure.

Oded Schramm's contributions to Noise Sensitivity
Annals of probability, 39, no 5 (2011), 1702--1767
[More info] [Arxiv] [Journal]

We survey in this paper the main contributions of Oded Schramm related to noise sensitivity. We will describe in particular his various works which focused on the "spectral analysis" of critical percolation (and more generally of Boolean functions), his work on the shape-fluctuations of first passage percolation and finally his contributions to the model of dynamical percolation.

Multi-scale bound on the four-arm event on $\mathbb{Z}^2$
Appendix to the paper "On the scaling limit of planar percolation" by Oded Schramm and Stanislav Smirnov. Annals of Probability, 39, no 5, (2011)
[Journal]
Exclusion sensitivity of Boolean functions
with Erik Broman and Jeff Steif
Probability Theory and Related Fields, 155 (2013), Issue 3-4, 621--663
[More info] [Arxiv] [Journal]

Recently the study of noise sensitivity and noise stability of Boolean functions has received considerable attention. The purpose of this paper is to extend these notions in a natural way to a different class of perturbations, namely those arising from running the symmetric exclusion process for a short amount of time. In this study, the case of monotone Boolean functions will turn out to be of particular interest. We show that for this class of functions, ordinary noise sensitivity and noise sensitivity with respect to the complete graph exclusion process are equivalent. We also show this equivalence with respect to stability.

After obtaining these fairly general results, we study "exclusion sensitivity" of critical percolation in more detail with respect to medium-range dynamics. The exclusion dynamics, due to its conservative nature, is in some sense more physical than the classical i.i.d dynamics. Interestingly, we will see that in order to obtain a precise understanding of the exclusion sensitivity of percolation, we will need to describe how typical spectral sets of percolation diffuse under the underlying exclusion process.

Lectures on noise sensitivity and percolation
with Jeff Steif
Proceedings of the Clay Mathematics Institute Summer School (Buzios, Brazil), Clay Mathematics Proceedings 15 (2012), 49--154
[Arxiv]

Pivotal, cluster and interface measures for critical planar percolation
with Gábor Pete and Oded Schramm
J. Amer. Math. Soc. 26 (2013), 939--1024
[More info] [Arxiv] [Journal]

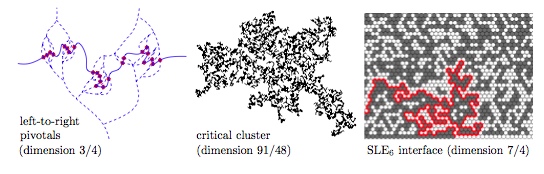
This work is the first in a series of papers devoted to the construction and study of scaling limits of dynamical and near-critical planar percolation and related objects like invasion percolation and the Minimal Spanning Tree. We show here that the counting measure on the set of pivotal points of critical site percolation on the triangular grid, normalized appropriately, has a scaling limit, which is a function of the scaling limit of the percolation configuration. We also show that this limit measure is conformally covariant, with exponent 3/4. Similar results hold for the counting measure on macroscopic open clusters (the area measure), and for the counting measure on interfaces (length measure).

Since the aforementioned processes are very much governed by pivotal sites, the construction and properties of the "local time"-like pivotal measure are key results in this project. Another application is that the existence of the limit length measure on the interface is a key step towards constructing the so-called natural time-parametrization of the SLE(6) curve.

The proofs make extensive use of coupling arguments, based on the separation of interfaces phenomenon. This is a very useful tool in planar statistical physics, on which we included a self-contained Appendix. Simple corollaries of our methods include ratio limit theorems for arm probabilities and the rotational invariance of the two-point function.

Quantum gravity and the KPZ formula
Bourbaki seminar (after Duplantier-Sheffield), Astérisque. No. 352 (2013) Exp. No. 1052. 315--354.
[More info] [Arxiv]

This text is a survey (Bourbaki seminar) on the paper "Liouville quantum gravity and KPZ" By B.Duplantier and S.Sheffield.

The study of statistical physics models in two dimensions (d=2) at their critical point is in general a significantly hard problem (not to mention the d=3 case). In the eighties, three physicists, Knizhnik, Polyakov et Zamolodchikov (KPZ) came up in \cite{\KPZ} with a novel and far-reaching approach in order to understand the critical behavior of these models. Among these, one finds for example random walks, percolation as well as the Ising model. The main underlying idea of their approach is to study these models along a two-step procedure as follows: a/ First of all, instead of considering the model on some regular lattice of the plane (such as $Z^2$ for example), one defines it instead on a well-chosen "random planar lattice". Doing so corresponds to studying the model in its {\it quantum gravity} form. In the case of percolation, the appropriate choice of random lattice matches with the so-called planar maps. b/ Then it remains to get back to the actual {\it Euclidean} setup. This is done thanks to the celebrated {\bf KPZ formula} which gives a very precise correspondence between the geometric properties of models in their quantum gravity formulation and their analogs in the Euclidean case.

The nature and the origin of such a powerful correspondence remained rather mysterious for a long time. In fact, the KPZ formula is still not rigorously established and remains a conjectural correspondence. The purpose of this survey is to explain how the recent work of Duplantier and Sheffield enables to explain some of the mystery hidden behind this KPZ formula. To summarize their contribution in one sentence, their work implies a beautiful interpretation of the KPZ correpondence through a uniformization of the random lattice, seen as a Riemann surface.

The near-critical planar FK-Ising model
with Hugo Duminil-Copin and Gábor Pete
Communications in Mathematical Physics. Volume 326 (2014), Issue 1, 1--35
[More info] [Arxiv] [Journal]

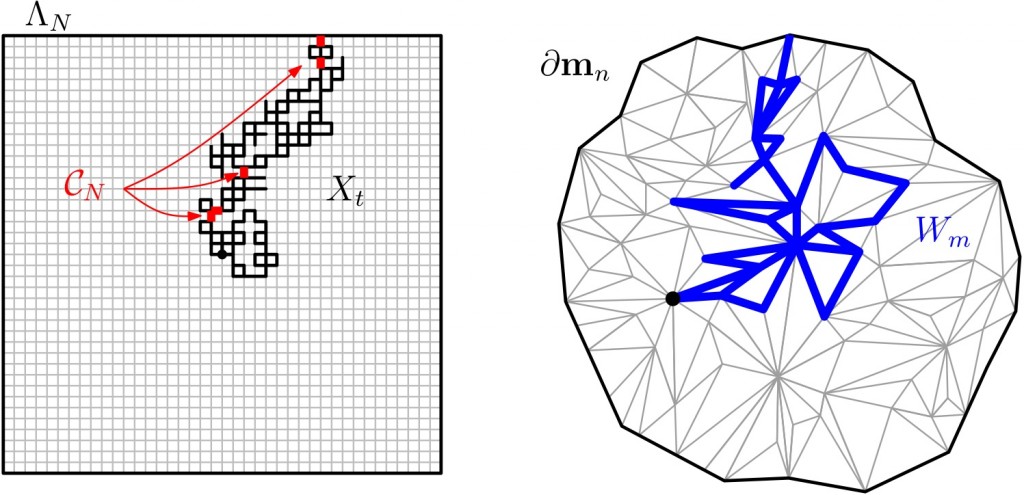
We study the near-critical FK-Ising model. First, a determination of the correlation length defined via crossing probabilities is provided. Second, a phenomenon about the near-critical behavior of FK-Ising is highlighted, which is completely missing from the case of standard percolation: in any monotone coupling of FK configurations $\omega_p$ (e.g., in the one introduced in [Gri95]), as one raises $p$ near $p_c$, the new edges arrive in a self-organized way, so that the correlation length is not governed anymore by the number of pivotal edges at criticality

The Ising magnetization exponent is $\frac{1}{15}$
with Federico Camia and Charles M. Newman
Probability Theory and Related Fields. Volume 160 (2014), Issue 1-2, 175--187
[More info] [Arxiv] [Journal]

We prove that for the Ising model defined on the plane $Z^2$ at $\beta=\beta_c$, the average magnetization under an external magnetic field $h>0$ behaves exactly like $${\sigma_0}_{\beta_c, h} \asymp h^{\frac 1 {15}}\,. $$ The proof, which is surprisingly simple compared to an analogous result for percolation (i.e. that $\theta(p)=(p-p_c)^{5/36+o(1)}$ on the triangular lattice \cite{\SmirnovWerner,\KestenScaling}) relies on the GHS inequality as well as the RSW theorem for FK percolation from \cite{\RSWfk}. The use of GHS to obtain inequalities involving critical exponents is not new; in this paper we show how it can be combined with RSW to obtain matching upper and lower bounds for the average magnetization.

Planar Ising magnetization field I. Uniqueness of the critical scaling limit
with Federico Camia and Charles M. Newman
Annals of Probability. Volume 43 (2015), Number 2, 528--571.
[More info] [Arxiv] [Journal]

The aim of this paper is to prove the following result. Consider the critical Ising model on the rescaled grid $a\, Z^2$, then the renormalized magnetization field $$\Phi^a:= a^{15/8} \, \sum_{x\in a\, Z^2} \sigma_x \delta_x,$$ seen as a random distribution (i.e., generalized function) on the plane, has a unique scaling limit as the mesh size $a\searrow 0$. The limiting field is conformally covariant.

Planar Ising magnetization field II. Properties of the critical and near-critical scaling limits
with Federico Camia and Charles M. Newman
Ann. Inst. Henri Poincaré (B) Volume 52 , Number 1 (2016), 146--161.
[More info] [Arxiv] [Journal]

In [CGN12], we proved that the renormalized critical Ising magnetization fields $\Phi^a:= a^{15/8} \sum_{x\in a\, Z^2} \sigma_x \, \delta_x$ converge as $a\to 0$ to a random distribution that we denoted by $\Phi^\infty$. The purpose of this paper is to establish some fundamental properties satisfied by this $\Phi^\infty$ and the near-critical fields $\Phi^{\infty,h}$. More precisely, we obtain the following results:
(i) If $A\subset \mathbb{C}$ is a smooth bounded domain and if $m=m_A := \langle\Phi^\infty, 1_A\rangle$ denotes the limiting rescaled magnetization in $A$, then there is a constant $c=c_A>0$ such that $$\log \mathbb{P}[m > x] \underset{x\to \infty}{\sim} -c \; x^{16}$$ In particular, this provides an alternative proof that the field $\Phi^\infty$ is non-Gaussian (another proof of this fact would use the $n$-point correlation functions established in \cite{CHI} which do not satisfy Wick's formula).
(ii) The random variable $m=m_A$ has a smooth {\it density} and one has more precisely the following bound on its Fourier transform: $|\mathbb{E}[e^{i\,t m}] |\le e^{- \tilde{c}\, |t|^{16/15}}$.
(iii) There exists a one-parameter family $\Phi^{\infty,h}$ of near-critical scaling limits for the magnetization field in the plane with vanishingly small external magnetic field.

Liouville Brownian motion
with Rémi Rhodes and Vincent Vargas
Annals of Probability. Volume 44 , Number 4 (2016), 3076-3110.
[More info] [Arxiv] [Journal]

We construct a stochastic process, called the {\bf Liouville Brownian motion}, which is the Brownian motion associated to the metric $e^{\gamma X(z)}dz^2$, $\gamma <\gamma_c=2$ and $X$ is a Gaussian Free Field. Such a process is conjectured to be the scaling limit of random walks on large planar maps eventually weighted by a model of statistical physics which are embedded in the Euclidean plane or in the sphere in a conformal manner.

The construction amounts to changing the speed of a standard two-dimensional Brownian motion $B_t$ depending on the local behaviour of the Liouville measure "$M_\gamma(dz) = e^{\gamma X(z)} dz$". We prove that the associated Markov process is a Feller diffusion for all $\gamma<\gamma_c=2$ and that for all $\gamma<\gamma_c$, the Liouville measure $M_\gamma$ is invariant under $P_t$. This Liouville Brownian motion enables us to introduce a whole set of tools of stochastic analysis in Liouville quantum gravity, which will be hopefully useful in analyzing the geometry of Liouville quantum gravity.

On the heat kernel and the Dirichlet form of Liouville Brownian Motion
with Rémi Rhodes and Vincent Vargas
Electron. J. Probab. Volume 19 (2014) 95, 1--25
[More info] [Arxiv] [Journal]

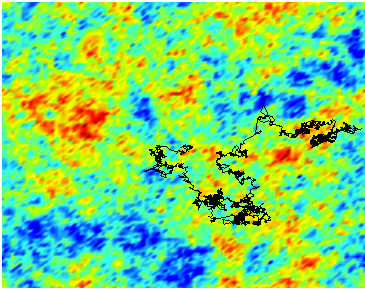
In \cite{GRV}, a Feller process called Liouville Brownian motion on $R^2$ has been introduced. It can be seen as a Brownian motion evolving in a random geometry given formally by the exponential of a (massive) Gaussian Free Field $e^{\gamma X}$ and is the right diffusion process to consider regarding 2d-Liouville quantum gravity. In this note, we discuss the construction of the associated Dirichlet form, following essentially \cite{fuku} and the techniques introduced in \cite{GRV}. Then we carry out the analysis of the Liouville resolvent. In particular, we prove that it is strong Feller, thus obtaining the existence of the Liouville heat kernel via a non-trivial theorem of Fukushima and al.

One of the motivations which led to introduce the Liouville Brownian motion in \cite{GRV} was to investigate the puzzling Liouville metric through the eyes of this new stochastic process. One possible approach was to use the theory developed for example in \cite{stollmann,sturm1,sturm2}, whose aim is to capture the "geometry" of the underlying space out of the Dirichlet form of a process living on that space. More precisely, under some mild hypothesis on the regularity of the Dirichlet form, they provide an intrinsic metric which is interpreted as an extension of Riemannian geometry applicable to non differential structures. We prove that the needed mild hypotheses are satisfied but that the associated intrinsic metric unfortunately vanishes, thus showing that renormalization theory remains out of reach of the metric aspect of Dirichlet forms.

Coalescing Brownian flows: a new approach
with Nathanael Berestycki and Arnab Sen
Annals of Probability. Volume 43 , Number 6 (2015), 3177-3215.
[More info] [Arxiv] [Journal]

The coalescing Brownian flow on $R$ is a process which was introduced by Arratia (1979) and Tóth and Werner (1997), and which formally corresponds to starting coalescing Brownian motions from every space-time point. We provide a new state space and topology for this process and obtain an invariance principle for coalescing random walks. This result holds under a finite variance assumption and is thus optimal. In previous works by Fontes et al. (2004), Newman et al. (2005), the topology and state-space required a moment of order $3-\epsilon$ for this convergence to hold. The proof relies crucially on recent work of Schramm and Smirnov on scaling limits of critical percolation in the plane. Our approach is sufficiently simple that we can handle substantially more complicated coalescing flows with little extra work -- in particular similar results are obtained in the case of coalescing Brownian motions on the Sierpinski gasket. This is the first such result where the limiting paths do not enjoy the non-crossing property.

KPZ formula derived from Liouville heat kernel
with Nathanael Berestycki , Rémi Rhodes and Vincent Vargas
Journal. of London Math. Soc. Volume 94 Number 1 (2016), 186--208.
[More info] [Arxiv] [Journal]

In this paper, we establish the Knizhnik--Polyakov--Zamolodchikov (KPZ) formula of Liouville quantum gravity, using the heat kernel of Liouville Brownian motion. This derivation of the KPZ formula was first suggested by F. David and M. Bauer in order to get a geometrically more intrinsic way of measuring the dimension of sets in Liouville quantum gravity. We also provide a careful study of the (no)-doubling behaviour of the Liouville measures in the appendix, which is of independent interest.

A dissipative random velocity field for fully developed fluid turbulence
with Laurent Chevillard and Rodrigo Pereira
Journal of Fluid Mechanics. Volume 794 (May 2016), 369--408
[More info] [Arxiv] [Journal]

We investigate the statistical properties, based on numerical simulations and analytical calculations, of a recently proposed stochastic model for the velocity field of an incompressible, homogeneous, isotropic and fully developed turbulent flow. A key step in the construction of this model is the introduction of some aspects of the vorticity stretching mechanism that governs the dynamics of fluid particles along their trajectory. An additional further phenomenological step aimed at including the long range correlated nature of turbulence makes this model depending on a single free parameter γ that can be estimated from experimental measurements. We confirm the realism of the model regarding the geometry of the velocity gradient tensor, the power-law behaviour of the moments of velocity increments (i.e. the structure functions), including the intermittent corrections, and the existence of energy transfers across scales. We quantify the dependence of these basic properties of turbulent flows on the free parameter γ and derive analytically the spectrum of exponents of the structure functions in a simplified non dissipative case. A perturbative expansion in power of γ shows that energy transfers, at leading order, indeed take place, justifying the dissipative nature of this random field.

The scaling limits of near-critical and dynamical percolation
with Gábor Pete and Oded Schramm
Journal of Eur. Math. Soc. Volume 20 , Issue 5 (2018), 1195--1268
[More info] [Arxiv] [Journal]

We prove that near-critical percolation and dynamical percolation on the triangular lattice $\eta \mathbb{T}$ have a scaling limit as the mesh $\eta \to 0$, in the "quad-crossing" space $\mathcal{H}$ of percolation configurations introduced by Schramm and Smirnov. The proof essentially proceeds by "perturbing" the scaling limit of the critical model, using the pivotal measures studied in our earlier paper. Markovianity and conformal covariance of these new limiting objects are also established.

The scaling limits of the Minimal Spanning Tree and Invasion Percolation in the plane
with Gábor Pete and Oded Schramm
Annals of Probability, Volume 46 , Number 6 (2018), 3501--3557
[More info] [Arxiv] [Journal]

We prove that the Minimal Spanning Tree and the Invasion Percolation Tree on a version of the triangular lattice in the complex plane have unique scaling limits, which are invariant under rotations, scalings, and, in the case of the MST, also under translations. However, they are not expected to be conformally invariant. We also prove some geometric properties of the limiting MST. The topology of convergence is the space of spanning trees introduced by Aizenman, Burchard, Newman & Wilson (1999), and the proof relies on the existence and conformal covariance of the scaling limit of the near-critical percolation ensemble, established in our earlier works.

Negative moments for Gaussian multiplicative chaos on fractal sets
with Nina Holden, Avelio Sepúlveda and Xin Sun
Electron. Commun. Probab. Volume 23 , paper no. 100, (2018) 10 pp.
[More info] [Arxiv] [Journal]

The objective of this note is to study the probability that the total mass of a sub-critical Gaussian multiplicative chaos (GMC) with arbitrary base measure $\sigma$ is small. When $\sigma$ has some continuous density w.r.t Lebesgue measure, a scaling argument shows that the logarithm of the total GMC mass is sub-Gaussian near $-\infty$. However, when $\sigma$ has no scaling properties, the situation is much less clear. In this paper, we prove that for any base measure $\sigma$, the total GMC mass has negative moments of all orders.

Exceptional times for percolation under exclusion dynamics
with Hugo Vanneuville
Annales scientifiques de l'École normale supérieure. Volume 52 , No 1 (2019), 1--57
[More info] [Arxiv] [Journal]

We analyse in this paper a conservative analogue of the celebrated model of dynamical percolation introduced by Häggström, Peres and Steif in [HPS97]. It is simply defined as follows: start with an initial percolation configuration $\omega(t=0)$. Let this configuration evolve in time according to a simple exclusion process with symmetric kernel $K(x,y)$. We start with a general investigation (following [HPS97]) of this dynamical process $t \mapsto \omega_K(t)$ which we call $K$-exclusion dynamical percolation. We then proceed with a detailed analysis of the planar case at the critical point (both for the triangular grid and the square lattice $Z^2$) where we consider the power-law kernels $K^\alpha$ $$ K^{\alpha}(x,y) \propto \frac 1 {\|x-y\|_2^{2+\alpha}} \, .$$ We prove that if $\alpha > 0$ is chosen small enough, there exist exceptional times $t$ for which an infinite cluster appears in $\omega_{K^{\alpha}}(t)$. (On the triangular grid, we prove that it holds for all $\alpha < \alpha_0 = \frac {217}{816}$.) The existence of such exceptional times for standard i.i.d. dynamical percolation (where sites evolve according to independent Poisson point processes) goes back to the work by Schramm-Steif in [SS10]. In order to handle such a $K$-exclusion dynamics, we push further the spectral analysis of exclusion noise sensitivity which had been initiated in [BGS13]. (The latter paper can be viewed as a conservative analogue of the seminal paper by Benjamini-Kalai-Schramm [BKS99] on i.i.d. noise sensitivity.) The case of a nearest-neighbour simple exclusion process, corresponding to the limiting case $\alpha = +\infty$, is left widely open.

On a skewed and multifractal uni-dimensional random field, as a probabilistic representation of Kolmogorov's views on turbulence
with Laurent Chevillard, Rémi Rhodes and Vincent Vargas
Ann. Henri Poincaré, Volume 20, Issue 11 (2019), pp 3693–-3741.
[More info] [Arxiv] [Journal]

We construct, for the first time to our knowledge, a one-dimensional stochastic field ${u(x)}_{x\in \mathbb{R}}$ which satisfies the following axioms which are at the core of the phenomenology of turbulence mainly due to Kolmogorov:
(i) Homogeneity and isotropy: $u(x) \overset{\mathrm{law}}= -u(x) \overset{\mathrm{law}}=u(0)$
(ii) Negative skewness (i.e. the $4/5^{th}$-law): $\mathbb{E}{(u(x+\ell)-u(x))^3} \sim_{\ell \to 0+} - C \, \ell\,,$ \, for some constant $C>0$
(iii) Intermittency: $\mathbb{E}{|u(x+\ell)-u(x) |^q} \asymp_{\ell \to 0} |\ell|^{\xi_q}\,,$ for some non-linear spectrum $q\mapsto \xi_q$
Since then, it has been a challenging problem to combine axiom (ii) with axiom (iii) (especially for Hurst indexes of interest in turbulence, namely $H<1/2$). In order to achieve simultaneously both axioms, we disturb with two ingredients a underlying fractional Gaussian field of parameter $H\approx \frac 1 3 $. The first ingredient is an independent Gaussian multiplicative chaos (GMC) of parameter $\gamma$ that mimics the intermittent, i.e. multifractal, nature of the fluctuations. The second one is a field that correlates in an intricate way the fractional component and the GMC without additional parameters, a necessary inter-dependence in order to reproduce the asymmetrical, i.e. skewed, nature of the probability laws at small scales.

On the convergence of FK-Ising Percolation to $SLE(16/3,16/3−6)$
with Hao Wu
Journal of Theoretical Probability. Volume 33, (2020) 828--865
[More info] [Arxiv] [Journal] (See also this earlier Draft of this paper which provides a different way to analyze the discrete dust.)

We give a simplified and complete proof of the convergence of the chordal exploration process in critical FK-Ising percolation to chordal SLEκ(κ−6) with κ=16/3. Our proof follows the classical excursion-construction of SLEκ(κ−6) processes in the continuum and we are thus lead to introduce suitable cut-off stopping times in order to analyse the behaviour of the driving function of the discrete system when Dobrushin boundary conditions collapse to a single point. Our proof is very different from [KS15, KS16] as it only relies on the convergence to the chordal SLEκ process in Dobrushin boundary conditions and does not require the introduction of a new observable. Still, it relies crucially on several ingredients: a) the powerful topological framework developed in [KS17] as well as its follow-up paper [CDCH+14], b) the strong RSW Theorem from [CDCH16], c) the proof is inspired from the appendix A in [BC16]. One important emphasis of this paper is to carefully write down some properties which are often considered {\em folklore} in the literature but which are only justified so far by hand-waving arguments. The main examples of these are: 1) the convergence of natural discrete stopping times to their continuous analogues. (The usual hand-waving argument destroys the spatial Markov property). 2) the fact that the discrete spatial Markov property is preserved in the the scaling limit. (The enemy being that 𝔼[Xn|Yn] does not necessarily converge to 𝔼[X|Y] when (Xn,Yn)→(X,Y)). We end the paper with a detailed sketch of the convergence to radial SLEκ(κ−6) when κ=16/3 as well as the derivation of Onsager's one-arm exponent 1/8.

Dynamical Liouville
Journal of Functional Analysis. Volume 278 , no 6, (2020) pp. 108351--108402
[More info] [Arxiv] [Journal]

The aim of this paper is to analyze an SPDE which arises naturally in the context of Liouville quantum gravity. This SPDE shares some common features with the so-called Sine-Gordon equation and is built to preserve the {\em Liouville measure} which has been constructed recently on the two-dimensional sphere $\mathbb{S}^2$ and the torus $\mathbb{T}^2$ in the work by David-Kupiainen-Rhodes-Vargas \cite{sphere, torus}. The SPDE we shall focus on has the following (simplified) form: \[ \partial_t X = \frac 1 {4\pi} \Delta X - e^{\gamma X} + \xi\,, \] where $\xi$ is a space-time white noise on $\mathbb{R}_+ \times \mathbb{S}^2$ or $\mathbb{R}_+ \times \mathbb{T}^2$. The main aspect which distinguishes this singular stochastic SPDE with well-known SPDEs studied recently (KPZ, dynamical $\Phi^4_3$, dynamical Sine-Gordon, generalized KPZ, etc.) is the presence of intermittency. One way of picturing this effect is that a naive rescaling argument suggests the above SPDE is sub-critical for all $\gamma>0$, while we don't expect solutions to exist when $\gamma > 2$. In this work, we initiate the study of this intermittent SPDE by analyzing what one might call the ``classical'' or ``Da Prato-Debussche'' phase which corresponds here to $\gamma\in[0,\gamma_{dPD}=2\sqrt{2} -\sqrt{6})$. By exploiting the positivity of the non-linearity $e^{\gamma X}$, we can push this classical threshold further and obtain this way a weaker notion of solution when $\gamma\in[\gamma_{dPD}, \gamma_{\mathrm{pos}}=2\sqrt{2} - 2)$. Our proof requires an analysis of the Besov regularity of natural space/time Gaussian multiplicative chaos (GMC) measures. Regularity Structures of arbitrary high degree should potentially give strong solutions all the way to the same threshold $\gamma_{\mathrm{pos}}$ and should not push this threshold further unless the notion of regularity is suitably adapted to the present intermittent situation. Of independent interest, we prove along the way (using techniques from \cite{sine}) a stronger convergence result for approximate GMC measures $\mu_\epsilon \to \mu$ which holds in Besov spaces.

Bargmann-Fock percolation is noise sensitive
with Hugo Vanneuville
Electr. Journal. Probab. Volume 25 , paper no. 98, (2020) 20 pp
[More info] [Arxiv] [Journal]

We show that planar Bargmann-Fock percolation is noise sensitive under the Ornstein-Ulhenbeck process. The proof is based on the randomized algorithm approach introduced by Schramm and Steif and gives quantitative polynomial bounds on the noise sensitivity of crossing events for Bargmann-Fock. A rather counter-intuitive consequence is as follows. Let $F$ be a Bargmann-Fock Gaussian field in $\mathbb{R}^3$ and consider two horizontal planes $P_1,P_2$ at small distance $\varepsilon$ from each other. Even though $F$ is a.s. analytic, the above noise sensitivity statement implies that the full restriction of $F$ to $P_1$ (i.e. $F_{| P_1}$) gives almost no information on the percolation configuration induced by $F_{|P_2}$. As an application of this noise sensitivity analysis, we provide a Schramm-Steif based proof that the near-critical window of level line percolation around $\ell_c=0$ is polynomially small. This new approach extends earlier sharp threshold results to a larger family of planar Gaussian fields.

Inverted orbits of exclusion processes, diffuse-extensive-amenability and (non-?)amenability of the interval exchanges
Groups, Geometry, and Dynamics. Volume 14, Issue 3, (2020) pp. 871--897.
[More info] [Arxiv] [Journal]

The recent breakthrough works [6,8,9] which established the amenability for new classes of groups, lead to the following question: is the action $W(\mathbb{Z}^d) \rightarrow \mathbb{Z}^d$ extensive-amenable? (Where $W(\mathbb{Z}^d)$ is the {\em wobbling group} of permutations $\sigma:\mathbb{Z}^d \to \mathbb{Z}^d$ with bounded range). This is equivalent to asking whether the action $(\mathbb{Z}/2\ \mathbb{Z})^{(\mathbb{Z}^d)} RTIMES W(\mathbb{Z}^d) \rightarrow (\mathbb{Z}/2\mathbb{Z})^{(\mathbb{Z}^d)}$ is amenable. The $d=1$ and $d=2$ and have been settled respectively in [6,8]. By [9], a positive answer to this question would imply the amenability of the IET group. In this work, we give a partial answer to this question by introducing a natural strengthening of the notion of {\em extensive-amenability} which we call {\em diffuse-extensive-amenability}. Our main result is that for any bounded degree graph $X$, the action $W(X)\rightarrow X$ is diffuse-extensive-amenable if and only if $X$ is recurrent. Our proof is based on the construction of suitable stochastic processes $(\tau_t)_{t\geq 0}$ on $W(X)\, <\, \mathfrak{S}(\mathbb{Z}^d)$ whose {\em inverted orbits} $$ \bar O_t(x_0) = \{x\in X, \exists s\leq t,\, \tau_s(x)=x_0\} = \bigcup_{0\leq s \leq t} \tau_s^{-1}(\{x_0\}) $$ are exponentially unlikely to be sub-linear when $X$ is transient. This result leads us to conjecture that the action $W(\mathbb{Z}^d) \rightarrow \mathbb{Z}^d$ is not extensive-amenable when $d\geq 3$ and that a different route towards the (non-?)amenability of the IET group may be needed.

Liouville dynamical percolation
with Nina Holden, Avelio Sepúlveda and Xin Sun
Probability Theory and Related Fields. Volume 180 , (2021) pp. 621--678
[More info] [Arxiv] [Journal]

We construct and analyze a continuum dynamical percolation process which evolves in a random environment given by a $\gamma$-Liouville measure. The homogeneous counterpart of this process describes the scaling limit of discrete dynamical percolation on the rescaled triangular lattice. Our focus here is to study the same limiting dynamics, but where the speed of microscopic updates is highly inhomogeneous in space and is driven by the $\gamma$-Liouville measure associated with a two-dimensional log-correlated field $h$. Roughly speaking, this continuum percolation process evolves very rapidly where the field $h$ is high and barely moves where the field $h$ is low. Our main results can be summarized as follows.
- First, we build this inhomogeneous dynamical percolation which we call $\gamma$-Liouville dynamical percolation (LDP) by taking the scaling limit of the associated process on the triangular lattice. We work with three different regimes each requiring different tools: $\gamma\in [0,2-\sqrt{5/2})$, $\gamma\in [2-\sqrt{5/2}, \sqrt{3/2})$, and $\gamma\in(\sqrt{3/2},2)$.
- When $\gamma<\sqrt{3/2}$, we prove that $\gamma$-LDP is mixing in the Schramm-Smirnov space as $t\to \infty$, quenched in the log-correlated field $h$. On the contrary, when $\gamma>\sqrt{3/2}$ the process is frozen in time. The ergodicity result is a crucial piece of the Cardy embedding project of the second and fourth coauthors, where LDP for $\gamma=\sqrt{1/6}$ is used to study the scaling limit of a variant of dynamical percolation on uniform triangulations.
- When $\gamma<\sqrt{3/4}$, we obtain quantitative bounds on the mixing of quad crossing events.

Statistical reconstruction of the Gaussian free field and KT transition
with Avelio Sepúlveda
Journal of Eur. Math. Soc. (to appear)
[More info] [Arxiv] [Journal]

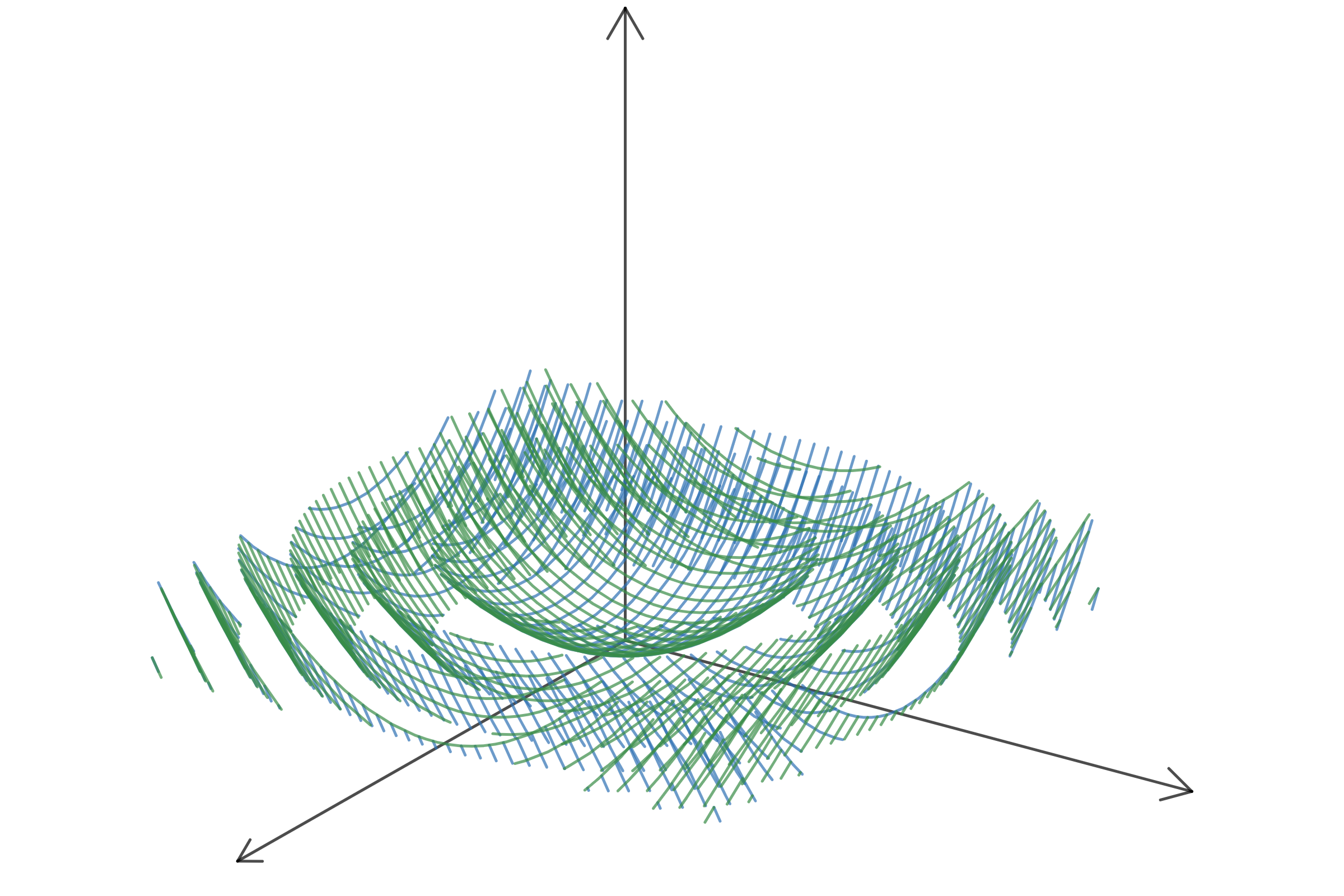
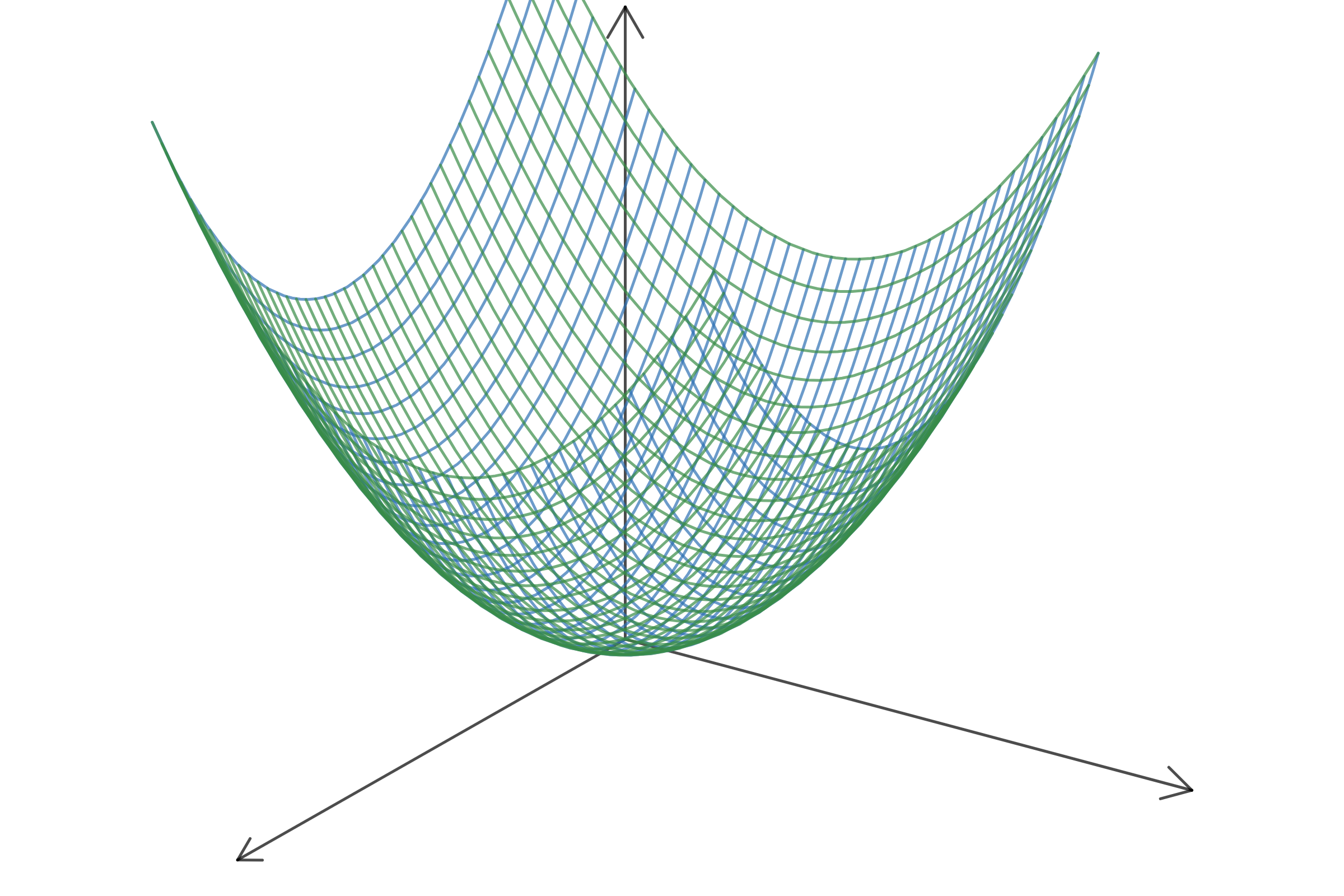
In this paper, we focus on the following question. Assume $\phi$ is a discrete Gaussian free field (GFF) on $\Lambda \subset \frac 1 n \mathbb{Z}^2$ and that we are given $e^{iT \phi}$, or equivalently $\phi \pmod{\frac {2\pi} T}$. Can we recover the macroscopic observables of $\phi$ up to $o(1)$ precision? We prove that this statistical reconstruction problem undergoes the following Kosterlitz-Thouless type phase transition:

i) If $T\leq T_{rec}^+$ one can fully recover $\phi$ from the knowledge of $\phi \pmod{\frac {2\pi} T}$. In this regime our proof relies on a new type of Peierls argument which we call {\em annealed} Peierls argument and which allows us to deal with an unknown {\em quenched} groundstate.
ii) If $T>T_{rec}^+$, it is impossible to fully recover the field $\phi$ from the knowledge of $\phi \pmod{\frac {2\pi} T}$. To prove this result, we generalise the delocalisation theorem by Fröhlich-Spencer to the case of integer-valued GFF in an inhomogeneous medium. This delocalisation result is of independent interest and an interesting connection with Riemann-theta functions is drawn along the proof.

This statistical reconstruction problem is motivated by the two-dimensional XY and Villain models. Indeed, at low-temperature $T$, the large scale fluctuations of these continuous spin systems are conjectured to be governed by a Gaussian free field. It is then natural to ask if one can recover the underlying macroscopic GFF from the observation of the spins of the XY or Villain model.
Another motivation for this work is that it provides us with an ``integrable model'' (the GFF) subjected to a KT transition.

A new proof of Liggett's theorem for non-interacting Brownian motions
with Xinxin Chen and Atul Shekhar
Electron. Commun. Probab. Volume 26 , (2021) 12 pp
[More info] [Arxiv] [Journal]

In this note, we give a new proof of Liggett's theorem on the invariant measures of independent particle systems from [Lig78] in the particular case of independent drifted Brownian motions. This particular case has received a lot of attention recently due to its applications for the analysis of the local extrema of discrete Gaussian free field. The novelty of our proof is that it identifies directly the expected Poisson Point Process with exponential intensity without relying on the Choquet-Deny convolution equation $\mu * P=\mu$ ([ChoquetDeny60,Deny60]).

Continuous symmetry breaking along the Nishimori line
with Thomas Spencer
Journal of Mathematical Physics, Volume 63 , Number 9 (2022), 093302
and
Special collection in honor of Freeman Dyson. Link to collection
[More info] [Arxiv] [Journal]

Abbe, Massoulié, Montanari, Sly and Srivastava proved in [AMM+18] that for any compact matrix Lie group G, group synchronization holds on $\mathbb{Z}^d$ when $d\geq 3$ and the ambient noise is sufficiently low. They suggest that synchronization with noisy data implies that long-range order holds for spin $O(n)$ models in a special quenched random environment called the Nishimori line. In this paper we prove continuous symmetry breaking for disordered models whose spins take values in $S^1$, $SU(n)$ or $SO(n)$ along the Nishimori line at low temperature for $d\geq 3$. The proof is based on [AMM+18] and a gauge transformation on both the disorder and the spin configurations due to Nishimori [Nis81, GHLDB85]. The proof does not use reflection positivity.

The fixed points of Branching Brownian Motion
with Xinxin Chen and Atul Shekhar
Probability Theory and Related Fields. 185 (2023), 839--884
[More info] [Arxiv] [Journal]

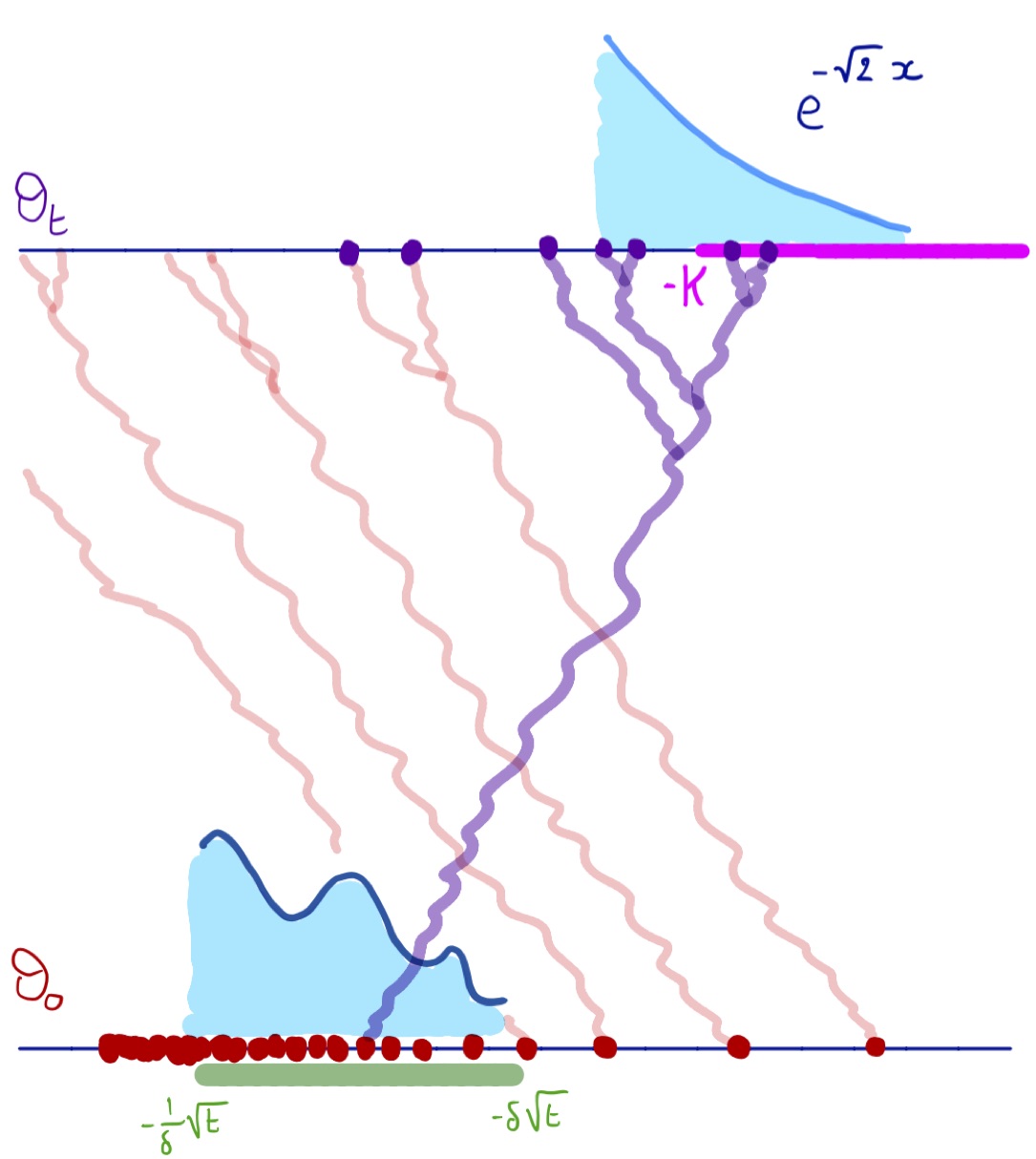
In this work, we characterize all the point processes $\theta=\sum_{i\in \mathbb{N}} \delta_{x_i}$ on $\mathbb{R}$ which are left invariant under branching Brownian motions with critical drift $-\sqrt{2}$. Our characterization holds under the only assumption that $\theta(\mathbb{R}_+)<\infty$ almost surely.

Improved spin-wave estimate for Wilson loops in U(1) lattice gauge theory
with Avelio Sepúlveda
International Mathematics Research Notices. 2023 , Issue 21 (2023), 142--198
[More info] [Arxiv] [Journal]

In this paper, we obtain bounds on the Wilson loop expectations in 4D $U(1)$ lattice gauge theory which quantify the effect of topological defects. In the case of a Villain interaction, by extending the non-perturbative technique introduced in [GS20a], we obtain the following estimate for a large loop $\gamma$ at low temperatures: \[ |\langle W_\gamma\rangle_{\beta}| \leq \exp \left(-\frac{C_{GFF}} {2\beta}(1+C \beta e^{- 2\pi^2 \beta} )(|\gamma|+o(|\gamma|)) \right)\,. \] Our result is in the line of recent works [Cha20, Cao20, FLV20, For21] which analyze the case where the gauge group is discrete. In the present case where the gauge group is continuous and Abelian, the fluctuations of the gauge field decouple into a Gaussian part, related to the so-called {\em free electromagnetic wave} [Gro83, Dri87], and a gas of {\em topological defects}. As such, our work gives new quantitative bounds on the fluctuations of the latter which complement the works by Guth and Frohlich-Spencer [Gut80, FS82]. Finally, we improve, also in a non-perturbative way, the correction term from $e^{-2\pi^2\beta}$ to $e^{-\pi^2\beta}$ in the case of the free-energy of the system. This provides a matching lower-bound with the prediction of Guth [Gut80] based on renormalization group techniques.

Long-range models in 1D revisited
with Hugo Duminil-Copin and Vincent Tassion
Ann. Inst. Henri Poincaré (B). (to appear)
[More info] [Arxiv] [Journal]

In this short note, we revisit a number of classical result{s} on long-range 1D percolation, Ising model and Potts models [FS82, NS86, ACCN88, IN88]. More precisely, we show that for Bernoulli percolation, FK percolation and Potts models, there is symmetry breaking for the $1/r^2$-interaction at large $\beta$, and that the phase transition is necessarily discontinuous. We also show, following the notation of [ACCN88] that $\beta^*(q)=1$ for all $q\geq 1$.

Quantitative bounds on vortex fluctuations in 2d Coulomb gas and maximum of the integer-valued Gaussian free field
with Avelio Sepúlveda
Proc. London Math. Soc. Volume 127 , Issue 3 (2023), 653--708
[More info] [Arxiv] [Journal]

In this paper, we study the influence of the vortices on the fluctuations of $2d$ systems such as the Coulomb gas, the Villain model or the integer-valued Gaussian free field. In the case of the $2d$ Villain model, we prove that the fluctuations induced by the vortices are at least of the same order of magnitude as the ones produced by the spin-wave. We obtain the following quantitative upper-bound on the two-point correlation in $\mathbb{Z}^2$ when $β>1$ $$ \langleσ_x σ_y\rangle_β^{Villain} \leq C \, \left( \frac 1 {\|x-y\|_2}\right)^{\frac 1 {2πβ}\left ( 1+β e^{-\frac{(2π)^2}{2} β}\right )} $$ The proof is non-perturbative and relies on a new way of sampling the $2d$ Coulomb gas. For the $2d$ Coulomb gas, we obtain the following lower bound on its fluctuations at high inverse temperature $$ \mathbb{E}_β^{Coul}\left[\langle Δ^{-1}q, g\rangle \right] \geq \exp(-π^2 β+ o(β)) \langle g,(-Δ)^{-1}g\rangle $$ This estimate coincides with the predictions based on a RG analysis from \cite{Kadanoff} and suggests that the Coulomb potential $Δ^{-1}q$ at inverse temperature $β$ should scale like a Gaussian free field of inverse temperature of order $\exp(π^2 β)$. Finally, we transfer the above vortex fluctuations via a duality identity to the integer-valued GFF by showing that its maximum deviates in a quantitative way from the maximum of a usual GFF. More precisely, we show that with high probability when $β>1$ $$ \max_{x\in [-n,n]^2} ϕ_n^{IV} \leq \sqrt{\frac{2β}π \big(1 - βe^{- \frac{(2π)^2β} {2} } \big)} \log n \,. $$ where $ϕ_n$ is an integer-valued GFF in the box $[-n,n]^2$ at inverse temperature $β^{-1}$. Applications to the free-energies of the Coulomb gas, the Villain model and the integer-valued GFF are also considered.

Long-range order for critical Book-Ising and Book-percolation
with Hugo Duminil-Copin and Vincent Tassion
Communications in Mathematical Physics. (to appear)
[More info] [Arxiv]

In this paper, we investigate the behaviour of statistical physics models on a book with pages that are isomorphic to half-planes. We show that even for models undergoing a continuous phase transition on $\mathbb Z^2$, the phase transition becomes discontinuous as soon as the number of pages is sufficiently large. In particular, we prove that the Ising model on a three pages book has a discontinuous phase transition (if one allows oneself to consider large coupling constants along the line on which pages are glued).
Our work confirms predictions in theoretical physics which relied on renormalization group, conformal field theory and numerics ([Car91,ITB91,SMP10]) some of which were motivated by the analysis of the Renyi entropy of certain quantum spin systems.

Superconcentration for minimal surfaces in first passage percolation and disordered Ising ferromagnets
with Barbara Dembin
Probability Theory and Related Fields. (to appear)
[More info] [Arxiv]

We consider the standard first passage percolation model on $\mathbb{Z}^d$ with a distribution $G$ taking two values $0<a<b$. We study the maximal flow through the cylinder $[0,n]^ {d-1}\times [0,hn]$ between its top and bottom as well as its associated minimal surface(s). We prove that the variance of the maximal flow is superconcentrated, i.e. in $O(\frac {n^{d-1}} {\log n})$, for $h\geq h_0$ (for a large enough constant $h_0=h_0(a,b)$). Equivalently, we obtain that the ground state energy of a disordered Ising ferromagnet in a cylinder $[0,n]^ {d-1}\times [0,hn]$ is superconcentrated when opposite boundary conditions are applied at the top and bottom faces and for a large enough constant $h\geq h_0$ (which depends on the law of the coupling constants). Our proof is inspired by the proof of Benjamini--Kalai--Schramm. Yet, one major difficulty in this setting is to control the influence of the edges since the averaging trick used in the proof of Benjamini--Kalai--Schramm fails for surfaces. Of independent interest, we prove that minimal surfaces (in the present discrete setting) cannot have long thin chimneys.

Preprints

Percolation for 2D classical Heisenberg model and exit sets of vector valued GFF
with Juhan Aru and Avelio Sepúlveda
[More info] [Arxiv]

Our motivation in this paper is twofold. First, we study the geometry of a class of exploration sets, called exit sets, which are naturally associated with a 2D vector-valued GFF : $\phi : Z^2 \to R^N, N\geq 1$. We prove that, somewhat surprisingly, these sets are a.s. degenerate as long as $N\geq 2$, while they are conjectured to be macroscopic and fractal when $N=1$. This analysis allows us, whe $N\geq 2$, to understand the percolation properties of the level sets of $\{\|\phi(x)\|, x\in Z^2\}$ and leads us to our second main motivation in this work: if one projects a spin $O(N+1)$ model (classical Heisenberg model is $N=2$) down to a spin $O(N)$ model, we end up with a spin $O(N)$ in a quenched disorder given by random conductances on $Z^2$. Using the exit sets of the $N$-vector-valued GFF, we obtain a local and geometric description of this random disorder in the limit $\beta\to \infty$. This allows us to revisit a series of celebrated works by Patrascioiu and Seiler ([PS92, PS93, PS02]) which argued against Polyakov's prediction that spin $O(N+1)$ model is massive at all temperatures when $N\geq 2$ ([Pol75]). We make part of their arguments rigorous and more importantly we provide the following counter-example: we build ergodic environments of (arbitrary) high conductances with (arbitrary) small and disconnected regions of low conductances in which, despite the predominance of high conductances, the $XY$ model remains massive.

Of independent interest, we prove that at high $\beta$, the transverse fluctuations of a classical Heisenberg model are given by a $N=2$ vectorial GFF. This is implicit in [Pol75] but we give here the first (non-trivial) rigorous proof. Also, independently of the recent work [DF22], we show that two-point correlation functions of the spin $O(N)$ model are given in terms of certain percolation events in the cable graph for any $N\geq 1$.

Domain of attraction of the fixed points of Branching Brownian motion
with Xinxin Chen and Atul Shekhar
[More info] [Arxiv]

We give a complete characterisation of the domain of attraction of fixed points of branching Brownian motion (BBM) with critical drift. Prior to this classification, we introduce a suitable metric space of locally finite point measures on which we prove 1) that the BBM with critical drift is a well-defined Markov process and 2) that it satisfies the Feller property. Several applications of this characterisation are given.

Harmonic analysis of Gaussian multiplicative chaos on the circle
with Vincent Vargas
[More info] [Arxiv]

In this paper, we initiate the harmonic analysis of Gaussian multiplicative chaos (GMC) on the circle, i.e. the study of its Fourier coefficients. In particular, we show that almost surely GMC is a so-called Rajchman measure which means that its Fourier coefficients converge to 0 when the frequency goes to infinity. We supplement this result with a convergence in law result for the rescaled Fourier coefficient (for small values of the parameter underlying the GMC theory).

Phase transitions for the XY model in non-uniformly elliptic and Poisson-Voronoi environments
with Paul Dario
[More info] [Arxiv]

The goal of this paper is to analyze how the celebrated phase transitions of the $XY$ model are affected by the presence of a non-elliptic quenched disorder.
In dimension $d=2$, we prove that if one considers an $XY$ model on the infinite cluster of a supercritical percolation configuration, the Berezinskii-Kosterlitz-Thouless (BKT) phase transition still occurs despite the presence of quenched disorder. The proof works for all $p>p_c$ (site or edge). We also show that the $XY$ model defined on a planar Poisson-Voronoi graph also undergoes a BKT phase transition.
When $d\geq 3$, we show in a similar fashion that the continuous symmetry breaking of the $XY$ model at low enough temperature is not affected by the presence of quenched disorder such as supercritical percolation (in $\mathbb{Z}^d$) or Poisson-Voronoi (in $\mathbb{R}^d$).
Adapting either Fröhlich-Spencer's proof of existence of a BKT phase transition or the more recent proofs of Lammers, van Engelenburg-Lis and Aizenman-Harel-Peled-Shapiro to such non-uniformly elliptic disorders appears to be non-trivial. Instead, our proofs rely on a relatively little known correlation inequality called Wells' inequality.

Invisibility of the integers for the discrete Gaussian chain via a Caffarelli-Silvestre extension of the discrete fractional Laplacian
[More info] [Arxiv]

The Discrete Gaussian Chain is a model of interfaces $\Psi : \mathbf{Z} \to \mathbf{Z}$ governed by the Hamiltonian $$ H(\Psi)= \sum_{i\neq j} J_\alpha(|i-j|) |\Psi_i -\Psi_j|^2 $$ with long-range coupling constants $J_\alpha(k)\asymp k^{-\alpha}$. For any $\alpha\in [2,3)$ and at high enough temperature, we prove an invariance principle for such an $\alpha$-Discrete Gaussian Chain towards a $H(\alpha)$-fractional Gaussian process where the Hurst index $H$ satisfies $H=H(\alpha)=\frac {\alpha-2} 2$.
This result goes beyond a conjecture by Fröhlich and Zegarlinski \cite{frohlich1991phase} which conjectured fluctuations of order $n^{\tfrac 1 2 (\alpha-2) \wedge 1}$ for the Discrete Gaussian Chain.
More surprisingly, as opposed to the case of $2D$ Discrete Gaussian $\Psi : \mathbf{Z}^2 \to \mathbf{Z}$, we prove that the integers do not affect the {\em effective temperature} of the discrete Gaussian Chain at large scales. Such an {\em invisibility of the integers} had been predicted by Slurink and Hilhorst in the special case $\alpha_c=2$ in \cite{slurink1983roughening}.
Our proof relies on four main ingredients: (1) A Caffareli-Silvestre extension for the discrete fractional Laplacian (which may be of independent interest) (2) A localisation of the chain in a smoother sub-domain (3) A Coulomb gas-type expansion in the spirit of Fröhlich-Spencer \cite{FS} (4) Controlling the amount of Dirichlet Energy supported by a $1D$ band for the Green functions of $\mathbf{Z}^2$ Bessel type random walks
Our results also have implications for the so-called {\em Boundary Sine-Gordon field}. Finally, we analyse the (easier) regimes where $\alpha\in(1,2) \cup (3,\infty)$ as well as the $2D$ Discrete Gaussian with long-range coupling constants (for any $\alpha>\alpha_c=4$).

Villain action in lattice gauge theory
with Ilya Chevyrev
[More info] [Arxiv]

We prove that Villain interaction applied to lattice gauge theory can be obtained as the limit of both Wilson and Manton interactions on a larger graph which we call the {\em carpet graph.} This is the lattice gauge theory analog of a well-known property for spin $O(N)$ models where Villain type interactions are the limit of $\mathbb{S}^{N-1}$ spin systems defined on a {\em cable graph}.
Perhaps surprisingly in the setting of lattice gauge theory, our proof also applies to non-Abelian lattice theory such as $SU(3)$-lattice gauge theory and its limiting Villain interaction.
In the particular case of an Abelian lattice gauge theory, this allows us to extend the validity of Ginibre inequality to the case of the Villain interaction.

PhD and HDR memoirs

Manuscript of my PhD thesis (December, 5th 2008) : link to file
Manuscript of my Habilitation (HDR) (December, 9th 2013) : link to file

Coauthors

Juhan Aru, Nathanael Berestycki, Erik Broman, Federico Camia, Xinxin Chen, Ilya Chevyrev, Barbara Dembin, Paul Dario, Hugo Duminil-Copin, Laurent Chevillard, Nina Holden, Charles M. Newman, Rodrigo Pereira, Gábor Pete, José Trujillo Ferreras, Rémi Rhodes, Steffen Rohde, Oded Schramm, Arnab Sen , Avelio Sepúlveda, Atul Shekhar, Thomas Spencer , Jeff Steif, Xin Sun, Vincent Tassion, Hugo Vanneuville, Vincent Vargas, Hao Wu