Il y a deux sujets. Le « vrai » sujet porte sur la répartition asymptotique des racines des troncatures du développement de Taylor de l’exponentielle. Mais il a été proposé comme devoir pendant les vacances de Noël 2010-2011. Ceux qui l’auraient déjà étudié (et seulement eux, slp), pourront se rabattre sur l’autre sujet.
Addendum 12 h 40
Voici, pour étayer le préambule, quelques représentations des zéros des 57 premiers polynômes $P_n(x)=\sum_{k=0}^nx^k/k!$.
La couleur du point dépend de l’indice $n$ dont il est un zéro : du vert pour les petites valeurs de $n$ vers le rouge pour les plus grandes valeurs.
Voici un premier dessin des zéros de $P_n$, les $\lambda_{n,k}$ ($1\le n\le 57$, $1\le k\le n$) (cliquer pour agrandir l’image) :
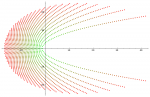
On normalise, c’est-à-dire qu’on représente les $z_{n,k}=\lambda_{n,k}/n$ ($1\le n\le 57$) :
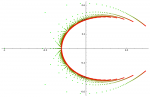
Voici les $\xi_{n,k}=z_{n,k}\exp(-z_{n,k})$ ($1\le n\le 57$) :
Zoom :
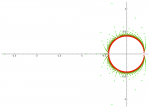
Addendum 13 h 40 : correction
- Un corrigé du problème de Centrale 2001
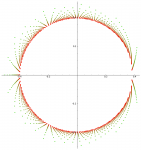
Commentaires