Rien que des carrés : explication de la figure
Relations entre les côtés des différents carrés
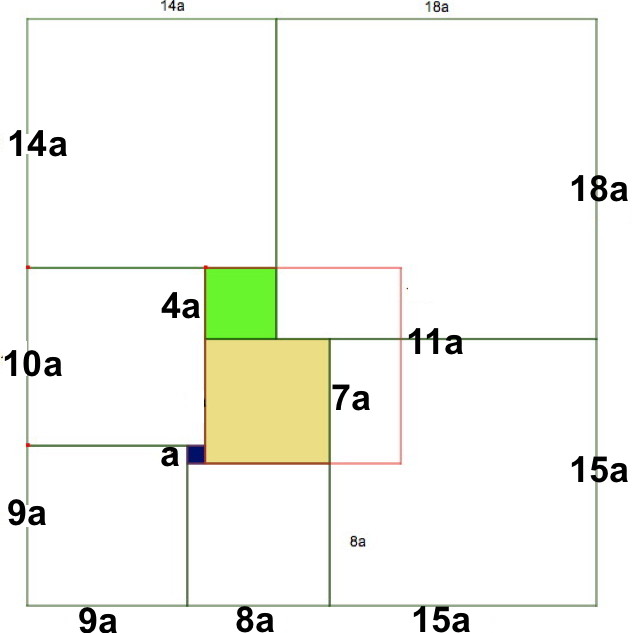La connaissance de la longueur d’un des carrés suffit à calculer toutes les autres (Voir démonstration ci-dessous).
Connaissant deux longueurs, c’est plus facile, mais il reste tout de même du travail !
On a choisi de donner a et 10a (avec a=1).
On pourrait donner aussi les longueurs a et 9a ou a et 7a .
Une stratégie possible : reproduire la figure sur une feuille à petits carreaux.
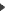
- Démonstration
| I Une spirale
Pour simplifier, posons a =1. On peut observer trois carrés construits en spirale à partir du carré de côté x (en jaune). Ces carrés ont respectivement pour côtés |
II Une autre spirale
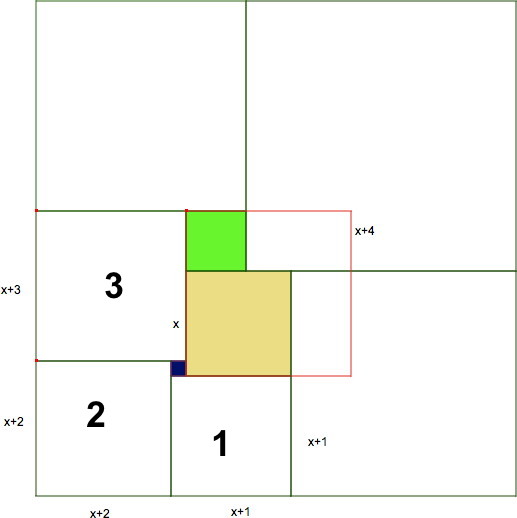
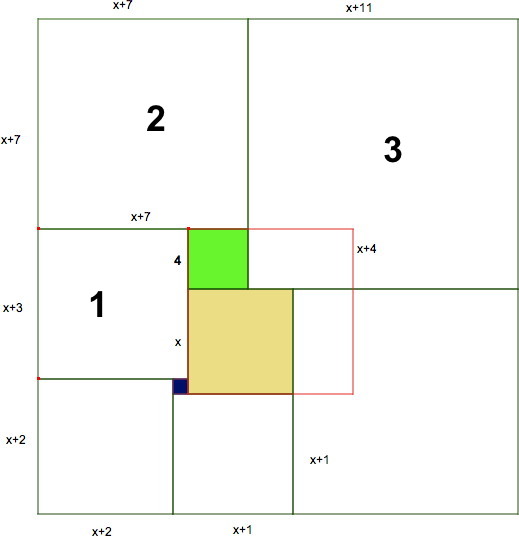
Autour du carré vert, de côté 4, il y a un autre début de spirale, commençant au carré de côté x +4. Cela nous donne les dimensions des deux grands carrés en haut : x +7 et x +11. |
|
|
| III En comparant les deux largeurs du rectangle, on calcule le côté du dernier carré : 15. On peut aussi exprimer cette longueur en fonction de x : x + 1 + x = 2x + 1. On en déduit 2x + 1 = 15 et x = 7. | |
Commentaires