MathC2+
Au bâtiment Nautibus, rue André-Marie Ampère, 69622 Villeurbanne cedex, salle C5, à l’Université Claude Bernard Lyon 1.
| Mardi 25 juin | Mercredi 26 juin | Jeudi 27 juin | ||
|---|---|---|---|---|
| 9h30-11h | Vincent Borrelli Math : silence on tourne ! | 8h30-10h | Simon Masnou Chirurgie mathématique d’une image numérique | Anne Perrut Mathe les couleurs |
| 11h15-12h45 | Plaisir Math Projet Rebond | 10h15-11h45 | Plaisir Math Projet Rebond | Plaisir Math Projet Rebond |
| 13h-14h15 | Repas (Jussieu) | 12h-13h | Repas (Jussieu) | Repas (Jussieu) |
| 14h15-15h45 | Pierre Gallais L’art de la mathologie | 13h-17h15 | Plaisir Math Rallye | 13h-14h30 Bodo Lass Résoudre des problèmes |
| 16h-17h30 | Régis Goiffon MathαLyon | Institut Lumière | 14h45-16h15 Plaisir Math Les mathématiques du cinéma | |
| 17h15-19h | Plaisir Math Pique-nique Lumière | |||
| 20h-22h | Plaisir Math Veillée cinéma, lycée Lamartinière (pour les "internes") |
Vincent Borrelli a expliqué la polémique sur le galop du cheval et du premier film scientifique par Eadweard Muybridge, pour enchaîner sur les systèmes dynamiques, le système solaire et l’effet papillon.
Pierre Gallais vous a mis à l’ouvrage autour de certaines de ses œuvres sur la perspective par une réalisation artistique et mathématique.
Régis Goiffon a animé l’atelier Math@Lyon d’activités mathématiques.
Simon Masnou a défini ce qu’est une image numérique et comment on peut la modifier, la comprimer ou l’améliorer.
Anne Perrut a décrit une courbe omniprésente dans les phénomènes naturels, commune à une impression colorée, un tour de prestidigitation et un mensonge dans les sondages : la courbe de Gauss, des statistiques, des moyennes et des écart-type.
Bodo Lass (sur un travail conjoint avec Theresia Eisenkoelbl) a présenté la géométrie projective, qui est la géométrie du cinéma, où des droites de l’espace sont projetées sur un point du plan, comment on calcule avec cette géométrie et en quoi elle peut vous aider à résoudre des problèmes.

- La trajectoire
Dans le projet rebond, vous avez analysé image par image un film sur le rebond d’une bille. Le mouvement étant capté , les calculatrices Casio Graph 35+ permettent de tabuler et tracer le résultat, d’en décortiquer la construction jusqu’à une modélisation permettant de simuler le phénomène sur l’écran, premier pas d’un film d’animation (voir plus bas).

- Programme Python SimpleCV
- Utilise la bibliothèque SimpleCV
Le logiciel de récupération de données est attaché, il faut installer SimpleCV pour le faire fonctionner. C’est un peu technique. Vous pouvez aussi simplement utiliser nos jeux de données.
Programme Casio
Les données tirées de quatre films ont été tabulées dans un fichier CSV, qui peut être importé par le programme ProgramLink© FA-124. Les copies d’écran supposent que vous mettez ce fichier dans les données File 5. Les programmes et données peuvent également être importées, il suffit de télécharger ce fichier, de l’ouvrir avec FA-124 et de le déposer sur la calculatrice branchée par USB.

- Menu STAT

- Sélection des données File 5
Sélectionnez ces données (STAT, SHIFT SET UP, File 5, EXE).
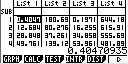
- Les données
- Chaque paire de colonnes contient les données (x,y) de chaque échantillon, List 1 et List 2 par exemple sont les données tabulées du premier échantillon, List 7 et List 8 le quatrième.
Ces données peuvent être visualisées (GRPH) et analysées. Comme ces données comprennent plusieurs rebonds, pour pouvoir les comprendre, il faut tout d’abord les séparer.
- Le menu programme

- Lancement du programme PARABSEL
Le programme PARABSEL va permettre de sélectionner chaque parabole et les mettre dans une liste séparée.

- L’exécution de PARABSEL
- Choisissez le numéro des listes X et Y à analyser, par exemple 1 et 2, puis le numéro de la parabole à sélectionner, par exemple 2. Ensuite, donnez les numéros des listes où ces données seront stockées, par exemple 9 et 10.
Ce programme utilise quatre sous-programmes, AVMAX, AVMIN, RECMAX et RECMIN qui se ressemblent. Leur but est d’avancer un compteur jusqu’au prochain maximum d’une liste donnée, ou son minimum, et de recopier ou non ces données dans une autre liste. Si par exemple on désire recopier dans les listes 9 et 10 les données du jeu de données des listes 1 et 2, correspondant à la troisième parabole, il faut indiquer ces paramètres à l’exécution.
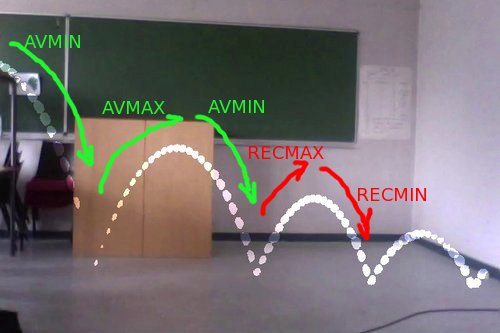
- PARABSEL appelle AVMAX, AVMIN, RECMAX, RECMIN

- Enlever les zéros
Malheureusement, la taille des données n’est pas connue à l’avance (il faudrait exécuter deux fois le passage pour celà, modifiez le programme en conséquence !), il y a donc des données parasite (0,0) à effacer, et les premières et dernières données sont peut-être à rapprocher à la parabole précédente ou la suivante, que l’analyse attentive permet de déterminer.
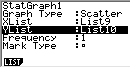
- Sélection des listes à visualiser

- StatGraph1
Sélectionnez les données à visualiser (SEL, GRPH1, puis List 9 et List 10) et analyser (CALC, X^2, DRAW). Vous pouvez également copier et coller le trinôme du second degré dans la bibliothèque de fonctions. De cette manière vous pouvez visualiser les fonctions associées à chaque parabole et étudier la suite des paramètres.
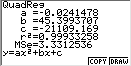
- Régression quadratique X^2

- Graphe associé à la régression quadratique
L’altitude des sommets compose ainsi une suite géométrique tandis que leur abscisse est plus compliquée, mais facile à explorer dans le tableur de geogebra (la vitesse horizontale est constante, il suffit de calculer le temps entre deux rebonds).
Il est à noter ici que, dans la réalité, le nombre de rebonds est forcément fini. Qu’en est-il dans notre modèle ? Le nombre de rebonds est infini, mais, comme dans le monde réel, le temps de rebonds est fini : le temps de rebond est à chaque fois une fraction constante du temps précédent, le temps total en étant la somme, qui converge. Si bien que les sommets des paraboles convergent donc, puis la bille roule sans plus rebondir. C’est tout à fait étonnant à première vue mais on peut s’en approcher avec une bille d’acier sur du marbre, pour un choc quasi élastique, on reconnait bien le bruit des tac-tac de plus en plus rapprochés jusqu’à s’arrêter sur un son aigu.




Commentaires