1- Qu’est-ce qu’un calendrier ?
![]() Étude du regroupement des jours
Étude du regroupement des jours
![]() On suppose les jours égaux.
On suppose les jours égaux.

- Le Soleil le matin depuis l’observatoire de Crimée
![]() Quand débute le jour ?
Quand débute le jour ?
- au coucher du Soleil : Juifs, Musulmans, Grecs anciens, Chinois,…
- au lever du Soleil : Chaldéens, Égyptiens, Perses, Syriens, Grecs modernes…
- à midi (passage au méridien) : Arabes anciens, astronomes,…
- à minuit : Astronomes anciens, Européens,…
2- Compter les jours
![]() Pas facile : 50 ans = 18000 jours. Difficile à écrire (par exemple en chiffres romains).
Pas facile : 50 ans = 18000 jours. Difficile à écrire (par exemple en chiffres romains).
![]() Mais grande précision.
Mais grande précision.
![]() Choix du début du jour (nycthémère).
Choix du début du jour (nycthémère).
![]() Permet de comparer les calendriers des différents peuples.
Permet de comparer les calendriers des différents peuples.
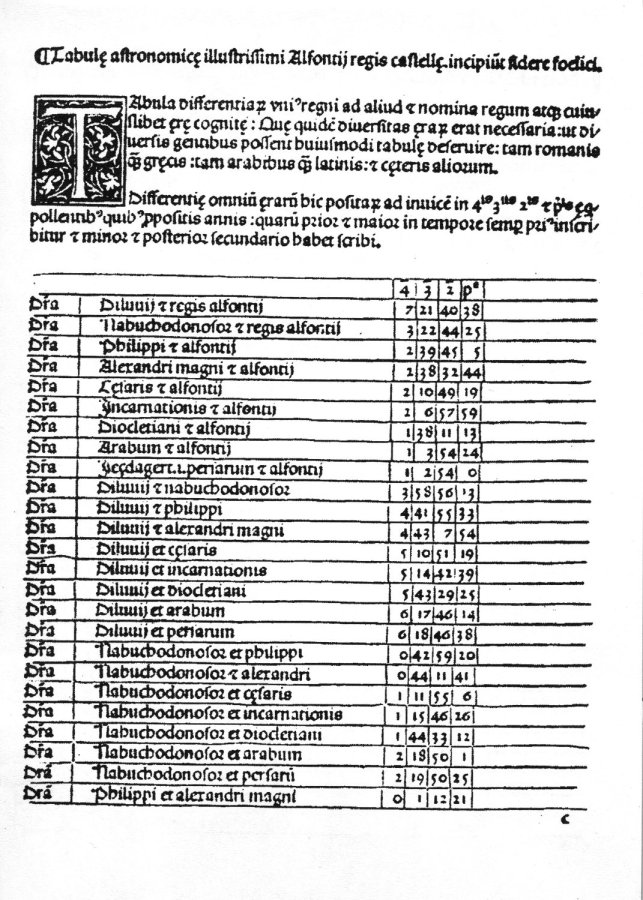
- Table alphonsine
![]() La base 60 et autres bases : Passage d’une base à l’autre
La base 60 et autres bases : Passage d’une base à l’autre
![]() On trouve (5ème ligne : différence entre l’incarnation et le Roi Alphonse) : 2/6/57/59 = 59 + 57 × 60 + 6 × 602 + 2 × 603 = 457 079 : quelle date pour le couronnement ?
On trouve (5ème ligne : différence entre l’incarnation et le Roi Alphonse) : 2/6/57/59 = 59 + 57 × 60 + 6 × 602 + 2 × 603 = 457 079 : quelle date pour le couronnement ?
![]() De même (8ème ligne : différence entre les Arabes, c’est-à-dire l’Hégire, et le Roi Alphonse) : 1/3/54/14 = 14 + 54 × 60 + 3 × 602 + 1 × 603 = 230 054 (15 juillet 622 ou plutôt le 22 septembre 622)
De même (8ème ligne : différence entre les Arabes, c’est-à-dire l’Hégire, et le Roi Alphonse) : 1/3/54/14 = 14 + 54 × 60 + 3 × 602 + 1 × 603 = 230 054 (15 juillet 622 ou plutôt le 22 septembre 622)
![]() Le siècle julien = 365×100+25=36525 jours est le multiple classique
Le siècle julien = 365×100+25=36525 jours est le multiple classique
![]() Il faut donc regrouper par paquets : 5, 7, 8, 10, 20, 30, 60…
Il faut donc regrouper par paquets : 5, 7, 8, 10, 20, 30, 60…
![]() Par exemple par 7, cela conduit à la semaine. Quel est le premier jour de la semaine ?
Par exemple par 7, cela conduit à la semaine. Quel est le premier jour de la semaine ?
Mais pourquoi cet ordre des jours de la semaine en français (espagnol, anglais, allemand…) ?

- Calendrier des bergers
![]() L’ordre provient de l’ordre attribué aux "planètes" selon la tradition et qui correspond au temps de parcours dans le ciel.
L’ordre provient de l’ordre attribué aux "planètes" selon la tradition et qui correspond au temps de parcours dans le ciel.
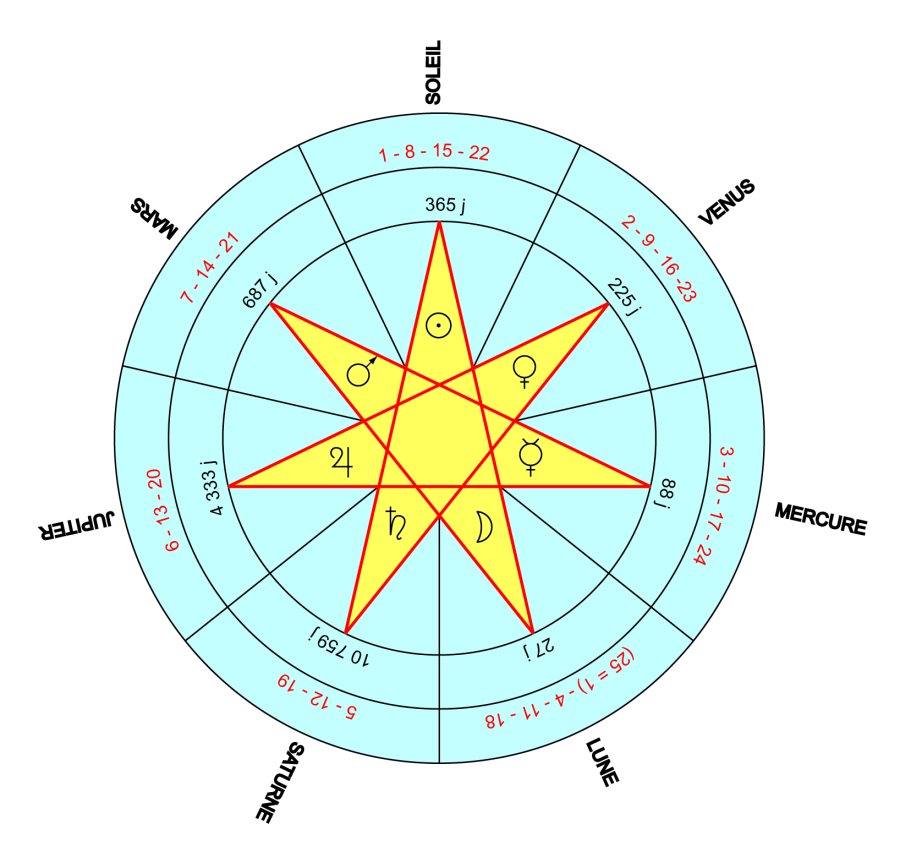
- Ordre des jours
![]() La semaine nous oblige à calculer modulo 7. Quel jour était le 13 mai 1968 (il y a 40 ans) ?
La semaine nous oblige à calculer modulo 7. Quel jour était le 13 mai 1968 (il y a 40 ans) ?
3- Les mois
![]() Si l’alternance des jours est un phénomène marquant, d’autres phénomènes astronomiques sont bien visibles : Le mouvement de la Lune ou du Soleil
Si l’alternance des jours est un phénomène marquant, d’autres phénomènes astronomiques sont bien visibles : Le mouvement de la Lune ou du Soleil
![]() Le mois lunaire = lunaison = retour des mêmes phases. Pas régulier.
Le mois lunaire = lunaison = retour des mêmes phases. Pas régulier.
![]() Moyenne (29,530588 j = 29 j 12 h 44 min 3s) ne tombe pas juste.
Moyenne (29,530588 j = 29 j 12 h 44 min 3s) ne tombe pas juste.
![]() Sauf à changer de mois à n’importe quel moment on alterne, en première approximation 29 et 30 j. Mais 45 min donne une journée en 32 mois.
Sauf à changer de mois à n’importe quel moment on alterne, en première approximation 29 et 30 j. Mais 45 min donne une journée en 32 mois.
![]() Choix du début du mois : Nouvelle Lune (mais on ne voit rien d’où décalage de 2 jours environ), Nouvelle Lune ou quartier (un peu plus précis, mais difficile à évaluer) et si temps couvert que fait-on ?
Choix du début du mois : Nouvelle Lune (mais on ne voit rien d’où décalage de 2 jours environ), Nouvelle Lune ou quartier (un peu plus précis, mais difficile à évaluer) et si temps couvert que fait-on ?
![]() Linguistique : mois = mesure mais dans d’autres langues mois = lune (anglais, allemand, guarani, chinois,…). Lune du latin luna = leuk-sna = la lumineuse.
Linguistique : mois = mesure mais dans d’autres langues mois = lune (anglais, allemand, guarani, chinois,…). Lune du latin luna = leuk-sna = la lumineuse.
![]() Nécessité de regrouper les mois. Dans les zones linguistiques de base dix, on les regroupe par 10 (latin, arabe), souvent numérotés.
Nécessité de regrouper les mois. Dans les zones linguistiques de base dix, on les regroupe par 10 (latin, arabe), souvent numérotés.
| Exemple arabe | Muharram | Safar | Rabia I | Rabi II |
| Jumada I | Jumada II | Rajab | Sha’aban | |
| Ramadan | Shawwal | Dhulqa’da | Dhul-hijja | |
| Exemple latin | Martius | Aprilis | Maius | Junius |
| Quintilis | Sextilis | September | October | |
| November | December | (Januarus) | (Februarus) |
![]() Mais aussi influence de l’année tropique, année des saisons, d’où instabilité et regroupement par 12. Mais 12 lunaisons environ 354,367056 jours. Manquent 11 jours.
Mais aussi influence de l’année tropique, année des saisons, d’où instabilité et regroupement par 12. Mais 12 lunaisons environ 354,367056 jours. Manquent 11 jours.
![]() Une nouvelle façon d’additionner les fractions.
Une nouvelle façon d’additionner les fractions.
![]() Nul besoin de construire toute la liste pour trouver de bonnes approximations rationnelles.
Nul besoin de construire toute la liste pour trouver de bonnes approximations rationnelles.
On va appliquer cela à l’année lunaire de 354,367056 jours pour savoir quand rajouter 1j à l’année pour suivre au mieux les lunaisons.
|
|
Quel rythme ? C’est le même.
4 - Les années solaires
![]() Très difficile à mesurer
Très difficile à mesurer
![]() Choix du début : Solstice ou Équinoxe.
Choix du début : Solstice ou Équinoxe.
![]() Ça ne tombe toujours pas juste : 365,242199 = 365 j 5 h 48 mn 46 s
Ça ne tombe toujours pas juste : 365,242199 = 365 j 5 h 48 mn 46 s
![]() Sauf à changer d’année au milieu d’un jour, on s’arrange pour avoir un nombre entier de jours chaque année solaire donc voisin de 365 ou alternant une fois sur quatre 366 jours ou….
Sauf à changer d’année au milieu d’un jour, on s’arrange pour avoir un nombre entier de jours chaque année solaire donc voisin de 365 ou alternant une fois sur quatre 366 jours ou….
![]() Une bonne approximation est ¼, une année bissextile sur 4. C’est le calendrier julien.
Une bonne approximation est ¼, une année bissextile sur 4. C’est le calendrier julien.
![]() Une meilleure approximation est 6/25 = 24/100 car le siècle est intéressant donc on supprime l’année bissextile lors d’une année séculaire. (Mais le calendrier grégorien c’est seulement 3 années séculaires sur 4.)
Une meilleure approximation est 6/25 = 24/100 car le siècle est intéressant donc on supprime l’année bissextile lors d’une année séculaire. (Mais le calendrier grégorien c’est seulement 3 années séculaires sur 4.)
![]() Un peu plus précis est 8/33 = 24/99. Sur 4 siècles 96/396 et encore 4 ans (dont un bissextile) donne 97/400 ce qui correspond exactement au calendrier grégorien, mais ce n’est pas une meilleure approximation.
Un peu plus précis est 8/33 = 24/99. Sur 4 siècles 96/396 et encore 4 ans (dont un bissextile) donne 97/400 ce qui correspond exactement au calendrier grégorien, mais ce n’est pas une meilleure approximation.
![]() Quand a lieu le début de l’année ? Choix arbitraire ou lié aux saisons (solstices ou équinoxes) voire variable (Pâques, avènement d’un roi…) !!!
Quand a lieu le début de l’année ? Choix arbitraire ou lié aux saisons (solstices ou équinoxes) voire variable (Pâques, avènement d’un roi…) !!!
Exemple tiré de Généalogie des rois de France par Bouchet et édité en 1506 :
Charles VII alla à Trépas au chasteau d’Amboise le 7 avril 1497 avant Pasques, à compter l’année à la fête de Pasques ainsi qu’on le fait à Paris, et en 1498 à commencer à l’Annonciation de Nostre-Dame ainsi qu’on le fait en Aquitaine.
L’Annonciation est le 25 Mars (9 mois avant Noël bien évidemment).
5 - Fractions continues
![]() Reprenons ce que nous avons vu pour l’approximation de √15 / 5 = √(3/5).
Reprenons ce que nous avons vu pour l’approximation de √15 / 5 = √(3/5).
![]() Si maintenant on se donne un nombre à l’avance, il est facile de le transformer en fraction continue. On suit l’algorithme.
Si maintenant on se donne un nombre à l’avance, il est facile de le transformer en fraction continue. On suit l’algorithme.
- x0 = x
- On retranche sa partie entière y0, reste z0 = x0–y0
- On prend l’inverse de z0 soit x1
- Et on recommence avec x0 à la place de x0 (ou de x).
Quelques propriétés
- Si a/b est une réduite (une fraction obtenue par troncature) d’une fraction continue représentant un nombre x alors |a/b–x|≤1/b2.
- Si le développement est périodique, alors x est solution d’une équation du second degré.
- Si a/b est une réduite de x, alors de toutes les fractions de dénominateur inférieur à b, a/b est la meilleure approximation de x.
- Les réduites x sont alternativement plus petite et plus grande que x.
6 - Conclusion
![]() Il y a encore beaucoup à dire sur les liens entre mathématiques et calendrier. Citons tout simplement la découverte de formules permettant de passer d’un calendrier à un autre, de trouver automatiquement le nom du jour correspondant à telle date, de calculer la date de Pâques,...
Il y a encore beaucoup à dire sur les liens entre mathématiques et calendrier. Citons tout simplement la découverte de formules permettant de passer d’un calendrier à un autre, de trouver automatiquement le nom du jour correspondant à telle date, de calculer la date de Pâques,...
![]() Il y a là ce qu’on appelle des mathématiques discrètes (elles ne font appel qu’à des nombres entiers) et sont de ce fait liées à l’informatique. Ainsi la représentation d’une droite sur un écran (une suite de pixels) a beaucoup à voir avec la suite des longueurs des mois ou des années dans un calendrier ! Je n’en dirai pas plus.
Il y a là ce qu’on appelle des mathématiques discrètes (elles ne font appel qu’à des nombres entiers) et sont de ce fait liées à l’informatique. Ainsi la représentation d’une droite sur un écran (une suite de pixels) a beaucoup à voir avec la suite des longueurs des mois ou des années dans un calendrier ! Je n’en dirai pas plus.
Un article complémentaire de Anne Broise dans Images des Mathématiques.




Commentaires