On étudie un faisceau de cercle particulier associé à une homographie puis on présente les faisceaux de cercles produits par intersection d’une famille de plans avec une sphère et leur projection stéréographique.
Soit $f(z)=\frac{z-i}{z+i}$. On s’intéresse aux courbes de niveau du module de $f(z)$ et de son argument. Une première approche est d’observer la covariation de $z$ et $f(z)$, en renommant $z$ un point libre du plan et en définissant
w=(z-i)/(z+i)et pourquoi pas ses itérés
v=(w-i)/(w+i)
u=(v-i)/(v+i)On s’aperçoit alors que la fonction est d’ordre trois, sa réciproque est donc son carré, $f^{-1}(z)=f^2(z)=-i\frac{z+1}{z-1}$.
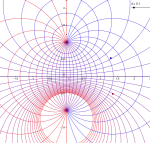
Pour visualiser le lieu des $z$ tels que $|f(z)|=k$, il suffit de prendre le lieu de sa réciproque $-i\frac{z+1}{z-1}$ lorsque $z$ décrit un cercle.
Pour avoir tout un faisceau de cercles, utilisons le tableur : en initialisant la première colonne A à un incrément décrivant $k$, on définit
B1=Point[Cercle[(0,0),A1]]un point sur le cercle de centre O et de rayon $k$ puis
C1=-i*(B1+1)/(B1-1)son image par $f^{-1}$ et enfin
D1=Lieu[C1,B1]le lieu recherché. On étend ces formules à toutes les trois colonnes.
On peut colorier le lieu d’une couleur qui dépend de $k$.
Pour l’argument constant, la seule variante est, si $k$ varie de 1 à 30 :
E1=Point[DemiDroite[(0,0),exp(2*i*A1*pi/30)]]
F1=-i*(E1+1)/(E1-1)
G1=Lieu[F1,E1]La figure est disponible sur i2geo
Projection stéréographique et faisceaux de cercles
On peut voir un faisceau de cercles comme la projection stéréographique d’un faisceau de cercles sur la sphère, lequel est produit par l’intersection d’une famille de plan partageant une même droite.
Nous allons illustrer ce point avec geospace. Construisons la sphère unité S. Son pôle Nord N et le plan $z=-1$ définissent la projection stéréogrpahique : un point M sur la sphère se projette sur le plan comme intersection de la droite (NM) et du plan.
Définissons une droite (AB) par deux points libres de l’espace. Cette droite peut intersecter la sphère ou pas. La famille de plans passant par (AB) intersecte la sphère. Si (AB) intersecte la sphère, tous les plans l’intersectent aussi en un faisceau de cercles à points base $I_1$ et $I_2$ (les points d’intersection), tandis que si (AB) n’intersecte pas la sphère, seule une portion de ces plans intersectera la sphère et formera un faisceau de cercles à points à points limite $J_1$ et $J_2$ (les points où les plans sont tangents à la sphère).
La droite (AB) est associée à une autre droite qu’on peut définir géométriquement comme l’intersection des deux plans tangents à S en $J_1$ et $J_2$ si (AB) intersecte la sphère, ou bien la droite $(J_1J_2)$ dans le cas contraire. Les deux faisceaux associés à ces deux droites sont conjugés, ils sont orthognaux et les points base de l’un sont les points limites de l’autre.
La projection stéréographique de ces faisceaux produit des familles de faisceaux de cercles du plan.

Commentaires