Vous trouverez toutes les constructions décrites ici sur i2geo.net où vous êtes invités à laisser des évaluations et des commentaires.
Résoudre une équation différentielle, c’est trouver une fonction $y$ dérivable, dont les dérivées vérifient une certaine équation.
Nous nous limiterons dans un premier temps à une fonction à valeur réelle vérifiant une équation différentielle du premier ordre $y'=f(x,y)$.
Cette équation nous donne la tangente de la fonction en chaque point du plan $(x,y)$, qu’on représente par le vecteur $(1,f(x,y))$ en ce point.
Considérons par exemple l’équation différentielle $y'=\sin(x^2\times y)$.
Commençons par un outil déjà intégré dans xcas. plotfield trace un champ de vecteurs, Tapez successivement chaque instruction dans la ligne de commande.
odesolve(sin(x^2*y),[x,y],[0,1],2)
plotfield(sin(x^2*y),[x,y])
plotode(sin(x^2*y),[x=-3..3,y],[0,1])
interactive_plotode(sin(x^2*y),[x,y])
 C’est idéal pour une visualisation rapide d’une solution particulière ou une allure du champs de vecteurs. On voit en particulier que la solution $y(-\infty)=0$ est instable, de très légères modifications des valeurs initiales entraînent de gros changements. Mais on ne sait pas exactement ce qu’Xcas fait. Nous allons maintenant dupliquer cette fonctionnalité avec d’autres logiciels.
C’est idéal pour une visualisation rapide d’une solution particulière ou une allure du champs de vecteurs. On voit en particulier que la solution $y(-\infty)=0$ est instable, de très légères modifications des valeurs initiales entraînent de gros changements. Mais on ne sait pas exactement ce qu’Xcas fait. Nous allons maintenant dupliquer cette fonctionnalité avec d’autres logiciels.
Champ de vecteurs
Commençons par tracer un champs de vecteurs. Nous pouvons représenter un champ de vecteurs par une grille de vecteurs régulièrement répartis entre deux points donnant la diagonale de la grille.
Les possibilités des différents logiciels apparaissent immédiatement : une grille s’implémentera à l’aide de deux boucles pour imbriquées en algorithmique, avec xcas ou carmétal, à l’aide du tableur avec géogébra, à l’aide de répétition ou de suites pour géoplan.
Avec Géogébra, on utilise le tableur qu’on fait apparaître avec Affichage>Tableur. Géogébra n’a pas la notion de fonction de deux variables. Il faudra donc modifier toutes les cases du tableur si on veut modifier la fonction.
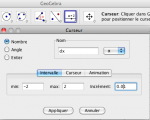 Créez deux points A et B dans la fenêtre ainsi qu’un curseur $dx$.
Dans la case A1, tapez "= A" . Le point A1 suit donc le point A.
Créez deux points A et B dans la fenêtre ainsi qu’un curseur $dx$.
Dans la case A1, tapez "= A" . Le point A1 suit donc le point A.
![]() En B1, tapez "=Vecteur[A1, A1 + dx*(1, sin(x(A1)^2*y(A1)))]". Vous obtenez le vecteur tangent au point A1 que vous pouvez déplacer. Pour rentrer cette formule, procédez par étapes : entrez d’abord une formule simple comme "=Vecteur[A1, A1 +(1,1)]", puis double cliquez dessus pour ouvrir une fenêtre d’édition plus lisible où vous pouvez taper l’expression plus compliquée.
En B1, tapez "=Vecteur[A1, A1 + dx*(1, sin(x(A1)^2*y(A1)))]". Vous obtenez le vecteur tangent au point A1 que vous pouvez déplacer. Pour rentrer cette formule, procédez par étapes : entrez d’abord une formule simple comme "=Vecteur[A1, A1 +(1,1)]", puis double cliquez dessus pour ouvrir une fenêtre d’édition plus lisible où vous pouvez taper l’expression plus compliquée.
En A2, tapez "=A1 + (x(B - A) / 10, 0)" puis tirez le petit coin carré vers le bas pour copier cette formule dans les 10 cases suivantes. Faites de même sur la colonne B. Vous avez ainsi, dans la case A10 par exemple, "A9+(x(B-A)/10,0)" et en B10, "Vecteur[A10, A10 + dx (1, sin(x(A10)² y(A10)))]". Ouvrez la fenêtre des propriétés pour cacher les points et ne montrer que les vecteurs.

En C1 taper "=A1+(0, y(B - A) / 10)", copiez B1 dans D1, A2 dand C2 et B2 dans D2, puis tirez les vers le bas. Sélectionnez la zonne C1:D10 et collez la dans E1-F10. Recommencez sur les 14 colonnes suivantes pour compléter le champ de vecteurs : sélectionnez G1:V10 et collez. De même qu’auparavant, cachez les points et montrez les vecteurs.
Une autre méthode, plus proche de celle de la double boucle fait appel à la notion de Séquence, tapez dans la barre de Saisie la formule suivante :
Séquence[Séquence[
Vecteur[(((10-i)*x(A)+i*x(B))/10,((10-j)*y(A)+j*y(B))/10),(((10-i)*x(A)+i*x(B))/10,((10-j)*y(A)+j*y(B))/10)+
dx*(1,sin((((10-i)*x(A)+i*x(B))/10)^2*((10-j)*y(A)+j*y(B))/10))]
,j,0,10],i,0,10]Encore une fois, préparez cette Séquence avec soin, par exemple dans un éditeur de texte, et par étapes. Avec un petit peu d’entrainement, on arrive à écrire de telles choses. Les choses seraient plus simples si on pouvait créer des fonctions un peu plus puissantes que simplement numériques.
Continuons avec carmétal qui se programme en javascript et une syntaxe particulière.
Nous allons créer une fonction $f(x,y)$ qui stockera le membre de droite de notre équation différentielle, qu’on pourra modifier à loisir ensuite.
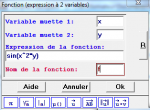
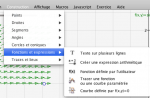 Cherchez donc dans le menu Construction>Fonctions et expressions>Fonction définie par l’utilisateur, dans l’onglet "Numérique" qui apparaît dans l’inspecteur d’objets, donnez lui le nom $f$, faites la dépendre des variables x et y (à droite) et entrez l’expression $sin(x^2*y)$.
Cherchez donc dans le menu Construction>Fonctions et expressions>Fonction définie par l’utilisateur, dans l’onglet "Numérique" qui apparaît dans l’inspecteur d’objets, donnez lui le nom $f$, faites la dépendre des variables x et y (à droite) et entrez l’expression $sin(x^2*y)$.
 Définissez également un pas d’intégration dx sous forme d’un curseur que vous trouverez dans la barre d’outils Contrôles. Nommez le "dx", d’incrément 0,01, entre -2 et 2.
Définissez également un pas d’intégration dx sous forme d’un curseur que vous trouverez dans la barre d’outils Contrôles. Nommez le "dx", d’incrément 0,01, entre -2 et 2.
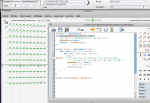
 Ouvrez l’éditeur : "Javascript>Ouvrir l’éditeur de script" et tapez le code suivant :
Ouvrez l’éditeur : "Javascript>Ouvrir l’éditeur de script" et tapez le code suivant :
vecteur = function(a) {
var p=Point("x("+a+") + dx",
"y("+a+") + dx*f(x("+a+"), y("+a+"))");
SetHide(p,true);
return Vector(a,p);
}
quadrillage = function(r1,r2) {
for (var i=0; i<11; i=i+1){
for (var j=0; j<11; j=j+1){
qij = Point("("+i+"*x("+r1+")+"+(10-i)+"*x("+r2+"))/10",
"("+j+"*y("+r1+")+"+(10-j)+"*y("+r2+"))/10");
SetHide(qij, true);
// Juste le vecteur
vecteur(qij);
}
}
}
quadrillage(Point(),Point());Nous y définissons deux fonctions, la fonction vecteur qui prend un point $a$ et trace le vecteur entre les points $a$ et $p=(x(a)+dx,y(a)+dx\times f\bigl(x(a),y(a)\bigr)$, la fonction quadrillage qui trace 11x11 vecteurs entre deux points donnés, et enfin un appel de cette fonction quadrillage avec deux nouveaux points pris au hasard dans la fenêtre.
La manière un peu cryptique de noter le point $p$ est due au fait que nous voulons que carmétal ne place pas le point $p$ aux coordonnées actuelles mais fixes du point $a$ mais plutôt qu’il stocke une expression fonctionnelle en les coordonnées de $a$. On stocke donc une chaîne de caractère où $a$ intervient par son nom (qui n’est pas en général la lettre "a"). On concatène deux chaînes de caractères avec le symbole +.
Le quadrillage fait appel à deux boucles pour imbriquées, allant de 0 à 10 (compris, soit 11x11 points). On place un vecteur au point de coordonnées $\left(\frac{i\times x(r_1)+(10-i)\, x(r_2)}{10}, \frac{j\times y(r_1)+(10-j)\, y(r_2)}{10}\right)$.
On stocke ce script dans la figure en cliquant sur la coche ".zir", apparaît alors un bouton de script qui permet de gérer les scripts de la figure. On peut aussi lancer le script en cliquant sur le "feu vert". On déplace le champ de vecteurs au travers des deux points qui le définissent.
Avec Géoplan, on peut utiliser une fonctionnalité similaire au copier-coller du tableur : la répétition de création d’objets, ou similaire aux séquence avec des suites.
Créez une fonction f à deux variables $f(x,y)=\sin(x^2\times y)$, deux points libres M0 et M99 qui seront les extrémités diagonales de notre champs de vecteur. Vous pouvez les afficher en gras pour qu’on les repère mieux.
On rencontre tout de suite l’esprit didactiquement très ferme (certains disent rigide) de géoplan : les vecteurs ne sont pas visibles sous géoplan, car ce ne sont pas des ensembles de points. Nous allons représenter un vecteur ancré en un point par un segment (on peut raffiner, voir le fichier joint).
Créez un point libre C, les deux grandeurs xC et yC associées à ses coordonnées, une grandeur dx réelle entre 0 et 1 de pas 0.01 (Piloter>Affecter...libre à 0,5), puis un point D par ses coordonnées (xC+dx,yC+dx*F(xC,yC)) dans le repère Roxy et finalement le segment [CD] que vous nommez s. Vous pouvez bouger C et observer le champs de vecteurs.
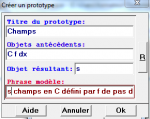 Pour ne pas à refaire toute cette construction du champs en un point, définissons un prototype (Menu Divers>Créer un prototype), que vous nommez Champs, dont les objets antécédents sont C F dx (séparés par un espace), l’objet créé est le segment s (on ne peut pas mettre le segment anonyme CD comme objet résultant, il faut le nommer) et la phrase de construction est "s champs en C défini par f de pas dx". Vous avez maintenant dans votre figure le prototype suivant (Editer>Editer le texte de la figure) :
Pour ne pas à refaire toute cette construction du champs en un point, définissons un prototype (Menu Divers>Créer un prototype), que vous nommez Champs, dont les objets antécédents sont C F dx (séparés par un espace), l’objet créé est le segment s (on ne peut pas mettre le segment anonyme CD comme objet résultant, il faut le nommer) et la phrase de construction est "s champs en C défini par f de pas dx". Vous avez maintenant dans votre figure le prototype suivant (Editer>Editer le texte de la figure) :
Début de [Champs]
C point donné
F fonction à 2 variables donnée
dx réel donné
xC abscisse de C (repère Roxy)
yC ordonnée de C (repère Roxy)
D point de coordonnées (xC+dx,yC+dx*F(xC,yC)) dans le repère Roxy
s Segment CD
Description de l'interface
s champs en C défini par F de pas dx
Antécédent 1 (point):
Antécédent 2 (fonction à 2 variables):
Antécédent 3 (nombre réel):
Résultat (polygone):
Le vecteur en C défini par la dérivée f et la longueur dx.
Fin de [Champs]Vous pouvez maintenant appliquer ce prototype à M0 et M99 (donner la fonction f et dx à chaque fois) avec Créer>Objet selon prototype.
Nous allons maintenant créer une répétition de ces "vecteurs" pour former une grille.
Créez donc deux grandeurs numériques issues d’un calcul géométrique, dxM et dyM resp. l’abscisse et l’ordonnée du vecteur $\vec{M0M99}/9$ qui se note vec(M0,M99)/9 ; puis les vecteurs vec(k) et vec(l) par leurs coordonnées (dxM,0), resp. (0,dyM) (dans le repère Roxy).
Définissez les points M01 et M10 images de M0 par les translations de vecteurs respectivement vec(k) et vec(l) (Créer>Point>Point image>Translation par vecteur). Placez y deux "vecteurs" par prototype que vous appelez s01 et s10 respectivement.
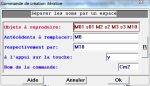 Nous allons maintenant répéter chacune de ces constructions 8 fois en créant des commandes : Créer>Commande>Création itérative, pour la rangée horizontale les objets à reproduire sont M01 et s01, l’antécédent est M0 à remplacer par M01, à l’appui de la touche x (par exemple). Une fois créée, appliquez 8 fois cette commande pour créer la rangée horizontale.
Nous allons maintenant répéter chacune de ces constructions 8 fois en créant des commandes : Créer>Commande>Création itérative, pour la rangée horizontale les objets à reproduire sont M01 et s01, l’antécédent est M0 à remplacer par M01, à l’appui de la touche x (par exemple). Une fois créée, appliquez 8 fois cette commande pour créer la rangée horizontale.
Faites de même pour la rangée verticale, où cette fois les objets à reproduire sont tous les objets de la rangée horizontale, soit M01, s01, M2, s2, M3, s3... et M10, s10 (séparés par un espace). La limite de la fenêtre fait que vous ne pouvez pas rentrer les 9 points, il vous faut en rentrer quelques uns puis éditer le texte de la figure et trouver la ligne à éditer à la main :
Cm2 (touche Y) itération: M01, s01, M2, s2, M3, s3, M4, s4, M5, s5, M6, s6, M7, s7, M8, s8, M9, s9, M10, s10 en remplaçant M0 respectivement par M10que vous appliquez 9 fois (un vecteur extra est créé, vous pouvez l’effacer).
Vous ne pouvez créer cette commande qu’une fois que les points horizontaux sont créés.
Méthode d’Euler
Pour intégrer numériquement une équation différentielle, différentes méthodes sont à notre disposition. Nous allons commencer par la plus simple, la méthode d’Euler. Nous discrétisons la coordonnée $x$ en une suite $x_n=x_0+n\delta_x$ où $\delta_x$ est un petit nombre et calculons une suite $y_n$ de valeurs qui lui corresponde et soit une solution approchée.
On définit avec la méthode d’Euler tout simplement $y_{n+1}=y_n+ \delta_x\, f(x_n, y_n)$ avec une valeur de départ $(x_0, y_0)$.
Passons donc à Géogébra pour programmer cette intégration numérique à l’aide du tableur :
Définissez un point, disons E, et tapez dans une case libre (par exemple A14), "=E" de manière à actualiser cette cellule quand vous bougez le point. En A15, tapez la formule "=A14 + dx*(1, sin(x(A14)^2*y(A14)))" (procédez par étapes "=A14+dx" puis double-cliquez pour éditer dans une fenêtre plus grande). Une fois que la formule est validée, étendez la sur une vingtaine de lignes vers le bas. Cachez les points (clic-droit>propriétés). En B15 tapez la formule "Segment[A14, A15]" et étendez la vers le bas. Changez la couleur des segments pour bien les voir, sans leur étiquette. Vous pouvez copier la zone A14:B35 dans la cellule C14 pour l’attacher à un autre point (C14=F par exemple).
Jouez avec dx pour voir son effet sur la courbe intégrale. Vous pouvez tracer la trace de la colonne de segments pour visualiser les courbes intégrales.
 Avec Géoplan, nous définissons une suite numérique récurrente d’ordre 1 définie à partir de 0, dont la valeur du premier terme est yC et dont le terme de rang n est défini par Y(n-1)+dx*f(xC+dx*n,Y(n-1)). Pour visualiser, nous définissons un entier libre n entre 0 et 1000, et un point M de coordonnées (xC+dx*n, Y(x)), puis la ligne L lieu du point M piloté par n.
Avec Géoplan, nous définissons une suite numérique récurrente d’ordre 1 définie à partir de 0, dont la valeur du premier terme est yC et dont le terme de rang n est défini par Y(n-1)+dx*f(xC+dx*n,Y(n-1)). Pour visualiser, nous définissons un entier libre n entre 0 et 1000, et un point M de coordonnées (xC+dx*n, Y(x)), puis la ligne L lieu du point M piloté par n.
 Vous pouvez tracer la trace L pour visualiser les courbes intégrales quand vous pilotez C (vous pouvez également affecter ses coordonnées de manière aléatoire et répétitive).
Vous pouvez tracer la trace L pour visualiser les courbes intégrales quand vous pilotez C (vous pouvez également affecter ses coordonnées de manière aléatoire et répétitive).
Avec carmétal, on définit une fonction, qui prend un point et un nombre de pas et qui va appliquer n fois $p=\bigl(x_q+dt,y_q+dt\times f(x_q, y_q)\bigr)$, en commençant avec le point paramètre, et en écrasant ensuite la valeur du point $q$ par celle nouvellement calculée $p$. Pour le rendu visuel, on rend les points invisibles tout en traçant les segments. On applique enfin l’algorithme à un point.
euler = function(a,n) {
var q = Point("","x("+a+")","y("+a+")");
SetHide(q,true);
for (var i=1; i<n; i=i+1){
var p=Point("","x("+q+") + dt",
"y("+q+") + dt*f(x("+q+"), y("+q+"))");
SetHide(p,true);
Segment(q,p);
q = p;
}
return q;
}
euler(Point(),150);Méthode de Runge-Kutta d’ordre 2
Cette méthode est d’ordre 2 car pour chaque nouveau point, on a besoin d’évaluer la fonction $f$ deux fois, ce qui est supposé être coûteux d’un point de vue temps de calcul.
$y_{n+1} = y_n + \delta_x\bigl((1-\frac1{2\alpha})f \left(x_n, y_n \right) + \frac1{2\alpha}f \left(x_n + \alpha\,\delta_x, y_n + \alpha\,\delta_x\, f \left(x_n, y_n \right) \right)\bigr)$
On en prend un cas particulier appelée "Euler du point milieu", qui est une méthode d’Euler composée, définissant $y_{n+1}=y_n+\delta_x\,f(x'_n,y'_n)$ où $(x'_n,y'_n)$ est un point issu de $(x_n, y_n)$ par une étape d’Euler pour le pas $\delta_x/2$.
Avec Géoplan, nous définissons une suite numérique récurrente d’ordre 1 définie à partir de 0, dont la valeur du premier terme est yC et dont le terme de rang n est défini par Z(n-1)+dx*f(X(n-1)+dx/2,Z(n-1)+(dx/2)*f(X(n-1),Z(n-1))) en définissant pour plus de clarté la suite non récurrente X(n)=xC+n*dx.
Avec Géogébra, on procède comme précédemment mais avec une colonne supplémentaire pour le résultat intermédiaire du point milieu :
Copiez-collez X la zone A14:B35 en D14. Tapez (0,0) en F13 puis copiez D15 en F14. Modifiez la formule en F14 pour D14 + d/2 (1, sin(x(D14)² y(D14))). Etendez la vers le bas à toute la colonne. Vous voyez ainsi apparaître les points milieu, au milieu des segments. Puis modifiez la formule en D15 pour D14 + d (1, sin(x(F14)² y(F14))) qui prend donc maintenant la valeur de la dérivée au point milieu, qui est dans la colonne F.
Avec CaRMétal, on créée un nouveau script
rk2 = function(a,n,alpha) {
var q = Point("","x("+a+")","y("+a+")");
SetHide(q,true);
for (var i=1; i<n; i=i+1){
var r=Point("","x("+q+")+"
+alpha
+"*dt",
"y("+q+")+"+alpha+"*dt*f(x("+q+"), y("+q+"))");
var p=Point("","x("+q+") + dt",
"y("+q+") + dt/"+(2*alpha)+"*("+
(2*alpha-1)+
"*f(x("+q+"), y("+q+"))+f(x("+r+"), y("+r+")))");
SetHide(p,true);
SetHide(r,true);
SetRGBColor(Segment(q,p),0,0,255);
q = p;
}
return q;
}
//rk2("A",15,1); // alpha = 1: Euler-Cauchy /Heun
rk2("A",15,0.5); // alpha = 0.5: Euler-point milieuDeuxième ordre
Les équations intéressantes, qui proviennent de la physique, sont le plus souvent du deuxième ordre, elles sont le résultat de l’application de la loi de Newton qui dit que le mouvement d’un point est le résultat des forces qui lui sont appliquées et qui influent sur son accélération, c’est-à-dire que la dérivée seconde de la trajectoire est connue quand on connait les forces. La variable principale est le temps $t$, et on dénote la dérivation par rapport au temps avec un point plutôt qu’avec un prime.
$\vec{F}=m\,\vec{a}.$
Pour calculer le mouvement d’un mobile, il faut donc intégrer une équation du second ordre. Considérons le pendule simple, une masse est pendue à un fil rigide. Quelle est sa trajectoire ? Les deux forces qu’il subit sont la gravitation (constante vers le bas de module mg) et la réaction du fil, qui s’ajuste de manière à annuler la composante radiale de la pesanteur. La résultante est donc la composante tangentielle de la pesanteur, soit, si $\theta$ est l’angle avec la verticale, qu’on prendra comme coordonnée principale et $\ell$ la longueur du fil, $m\,\ell\,\ddot\theta = - m\, g\sin(\theta)$.
On peut avec la géométrie interactive, intégrer l’équation et également visualiser le mouvement du pendule.
On doit donc intégrer la position $\theta$ et la vitesse $\dot\theta$ traitées comme deux fonctions différentes.
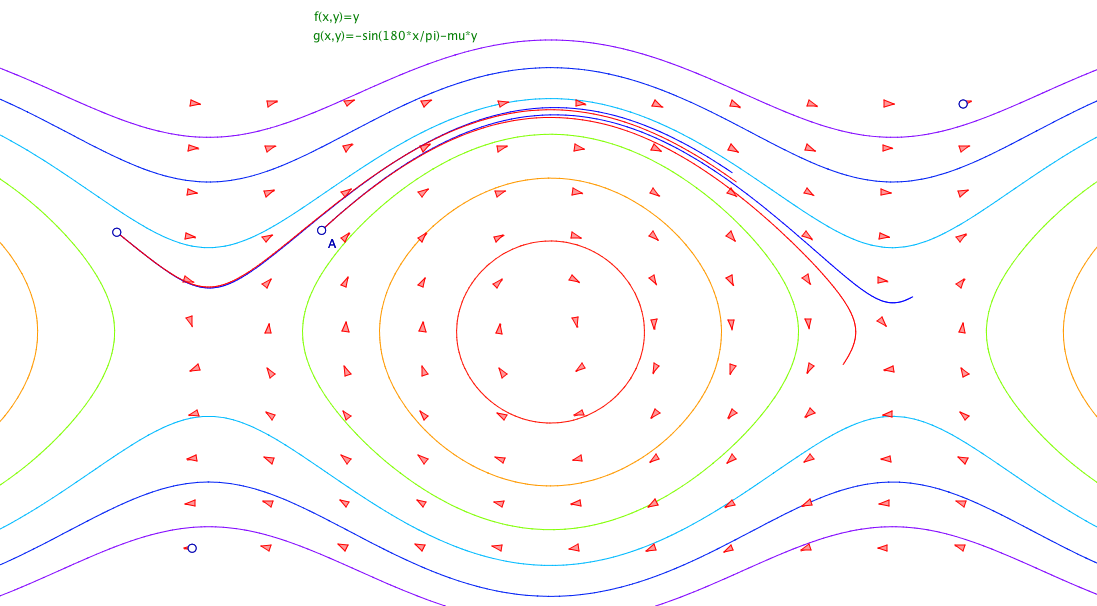
Les équations du premier ordre en dimension deux $\dot x = f(x,y)$, $\dot y =g(x,y)$ généralisent les équations du second ordre $\ddot \theta = g(\theta, \dot\theta)$ en prenant $x=\theta$ la position et $y=\dot\theta$ la vitesse. Quand on visualise une variable abstraite (la vitesse) comme une dimension du système, on dresse le portrait de phase du système dynamique.
On prendra donc la variable de position $\theta$ du pendule horizontalement selon l’axe des $x$ et la vitesse angulaire $\dot\theta$ verticalement selon l’axe des $y$. Les équations deviennent donc $\dot x = y$ et $\dot y = \ddot x = g(x,y)$.
Généralisons les algorithmes que nous avons défini précédemment pour les équations d’ordre un à deux dimensions.
Avec CaRMetal, on crée une variable dt et deux fonctions à deux variables $f(x,y)=y$ et $g(x,y)=-sin(180*x/pi)-mu*y$ (en négligeant les valeurs de la pesanteur et de la longueur du fil). Le quadrillage doit être légèrement adapté :
// Deux fonctions f(x,y) et g(x,y)
// définissent un champs de vecteurs qu'on trace par un
// vecteur en q de taille dt (définie par l'utilisateur)
vecteur = function(q) {
var p = Point("x("+q+") + dt*f(x("+q+"), y("+q+"))",
"y("+q+") + dt*g(x("+q+"), y("+q+"))");
SetHide(p,true);
// Rouge par défaut
SetRGBColor(Segment(q,p),255,0,0);
}
champs = function(q,p,n) {
for (var i = 0; i<=n; i=i+1){
for (var j=0; j<=n; j=j+1){
var r = Point("x("+p+")+"+(i /n)+"*(x("+q+")-x("+p+"))","y("+p+")+"+(j /n)+"*(y("+q+")-y("+p+"))");
SetHide(r,true);
vecteur(r);
}
}
return q;
}
champs(Point(),Point(),20);Et l’intégration également :
// Deux fonctions f(x,y) et g(x,y) définies par l'utilisateur
// ainsi qu'un curseur dt petit
// On trace l'orbite partant du point q en n étapes
euler = function(q,n) {
for (var i = 1; i<n; i=i+1){
var p = Point("x("+q+") + dt*f(x("+q+"), y("+q+"))",
"y("+q+") + dt*g(x("+q+"), y("+q+"))");
SetHide(p,true);
SetRGBColor(Segment(q,p),0,0,255);
q = p;
}
return q;
}
rk = function(q,alpha,n) {
for (var i = 1; i<n; i=i+1){
var r=Point("x("+q+")+"
+alpha
+"*dt*f(x("+q+"), y("+q+"))",
"y("+q+")+"+alpha+"*dt*g(x("+q+"), y("+q+"))");
SetHide(r,true);
var p=Point("","x("+q+") + dt/"+(2*alpha)+"*("+
(2*alpha-1)+
"*f(x("+q+"), y("+q+"))+f(x("+r+"), y("+r+")))",
"y("+q+") + dt/"+(2*alpha)+"*("+
(2*alpha-1)+
"*g(x("+q+"), y("+q+"))+g(x("+r+"), y("+r+")))");
SetHide(p,true);
SetRGBColor(Segment(q,p),255,0,0);
q = p;
}
return q;
}
a = Point();
euler(a,150,0,0,255); // Euler Bleu
rk(a,1,150,255,0,0); // Runge-Kutta alpha = 1 (méthode de Heun) RougeLes équations intéressantes de la physique sont issues de la mécanique hamiltonienne où une fonctionnelle énergie $H(x,y)$ est conservée au cours du temps dans le cas non dissipatif sans friction et diminue dans le cas dissipatif. Ici, l’énergie est la somme de l’énergie potentielle de pesanteur et de l’énergie cinétique $H(x,y)=m\,g\,\ell\,(1-\cos(x))+\frac12m(\ell y)^2$.
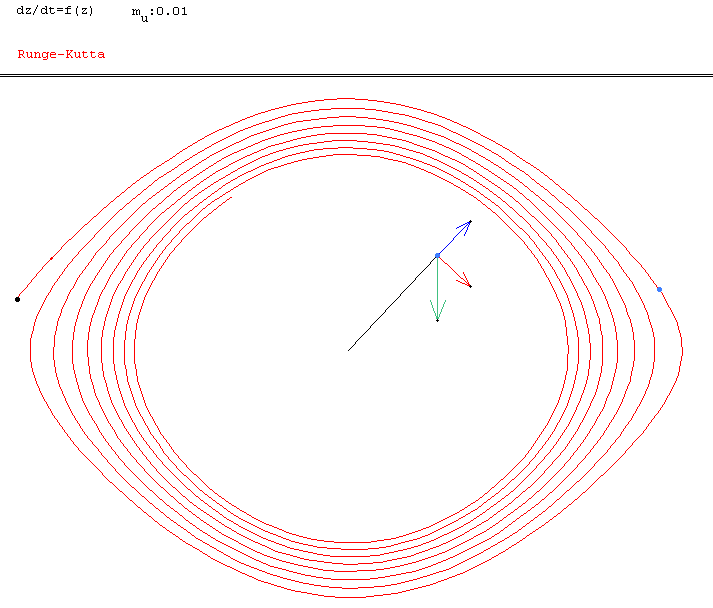
Mises dans le cadre de la mécanique hamiltonienne, en terme des variables conjuguées de position $q=\ell\,x$ et de quantité de mouvement $p=m\ell\,y$, les équations d’évolution sont alors $\dot q=\frac{\partial H}{\partial p}$, $\dot p=-\frac{\partial H}{\partial q}$ ainsi le vecteur tangent $(\dot q, \dot p)$ est perpendiculaire au gradient de l’énergie $(\frac{\partial H}{\partial q}, \frac{\partial H}{\partial p})$ qui pointe vers la plus grande pente.
On peut voir que la méthode de Runge-Kutta (d’ordre 2), préserve bien ces équipotentielles d’énergie, les orbites rouges restent à énergie constante (dans le cas sans friction) tandis que la méthode d’Euler "part dans le décor" en sous-estimant systématiquement la courbure des orbites. C’est un aspect très important des équations différentielles, qu’on décompose en partie conservative et partie dissipative pour une certaine fonctionnelle énergie, somme d’une énergie cinétique dépendant de la vitesse et d’une énergie potentielle dépendant de la position et parfois de la vitesse.
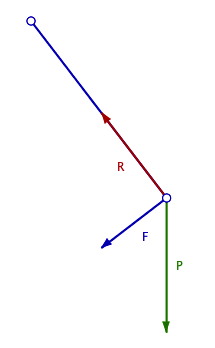
On peut également animer le pendule pesant lui-même, plus concrètement que dans un diagramme de phase : Construisons donc un point M sur un cercle de centre l’origine et de rayon 1, un vecteur vitesse de départ défini par un point P1 proche de M. On définit trois grandeurs numériques, dt, gsl (pour $g/\ell$) et mu qui contrôlent le pas, la pesanteur et la friction.
euler = function(n) {
var m = "M"; // Le point
var t = Math.atan(X(m)/Y(m)); // L'angle
for (var i = 1; i<n; i=i+1){
var tp = Math.asin((X("P1")-X(m))/Math.cos(t)); // la vitesse
var dt = GetExpressionValue("dt");
var gsl = GetExpressionValue("gsl");
var mu = GetExpressionValue("mu");
var t = t+dt*tp;
var tp = tp + dt*(-gsl*Math.sin(t)-mu*tp);
Move(m,Math.sin(t),-Math.cos(t));
Move("P1",X(m)+Math.sin(tp)*Math.cos(t),Y(m)+Math.sin(tp)*Math.sin(t));
Pause(100);
}
}
euler(150);Avec Géoplan, nous définissons une suite complexe récurrente d’ordre 1 définie à partir de 0, dont la valeur du premier terme est le complexe affixe du point de départ, et dont le terme de rang n est défini par Z(n-1)+dt*f(Z(n-1)+(dt/2)*f(Z(n-1))) en définissant les deux fonctions réelles en une seule fonction complexe, f fonction de C dans C : z|->im(z)-i*(sin(re(z))+mu*im(z)) avec x=re(z), y=im(z) cela s’écrit donc $\frac{\partial x}{\partial t}=y$ et $\frac{\partial y}{\partial t}=-sin(x)+mu*y$.
On peut également représenter le pendule animé avec l’option "Piloter>Temps actif" qui met à jour une variable "time". On a ainsi le point de départ dans l’espace de phase piloté à la souris, le point du mobile sur la courbe intégrale et la position correspondante d’un modèle du pendule, avec les forces de pesanteur, de réaction et la résultante totale.
Avec Geogebra, l’utilisation du tableur permet de faire à peu près les mêmes choses.




Commentaires