Retrouver les fichiers associés à cette activité sur i2geo.net. Nous allons nous intéresser aux suites, à leurs valeurs d’adhérence, au moyen de les représenter visuellement, aux suites en particulier de la forme $u_{n+1}=f(u_n)$, aux moyens d’accélérer la convergence quand $f$ a un point fixe attractif.

Tout d’abord, une valeur d’adhérence $v$ d’une suite $(u_n)_{n\in\mathbb{N}}$ est un nombre qui est approché arbitrairement près par toute queue de la suite, c’est-à-dire, $\forall\epsilon>0,\forall N\in\mathbb{N}, \exists n>N, |u_n-v|<\epsilon$.

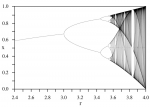
La suite qui va nous occuper est la suite logistique qui exhibe des propriétés intéressantes. Il s’agit de l’itération de la fonction $f_a:x\mapsto a\,x\,(1-x)$ pour une valeur de départ dans $[0,1]$ et $0

Théorème du point fixe de Picard

Une fonction $f:A\to A$ sur un fermé $A$ de $\mathbb{R}^d$, K-contractante admet un unique point fixe $\bar x\in A$ et la suite de ses itérées $x_n=f^n(x_0)$ converge vers $\bar x$ avec $||x_k-\bar x||\leq \frac{K^{k-\ell}}{1-K}||x_{\ell+1}-x_\ell||$ pour tous entiers $k\geq \ell\geq 0$.

Notre fonction $f_a$ a deux points fixes sur $\mathbb{R}$, $x=0$ et $x=1-\frac1a$, qui n’est positif que pour $a\geq 1$.

Le maximum de la dérivée $f'_a(x)=a\,(1-2\,x)$ de $f_a$ est atteint aux bornes et vaut $a$, $f_a$ est donc contractante pour $a<1$, avec $0$ comme unique point fixe attractif, lequel devient répulsif pour $a>1$. La dérivée en l’autre point fixe vaut $2-a$ qui est plus petit que $1$ en valeur absolue pour $1

A noter le cycle d’ordre 3 pour $a=1+\sqrt{8}$.

Une étude fine avec Géoplan par Olivier Roizès m’a servi de guide.