Un arc plan $\gamma: \mathbb{R}\longrightarrow \mathbb{R}^2$ dérivable deux fois définit un vecteur vitesse $\dot\gamma=\frac{d\,\gamma}{d\,t}$. L’abscisse curviligne est la longueur de la courbe depuis l’origine, $s=\int_0^t ||\dot\gamma(\tau)||d\,\tau$.
Quand la paramétrisation est par longueur d’arc, c’est-à-dire quand $||\dot\gamma||=1$, on paramétrise plutôt par $s$ et on note la dérivée $T=\gamma'=\frac{d\,\gamma}{d\,s}$ le vecteur tangent unitaire. En dérivant $||\gamma'||^2=<\gamma',\gamma'>=1$, on obtient $<\gamma'',\gamma'>+<\gamma',\gamma''>=2\,<\gamma',\gamma''>=0$. Donc $N=\frac{\gamma''}{||\gamma''||}$ est orthogonal à $T$.
La courbure est $c(s)=<\gamma'',N>$.
En paramétrisation à vitesse non constante, il faut faire un changement de variable avec $\frac{d\,s}{d\,t}=||\dot\gamma||$ et ne garder dans $\ddot\gamma=\frac{d^2\,\gamma}{d\,t^2}$ que le terme normal et non pas tangentiel, soit $\frac{d\,\gamma}{d\,s}=\frac{~\frac{d\,\gamma}{d\,t}~}{\frac{d\,s}{d\,t}}$ puis $\frac{d^2\,\gamma}{d\,s^2}=\frac{\frac{\dot\gamma}{||\dot\gamma||}}{d\,t}/{\frac{d\,s}{d\,t}}=(\ddot\gamma-\dot\gamma\frac{<\dot\gamma,\ddot\gamma>}{||\dot\gamma||^2})/{||\dot\gamma||^2}$, la première partie ayant une composante normale, la deuxième étant purement tangentielle. Donc
$c(t)=\frac{<\ddot\gamma, N>}{||\dot\gamma||^2}$.
Le cercle osculateur au point $\gamma(t)$ est de rayon $r(t)=1/c(t)$ et de centre $\gamma(t)+r(t) N$. À part aux maxima de courbure, la courbe traverse le cercle osculateur en lui étant tangent.
La développée est le lieu des centres de courbure et l’enveloppe des normales. Une développante est définie par une longueur $s_0$ et $\gamma(s)-\gamma'(s)\times(s-s_0)$. La développée d’une développante est la courbe elle-même.
Implémentation avec Géogébra
On définit une courbe paramétrée, par exemple en définissant une courbe polaire $r(t)\,(cos(t), sin(t))$. Géogébra ne reconnait que les fonctions de $x$ donc on tape dans la ligne de saisie (par exemple) r=1+0.1*cos(x)+0.05*cos(3*x) puis a=Courbe[r(t) cos(t), r(t) sin(t), t, 0, 2*pi] qui trace la courbe paramétrée. Puis les dérivées : Dérivée[a] qu’il nomme a’ et Dérivée[a’] qu’il nomme a’’. Fabriquez ensuite un curseur t entre 0 et 2π, le point correspondant sur la courbe A=a(t), un réel v=Longueur[a’(t)], le vecteur tangent T=Vecteur[a’(t)/v] qu’on positionne en A (clic-droit>Propriétés>Position choisir A), la droite tangente Droite[A, A + T], le vecteur normal N=i * T (il y a identité entre les vecteurs et les nombres complexes), positionné aussi en A, la droite normale Droite[A, A + N], la courbure c=a’’(t)*N/v^2 (le produit entre deux vecteurs est un produit scalaire), le rayon=1/c, le centre de courbure O=a(t)+rayon*N, et finalement le cercle osculateur de centre O et du rayon calculé. Faire le lieu de O quand t décrit [0,2π] génère la développée. C’est aussi l’enveloppe des normales, cliquer droit sur la droite normale et activer la trace pour le voir. Associer la droite normale et le centre du cercle à une case à cocher "développée". Les maximas de courbure lui provoquent des points de rebroussement, les points d’inflexion des asymptotes.
Pour calculer l’abscisse curviligne depuis l’origine, il faut intégrer numériquement la longueur de a’ entre 0 et t, $s=\int_0^t ||\dot\gamma(\tau)||d\,\tau$. Préparons un pas dt=t/98. Ouvrez le tableur, préparez une première colonne partant de 0 et augmentant de dt à chaque case et augmentant de dt à chaque case : A1="$\tau$", A2=0, A3=A2+dt que vous copiez sur la colonne jusqu’à A100. La deuxième colonne est le calcul de s, B1="s", B2=0, B3=B2+dt*Longueur[a’((A2+A3)/2)] par la méthode des rectangles au point milieu, qu’on généralise à toute la colonne. On fait afficher s=B100 quelque-part. On vérifie que pour r=1 (le cercle unité), on a bien identité entre s et t.
Une développante est définie par un curseur $s_0$ entre -5 et 5, par le lieu du A-T*(s - s_0) . Associer la tangente et ce point (activé pour la trace) à une case à cocher "développante".
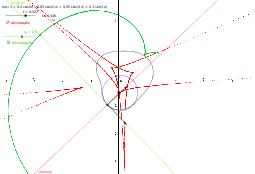
- Une courbe polaire, son cercle osculateur, sa développée, une développante
Courbe définie par courbure
Si on donne une fonction c(s), il existe, à un déplacement près, une unique courbe plane ayant cette fonction courbure. En notant $a'(s)=e^{i\,\theta(s)}$ le vecteur tangent unitaire relevé comme associé à un angle réel $\theta$, la courbure s’exprime comme $a''(s)=i\,\theta' e^{i\,\theta(s)}=c(s) N$, soit $c(s)=\theta'$. On peut donc intégrer numériquement la fonction $c$ pour obtenir la fonction direction $\theta$, qui permet ensuite, par intégration de $e^{i\,\theta(s)}$, de trouver la position $a$. Après la définition de la fonction c=log(x) (par exemple), d’un curseur ds entre 0 et 0.1, de pas 0.01, on ouvre donc le tableur, dans la première colonne, A1="s", A2=0, A3=A2+ds qu’on généralise à toute la colonne, la deuxième colonne B1="\theta", B2=0, B3=B2 + ds*c((A2 + A3) / 2) qu’on généralise, et la troisième colonne C1="A", C2=(0,0) (par exemple), C3=C2 + ds*exp(i*(B3 + B2) / 2), qu’on généralise. On cache ces points et on les visualise sous forme de segments D3=Segment[C2, C3] dont on cache les étiquettes. La longueur de chacun de ces segments est ds.
Pour prouver que notre courbe remplit bien les conditions visées, on visualise un point sur la courbe, le cercle osculateur discret et le cercle osculateur cible. Pour cela, on sélectionne la colonne des points, on clique-droit pour la transformer en liste "points", on construit un curseur entier n entre 0 et 100, l’abscisse curviligne s=n*ds, le point correspondant A=Elément[points, n] avec son repère mobile défini par $\theta$=Elément[angles, n], T=Vecteur[exp(i θ)], N=i*T à positionner en A. On trace le cercle osculateur discret défini par trois points successifs Cercle[Elément[points, n - 1], A, Elément[points, n + 1]], son centre, et le cercle osculateur cible défini par son rayon r=1/c(s), et son centre O= A+ r*N. On peut voir que les deux cercles sont très proches, à part quand la courbure est faible.
On peut tabuler ceci en comparant les courbures discrètes et visées :
E3=1 / Rayon[Cercle[C2, C3, C4]]
F3=c(A3)
G3=100*(1 - abs(E3 / F3))
- Une courbe définie par une fonction courbure
On voit des effets de l’intégration numérique en prenant un problème mal conditionné comme c(x)=1/(1-x), le point correspondant à s=1 étant de rayon de courbure nulle, l’intégration au point suivant dépend énormément du pas de discrétisation.
Transformée de Fourier
Comment fabriquer une courbe fermée un peu "rigolote", c’est-à-dire passant "par" des points donnés ? Disons n=12 (curseur entier jusqu’à 30) points répartis autour de 0, soit dθ=2*π/n. Dans le tableur : ligne de titre A1="k", B1="θk", C1="Ak", D1="rk", A2=0, A3=A2+1, B2=0,B3=B2+dθ, C2=Point[Droite[(0, 0), exp(i*B2)]], D2= C2*exp(i B2) (il s’agit ici du produit scalaire entre deux vecteurs du plan), les formules sont à généraliser sur la colonne jusqu’à 31 (disons). Les points sont à "décoller" à la main de (0,0). Remarquez le produit scalaire sur la colonne D plutôt que Longueur(CXX) qui serait toujours positif.
Puis nous créons les listes d’angles θk et de rayons rk correspondants. Convenons qu’ils définissent une fonction $f$ $2\pi$-périodique, constante par morceau valant $r_k$ sur $[\theta_k-d\theta/2,\theta_k+d\theta/2[$. Les coefficients de Fourier sont $a_k=\frac1{\pi}\int_0^{2\,\pi}cos(k\,\theta)\,f(\theta)\,d\theta$, k>0 et $b_k=\frac1{\pi}\int_0^{2\,\pi}sin(k\,\theta)\,f(\theta)\,d\theta$. Le terme constant $a_0=\frac1{2\,\pi}\int_0^{2\,\pi} f(\theta)\,d\theta$ pose quelques petites complications.
Comme $\int_a^{b}cos(k\,\theta)\,d\theta=\frac 1k[\sin(k\,b)-\sin(k\,a)]$, de même pour les $b_k$, on définit dans Géogébra les suites
ak=Séquence[Somme[Séquence[Elément[rk, l + 1] (dθ (1 - sgn(k)) + sin(k (2 l + 1) dθ / 2) - sin(k (2 l - 1) dθ / 2)), l, 0, n - 1]] / (π (2 (1 - sgn(k)) + k)), k, 0, 31]
bk=Séquence[Somme[Séquence[Elément[rk, l + 1] (-cos(k (2 l + 1) dθ / 2) + cos(k (2 l - 1) dθ / 2)), l, 0, n - 1]] / (π k), k, 1, 30]où $r_\ell$=Elément[rk, l+1] correspond à $\theta_\ell=\ell\,d\theta$.
On construit ensuite les fonctions $a_k\,cos(k\,x)+b_k\,sin(k\,x)$ correspondantes, précédées de la fonction constante $a_0$, jusqu’à un curseur entier m, par
fk=Insérer[Fonction[Elément[ak, 1], 0, 2*pi], Séquence[Elément[ak, k + 1] cos(k x) + Elément[bk, k] sin(k x), k, 1, m], 1]Finalement, la fonction r=Somme[fk] (dont on cache le graphe mais dont on affiche le texte "r(x)="+r quelque part) est celle qu’on utilise dans a=Courbe[r(t)*cos(t), r(t)*sin(t), t, 0, 2*pi]

- Une courbe polaire définie par des points


Commentaires