Permutations
On utilise CaRMetal pour programmer en JavaScript sur les permutations et pour visualiser les résultats.
Le langage javascript, dans son utilisation courante est semblable pour sa syntaxe de base à java ou C/C++ : accolade, points-virgule, boucles for et while. La grosse différence c’est que javascript est très souple sur les types et le nombre d’arguments dans les fonctions.
CaRMétal permet d’écrire très rapidement un programme en javascript et sans compilation ou autres complications, d’en visualiser le résultat. Il permet également de faire interagir la partie géométrie interactive et programmation, ce que nous n’utiliserons quasiment pas ici, nous bornant à visualiser les résultats sous formes de formules LaTeX ou de graphe avec les fonctions spéciales CaRMétal de Point, de Segment et de formules.
Par exemple :
for(var i=1; i<k; i++)
Segment(Point(i,-h),Point(i,-(h+1)));fait une série de segments verticaux entre les points de coordonnées (i,-h) et (i, -(h+1)).
Les algorithmes dans le fichier joint permettent de créer une permutation au hasard, d’afficher une permutation sous la forme usuelle, de composer des permutations, d’exponentier une permutation, de construire l’orbite d’un élément, de décomposer une permutation en cycles disjoints, de calculer l’ordre d’une permutation (ppcm des longueurs de ses cycles), de décomposer une permutation en produits de transpositions, de transpositions élémentaires, d’afficher ce produit sous forme graphique, de manipuler l’ordre lexicographique.
Une application intéressante des permutations est dans l’action de $\mathfrak{S}_4$ sur le cube et sur le tétraèdre, comme décrit dans cette superbe page d’Alain Busser (prenez vos lunettes 3D). Mais une telle application me parait trop ambitieuse à programmer. J’essaierai d’en faire une version Geospace en tentant d’y mettre moins de 15 minutes, ce qui est le temps maximum que je vous conseille de consacrer à une illustration à l’aide d’un logiciel.
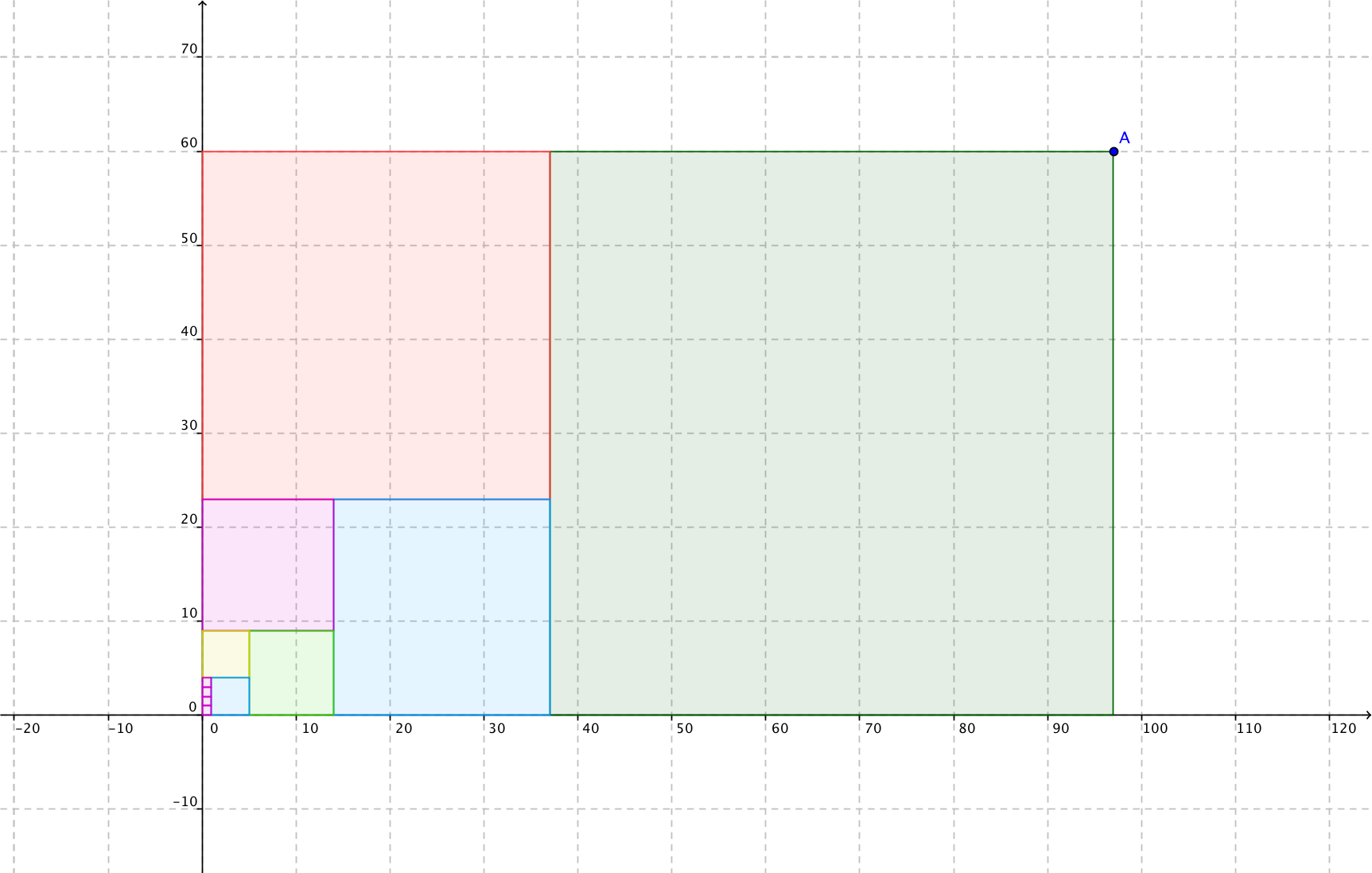
PGCD et anthyphérèse
Nous utilisons le tableur de Géogébra pour décomposer un rectangle de côtés pxq en carrés par soustractions itérées. La taille du dernier carré donne le Plus Grand Commun Diviseur de p et q. Avec un peu d’entraînement, cette construction se fait en moins de dix minutes.
Remarquez qu’en n’arrêtant pas aux nombres entiers, on retrouve la décomposition en fractions continues du rapport p/q par la suite des nombres de carrés qui apparaissent.
Attention que la version de geogebra accessible à l’oral n’est pas a priori la version 4 mais la version 3.2 !



Commentaires