Dans la séance du 14 décembre, vous avez dû trouver les points critiques d’une fonction de $\mathbb{R}^2$ dans $\mathbb{R}$ ; déterminer la nature de ces points critiques (max, min, point selle). xcas peut vous aider à automatiser ces tâches et visualiser les résultats pour articuler le registre algébrique et le registre graphique.
La question concerne $f(x,y)=x^4 +y^4 −2x^2 +4xy−2y^2$. On entre cette fonction avec une affectation := On la visualise avec densityplot
plotdensity(f(x,y),[x=-2..2,y=-2..2],xstep=0.05,ystep=0.05)
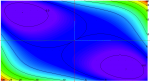 On voit clairement le point selle en (0,0) et deux minima.
On la dérive avec diff :
On voit clairement le point selle en (0,0) et deux minima.
On la dérive avec diff :
df:=diff(f(x,y),[x,y])On cherche ses points critiques avec solve :
s:=solve(df,[x,y]) Attention, ici seules les solutions réelles nous intéressent !
rs := select(x->(im(x[0])==0),s)On vérifie que la différentielle y est bien nulle :
for( j:=0; j< size(rs); j++) {
afficher(rs[j]+":"+evalf(subst(df,[x,y],rs[j])[0]));
}On place ces points sur le graphique :
for( j:=0; j< size(rs); j++) {
point(rs[j]);
}On trouve le type des points critiques en calculant la hessienne formelle avec diff :
ddf := simplify(diff(df,[x,y]))On est intéressé par la hessienne numérique à chacun des points critiques :
for( j:=0; j< size(rs); j++) {
h[j]:=simplify(subst(ddf,[x,y],rs[j]))
}On en étudie la forme quadratique associée :
for( j:=0; j< size(rs); j++) {
q[j]:=([x,y]*h[j]*[[x],[y]])[0]
}La forme de Gauss de chacune nous donne la signature et donc le type de point critique : max si (-,-), selle si (+,-) et min si (+,+).
for( j:=0; j< size(rs); j++) {
afficher(rs[j]+": "+(gauss(q[j],[x,y])))
}qui confirme bien ce que nous avons observé graphiquement.


Commentaires (fermé)