Nous visualisons les tables de multiplication et d’exponentiation dans $\mathbb{Z}/n\mathbb{Z}$ à l’aide de Géogébra.
On choisit un entier n (par un curseur entier), et on visualise $\mathbb{Z}/n\mathbb{Z}$ comme une séquence de points sur le cercle unité :
z=exp(2*i*pi/n)
C=Cercle[(0,0),1]
O=(1,0)
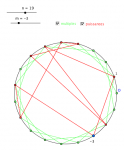
zk=Séquence[z^k,k,2,n-1]On choisit une classe m (curseur entier) et on visualise ses multiples comme une étoile, un polygone non convexe :
zm = z^m
zkm=Séquence[z^(k*m),k,1,n]
Séquence[Segment[Elément[zkm,k],Elément[zkm,k+1]],k,1,n-1]Si ce polygone passe par 1, m et n sont premiers entre eux, sinon, m est un diviseur de zéro. Quand n est premier, toutes les classes non nulles sont inversibles. On visualise la table de multiplication :
Tableau[Séquence[Séquence[Reste[j*k, n], k, 0, n - 1], j, 0, n - 1]]On regarde ensuite les puissances de m :
zmk=Séquence[z^(Reste[m^k,n]),k,1,n]
Séquence[Segment[Elément[zmk,k],Elément[zmk,k+1]],k,1,n-1]On visualise la table des puissances :
Tableau[Séquence[Séquence[Reste[j^k, n], k, 0, n - 1], j, 1, n - 1]]L’ordre de l’élément divise l’ordre du groupe (n-1) et on a donc $m^{n-1}\equiv 1[n]$ quand $n$ est premier, c’est le petit théorème de Fermat.
On ne peut malheureusement pas aller très loin avec cette méthode naïve, on aboutit à des "non défini" assez rapidement, $12^14$ par exemple est un entier à plus de 16 chiffres et ne peut pas être utilisé pour ce genre d’arithmétique. Il faut alors recourir au tableur :
Après avoir initialisé la première ligne et la première colonne par des entiers croissants, on colle comme expression :
B2=Reste[A2 $A2, n]qu’on étend à tout le tableau. Ainsi, dans la ligne m, la kième case est le produit de la première colonne (m) par la case précédente à gauche ($m^{k-1}$), modulo n, ce qui garantit le non dépassement. On observe que, pour n premier, la colonne n-1 est bien remplie de 1, sauf aux lignes d’indices multiples de n.
La figure se trouve sur i2geo.
Test de primalité de Miller-Rabin
Remarquez bien, dans la construction précédente, dans la table des puissances, la dernière colonne, qui n’est composée que de 1 si $n$ est premier et qui est beaucoup plus complexe quand $n$ est composé. Cette condition nécessaire pour que $n$ soit premier constitue un test de primalité de $n$. Beaucoup moins coûteux est le test de primalité de Miller-Rabin : pour $n$ un grand nombre premier, $n-1$ est pair et s’écrit $n-1=2^r\times d$ avec $d$ impair. Pour que $m^{n-1}\equiv 1[n]$, il faut nécessairement que soit $m^d\equiv 1[n]$ soit qu’il existe un entier $\ell
Il est très simple d’implémenter ce test avec xcas :
MR(n):={// Test de primalité de Miller-Rabin
local (d:=n-1), (s:=0), a, r, j;
while((d mod 2)==0){ s:=s+1; d:= d/2; }
// a = 2^s*d, d impair
for( j:=2; j<11; j++) { // 2(log n)^2
a := j; // hasard n;
a := powmod(a, d, n); r:=0;
if(a<>1) {
while((((a+1)mod n)!=0) and (r<s)){ // a = -1 mod n?
a:=powmod(a,2,n); r:=r+1; // a = 2^r*d, r<s
}
}
if (((a mod n)!=0) and (r==s)) return faux; //N'est pas premier
}; // Si a réussi 10 fois
return vrai; // Probablement premier
}
:;Et on peut constater que c’est très rapide et conforme à un test non probabiliste de primalité :
for j from 10001 to 20000 by 2 do if(MR(j)!=isprime(j)) afficher(i+MR(j)+isprime(j)); end_do

Commentaires