Énoncé du problème
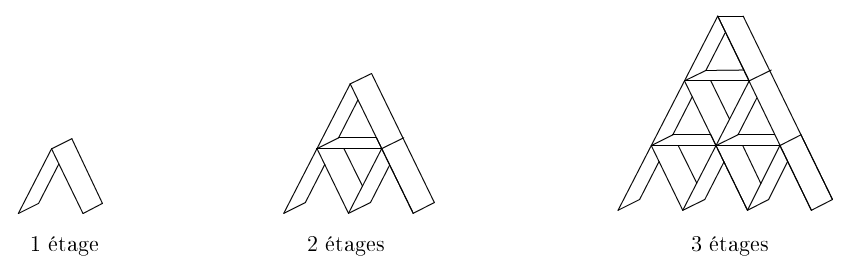
Un château de cartes à un étage est composé de deux cartes.
Un château de cartes à deux étages est composé de sept cartes.
Pour réaliser trois étages, il faut quinze cartes.
Combien faut-il de cartes pour réaliser un château de sept étages ? Trente étages ? Cent étages ?
Choix du problème
Un sujet simple à comprendre et pour lequel les élèves peuvent se lancer facilement dans la recherche : ils peuvent faire des dessins pour comprendre le mécanisme de construction des châteaux et déterminer rapidement le nombre de cartes nécessaires pour obtenir des
châteaux ayant un petit nombre d'étages.
Compétences transversales
♦ Mettre en place une stratégie pour compter le nombre de cartes.
♦ Organiser sa recherche, ses idées de manière claire.
♦ Transmettre sous forme de textes, schémas, figures, codages. . .sa démarche de recherche à une personne extérieure.
♦ Être capable de raisonner avec logique et rigueur et donc savoir :
– Identifier un problème et mettre au point une démarche de résolution
– Identifier, expliquer, rectifier une erreur
– Distinguer ce dont on est sûr de ce qu'il faut prouver
– Mettre à l'essai plusieurs pistes de solution
♦ Communiquer, à l'écrit, en utilisant un langage mathématique adapté
Connaissances mathématiques
♦ Utilisation éventuelle de la notion de suite.
♦ Utilisation de la formule permettant de calculer la somme des n premiers entiers :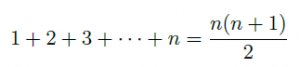
♦ Ce sujet peut être traité sans faire appel à des aspects du programme de mathématiques du collège ce qui peut avoir comme objectif d'intéresser des élèves plutôt décrocheurs face aux mathématiques.
Solution possible
Pour un château à n étages :
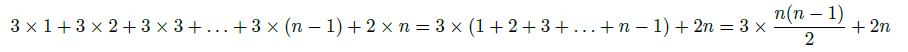
Ici, on compte les cartes 3 par 3 sur chaque étage et on ajoute les cartes de la base.
Retours d'expériences
Des retours d'expériences partagés par les enseignant.e.s du groupe d'expérimentation qui ont mis en place le problème qui déchire dans le cadre d'un enseignement fondé sur les problèmes
