
Nous proposons une organisation pour fonder son enseignement sur des problèmes (notamment des situations didactiques de recherche de problèmes) et les intégrer dans la classe ordinaire
Organisation
Pour mettre en œuvre cette progression particulière, il faut tenir compte de plusieurs éléments :
1. La progression commune de l’établissement. Il est fréquent que les équipes de mathématiques travaillent autour d'une progression commune sur chaque niveau de classe. De même un ou plusieurs devoirs communs ou examen blancs viennent ponctuer l'année. Il est donc nécessaire que la progression annuelle qui intègre les SDRP ou autres problèmes soit le plus en adéquation avec cette progression commune.
2. Les problèmes choisis ne permettent pas d’atteindre toutes les notions du programme fixée pour un niveau de classe.
Pour chaque problème choisi, nous avons recensé les notions mathématiques du programme potentiellement travaillées. Les savoirs et savoir-faire qui ne sont pas atteints sont traités dans une séquence « traditionnelle » intégrée à la progression ou sont traités en rituel (au début de chaque heure) en parallèle de la séquence principale.
Cette articulation entre ces trois types de séquences (axées autour d’un problème, « traditionnelles » ou en rituel de début d’heure) permet de couvrir l’ensemble du programme, de travailler les dimensions sémantiques et syntaxiques et de proposer des séquences avec une activité mathématique diversifiée.
3. La partie rituelle de début d’heure permet également de traiter en majeure partie l’acquisition de techniques. On évite ainsi des séances axées uniquement sur le travail technique (où la dimension syntaxique est privilégiée). Ces séances, mêlant travail de techniques en rituel et phase de recherche de problème, seront alors plus diversifiées.
Mise en œuvre d'une séquence "problème"
Nous partons du principe que l'élève dispose d'au moins deux supports : un pour le cours et un pour les exercices. Ces supports (cahiers, classeurs...) sont variables suivant l'établissement.
Pour mieux comprendre ce qui suit, il est important d'être familier avec les SDRP et leur mise en œuvre.
La séquence va s'organiser autour de quatre étapes importantes :
1. La recherche du problème
2. Les études
3. La synthèse
4. Le cours




DREAMaths
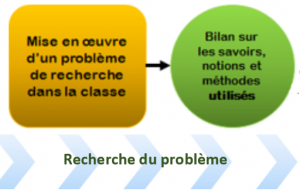
La mise en œuvre donne lieu à un bilan de la recherche qui servira de base pour approfondir l'étude du problème et organiser la suite de la séquence. Le bilan de la recherche contient habituellement :
♦ Les conjectures ou propriétés proposées par les élèves (en distinguant ce qui a été démontré du reste)
♦ Les raisonnements et méthodes utilisés
♦ Les savoirs mathématiques évoqués
♦ Les difficultés rencontrées
Ce travail peut se faire sur le support d'exercices. Le bilan de la recherche doit être mis en évidence (en couleur)
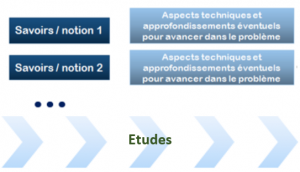
Il faut compter en général plusieurs heures
Ce sont les paragraphes qui vont structurer votre séquence et permettre d'approfondir le travail qui a été commencé en classe pour permettre aux élèves d'avancer dans la résolution du problème et de travailler les notions mathématiques ciblées. Elles s'articulent autour :
♦ Des retours sur les différents points évoqués dans le bilan (justification, approfondissement…)
♦ De ce qu’il reste à investiguer
♦ Des connaissances mobilisées
Ces études comportent :
♦ des points cours bien identifiables
♦ des exercices en lien direct avec la situation ou avec les connaissances mobilisées
Ce travail se fait sur le support d'exercices. Les points cours sont à mettre en évidence dans le cahier (en couleur) pour que l'élève puisse y faire référence au fur et à mesure que l'on avance dans la séquence
Il s'agit de faire un résumé de la séquence pour rappeler aux élèves le "parcours" effectué et les notions mathématiques abordées
Cette synthèse peut se faire sous forme de carte mentale avec comme point de départ le problème en lui-même. Elle est à coller à la fin de la séquence dans le support d'exercices

Ce sont les traces écrites plus formelles, organisées sous forme de fiches méthodes ou chapitres, pour que l'élève puisse avoir un support rigoureux des notions qui ont été bordées.
Pour gagner du temps, les traces écrites sont photocopiées et distribuées aux élèves. Elles sont stockées dans le support de cours.
