L'énoncé de la situation
On considère un billard de forme rectangulaire qui est quadrillé de façon régulière (c’est-à-dire qu’il a un nombre entier de lignes et un nombre entier de colonnes).
Aux 4 sommets du billard il y a une ouverture qui permet d’envoyer un rayon lumineux le long des diagonales du quadrillage.
Le rayon lumineux « rebondit » sur les côtés du rectangle et ne peut sortir du billard que s’il arrive sur un des 4 sommets
Question
Existe-t-il un moyen de déterminer à l’avance le nombre de carreaux traversés par le rayon lumineux dans le billard en fonction de ses dimensions?
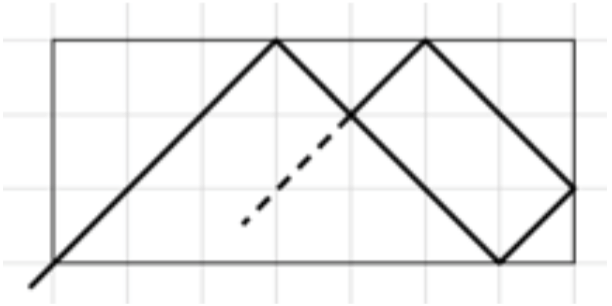
Un exemple
Les mathématiques en jeu
- Notions de multiples et de diviseurs
- Notion de nombres premiers et de nombres premiers entre eux
- Agrandir ou réduire une figure en utilisant la conservation des angles et la proportionnalité entre les longueurs de la figure initiale et celles de la figure à obtenir
- Calculer le PGCD et le PPCM de deux nombres entiers
- Calcul littéral lors des conjectures et des preuves.
Retours d'expériences
Des retours d'expériences partagés par les enseignant.e.s du groupe d'expérimentation qui ont mis en place le problème du Billard dans le cadre d'un enseignement fondé sur les problèmes