Parmi les problèmes recensés dans les pages de ce site, beaucoup peuvent être utilisés dès le début du cycle 3
Même si la plupart des analyses mathématiques de ces situations sont rédigées avec un langage et un formalisme mathématiques qui pourrait effrayer les enseignants non initiés, cela n’empêche pas la prise en main et la dévolution de ces situations par de jeunes élèves.
Les retours d'expérimentations peuvent aider à se lancer.
Des Situations Didactiques de Recherche de Problèmes (SDRP)
Le problème qui déchire est un excellent exemple de problème qui peut être utilisé dès le CM1. D'un point de vue des contenus mathématiques qui apparaissent dans la recherche en CM1, notons la notion de multiple, la division euclidienne. Voir un compte rendu dans la Newsletter 1. En CM2 et en sixième, ce problème est l'occasion de parler de parité, de division euclidienne, de reste et de quotient.

Le plus grand produit est un problème abordable en cycle 3. L'organisation des essais, la décomposition additives des nombres et la division euclidienne peuvent être abordés dans ce problème.
La difficulté d'atteindre une preuve formelle en cycle 3 peut être l'occasion de mettre en évidence un "exemple générique", c'est à dire, "l'explicitation des raisons de la validité d'une assertion par la réalisation d'opérations ou de transformations sur un objet présent non pour lui‐même, mais en tant que représentant caractéristique d'une classe d'individu" (Balacheff, 1987, page 20).
Ici, par exemple, on peut prendre l'exemple de 3 nombres consécutifs, dont l'un sera divisible par 3 et les deux autres congrus respectivement à 1 et 2.
Les régions du disque est un problème de dénombrement qui met en garde contre un raisonnement qui s'appuierait sur des exemples qui cette fois ne seraient pas "générique".
La conjecture évidente issue de premiers essais débouche sur un résultat qui s'avère faux. Là encore la preuve formelle ne sera pas un objectif à atteindre en cycle 3, en revanche, le mécanisme de preuve peut parfaitement être abordé avec des élèves de primaire sur des cas simples, par exemple avec 4 points sur le cercle (c'est la 4ème méthode de l'analyse mathématique).
Des problèmes pour chercher
Le château de cartes est un problème de pré-algébrisme où l'élève devra repéré un motif qui décrit les constructions successives.
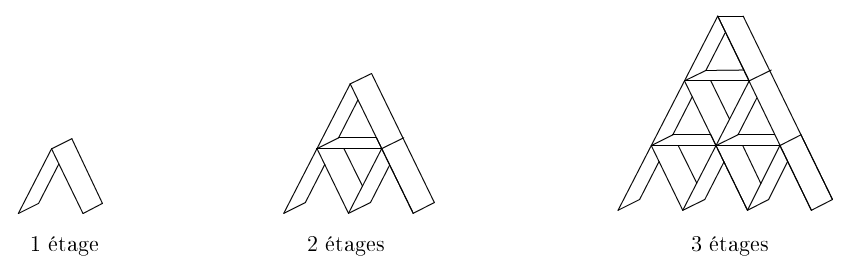
Un château de cartes à un étage est composé de deux cartes.
Un château de cartes à deux étages est composé de sept cartes.
Pour réaliser trois étages, il faut quinze cartes.
Combien faut-il de cartes pour réaliser un château de sept étages ? Trente étages ? Cent étages ?
Bien que les probabilités ne soient pas au programme du cycle 3, on visera plutôt à travers ce problème la représentation d'une situation par un arbre
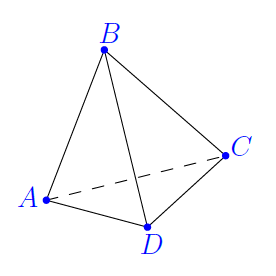
Une fourmi peut rentrer ou sortir dans un piège par le point A. Quand elle est à un sommet,
elle choisit au hasard une des trois arêtes qui passent par ce sommet. La fourmi est vivante si
elle retourne au point A en ayant parcouru au plus 4 arêtes.
Sa chance de survie est-elle supérieur ou inférieure à une chance sur deux ?
Même si le concept n'est pas manipulé en cycle 3, peut tout à fait être abordé, en expliquant que l'on va multiplier un nombre par lui-même et recommencer l'opération pour ne s'intéresser qu'au chiffre des unités du résultat. La notion de reste dans la division euclidienne apparaît naturellement.
Le chiffre des unités de 131 est 3.
Le chiffre des unités de 132 est 9.
Quel est le chiffre des unités de 133 ? de 134? ...
Ce problème mêle arithmétique et algèbre. L'objectif est de trouver une méthode efficace pour calculer, sans calculatrice, la somme de dix entiers consécutifs.
Ce problème peut être vite résolu pour les élèves mais la mise en commun peut être organisée sous forme de "battle". Cette organisation va permettre une réelle stimulation et recherche d'efficacité dans la méthode proposées par les élèves.
Trouver le plus rapidement possible la somme de 10 nombres entiers consécutifs.
Par exemple la somme de 17, 18, 19, 20, 21, 22, 23, 24, 25, 26.
Des fictions réalistes
Fuites à Fukushima est un problème de déplacement aléatoire d'un robot. Il peut mobiliser des notions assez poussées comme les suites récurrentes mais, en cycle 3, est très pertinent pour mettre en œuvre des techniques de dénombrement comme compter de grandes quantités
L'arbre est un problème de modélisation d'évolution d'un arbre. Comment va-t-il grandir ? Quelle sera sa forme ? On peut étudier ici plusieurs paramètres et les modèles d'évolutions que l'on peut choisir sont divers et variés et vont dépendre du choix de modélisation fait par les élèves.
Liaison école-collège
Un exemple de dispositif de résolution collaborative entre deux classes de cycle 3 dans le cadre d'une liaison école-collège



