Un peu d’ombre

Intérêt du problème

Ce problème est l’occasion de travailler la notion d’aire, sans recours aux formules usuelles, mais en utilisant diverses unités, ce qui conduit à différents calculs. La mise en commun des méthodes utilisées peut en être d’autant plus intéressante.

Réponse

L’aire du kiosque est 40 $m^{2}$

Démarches possibles

Première démarche  : compter combien il faudrait de kiosques pour occuper toute la place

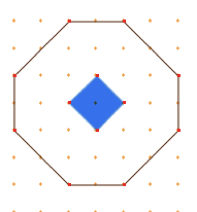
Sans découpage on peut en placer 9. Il reste autour quatre trapèzes que l’on peut découper en 20 petits triangles. Comme le kiosque est composé de 4 de ces triangles, cela en fait 5 de plus.

L’aire de la place est donc 14 fois celle du kiosque, l’aire de celui-ci est 560 $m^{2}$÷14 = 40 $m^{2}$

Deuxième démarche : prendre une unité de mesure intermédiaire.

Le kiosque est composé de quatre petits triangles, que l’on peut assembler en deux petits carrés, ou encore il est la moitié d’un plus grand carré (dans lequel il est inscrit). On cherche alors à déterminer la valeur en $m^{2}$ de cette unité de mesure intermédiaire.

Le comptage des triangles est le plus long, mais sans difficulté et il conduit à un calcul très simple : il y en a 56, donc chacun a une aire de 10 $m^{2}$.

Le comptage des carrés nécessite des regroupements de triangles. On trouve 28 petits carrés ou 7 plus grands. On peut aussi s’intéresser au grand carré entourant la place et soustraire les quatre coins. On trouve aussi 28 petits carrés (36 - 4×2) ou 7 plus grands (9-2). Un petit carré a une aire de 20 $m^{2}$ (560 :28). Le plus grand a une aire de 80 $m^{2}$ (560÷7).

Le kiosque correspond

• à deux petits carrés, soit 20 $m^{2}$×2
• à quatre triangles, soit 10 $m^{2}$×4
• à la moitié d’un plus grand carré soit 80$m^{2}$ ÷ 2.