Poly-polygones
Réponse
On peut obtenir un triangle équilatéral quand le nombre de côtés du polygone est un multiple de 3.
Démarches possibles
Les élèves vont commencer par faire des tracés et des observations sur les figures données. Lorsque le nombre de côtés des polygones augmente, les essais deviennent vite pénibles : certains préféreront raisonner.
Si la classe a l’habitude d’un logiciel de géométrie dynamique, il peut être utilisé avec profit. Par exemple, on trace un polygone à 11 côtés et un triangle équilatéral ayant un sommet commun avec ce polygone, inscrits dans un même cercle : on constate que les deux autres sommets du triangle ne coïncident pas avec des sommets du polygone.
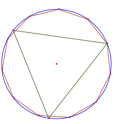 La généralisation demandée en question 2 oblige à formuler la conjecture : cela ne marche que si le nombre de côtés du polygone est multiple de 3.
Explication : deux côtés égaux du triangle correspondent à un même nombre de côtés du polygone.
La généralisation demandée en question 2 oblige à formuler la conjecture : cela ne marche que si le nombre de côtés du polygone est multiple de 3.
Explication : deux côtés égaux du triangle correspondent à un même nombre de côtés du polygone.


Commentaires