Énoncé du problème
Étant donnés quelques points placés sur une feuille, donne une méthode pour savoir combien on peut tracer de segments différents joignant deux quelconques de ces points.
Tu pourras commencer par des petits nombres de points (2 ; 3 ; 4. . . ) ensuite pour 20, pour 108 et même pour un nombre de ton choix très grand.
Variantes
On peut introduire la lettre dans l’énoncé à la place « d’un nombre de ton choix très grand » ce qui peut poser le problème du sens de la lettre en algèbre.
On peut présenter le problème avec un tableau tel que :
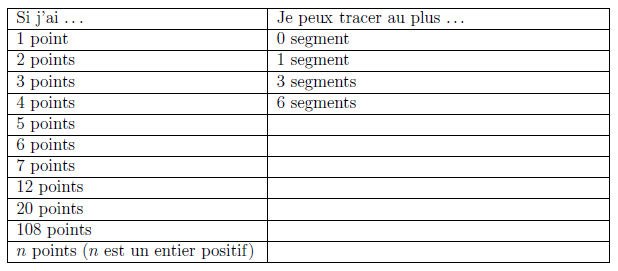Le risque avec un tel tableau est que les élèves peuvent avoir le sentiment d’avoir réalisé le travail demandé en se contentant de remplir les cases de la deuxième colonne.
Choix du problème
Compétences transversales
♦ Découvrir la recherche mathématique (utilisation de dessins, couleurs. . . )
♦ Mettre en place une technique de dénombrement : se rendre compte de l’efficacité d’un raisonnement, d’une procédure par rapport à un simple comptage « à la main »
Connaissances mathématiques
♦ C’est un premier sujet dont la consigne est simple : les élèves peuvent se plonger facilement dans la recherche sans être bloqués.
♦ Le sujet ne fait appel à aucun point du programme de 4ème : cet exercice crée un changement
avec les exercices auxquels sont habitués les élèves et de plus ils n’ont besoin d’aucun contenu particulier.
♦ Il leur est possible de faire des figures simples qui ne demandent pas de technicité particulière.
♦ Ce sujet peut amener à l’élaboration d’une formule :
— par l’utilisation éventuelle de la notion de suite ;
— par l’utilisation de la formule permettant de calculer la somme des n premiers entiers :
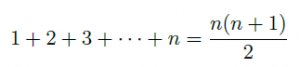
Solutions possibles
Première solution
• Pour 5 points : remarquer qu’avec le premier point on peut tracer 4 segments, avec le deuxième point on peut tracer 3 segments, avec le troisième point on peut tracer 2 segments, avec le quatrième point on peut tracer un dernier segment.
Ceci revient à additionner les nombres de 1 à 4.
• Pour n points : il faut donc additionner les nombres de 1 à n - 1 ce qui est égal à n(n - 1)/2.
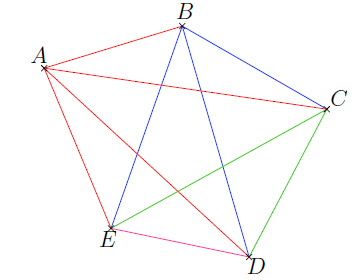
Deuxième solution
On peut résoudre ce problème en raisonnant avec les nombres : sur quelques dessins comportant peu de points on peut trouver le nombre de segments à tracer et remarquer qu’on ajoute successivement 1, 2, 3, 4 . . . au résultat précédent.
Troisième solution
On peut déterminer le nombre de segments par récurrence en remarquant qu’ajouter un point revient à ajouter un certain nombre de segments. On obtient ainsi la formule de récurrence suivante :